区块链环境下农户和合作社上链行为网络演化博弈

王旭坪 马睿泽* 阮俊虎 孙自来

(1.大连理工大学 经济管理学院,辽宁 大连 116024;2.西北农林科技大学 经济管理学院,陕西 杨凌 712100)

0 引言

农民参加合作社是我国农村经济发展的主要业态特征之一,农民专业合作社是实现小农户和大市场有效对接的重要载体,关系到农产品质量安全及农民脱贫致富进程,党和国家正在积极探索合作社的发展模式[1]。习近平总书记指出,要鼓励发展农民合作社,加强对农民的科技服务,推动农业适度规模经营,以提高农产品质量[2]。2020年7月出台的《全国乡村产业发展规划(2020-2025年)》,明确提出要以新兴技术为手段培育农产品品牌,引导农民合作社实施农产品质量安全追溯管理,推动农产品供应链质量安全追溯平台对接和信息共享①中华人民共和国农业农村部:http://www.moa.gov.cn/govpublic/XZQYJ/202007/t20200716_6348795.htm。区块链技术是完成这一目标的重要技术手段。2020年4月农业农村部颁布的《数字农业农村发展规划(2019—2025年)》指出“推动区块链技术在农业生产决策和管理智能化中的创新应用”②中华人民共和国农业农村部:http://www.moa.gov.cn/nybgb/2020/202002/202004/t20200414_6341532.htm。同年6月吉林省半顷田种植专业合作社便搭建起“农机物联网+区块链”信息平台,有效提升了合作社的服务能力和运营效率③长春市人民政府:http://www.changchun.gov.cn/zw_33994/yw/zwdt_74/jjdt/202006/t20200601_2361515.html。可见,对区块链在农民专业合作社中应用的研究具有重要现实意义。

国内外学者已经对农户和合作社之间的关系进行了不少研究,得出以下结论。首先,合作社可以满足农户应对市场的需要[3],如袁雪霈等发现合作社能够通过测算农产品市场需求量、科学管控农户生产过程和生产规模、保证农产品质量、与企业议价等措施防止农产品市场价格的剧烈波动,以达到社员收入稳定的目的[4]。其次,合作社可以降低农户的生产成本[5],如侯晓康等发现合作社可以借助规模效应解决单个农户在生产投入市场中面临的高额交易成本问题[6]。再次,合作社可以增强农户的风险防范能力[7],如袁雪霈等指出合作社主导的农业一体化组织相较于分散性的小农经济组织具有独特优势,主要体现在抵御自然和市场风险能力方面[8]。不难看出,农户和合作社之间存在双向委托代理关系[9],一方面,合作社作为农户的代理人进行市场营销、统一生产技术、防范市场风险、构建农产品品牌等[10]。另一方面,农户作为合作社的代理人保证农产品品质、不违规使用农药和化肥等[11]。然而,农户和合作社之间信息的不对称性导致了道德风险和逆向选择问题,使两者之间出现了严重的信任危机,进一步导致了我国“空壳合作社”现象的出现[1]。而区块链技术为解决这一难题提供了新契机。区块链是一个分布式的共享账本和数据库,其去中心化、开放透明、不可更改、匿名安全的技术特点可以有效解决农户和合作社间的信任危机[12]。为此,本文就区块链技术在农户和合作社中的采纳问题展开研究。

然而,区块链技术能否被农户和合作社采纳受到参与主体以及市场环境等诸多因素影响[8]。阮俊虎等指出农业领域中新技术的应用往往会对原有的农产品供应链运营模式和市场环境产生巨大变革[13]。农户和合作社在采纳区块链技术后势必会产生引进新型硬件设备、软件平台和管理人员等成本[14]。同时,农产品市场价格、农产品质量以及市场需求量也会发生明显变化[15]。另外,合作社的服务水平和服务成本也会发生相应的改变[16]。这些都是农户和合作社在判断是否采纳区块链技术时要考虑的因素。事实上,农户和合作社的区块链技术采纳决策是两者之间的博弈过程,一方的博弈策略直接影响对方的收益,如何进行收益分配以及单边不采纳而导致对方的损失也是博弈主体关心的问题[17]。

农户和合作社在博弈决策中具有有限理性,需要通过学习和模仿不断改进策略来提高收益[18]。而演化博弈论正是针对有限理性的博弈主体,结合生物进化论的思想,将博弈分析与动态演化过程相结合的分析方法[19]。陈莫凡等运用演化博弈理论构建农户和合作社的生态农业技术扩散博弈模型[20],詹国辉从演化博弈的视角探究了农户和合作社之间集体行动的演化逻辑[21],王晓莉等通过构建农户、合作社和地方政府间的演化博弈模型分析市场化生态补偿式扶贫项目的推广问题[22]。然而,现实中农户和合作社之间“多对多”的交互关系构成了一种具有拓扑统计特征的复杂网络[23]。农户和合作社的博弈策略会随着网络结构的变化而改变,本质上是以复杂网络为载体的演化博弈过程[24]。传统的演化博弈理论可以在一定意义上诠释农户和合作社的决策机制,但未能呈现博弈群体内个体的交互过程,使结论过于理想化和抽象化[1,25]。同时,区块链作为一种新兴技术在农民专业合作社领域中的应用正处于探索阶段。因此,本文将演化博弈理论与复杂网络理论相融合,构建了农户和合作社的两种群网络演化博弈模型,并检验了模型的有效性,深入探究与博弈主体和市场环境相关的因素对农户和合作社上链行为的作用机理。论文成果既可为区块链技术在农民专业合作社中的推广工作提供实践指导,又丰富了区块链技术在农业领域中推广的理论研究。

1 “农户-合作社”演化博弈模型

1.1 演化博弈问题描述

如图1所示,农户和合作社之间存在双向委托代理关系,信息流和物流在两者之间流通。在非区块链环境下的传统模式中,农户和合作社所共享的信息具有中心化属性,易篡改且可信度低,使道德风险和逆向选择问题充斥在两者间的交互过程中。在区块链环境下,平台利用程序算法自动记录农户生产农产品过程信息以及合作社的运营信息,并将信息存储在区块链节点上。此时,区块链信息的去中心化、不可篡改性、透明性以及实时性等技术优势显现。信息被赋予了区块链特性后变得高度对称,使得农户和合作社之间的委托代理关系不受道德风险和逆向选择的影响,实现了机器信任向人工信任的转变。

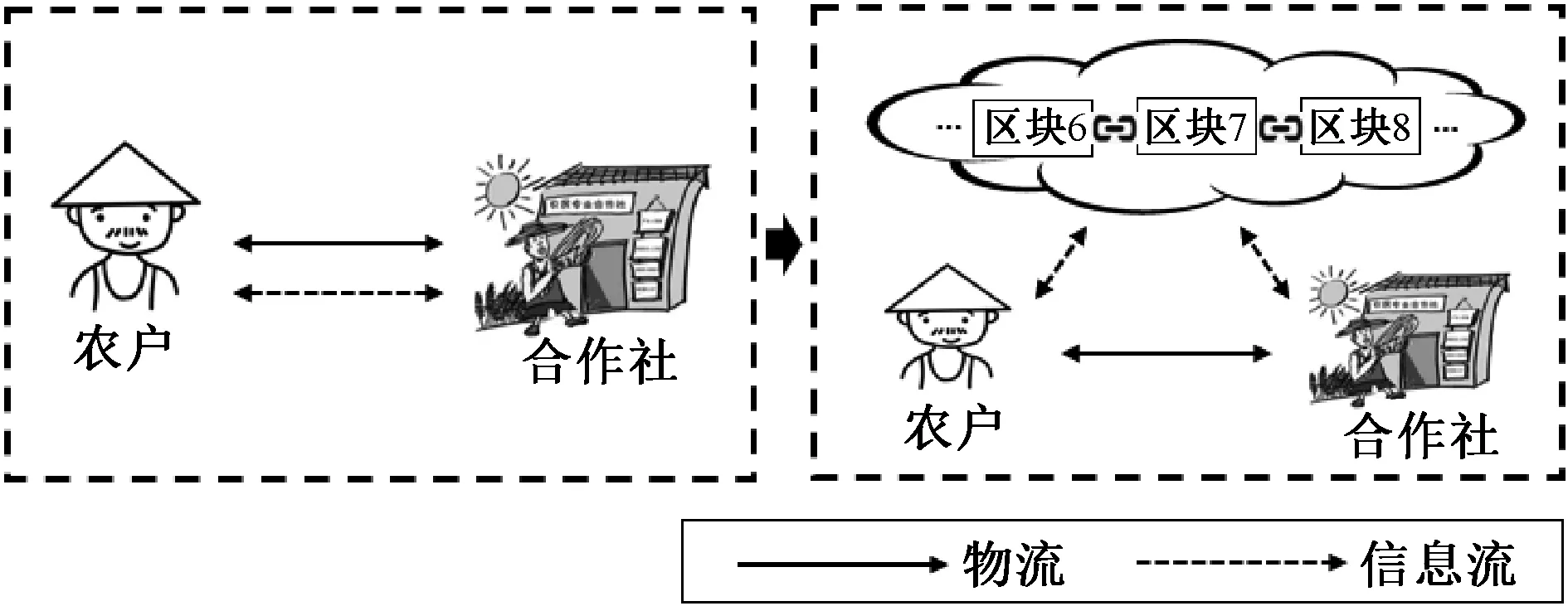
图1 采纳区块链技术前后模式图Figure 1 M odes before and after adopting the blockchain technology

农户和合作社的上链行为是两种群体之间的博弈过程,由于市场环境的不确定性,此过程是两群体在有限理性下的动态博弈过程。而演化博弈论正是针对有限理性的博弈群体,将博弈分析与动态演化过程相结合的分析方法。因此,本部分运用演化博弈论对农户和合作社上链行为的规律进行分析,找出演化博弈的演化稳定策略(Evolutionarily stable strategy,ESS)。博弈过程中,每个博弈主体根据预期收益采取“上链”与“不上链”两种策略。

1.2 模型假设

假设1在农户和合作社上链行为的博弈过程中,假设农户选择上链策略的概率为x(0≤x≤1),选择不上链策略的概率为1-x;而合作社选择上链策略的概率为y(0≤y≤1),选择不上链策略的概率为1-y。

假设2农产品价格为pi,则区块链模式和传统模式下农产品的价格分别为pB和pNB。价格敏感系数为α(0≤α≤1),代表农产品市场价格变动引起的市场需求量的变化程度。

假设3农产品质量为qi,则区块链模式和传统模式下农产品的质量分别为qB和qNB。需求质量弹性为β(0≤β≤1),代表农产品市场需求量对于产品质量变动做出反应的敏感程度。质量成本系数为γ(0≤γ≤1),表示农产品成本对质量变化反应的灵敏程度。

假设4合作社服务水平为si,则区块链模式和传统模式下合作社服务水平分别为sB和sNB。服务收益系数为θ(0≤θ≤1),代表农户从合作社提供的服务中获得效益的程度。合作社服务成本为csi,则区块链模式和传统模式下合作社服务成本分别为csB和csNB。

假设5参考Bernstein等[26]和Lee[27]的研究,假设市场需求函数是质量和价格的线性函数,成本是质量的二次指数函数。a、Di、Ci、πi分别代表市场基础需求、需求函数、成本函数、利润函数(i=B、NB)。

假设6λF和λC分别为农户和合作社的收益分配比例。根据《中华人民共和国农民专业合作社法》规定①中华人民共和国中央人民政府网站:http://www.gov.cn/xinwen/2017-12/28/content_5251064.htm,合作社须要留存部分盈余作为合作社的发展基金,故0＜λF、λC＜1,且0＜λF+λC＜1。cF和cC分别表示农户和合作社的单边上链成本,即一方采取上链策略而另一方采取不上链策略时,上链一方前期投入的沉没成本,如时间成本、机会成本等。模型参数及含义如表1所示。

1.3 博弈收益矩阵

当农户和合作社进行上链行为博弈时,不同策略组合下博弈双方的收益有所不同。在求解农户和合作社上链行为博弈的收益矩阵之前,我们需求出农产品市场的利润函数。基于Bernstein[26]等和Lee[27]等的研究成果,设定本文的市场需求函数为Di=a-αpi+βqi、成本函数为,则利润函数为

若农户和合作社都采取上链策略,即(上链,上链),则区块链技术成功实施,农户和合作社分别根据市场利润和收益比例获取收益λFπB和λCπB。同时,农户享受合作社服务的收益为θsB,合作社的服务成本为csB。同理,如果农户和合作社都采取不上链策略,即(不上链,不上链),则农户和合作社收益分别为λFπNB+θsNB和λCπNB-csNB。

若农户采取上链策略,而合作社采取不上链策略,即(上链,不上链),则区块链技术未成功实施,农户和合作社分别根据市场利润函数和收益比例获取收益λFπNB和λCπNB。同时,农户享受合作社服务的收益为θsNB,并付出单边上链成本cF,合作社的服务成本为csNB。同理,如果农户采取不上链策略,而合作社采取上链策略,即(不上链,上链),则农户和合作社的收益分别为λFπNB+θsNB和λCπNB-csNB-cC。

综上,农户和合作社的博弈收益矩阵如表2所示。

表2 博弈收益矩阵Table 2 Payoffmatrix of the game

1.4 复制动态方程

根据表2博弈收益矩阵,当农户采取上链策略时,可求出其期望收益为:

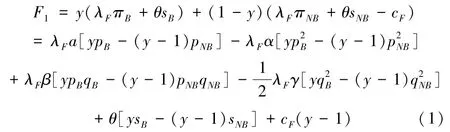
农户采取不上链策略的期望收益为:

农户分别以x和(1-x)的概率选择上链和不上链策略的平均期望收益为:

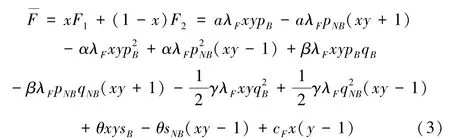
同理,合作社采取上链策略的期望收益为:

合作社采取不上链策略的期望收益为:

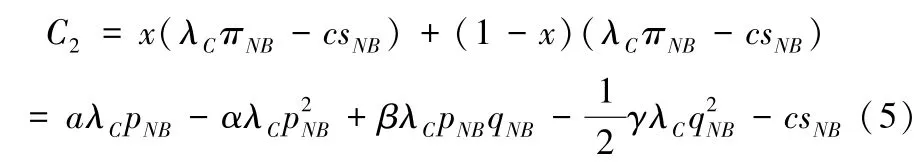
合作社分别以y和(1-y)的概率选择上链和不上链策略的平均期望收益为:

根据Malthusian动态方程[28],农户或合作社选择上链策略的增长率(dx/dt或dy/dt)等于其期望收益(F1或C1)与平均期望收益(或)的差与x或y的乘积。故农户与合作社群体的动态复制方程分别如公式(7)和(8)所示。

1.5 局部稳定性分析

根据复制动态方程(7)和(8)求出系统的雅克比矩阵:

为了分析系统均衡点的局部稳定性,根据雅克比矩阵(9)可以计算雅克比矩阵的行列式(10)和轨迹(11),分别如下:

根据雅克比矩阵的局部稳定性分析方法[29],当且仅当均衡点满足DetJ＞0和TrJ＜0时,为系统的演化稳定策略(ESS)。因此,分别将5个局部均衡点带入公式(10)和(11)中进行局部稳定性分析。其中,均衡点(x*,y*)的TrJ=0,因此均衡点(x*,y*)在[0,1]区间内始终不是系统的ESS。对模型变量间的逻辑关系进行分类讨论后,可以得出以下4种不同情境:

情境1当λFΔπ+θΔs＜0、λCΔπ-Δcs＜0时,即在实施区块链技术后,农户所得市场利润的改变量与其从合作社的服务中所获收益的改变量之和、合作社所得市场利润的改变量与其服务农户所付出成本的改变量之差都小于零时,系统的ESS为(0,0)。

情境2当λFΔπ+θΔs＜0、λCΔπ-Δcs＞0时,即在实施区块链技术后,农户所得的市场利润的改变量与其从合作社的服务中所获收益的改变量之和小于零、而合作社所得市场利润的改变量与其服务农户所付出成本的改变量之差大于零时,系统的ESS为(0,0)。

情境3当λFΔπ+θΔs＞0、λCΔπ-Δcs＜0时,即在实施区块链技术后,农户所得市场利润的改变量与其从合作社的服务中所获收益的改变量之和大于零、而合作社所得市场利润的改变量与其服务农户所付出成本的改变量之差小于零时,系统的ESS为(0,0)。

情境4当λFΔπ+θΔs＞0、λCΔπ-Δcs＞0时,即在实施区块链技术后,农户所得市场利润的改变量与其从合作社的服务中所获收益的改变量之和、合作社所得市场利润的改变量与其服务农户所付出成本的改变量之差都大于零时,系统的ESS为(1,1)或(0,0)。

可见,建立区块链机制后,农户收入的改变量与合作社服务效益的改变量之和的符号以及合作社收入的改变量与其服务成本的改变量之差的符号共同决定系统的演化稳定策略。具体分析如表3所示。

表3 均衡点分析Table 3 Analysis of equilibrium points

上述“农户-合作社”演化博弈模型诠释了农户和合作社上链行为的决策机制,但未能呈现系统内博弈主体策略的具体演化过程以及博弈群体内部的差异性,结论中的4种情境下的演化稳定策略最终收敛的状态过于极端(0或1)。然而,农户和合作社的上链行为是以个体间的协同、交互等非线性机制下开展的博弈行为,个体间的接触具有随机性和非全耦合性,且具有很强的拓扑统计特性。从本质上看,这是以复杂网络为载体的演化博弈过程,网络中个体的策略会随着网络环境以及结构的变化而改变。因此,为了解决上述博弈演化过程和结论过于抽象的问题,本文在“农户-合作社”演化博弈模型的基础上,引入复杂网络理论刻画博弈主体间的交互规律,构建农户与合作社上链行为的复杂网络上的演化博弈模型,对上述演化博弈模型进行分析与再求解,打开博弈双方策略演化的黑箱,进一步揭示博弈双方策略演化的规律。

2 复杂网络上的演化博弈模型

2.1 “农户-合作社”网络描述

随着“农户-合作社”网络中个体数量的不断增加,网络关系的建立越来越趋向随机和非全耦合,并逐渐演化为一种复杂网络。“农户-合作社”网络中通常具有聚簇性,聚簇内的农户和合作社交互频繁,聚簇之间交互较少。如陕西省黄陵县和洛川县的“苹果种植户-合作社”网络中少数节点拥有大量连接,而大部分节点有少数连接,具有严重的异质性[1,30]。网络主体倾向于与资源禀赋大的主体建立关系,即网络中度分布符合幂律分布。同时,已有研究表明社会网络具有无标度特性[31]。因此,以复杂网络为载体研究农户和合作社上链行为博弈的演化具有现实意义。

2.2 网络前提假设

基于上述对“农户-合作社”网络的结构特点和现实考虑,提出如下假设:

假设1由于农户和合作社间信息的不对称性,网络内异质性主体是有限理性的,主体选择策略的概率与策略预期收益的大小呈正相关关系,且存在决策失误而没有选择最优策略的可能。

假设2由于网络节点无法与整个网络内的所有节点建立博弈关系,“农户-合作社”网络内的节点在选择博弈对象时,将博弈范围限定在邻域内,即节点只与有连边的邻居节点进行博弈,且农户和合作社互为邻居节点。

假设3网络内所有节点采取同一策略更新规则,且节点通过比较上一轮博弈的收益和下一轮博弈的预期收益进行策略的更新。

2.3 网络演化规则

2.3.1 网络演化过程

如图2所示,本文在复杂网络理论框架下构建农户和合作社上链行为的网络演化博弈过程。博弈网络有农户和合作社两种节点;节点可以采取上链或不上链策略;节点之间的连边代表节点间的博弈关系;当连边两端的节点发生博弈时,节点根据博弈对手的策略和自身收益矩阵(表2)获得收益;各节点在每一轮演化周期与其邻域内所有节点进行一次博弈,每个节点的收益为与各邻居博弈所得收益的累加。节点在每轮演化周期结束后,以收益最大化原则判断是否进行策略更新,以与度大节点连接原则决定是否更新博弈伙伴。整个网络不断演化直到进入某个稳定的状态。

图2 “农户-合作社”网络的演化Figure 2 The evolution of “farm-cooperative”network

从“农户-合作社”网络的演化过程看,网络主体进行上链博弈的目的是实现自身收益的增值,从而使整个系统逐渐收敛到帕累托最优态。本文用系统上链率来量化博弈网络的状态,即为系统内采取上链策略主体所占的比例。

2.3.2 博弈策略更新规则

如何确定每轮演化周期博弈主体策略的更新规则是网络演化博弈的核心问题。已知博弈主体根据前一轮博弈收益来制定下一轮博弈策略,以提高收益为目的通过博弈学习不断调整策略[32]。理论上,“农户-合作社”网络节点博弈策略的更新规则包括:1)最优响应动力学[31],即假设其他节点策略不变,选择使自己收益最大化的策略;2)择优响应动力学[30],即假设其他节点策略不变,选择使自己收益有所提升的策略;3)对比较更新[33],即节点随机选择一个邻居进行收益比较,以正比于收益差值的概率模仿邻居的策略;4)模仿更新规则[34],即节点以正比于邻居节点收益的概率学习邻居的策略。

上述规则描述了网络节点如何基于已有信息更新策略,故节点所能获取的信息是设计策略更新规则的关键所在。由于农户和合作社之间信息的不对称性,网络节点不能了解博弈对手的收益函数,而对比较更新和模仿更新规则均需要博弈主体了解博弈对手的收益信息。同时,博弈主体皆以收益最大化原则做决策,择优响应动力学与此原则不符。然而,博弈主体可以根据博弈对手的历史策略以及自身收益函数制定最优策略。因此,最优响应动力学是本文博弈策略更新规则的最佳选择。

基于此,在每轮演化周期内,每个节点在假定邻居节点博弈策略不变的情况下,根据邻居上一轮的策略进行策略反思。即节点先采取自身策略的反策略,根据收益函数做一次虚拟博弈,得到虚拟收益,再比较虚拟收益与上一轮博弈收益大小,选择收益最大的策略。同时,考虑到博弈主体的有

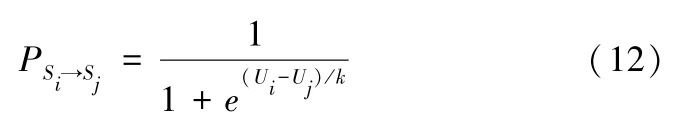
其中,Si和Sj分别为网络主体前一轮的博弈策略和本轮将更新的策略,Ui和Uj分别为网络主体前一轮博弈收益和本轮虚拟收益。k表示系统噪声(k＞0),若k趋于无限大,表示环境扰动对网络主体策略更新的影响极其严重;反之,若k趋于0,表示环境扰动对网络主体策略更新的影响非常小。

2.3.3 断边重连规则

根据复杂网络理论,在农户和合作社的上链行为博弈网络演化过程中,各节点以概率P完成策略更新后,将以概率ω随机地与网络中的其他节点进行重连。节点倾向于与资源禀赋大的节点建立合作关系,即网络的无标度特性。因此,度大的节点被连接的概率大,度小的节点被连接的概率小[36]。同时,由于节点对博弈对象的选择具有有限理性,本文以随机效用理论作为网络断边重连行为的理论基础[37],利用带有偏好的重连机制并参考文献[36]确定出连接节点i的出连概率ω为:限理性和网络的异质性对博弈策略更新的影响,企业以一定概率在下一轮博弈中采取最优响应策略,这一概率用费米函数表示[35]:

其中,D表示节点的度,j表示被连节点,G表示网络节点的集合,ε表示偏好倾向,当ε=0时,代表网络节点连接无偏好倾向,ε越大偏好倾向越明显。

“农户-合作社”网络中所有节点按照上述演化规则进行策略调整,随着时间的推进,策略分布将逐渐收敛于稳定状态,从而实现系统的帕累托最优。

2.4 模型求解算法

根据上述“农户-合作社”网络的演化规则中最优响应动力学、费米函数以及随机效用理论,设计复杂网络上的演化博弈模型的求解算法:

步骤1初始化一个存在农户和合作社两种群体的网络;

步骤2将博弈策略随机分配给网络中的节点;

步骤3进行一轮博弈;

步骤4在每轮博弈周期内,网络中的节点可以获取邻居节点的策略信息,并根据自身策略和博弈收益函数进行策略更新,若改变策略后的虚拟收益大于或等于上一轮的博弈收益,则在下一轮博弈中以概率PSi→Sj(式12)更新策略,否则策略不变;

步骤5根据网络中节点所具有的偏好机制,网络节点以概率ωij(式13)与其他节点断边重连;

步骤6转入步骤3,直至系统达到稳定状态结束。

3 模型检验与数值实验

3.1 案例分析与参数设置

黑龙江北大荒集团是我国现代化大农业的代表,土地面积为1296万亩,有“中国粮食第一产能”之称,主要从事土地发包经营、水稻等粮食作物的生产和销售①北大荒集团官方网站:https://www.chinabdh.com/。然而,包括合作社在内的农产品供应链各节点信息的不对称导致的农户违规使用农药和化肥、农产品产地造假、用陈化粮进行产品互混等食品安全和品牌危机等问题困扰着北大荒集团。为此,北大荒集团于2017年与中南建设集团合资成立了善粮味道农业科技公司。善粮味道致力于用区块链技术建立去中心化、农业价值可信的互联网平台,依托北大荒集团的优质土地研发了全球首个农业区块链数字共享服务平台,平台穿透了种植前、中、后的运营管理体系,整合了包括合作社在内的现有农业供应链,重塑了北大荒特色农产品品牌。善良味道以“物联网+区块链”为基础的智能终端,覆盖了农产品“耕-种-管-收-储-运-销”生命周期的各个环节,实现农业供应链全过程数字化和信息实时化。平台将核心数据上链,上链信息无从篡改,提升了农产品供应链各环节的运营效率。消费者通过扫码就可以查看粮食生命周期的各环节,平台架起了北大荒集团与消费者之间的信任桥梁,为消费者提供安全可信的优质农产品。北大荒集团的稻花香大米在京东商城原价32.8元/千克,采用区块链技术后价格为38元/千克②京东商城官方网站:https://item.jd.com/48240445001.htm l。

本文依托上述案例,在咨询了管理科学及复杂网络相关领域的专家后,根据本文假设和企业实际情况参考文献[38-41]对博弈模型算例设定的规则,对本文相关参数进行初始赋值,借此分析价格敏感系数(α)、需求质量弹性(β)、质量成本系数(γ)以及服务收益系数(θ)对农户和合作社上链行为的影响规律。其中,市场基础需求a=100;农产品价格pB=38、pNB=32.8;产品质量qB=60、qNB=35;合作社服务水平sB=25、sNB=15(B为区块链环境、NB为非区块链环境,下同);根据《中华人民共和国农民专业合作社法》中对合作社盈余分配的规定③中华人民共和国中央人民政府网站:http://www.gov.cn/xinwen/2017-12/28/content_5251064.htm,收益分配比例λF=0.5、λC=0.4;单边上链成本cF=5、cC=10(F为农户、C为合作社)。以“农户-合作社”网络为载体,参考文献[35]令网络偏好倾向ε=1,运用MATLAB模拟网络中博弈策略的动态演化过程。根据2016年《黑龙江省人民政府第三次全国农业普查主要数据公报》所统计的数据,农业生产经营或服务为主的农民合作社与农业经营户的数量比例1:33.6④黑龙江省人民政府网站:https://www.hlj.gov.cn/zwfb/system/2017/12/28/010858216.shtm l,将网络中合作社节点数设置为10、农户节点数为336。再根据1.5节的局部稳定性分析结论,设置α、β、γ、θ和合作社服务成本(csi)的取值,如表4所示。

表4 不同情境下的参数设置Table 4 Notation setting in different situations

3.2 模型检验

不同情境下复杂网络上的演化博弈模型(EGM-CN)的系统策略演化轨迹如图3所示。其中,纵坐标表示系统上链率;横坐标表示网络演化周期(下同)。将此结论与演化博弈模型(EGM)的局部稳定性分析结论(表3)进行对比分析,可以检验EGM-CN的正确性和参数设置的合理性。

图3 不同情境下系统策略的演化轨迹Figure 3 Evolution of strategy in different situations

如图3,当α、β、γ、θ、csi间关系满足情境 1～3 时,系统的上链率收敛于0,即系统内的主体都倾向于采取不上链策略,此结论与EGM的局部稳定性分析结论(0,0)相符。当变量间关系满足情境4时,理论上系统的ESS有(1,1)和(0,0)两种可能。就本文算例而言,情境4的实验结果只呈现出(1,1)这一种情况,故系统的上链率收敛于1。此结论与EGM的局部稳定性分析结论相符。综上,图3中不同情境下数值实验的结果与EGM局部稳定性分析结论相吻合(如表5所示)。因此,本文所构建的农户和合作社的复杂网络上的演化博弈模型正确可信,且所用算例合理有效。

表5 模型结论对比分析Table 5 Com parative analysis ofmodels

由于情境4的ESS存在(0,0)或(1,1)两种可能,为了有效分析α、β、γ、θ对系统主体上链行为策略的影响规律,依托情境4运用控制变量思想进行数值实验。同时为了保证结果的一般性,对每组参数进行100次测试,用系统上链率的平均值研究博弈网络的演化规律。

3.3 数值实验

3.3.1 价格敏感系数α对网络演化的影响

图4是在其他参数不变的情况下,农产品市场需求量对价格的敏感程度(α)的变化对网络演化影响的数值实验结果。图4(b)的横坐标表示影响因素的取值,纵坐标表示影响因素在不同取值下各演化周期上链率的平均值(下同)。如图4(a)所示,随着α的增加,“农户-合作社”网络的上链率先收敛于1或近似于1的常数,即α=0时上链率收敛于0.9788、α=0.2、0.6、0.8时上链率收敛于1、α=0.4时上链率收敛于0.9988。而当α增加到0.8到1之间的某一临界值后,网络上链率开始收敛于0。

图4 α对网络演化的影响Figure 4 Influence ofαon network evolution

值得注意的是,当α=0、0.4时上链率收敛于0到1之间的某一常数,表明本文所建立的“农户-合作社”上链行为网络演化博弈模型比传统的演化博弈模型更能反映系统内主体的差异性,所得结果也更符合实际(下同)。

由图4(b)可知,当α∈[0,0.8]时,系统上链率在[0.9,1]内小幅波动。当α取值较大时,即α∈[0.8,1],系统上链率断崖式下降到常数0.0154。这一结果表明:当农产品的市场需求对价格的敏感程度较小时,采纳区块链技术导致的农产品价格增长不会使市场需求大幅度降低,农户和合作社都倾向于采取上链行为;当价格敏感系数达到一定高度时,采纳区块链技术的农产品因价格的增加使市场需求量严重降低,“农户-合作社”网络内出现了放弃采取上链行为的主体。此时,由于网络内各主体博弈学习机制产生的羊群效应,以及产品市场需求大幅降低的双重压力,系统上链率呈断崖式下降。因此,随着价格敏感系数的增加,农户和合作社采取上链行为的意愿先小幅波动,当价格敏感系数较高时意愿呈断崖式下降。

3.3.2 需求质量弹性β对网络演化的影响

图5是在其他参数不变的情况下,农产品市场需求量对其质量变化反应的灵敏程度(β)的变化对网络演化影响的数值实验结果。如图5(a),随着β的增加,系统的上链率逐渐从收敛于0向收敛于1转变。当β=0、0.2时,上链率收敛于0。β的临界值在0.2到0.4之间,当β大于此临界值时,如β=0.4、1上链率收敛于1;β=0.6、0.8上链率分别收敛于常数 0.9428、0.9657。

图5 β对网络演化的影响Figure 5 Influence ofβon network evolution

由图5(b)可知,当β∈[0,0.2]时,系统上链率在常数0.1附近小幅波动,即农户和合作社都倾向于不采取上链行为。随着β的增加,当β∈[0.2,0.4]时,系统上链率呈指数式增长。这是因为当农产品市场需求受农产品质量影响程度很低时,农户和合作社没必要采纳新技术提升农产品质量。随着农产品市场需求受农产品质量影响程度的增加,农户和合作社采取区块链技术可通过提升农产品质量而大幅度增加市场需求,系统内主体受到市场收益增加以及系统内羊群效应的双重驱动,使系统上链率呈指数式增加。然而,由于农产品质量对市场需求的提高存在边际效用递减规律,当β增加到某一临界值时,即β∈[0.4,1]时,系统上链率在区间[0.78,0.95]增长速率变缓并小幅震荡。因此,农户和合作社上链行为的意愿随着需求质量弹性的增加先小幅波动,再呈指数式增加,最后转为缓慢增加。

3.3.3 质量成本系数γ对网络演化的影响

图6是在其他参数不变的情况下,农产品成本对质量变化反应的灵敏程度(γ)的变化对网络演化影响的数值实验结果。 如图6(a),随着γ的增加,当γ=0、0.2、0.4、0.6、0.8时,系统上链率分别收敛于常数 0.9801、1、0.9885、0.9685、0.9857。当γ达到[0.8,1]间某一临界值后,网络上链率收敛于0(如γ=1)。

图6 γ对网络演化的影响Figure 6 Influence ofγon network evolution

由图6(b)可知,当γ∈[0,0.8]时,系统上链率在(0.88,1)内小幅度波动。当γ∈[0.8,1]时,系统上链率呈断崖式降低,降低至0.0031。这是因为在区块链环境下,当提升农产品质量所需要付出的成本较低时,农产品质量提升导致的市场收益的增加可以弥补产品质量提升所产生的成本,农户和合作社采纳区块链技术的意愿较高且不易被动摇;当农产品质量提升所需要付出的成本较高时,系统内主体采取上链策略后的成本大于收益,同时受到系统内羊群效应的影响,系统上链率呈断崖式下降。因此,随着质量成本系数的增加,农户和合作社的上链意愿先小幅度波动,当质量成本系数较高时意愿呈断崖式下降。

3.3.4 服务收益系数θ对网络演化的影响

图7是在其他参数不变的情况下,农户从合作社提供的服务中获得效益的程度(θ)的变化对网络演化影响的数值实验结果。 如图7(a),当θ=0、0.2、0.4、0.6、0.8、1 时,系统上链率分别收敛于常数 1、0.9942、0.9971、0.9885、0.9971、0.9828。

图7 θ对网络演化的影响Figure 7 Influence ofθon network evolution

由图7(b)可知,随着θ逐渐增加,系统上链率在(0.899,0.975)内小幅度波动,即系统上链率变化不显著。这是因为在区块链的去中心化,公开透明以及不可篡改等技术特性下,农户和合作社之间的运营机制由人工信任转变为机器信任,实现了去信任化。在农户和合作社完全信任的情境下,农户从合作社的服务中获取收益的程度对两者采纳区块链技术的意愿影响不大。因此,无论服务收益系数如何变化,农户和合作社始终愿意采纳区块链技术,即服务收益系数对农户和合作社的上链愿意无显著影响。

4 结论与建议

农户和合作社间的信任问题一直制约着我国农民专业合作社的发展,而区块链作为一种去中心化、开放透明、不可更改、匿名安全的新型数据存储方式,为解决农户和合作社间的信任问题带来了曙光。一项新技术出现最亟待解决的问题之一便是各参与方的采纳问题。首先,本文建立了农户和合作社的上链行为演化博弈模型。演化博弈理论解释了博弈主体的决策机制,但未考虑群体网络内的拓扑特征和个体异质性。为此,本文为了得到更加精确的结论,将演化博弈理论与复杂网络理论相融合,构建了农户和合作社两种群网络演化博弈模型。从市场环境和主体交互角度提出了影响博弈主体上链行为的因素,并揭示各因素对博弈主体策略选择的影响机理。研究发现:1)在实施区块链技术后,农户所分得的市场收入的变化与其从合作社获得服务效益的变化之和的正负,以及合作社所分得的市场收入的变化与其服务社员所付出的成本的变化之差的正负共同决定了系统的均衡解;2)当农产品市场需求对价格的敏感程度α和农产品成本对质量提升的灵敏程度γ较高时,博弈主体上链意愿呈断崖式下降;3)博弈主体上链意愿随着农产品市场需求对产品质量的敏感程度β的增加先小幅波动,再呈指数式增加,最后转为缓慢增加;4)农户从合作社服务中获得效益的程度θ对主体上链愿意的影响不显著。

区块链在农民专业合作社中的应用目前还处于探索阶段,为此,基于本文研究结论提出如下建议。首先,科学控制区块链技术在合作社应用过程中的实施成本,在提升农产品质量的同时保证农户以及合作社的市场收益的增加,以保证农户和合作社的积极性。其次,重点发展区块链技术在市场需求对价格的敏感程度相对较低,以及农产品成本对质量提升的灵敏程度相对较低的农产品产业中的应用,利用区块链的技术优势创新发展区域性农产品品牌。再次,重点发展区块链技术在农产品市场对质量需求适中的农产品产业中的应用,以调动农户和合作社采纳区块链技术的积极性。最后,有效利用区块链技术优势,完善合作社内部运营体制机制,规范合作社运作程序。