具有输入时滞特性的列车自适应制动控制

2022-05-17谭畅李毅清

铁道科学与工程学报 2022年4期

谭畅，李毅清

(1.华东交通大学电气与自动化工程学院，江西南昌 330013；2.江西省先进控制与优化重点实验室，江西南昌 330013)

随着高速列车的运行速度逐渐提高，列车安全事故频繁发生，因此对列车的安全、平稳停车等问题提出了更高的要求，这一系列要求成为了保障列车正常运行的首要条件[1-2]。针对高速列车不同的运行环境，适时调整其制动力，实现列车安全、舒适等控制目标，是高速铁路的关键技术之一[3]。因此研究高速列车制动过程的建模与控制，对提高列车的制动性能和安全性具有重要的现实意义。目前，高速列车制动过程的建模和控制是主要研究方向。精确的制动模型是列车在制动控制器的作用下实现安全、平稳制动的重要保障。MAO等[4]考虑了高速列车的时变系统参数和未建模干扰，提出了对时变参数进行参数化的方法，设计了自适应故障补偿器。徐传芳等[5]提出了新的鲁棒自适应算法，分析了列车牵引与制动转矩产生的动态过程，考虑输入饱和约束及系统不确定性，设计鲁棒自适应动态面控制器以达到预期的速度位移跟踪控制。精确的模型与合适的控制方法是达到预期目标的必要条件。列车制动控制技术由传统的PID控制到模糊控制、自适应控制等智能控制算法[6]。吴萌岭等[7]提出了基于自适应参数估计的新型减速度控制模型，提高了制动控制系统对列车运行不确定参数的鲁棒性。张梦楠[8]考虑制动减速度难以准确测量以及制动装置的非线性特性，基于自适应PIQ技术和Back-stepping技术，设计了模型参考自适应停车控制器。罗恒钰等[9]构建基于增广误差的自适应控制系统，实现了制动系统的速度跟踪控制。TAN等[10]针对线性多变量对象，提出了基于模型参考自适应控制的多模型切换控制方案，设计控制切换机构以达到期望的控制性能。TAN等[11]针对离散多变量系统中由不确定性驱动时滞引起的结构不确定性问题，设计了自适应多模型控制器。国内外学者在高速列车的制动建模及控制器设计方面取得了不少成果，但鲜有考虑制动力产生时的动态过程，控制器设计方面也在很大程度上依赖参数已知的模型。自适应控制善于解决参数未知系统，因此，针对参数未知的系统采用模型参考自适应控制(MRAC)策略实现高速列车的制动控制是完全可行的。此外，高速列车制动时通过制动控制系统工作，而非直接操控动力执行机构，因此执行器的响应等过程会引起制动延时，从而影响列车安全运行。当前已有很多学者对时滞系统进行了研究。ZHOU等[12]针对具有未知时滞和输入饱和的非线性系统的自适应输出跟踪控制问题，采用模糊逻辑方法逼近系统的未知函数。XI等[13]研究了具有不匹配非结构非线性和未知时滞的高阶严格反馈系统的自适应渐近跟踪控制问题，利用自适应机制和投影算子估计未知时滞。郭红戈等[14]考虑制动信号指令的传输以及执行过程存在延时，基于动力学提出了高速动车组制动系统的Hammerstein模型。目前模型参考自适应控制常用于解决制动过程中的延时问题，但多数学者在建模时未考虑执行器延时，或者采用Pade逼近及泰勒展开忽略高次项等方法将制动延时近似处理，而忽略了短暂的延时也会给列车制动带来一定的影响，因此处理高速列车制动延时的速度跟踪问题十分有必要。本文充分利用自适应控制的优势，分析列车制动动态特性，考虑系统中含有未知参数和输入时滞，建立具有延时环节的制动模型，设计直接模型参考自适应控制器，实现高速列车对给定速度曲线的渐近跟踪，确保其安全制动。

1 问题的提出

本文研究的主要问题是含有输入时滞特性的高速列车制动系统的建模与控制问题。本节首先通过分析制动系统的原理和动态特性，建立精确的具有延时环节的线性制动数学模型；然后提出具有不确定参数和输入时滞的系统模型的控制问题和控制目标。

1.1 制动系统原理和动态特性

高速列车在制动时，首先采用电制动，制动指令并不能直接作用于列车的动力执行机构，而是由MBCU微制动控制单元接收列车司机或ATO发出的制动信号，通过收集此时的载重量m和车速v等，计算出所需制动力并调节其大小，从而控制列车的运行状态。

因此，可将列车制动系统表示为图1。

图1 列车制动系统示意图Fig.1 Schematic diagram of braking system of train

其中：m为载重量；u(t)为制动力指令；τ为动车组的延时时间，也称为空走时间；u(t-τ)为延时后的制动力指令；v(t)为列车此时实际速度；a(t)为此时的实际制动减速度。

1.2 列车制动系统模型的建立

根据图1可知，制动过程可分为以下4个环节。

1.2.1 接收制动信号环节

列车运行制动过程中首先由司机或ATO发出制动信号，MBCU微制动控制单元计算出当前制动所需要的制动力u(t)。

1.2.2 延时环节

制动系统计算出制动力指令u(t)后，会有一定的延时才能作用于执行机构，因此对于纯延时环节，系统的时域表达式为：

式中：τ为延时时间，u1(t)为延时后的制动力指令。

注释1.1：实际制动过程中，无论是电气制动装置还是空气制动装置，系统均存在延时环节[8]。

1.2.3 制动力生成环节

空走结束之后制动力逐渐增加，产生目标减速度a1(t)，根据文献[2]，高速列车的目标减速度与制动力的关系可近似为线性关系，用比例系数K表示，可描述为：

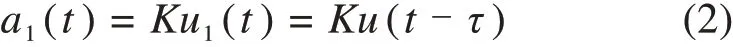
根据参考文献[14]，制动控制装置通过“反馈”作用实现实际制动减速度a(t)与目标制动减速度a1(t)的跟踪控制，动态过程由一阶惯性环节表示：

其中：T为制动系统时间常数。

注释1.2：在电制动系统下，所需制动力的计算值随着发电机电流以斜坡函数的形式产生。

1.2.4 积分环节

高速列车的实际制动减速度a(t)通过积分环节得到列车的实际速度v(t)。

由上述分析可得到制动系统模型框图如图2。

图2 高速列车制动系统模型框图Fig.2 Model diagram of braking system for high-speed train

根据模型框图并结合公式(1)～(4)可得到高速列车制动系统时域动力学模型为：

定义列车状态变量：x=[x1,x2]Τ=[v,a]Τ；则高速列车制动系统的状态空间描述为：

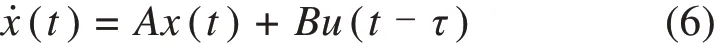
1.3 控制问题及控制目标

通过对列车制动系统的动态分析，考虑到高速列车运行环境复杂多变，制动系统存在大量不确定性，由于列车速度快，系统存在延时对于高速列车来说将会产生较大的影响。因此，鉴于模型参考自适应控制方法的独特优势，本文针对上述所建立的具有时滞特性的高速动车组制动模型(6)，设计合适的制动控制器，实现高速列车速度跟踪控制。

本文的控制目标为：通过模型参考自适应控制(MRAC)的方法，设计出基于状态反馈状态跟踪的自适应控制律u(t)，保证闭环系统所有信号有界，利用基于系统性能误差的自适应律进行参数更新，调整控制器参数，实现系统状态信号x(t)渐近跟踪一个参考模型状态信号xm(t)。

本文系统设计结构图如图3所示。

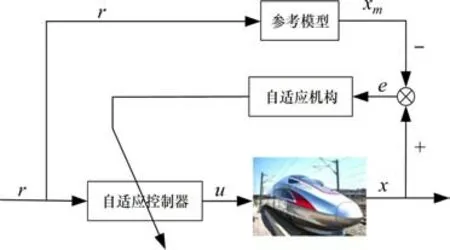
图3 高速列车模型参考自适应控制框图Fig.3 MRACdiagram of high-speed train

2 自适应制动控制器设计

上述通过分析列车制动系统具体的制动环节，建立了具有延时环节的制动模型，但系统中存在不确定的参数A和B。与传统的模型跟踪控制相比，MRAC有其特有的优势，当系统结构已知而参数未知的时候，它可以适应和调节外界环境对系统造成的影响，解决制动过程中的延时问题，确保系统达到或者接近理想状态。

基于控制目标，本文的控制器基本设计步骤如下：首先选取稳定的参考模型xm(t)；其次根据匹配方程进行系统参数化，基于系统参数化的模型，设计标称控制器；最后根据标称控制器形式得到自适应控制器，并设计自适应律更新控制器参数。

2.1 参考模型

为了设计模型参考自适应控制器，根据司机经验或前人研究给定期望的速度曲线，选择与系统结构相似并且稳定的参考模型：

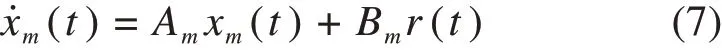
式中：xm(t)是参考输出信号，r(t)∈R是有界的外部输入信号，Bm∈Rn，Am∈Rn×n为稳定的矩阵。

注释2.1：传统的MRAC选择参考模型时，通常是任意设定一个外部输入信号r(t)，再根据式(7)计算得到参考输出xm(t)。而本文选择的参考模型，是通过给定xm(t)和参考模型系数(Am,Bm)，再由表达式(7)计算得到r(t)。

2.2 基本的匹配方程

鉴于状态反馈状态跟踪自适应控制方法结构简单且具有良好的瞬态性能，本节考虑延时已知的情况，采用上述方法设计控制器，且系统参数满足下列基本的匹配方程。

命题2.1：存在一个常值向量k*1∈R2和一个常值标量k*2∈R≠0，使得下列匹配方程成立：

当参考模型系数Am，Bm被选定且系统参数A和B已知时，常值矩阵k*1=[k*11,k*12]T和常数k*2可以通过式(8)计算得到。

2.3 系统参数化

为了设计自适应控制器，将列车制动系统进行参数化，未知的系统参数可表示为：

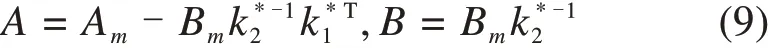
参数化之后系统模型可表示为：

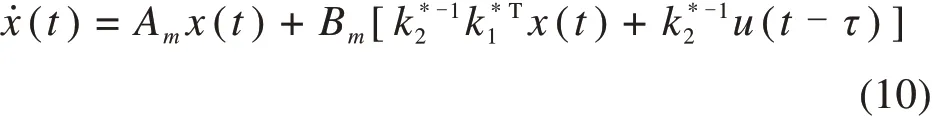
根据式(7)和(10)得到控制器结构为：

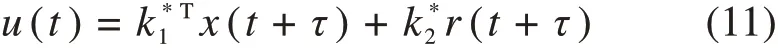
2.4 状态预测

由式(11)可知控制器中含有状态变量x(t+τ)，而延时会影响闭环系统的稳定性，因此需要对延时做处理，本文使用状态预测的方法，通过对控制输入在延时区间上的数值积分，预测系统状态变量。

假设已知制动系统初始状态x(t)，在控制器u(t)的作用下，预测τs之后的状态：

再利用黎曼和积分法进一步将(12)表示为：

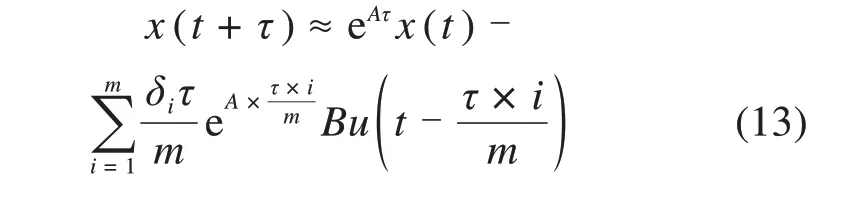
因此状态预测后控制器结构为：

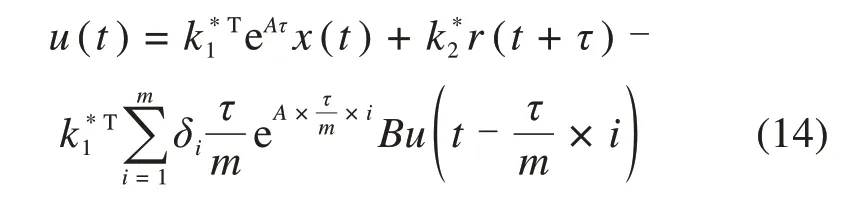
其中：δi为可调参数。

定理1[15]：考虑连续时间线性时不变系统ẋ=Ax+Bu，其状态运动规律为同时作用有初始状态和输入的状态方程的解，具体表达式为：

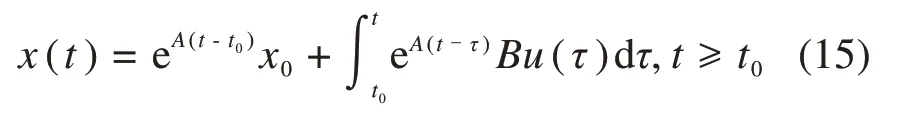
根据式(15)，通过变量替换可求解x(t+τ)。

注释2.2：黎曼和积分法的核心思想就是通过无限逼近来求解面积，也就是积分值。

2.5 标称控制器

根据系统参数化和状态预测之后的控制器结构(14)，为实现期望的控制目标，此时可设计标称控制器为：

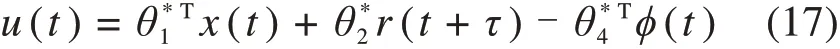
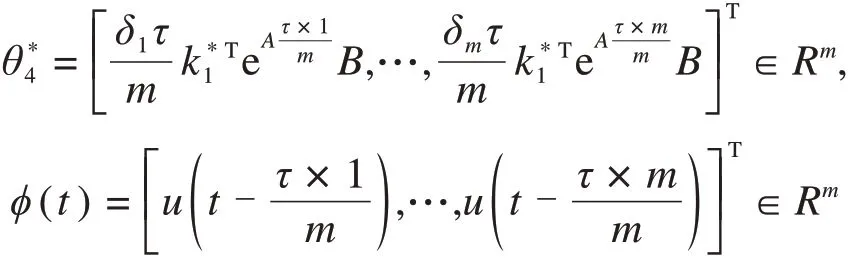
该标称控制器使得系统(6)所有的闭环信号有界，并且可实现期望的控制目标。

定理2[16]：标称控制器(17)作用于被控系统，则闭环系统(6)满足：

定义跟踪误差信号：

基于(7)和(19)，有：

由此可知，跟踪误差e(t)，状态向量x(t)和控制输入u(t)均有界，可得

2.6 自适应控制器

在实际制动过程中，制动系统的参数A和B未知，θ*1,θ*2,θ*4的值未知，因此标称控制器(17)不可实现。在此情况下，为了实现高速列车实际速度曲线渐近跟踪目标速度曲线，根据理想控制器的形式，可设计模型参考自适应控制器结构如下所示：

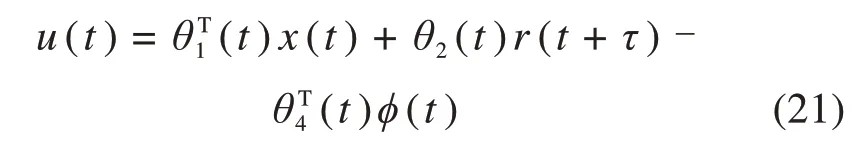
其中：θ1(t),θ2(t),θ4(t)为参数θ*1,θ*2,θ*4的估计值。通过更新自适应控制器参数，可以实现制动系统的速度跟踪控制。

2.7 自适应律

为了更新参数估计值θ1(t),θ2(t),θ4(t)，基于跟踪误差(19)，设计自适应律为：

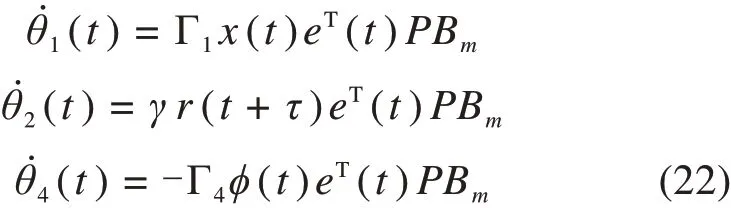
其中：Γ1∈Rn×n,Γ4∈Rn×n,γ∈R为自适应增益，满足：Γ1=ΓT1>0,Γ4=ΓT4>0,γ>0，P∈Rn×n，P=PT>0,Q=QT>0满足：PAm+ATm P=-Q。

为了分析式(22)中自适应律的性质，定义参数误差：

故跟踪误差方程：

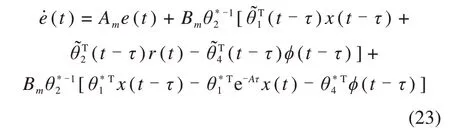
定义正定函数：

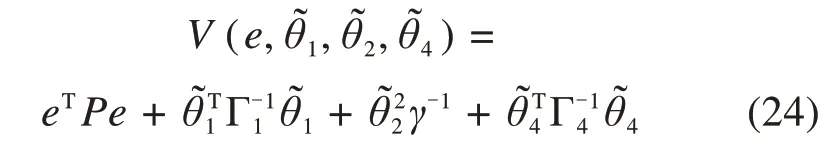
其中，Γ1∈Rn×n,Γ4∈Rn×n,γ∈R满足：

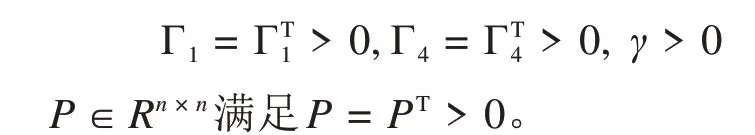
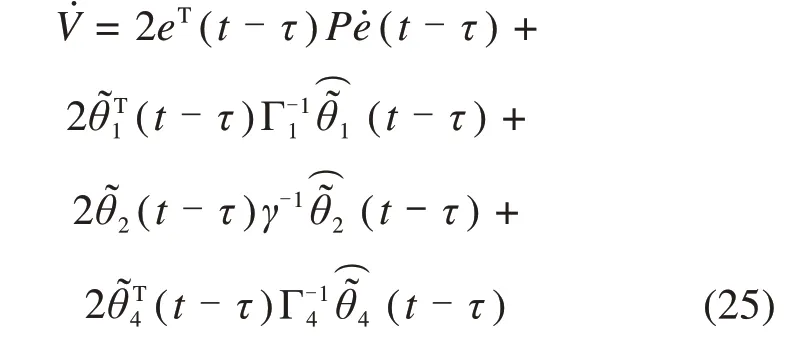
由于θ*1,θ*2,θ*4为常值，可得：

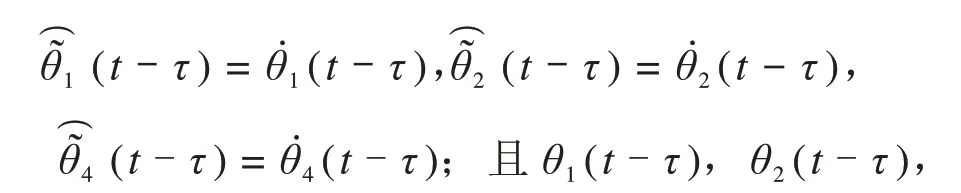
θ4(t-τ)满足式(22)。

故式(25)变为：

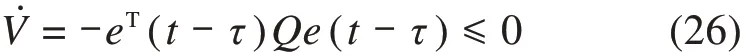
因此，θ1(t-τ),θ2(t-τ),θ4(t-τ)有界，即θ1(t)，θ2(t)，θ4(t)有界，θ1(t)∈L∞，θ2(t)∈L∞，θ4(t)∈L∞。

选择如式(22)的自适应律更新系统动态模型参数θ1(t),θ2(t),θ4(t)，可以得到不同时刻对应的控制器u(t)，作用于高速列车制动系统模型中，实现高速列车速度的实时跟踪控制。

2.8 稳定性分析

本文设计的高速列车自适应制动控制闭环系统具有如下期望的系统性能。

引理 1[16]：若̇(t)∈L∞，e(t)∈L2，则

定理3：针对具有不确定性参数和已知时滞的高速列车制动系统(6)，设计自适应制动控制方案，选择基于自适应律(22)进行参数更新的控制输入信号(21)，确保整个闭环系统信号有界，且

证明：信号有界可表述为该信号属于L∞信号空间，即：若，则z(t)∈R属于L∞信号空间。

由式(23)和(26)可知e(t)，e(t-τ)，ė(t)，ė(t-τ)，θ1(t),θ2(t),θ4(t)有界，有e(t)∈L∞⋂L2；根据式(19)可得状态信号x(t)也是有界的，因此式(21)中u(t)有界，闭环系统(6)稳定。再由引理1和式(19)可知即实现了列车实际速度对给定速度的跟踪性能。

综上所述，考虑存在系统延时的列车制动模型，采用直接MRAC设计控制器，将所设计的制动力u(t)作用于参数未知的列车制动模型，可以确保在所有闭环信号有界的前提下，其闭环系统是稳定的，继而实现高速列车实际速度渐近跟踪目标速度。并且本文未将制动延时近似处理，而是利用状态预测的方法求得延时之后的状态，使得所设计的控制器更加精确有效。

3 仿真分析

为了验证本文建立的含有输入时滞的系统模型的有效性，以及所设计的自适应控制器的期望性能，本节选用CRH380AL型高速列车制动系统为研究对象，采集列车制动时360组真实速度数据(济南―青岛)。基于上述理论分析，建立时滞制动模型，设计直接模型参考自适应控制器，利用MATLAB软件进行仿真验证和分析。

首先通过对采集的360组真实速度数据进行曲线拟合(单位为km/h)，可得到列车的理想制动速度曲线拟合结果如图4所示。

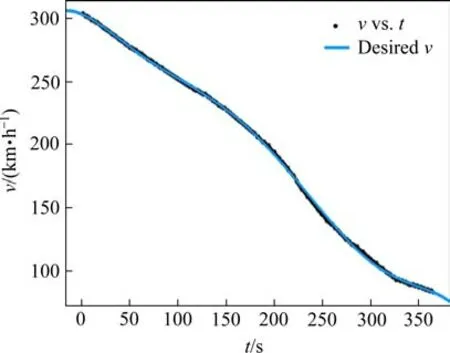
图4 速度拟合结果Fig.4 Velocity fitting result

系统模型动力学方程如式(6)所示，制动系统时间常数T=0.4 s，式(2)中比例系数K=0.9，制动系统输入时滞τ=0.2 s，因此公式(6)制动模型被描述为：

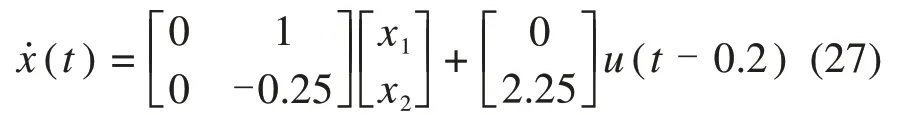
其次，根据设计要求选择参考模型(7)中的参数Am,Bm，取：参考模型(7)被描述为：

外部输入信号r(t)通过式(28)计算得到；

接下来选择状态预测时公式(13)中参数取值：m=10，δi=(i-0.5)(i=1,…,m)。

最后选取合适的状态初值：x(0)=[304,0]，xm(0)=[303.8,-0.326 4]；参数估计初值与其真值之间的关系为：θ1(0)=90%θ*1，θ2(0)=89%θ*2，θ4(0)=90%θ*4；自适应增益设计为：Γ1=5I，γ=0.075，Γ4=0.7×10-4I。利用所设计的自适应控制器对制动模型进行速度跟踪控制，得到如下仿真结果，分别为列车速度和加速度的跟踪响应和跟踪误差，并且进一步仿真了制动位移的跟踪情况。

通过对仿真图进行分析，速度、加速度和位移跟踪误差均在列车开始制动时最大，图5中最大速度跟踪误差约为0.31 km/h，图6中最大加速度跟踪误差约为0.09 m/s2，图7中最大位移跟踪误差约为1.9 m，各仿真状态量的误差均在允许的最大范围之内，满足系统的跟踪控制要求；随后在短时间内进行参数调节，约12 s左右误差趋近于0并达到稳定状态，实现了列车速度、加速度以及位移跟踪控制的目标，系统的控制性能十分理想。并且由图6可以看出，列车制动时加速度曲线平缓，变化缓慢，保障了列车的安全制动，也提高了列车制动时的平稳性。因此本文设计的自适应制动控制策略在系统存在不确定性参数以及输入时滞的情况下，仍然能保证所有的闭环信号有界，并且能够对给定的速度曲线进行渐近跟踪，达到系统的控制目标，实现安全平稳的制动要求。

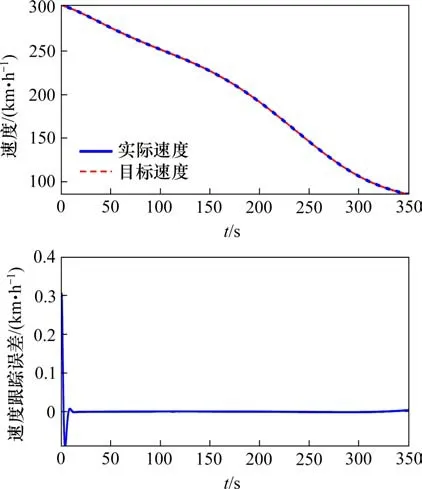
图5 列车速度跟踪及误差Fig.5 Train speed tracking and error

图6 列车加速度跟踪及误差Fig.6 Train acceleration tracking and error

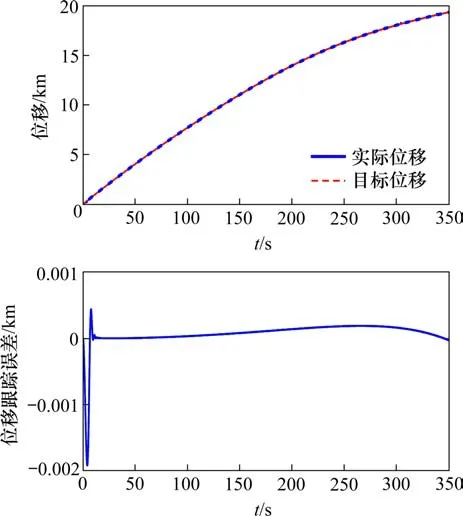
图7 列车位移跟踪及误差Fig.7 Train displacement tracking and error

为了验证本文所设计的模型参考自适应控制策略处理参数不确定系统以及时滞问题的独特优势，以下采用Back-Stepping滑模控制算法、基于自适应PIQ技术和Back-Stepping技术的控制方法、以及基于增广误差的自适应控制方法与本文的控制算法进行对比，实验仿真了具有代表性的各个状态向量的跟踪误差，图8是采用Back-Stepping滑模控制算法的仿真结果，图9是采用基于PIQ技术和Back-Stepping技术的控制方法的仿真结果，图10采用基于增广误差的自适应控制方法的仿真结果。

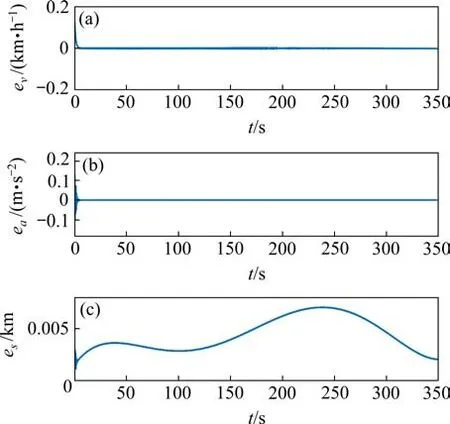
图8 采用Back-Stepping滑模控制算法Fig.8 Using Back-Stepping sliding mode control algorithm

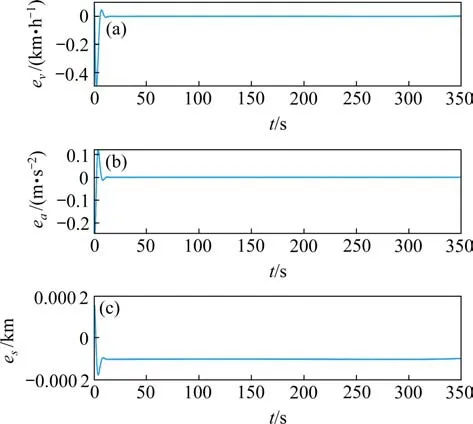
图9 采用基于PIQ技术和Back-Stepping技术的控制方法Fig.9 Control method based on PIQand back-stepping

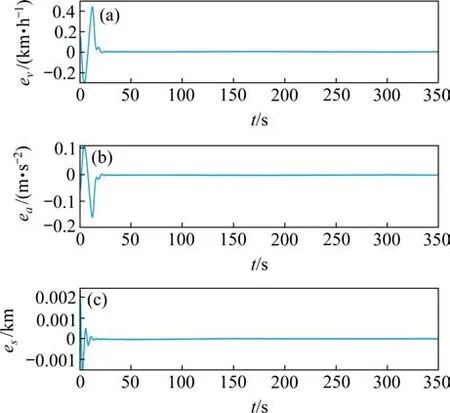
图10 采用基于增广误差的自适应控制方法Fig.10 Adaptive control method based on augmented error

图8表明，采用Back-Stepping滑模控制算法进行动车组制动控制时，其速度的最大误差虽然较小，但收敛之后存在抖动；加速度最大误差达到了0.25 m/s2，在制动开始时抖动较大；位移最大误差约为7 m，但其随着制动减速度的变化而变化，制动系统稳定性不够好。图9表明采用基于PIQ技术和Back-Stepping技术的控制器时，系统也能够实现速度的渐近跟踪控制，但速度和加速度的最大误差相对本文的控制算法来说较大，且系统存在稳态误差，位移误差渐近收敛于原点附近的邻域0.1 m。图10表明采用基于增广误差的自适应控制器在制动调节时比较平稳，同样能够实现速度的渐近跟踪，但各状态向量的误差收敛时间较本文算法更长，约20 s左右误差趋近于0并达到稳定状态；最大速度跟踪误差约为0.44 km/h，在收敛初期有短时间的轻微抖动；并且其瞬态响应不够理想，初始控制误差较大，初始位移误差达到了2.4 m。而本文设计的控制算法速度跟踪时最大误差小，精度高，加速度变化缓慢，列车制动时平稳运行，12 s左右速度误差和加速度误差以及位移误差便趋向于0，达到稳定状态。因此，本文采用的模型参考自适应制动控制算法不仅可以处理系统参数不确定性和输入时滞问题，实现对列车制动速度的渐近跟踪，而且跟踪精度也更高，列车运行时更加平稳，制动性能更优越，列车的瞬态性能得到了改善。