一类非局部微分方程在Orlicz空间中吸引子的存在性

张昶

（江苏理工学院 数理学院，江苏 常州 213001）

设Ω是ℝn中的有界光滑区域。本文主要考虑非局部反应扩散方程在Orlicz空间中全局吸引子的存在性：

这里u0∈L2(Ω)，0<σ<2。假设g满足自然的耗散条件：

这里q>1，C0和k0是正常数。

经典的反应扩散方程（σ=2）常应用于物理学、化学及生物学等领域，一直是无穷维动力系统的重要研究对象，并产生了许多研究成果[1-6]。这些成果对吸引子问题的研究主要集中在L2(Ω)、Lp(Ω)和空间中。近年来，由于非局部耗散的微分方程，特别是带有分数次Laplace算子的微分方程，能够更有效地解释物理学、金融学、生态学及地球物理学等学科领域的问题，因而受到广泛关注[5，7-11]。但是，这些成果对吸引子的研究也大多集中在Lp(Ω)空间、Sobolev空间及分数次Sobolev空间中，对于Orlicz空间中吸引子的研究相对较少。

本文主要研究在条件（2）下非局部微分方程（1）的长时间动力学行为。首先，由非线性项确定一个Orlicz空间；其次，在该Orlicz空间中证明弱解的存在性；再次，通过L2-L∞估计，得到当t>0时，弱解也在L∞(Ω)空间中；然后，通过证明解在L∞范数下的一致有界性，得到了L∞(Ω)-有界吸收集的存在性，进一步得到在任意给定的Orlicz空间中有界吸收集的存在性；最后，在Orlicz空间中建立了半群{S(t)}t≥0的渐近紧性，进而得到了全局吸引子在Orlicz空间中的存在性。

1 预备知识

1.1 分数次Laplace算子

1.2 Orlicz空间

设p(t)为单调增加，t≥0时右连续，t>0时函数值大于0，且p(0)=0，，则称函数为N-函数。容易验证N-函数是凸函数。记，那么q(s)与p(t)具有相同的性质。因此，可以得到另外。M(u)和N(v)称为一个N-函数互补的N-函数。

引理1[12]：如果存在正数u0和k，使得当u≥u0时p1(u)≤p2(ku)，那么M1(u)≺M2(u)。

设D为n维欧几里得空间（赋予Lebesgue测度）中的有界集。将所有满足ρ(u；M)=∫DM[u(x)]dx<∞的实函数全体记为LM(D)，称LM(D)为Orlicz类。Orlicz类LM(D)一定是凸集，但不一定是向量空间。为了得到向量空间，设M(u)和N(u)是互补的N-函数，将满足

的函数u(x)全体记为。显然，是线性空间。在这个线性空间上赋予范数

以下几个引理将在后文中起到重要作用。应用Young不等式，可以得到下面引理。

引理2[12]：对于任意函数u(x)∈LM，有

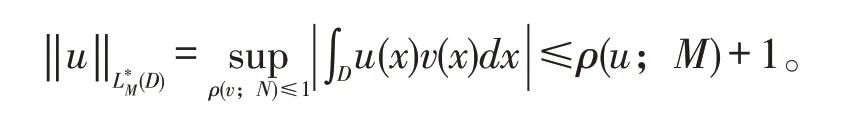
由引理2知Orlicz类LM(D)包含于Orlicz空间。

引理3[12]：如果M1(u)≺M2(u)，那么；进一步，存在常数C>0使得。

引理4[12]：设M(u)和N(u)是互补的N-函数，κ(E)是E(⊂D)上的特征函数，那么

这里m(E)是E的测度。

2 适定性

首先给出问题（1）弱解的定义。

定义5：如果函数u(x，t)满 足：（a）；（b）在分布意义下u(x，t)满足方程（1），并且u(x，0)=u0∈L2(Ω)。那么，u(x，t)称为问题（1）的弱解。

下面的定理给出了非局部微分方程解的存在唯一性。

定理6：如果Ω是ℝn中的有界光滑区域，g满足条件（2），那么，对于任意的初值u0∈L2(Ω)和任意的T>0，存在唯一的弱解u使得：

并且映射u0→u(t)在L2(Ω)上是连续的。

证明：应用标准的Galerkin方法[5，13]可以得到解在L2(Ω)和中的存在性。

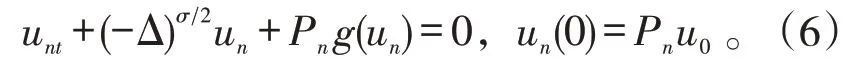
在方程（6）两端乘以un，并且关于Ω积分，可得：

结合条件（2），可知：

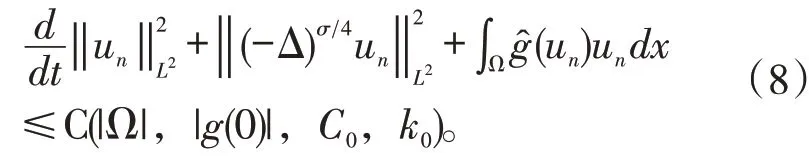
应用引理2、不等式（9）和（10），就有：

将上式两端在0到T上关于t积分，再应用引理1和引理3，可得：

再证明解u(t)关于时间在L2(Ω)上的连续性。将方程（6）两端乘以unt，并且关于Ω积分，可得：

再将上式关于变量s在(0,T)上积分，可知：

另外，应用不等式（8）得到：

注意到：

再结合（12）和（15），就有：

因此，对于任意的ε∈(0，T)，有：

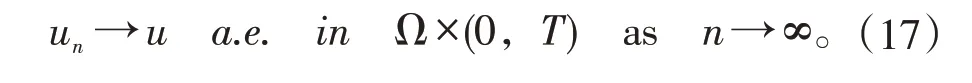
进一步，应用对角化方法得：

为了说明g(u)∈L1(0，T；L1(Ω))。令χΩ1和χΩ2是集合Ω1={(x，t)∈Ω×(0，T)：|un|>1}和Ω2={(x，t)∈Ω×(0，T)：|un|≤1}的特征函数。因为，这里C不依赖于n，所以有：

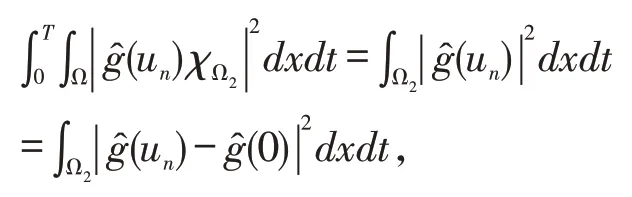
应用中值定理，得到：

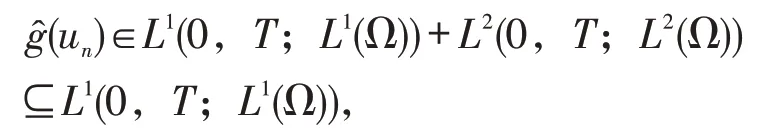
再由Fatou引理：

又因为：

u∈L∞(0，T；L2(Ω))⊂L1(0，T；L1(Ω)+H-σ/2(Ω))，所 以u∈C([0，T]；L1(Ω)+H-σ/2(Ω))，这便得到u∈Cs([0，T]；L1(Ω)+H-σ/2(Ω))。运用文献[14]中的引理8.1知：

进而有：

将方程（6）两端乘以检验函数ϕ(x)η(t)并积分。这里，，η∈C1[0,T]，并且η(T)=0，可得：

同样地，对于任意的ε>0，有：

在上面两式中令n→∞，可得：

和

再在（20）中令ε→0+并且应用（18），可得：

结合（19）和（21），可知u(0)=u0。再将（8）在[0,T]上关t积分，有：

令n→∞，得：

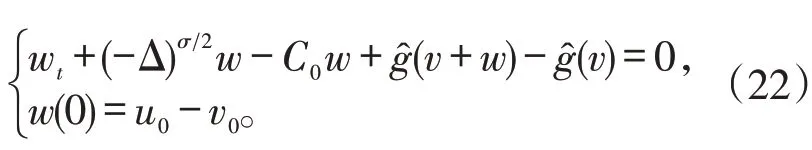
定义一个截断函数：

应用文献[16]中Remark 2.1，可知：。在方程（22）两端乘以ψk(w)，并且在Ω×(0，T)上积分，可得：

由ψk(⋅)的定义知：

因此，

再令上面的不等式中k→∞且ε→0，那么

又由Gronwall不等式知：

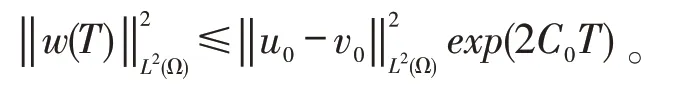
这便得到了解的唯一性和连续依赖性。

应用定理6，可以在L2(Ω)中定义一个连续半群{S(t)}t≥0，即

3 全局吸引子

本节主要研究在Orlicz空间中吸引子的存在性。先来证明(L2(Ω)，L∞(Ω))-有界吸收集的存在性。

引理7：设条件（2）成立，u0∈L2(Ω)。如果u(t)是方程（1）的弱解，那么存在常数M使得：

这里，M依赖于t-1但不依赖于。

再把上面的不等式两端乘以sk，并且关于变量s在[0,t]上积分，可知：

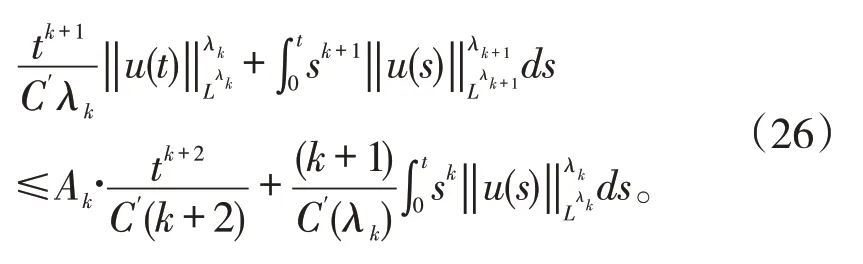
另外，由不等式（9）得：

迭代不等式（26）并结合不等式（27），则有：

这里，

再将不等式（28）两端除以tk+1并且开λk次方根，得到：

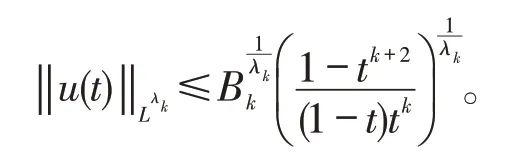
令k→∞，当t>0时，有不等式

引理7说明当t>0时u(t)∈L∞(Ω)，并且得到了解的只依赖1t的L∞上界。这便意味着(L2(Ω)，L∞(Ω))-有界吸收集是存在的。因为任意给定的Orlicz空间都包含L∞(Ω)，所以-有界吸收集也是存在的。

应用(L2(Ω)，L2(Ω))-全局吸引子的存在性来证明半群在Orlicz空间中的渐近紧性，(L2(Ω)，L2(Ω))-全局吸引子的存在性可由文献[5]中的方法得到。

定理8：半群{S(t)}t≥0存在(L2(Ω)，L2(Ω))-全局吸引子。

引理9：设{un}是L2(Ω)中的Cauchy列，{un}在L∞(Ω)空间中一致有界，即存在常数K使得‖un‖L∞≤K，∀n∈ℕ。那么，{un}也是Orlicz空间中的Cauchy列。

证明：设N(u)是与M(u)互补的N-函数，那么，。因此，定义任意的ε>0，总存在δ1>0使得

由于N-1是凹函数，所以N-1(αu)≥αN-1(u)，(0<α<1)。这是因为当变量u>0时，函数N-1(u)/u是单调减函数，即：

因为{un}是L2(Ω)中的Cauchy列，所以un是依测度收敛的。因此，令

存在N>0，使得任意的n，m>N，那么有：

记Eδ={x∈Ω：|un-um|≥δ}，那么有：

因此，{un}是中的Cauchy列。

应用文献[3]中的方法容易得到下面的引理。

引理10：设{S(t)}t≥0是L2(Ω)中的连续半群，也是中的半群。如果{S(t)}t≥0存在(L2(Ω)，L2(Ω))-全局吸引子，并且满足：（a）{S(t)}t≥0存在(L2(Ω)，-有界吸收集B0；（b）{S(t)}t≥0是(L2(Ω)，-渐近紧的。那么，{S(t)}≥0存在(L2(Ω)，-全局吸引子。

结合引理8—10，就可以得到本文主要结论，即定理11。

定理11：设g满足条件（2），则对于任意给定的Orlicz空间，方程（1）生成的半群{S(t)}t≥0存在(L2(Ω)，-全局吸引子。