基于AF和AS算法优化的slam_gmapping研究

颜 韩，汪 伟，崔金华，代迪迪，王汝佳

（江苏理工学院 汽车与交通工程学院，江苏 常州 213001）

近年来，随着人工智能技术的快速发展，移动机器人被广泛应用于工业生产中，如仓储搬运机器人、扫地机器人等，为人们提供了切实的便利。但是，随着“智能制造2025”的提出，传统的磁导、惯导技术已经无法满足人们的需求，人们渴望机器人能够无时无刻在任何环境中进行自主定位与导航。

即时定位与建图（SLAM）技术为自主定位与导航提供了扎实的理论基础。SLAM具体指机器人凭借自身的传感器（激光雷达或者摄像头等）感知环境信息，并进行自主定位与建图。SLAM技术最早由Smith等人[1]提出，之后一直受到相关行业研究者的关注。早期的滤波研究着重于卡尔曼滤波，但是人们逐渐意识到卡尔曼滤波在处理非线性、非高斯噪声时的局限性[2]。因此，粒子滤波（Particle Filter，简称PF）应运而生。粒子滤波也叫顺序蒙特卡洛方法，该方法是通过一组在状态空间中传播的随机样本近似地表示概率密度函数，从而实现系统的状态估计[3]。由于粒子滤波在处理非线性系统方面具有得天独厚的优势，所以被广泛应用。Murphy等人[4]第一次提出RBPF算法，该算法创造性地将定位与建图分开，即先利用自身传感器进行定位，再依据定位进行环境建图，最后融合建图对定位进行修正。Grisetti等人[5]提出了Gmapping算法，该算法在RBPF算法基础上提出改进提议分布和选择性重采样；实验结果表明，这种方法不仅有效减小了系统的计算量，而且有利于缓解粒子退化和粒子多样性减少的问题。相较于国外，国内对于SLAM的研究虽然起步较晚，但是发展迅速，如何佳泽、张寿明[6]针对传统RBPF-SLAM算法构建地图存在重影、粒子出现衰退等问题，设计了阈值重采样函数进行优化采样。章弘凯等人[7]针对2D激光SLAM机器人导航中激光点云匹配计算量大、轨迹闭合效果差、位姿累积误差大等问题，提出一种基于多层次传感器数据融合的实时定位与建图方法——Multilevel-SLAM；实验结果表明，Multilevel-SLAM算法有效提高了闭环处的轨迹闭合效果，具有更低的定位误差。丁元浩等人[8]针对室内环境下的2D激光同步定位与构图问题，提出一种改进的扫描匹配方法，扫描到子图匹配；实验结果表明，该方法可以有效提高定位与制图的精度和激光匹配效率。

虽然越来越多的学者对SLAM展开了深入的研究，但是Gmapping算法在高相似度、多闭环等复杂环境下，仍存在建图效果不太理想甚至建图失败的问题。针对此问题，郑兵等人[9]提出将萤火虫算法（AF）与Gmapping相融合的算法。但是，该方法与RBPF、Gmapping算法一样都存在粒子数恒定的问题。所以，本文尝试提出了一种自适应采样（Adaptive Sampling，简称AS）算法，即当二维激光点云波动量大于某个阀值时，增加采样粒子数，反之适当减少采样数。此外，为了使系统在复杂环境中有更好的建图效果，本文还将AS、AF与Gmapping相融合，进而提高系统复杂环境的建图能力。

1 传统Gmapping算法

1.1 RBPF算法

众所周知，SLAM问题的核心是如何利用观测量和运动控制量来求解系统的位姿和地图的联合分布P（X1:t,m|Z1:t,U1:t−1），而同时求解X1:t和m很难。因此，Murphy等人[4]提出了RBPF算法，该算法运用概率论的思想来分解问题，即将联合后验概率分解成两个后验概率密度乘积的形式，如公式（1）所示：

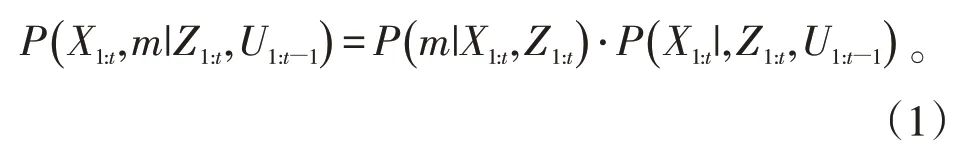
其中：P(X1:t|,Z1:t,U1:t−1)代表定位的问题，即机器人系统利用自身传感器（里程计、激光或者摄像头）信息对位姿进行估计定位；P(m|X1:t,Z1:t)，即机器人依据位姿信息进行增量式地图m的创建。

1.2 改进提议分布

由上述RBPF算法可知，为了估计下一时刻的位姿，需要从提议分布中采样，因此提议分布的精确程度对系统位姿估计具有举足轻重的作用。而RBPF中的提议分布仅仅考虑了里程计信息，随着时间的积累会产生很大的误差，导致其采样粒子无法准确估计系统当前的状态。Gmapping算法在RBPF的基础上将最近一次的观测信息融入到提议分布中，但由于激光观测的数据是360°无死角的距离信息，在实际情况下无法进行运动模型的建立，而且当观测概率比较尖锐时，会产生和RBPF算法一样的缺陷——计算量太大。所以，提出可以直接从峰值附近采K个值来模拟出提议分布，优化后的高斯函数提议分布如下：

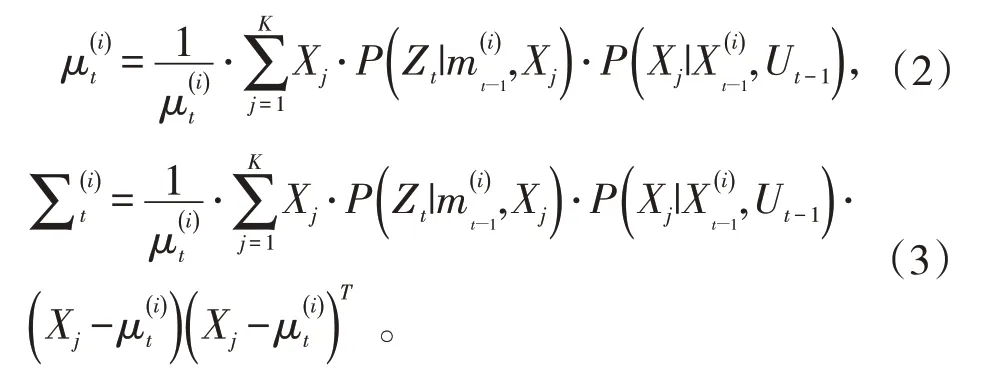
进一步优化后的权重递推公式就变成了：

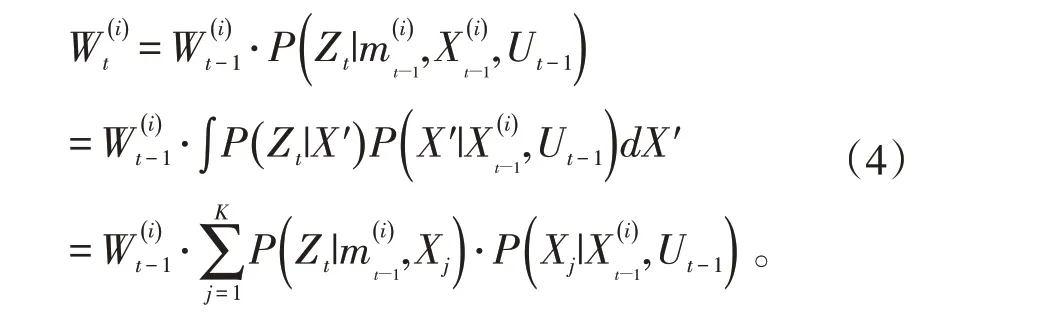
1.3 选择性重采样

RBPF算法根据每个粒子的权重进行重采样，保留权重值大的粒子，并复制权重值大的粒子代替权重小的粒子，使粒子的分布更加接近真实情况。但是，频繁的重采样会使系统的运算量激增。同时，也有可能会滤去权重小的但更接近真实情况的粒子，使粒子退化和粒子多样性减少。Gmapping算法在此基础上融合了理论判定方法，提出了有效粒子数Neff的概念，设定只有当有效粒子数低于某个阀值B时，才会进行重采样操作。有效粒子数计算公式如下：

2 Gmapping算法的优化

2.1 自适应采样

由前文可知，传统Gmapping算法在RBPF的基础上改进了提议分布和选择性重采样，极大缓解了粒子退化和粒子多样性减少的问题。但是，由于算法中的采样粒子数仍是固定不变的，而现实环境是复杂多变的，因此，以固定的粒子数构建复杂多变的环境地图，不但会造成计算资源的浪费，而且也难以保证复杂环境的建图完整性。

针对上述问题，本文提出了一种自适应采样（Adaptive Sampling，简称AS）算法，将采样粒子数和现实环境的复杂程序进行线性拟合，当二维激光点云波动量大于某个阀值时，增加采样粒子数，反之适当减少采样数。算法运行步骤为：当系统启动时，里程计和激光雷达采集周围环境信息，首先将激光点云进行线性拟合处理，进而判断点云线性的波动量；当波动量小于阀值X’时，认定外界环境为简单环境，此时减小采样粒子数，达到减少系统运算量的目的；当点云波动量超过阀值时，增加采样粒子数，进而增强系统对于复杂环境的定位与建图效果；接着再进行点云匹配、权重计算、重采样（由有效粒子数Neff决定）、地图更新等操作。具体流程如图1所示。

自适应采样算法能够充分合理地利用系统资源。在简单环境中，线性地减少采样粒子数，进而缓解系统资源的压力，同时减少定位和建图时间；在面临多闭环、高相似复杂环境时，也能有较好的建图效果。除此之外，经过预处理的激光点云高度线性化，能够极大地减少扫描匹配阶段的匹配时间。因此，该方法能够有效缓解采样粒子数恒定导致的运算资源浪费问题，同时也能够增强系统面对复杂环境的建图能力。

2.2 萤火虫算法及优化

萤火虫算法（Firefly Algorithm，简称FA）最早是由崔昊杨[10]根据萤火虫的发光特性提出的，其主要原理是利用发光强的萤火虫吸引发光弱的萤火虫，使发光弱的萤火虫移动到最佳位置，以此来达到寻优的目的。

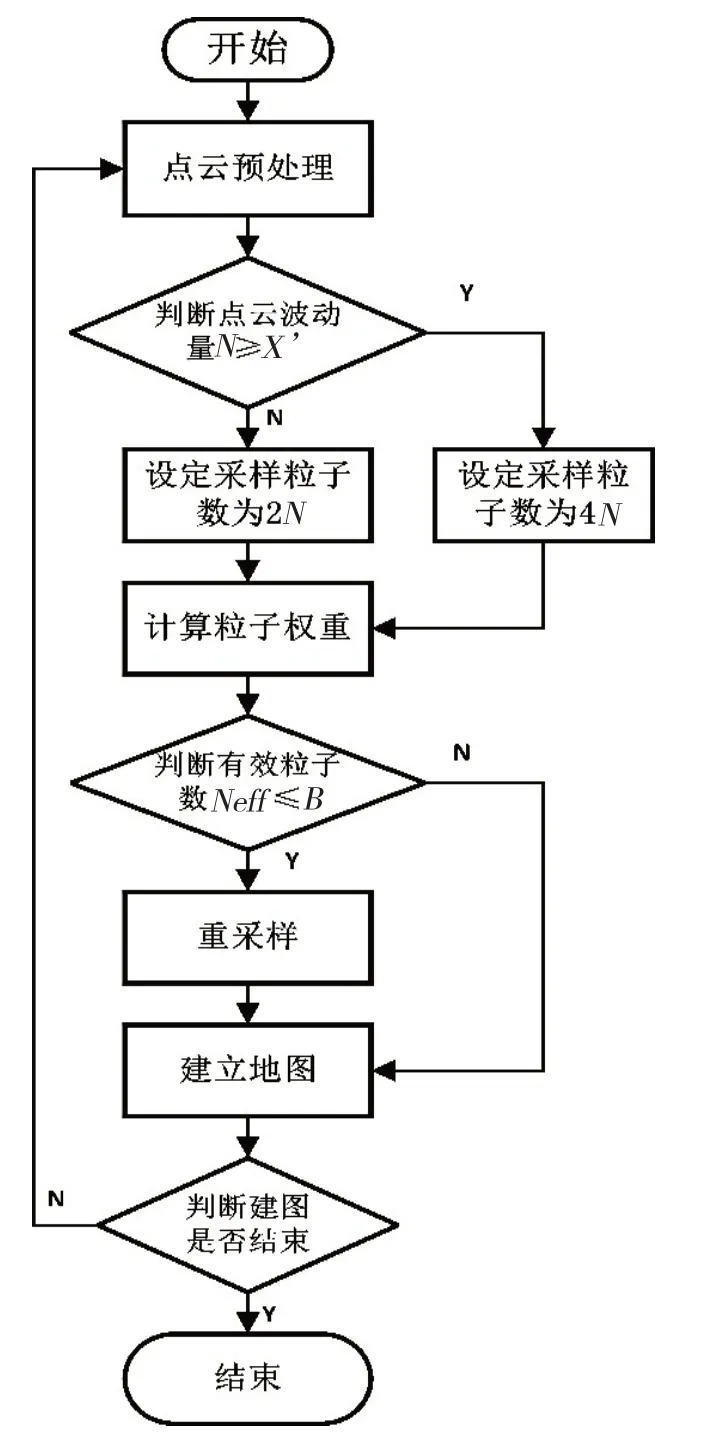
图1 自适应采样算法流程图

萤火虫算法的数学描述中涉及的两个重要参数是发光强度和相互吸引度，其计算公式如下[11]：

其中：I表示萤火虫的相对发光强度；I0表示最亮萤火虫的亮度，即r=0处的荧光强度；γ表示光吸收系数，此参数是为了体现荧光会随距离的增加而逐渐减弱的特性；rij表示萤火虫i和萤火虫j之间的距离；β()r表示萤火虫之间的相互吸引度；β0则表示最大吸引度，即r=0处的吸引度。

此外，该算法是通过迭代的方法不断使发光弱的萤火虫移动到最优位置，其最优目标迭代公式如下[12]：

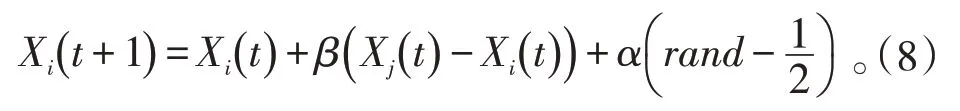
其中：Xj(t)，Xi(t)分别表示t时刻萤火虫j和i的空间位置；α为步长因子；rand则为[0，1]上服从均匀分布的随机因子。一般萤火虫算法的伪代码如表1所示[13]。

表1 萤火虫算法的伪代码

本研究中，为了增强复杂环境的建图效果，引入萤火虫算法对粒子进行寻优操作，具体包括两部分：区域划分和选择性寻优。首先，本文将粒子权重与萤火虫荧光亮度参数进行信息交互，并根据亮度值将粒子划分为高相似区和低相似区，同时，分别计算出高相似区和低相似区的局部最优值，并进行局部寻优操作。由于在寻优过程中要不断计算出两两粒子的相对亮度与吸引度，从而使得系统的计算量大大增加。

文献[14]提出将全局最优值与各粒子进行信息交互的方法，使每个粒子只和全局最优粒子进行信息交互，其位置迭代公式如下：

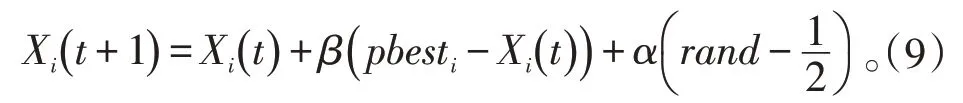
其中，pbesti表示全局最优粒子的状态值。此方法避免了两两粒子之间反复的计算过程，将各粒子只与全局最优粒子进行信息交互，大大减小了系统的计算量，是切实可行的。

此外，为了防止萤火虫算法因高寻优性能导致粒子多样性减少的问题，本文设置了一个阀值Nf，当局部粒子数超过阀值Nf时，则停止寻优操作；反之，则继续进行寻优操作，直至达到迭代次数或者寻优精度。此方法在防止粒子多样性减少的同时，也能够减少粒子的寻优速度，进而减少系统的计算量。

基于萤火虫算法（FA）和自适应采样（AS）算法优化的slam_gmapping算法具体步骤如表2所示。

3 仿真实验与结果分析

3.1 实验平台与仿真环境

本文中仿真实验是以Ubuntu20.04操作系统为基础，运用Noetic版本的ROS平台及系统自带的Turlebot机器人模型展开实验，同时综合运用RVIZ、Gazebo和rqt等可视化模块进行实验探索和分析。在Gzaebo中，通过Building Editor模块搭建简单和复杂的物理仿真环境；在RVIZ和rqt中观察算法的建图效果。机器人仿真模型如图2所示，简单、复杂的物理仿真环境如图3、图4所示。

表2 优化后的slam_gmapping算法的具体步骤

图2 Turlebot机器人模型图

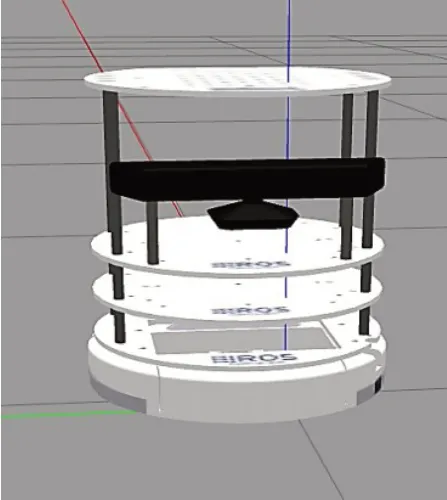
图3 简单的物理仿真环境

图4 复杂的物理仿真环境

3.2 实验结果与分析

仿真实验主要包括三个方面；研究优化算法的定位精度；比较传统Gmapping算法、文献[9]中单纯融合萤火虫算法的Gmapping算法与本文优化后的算法在简单环境中的建图时间与效果；对比3种算法在多闭环、高相似度环境中的建图效果与平均建图时间。

3.2.1 优化算法定位精度研究

为了验证优化算法定位系统的可靠性与定位精度，选取在复杂环境中从起点沿预计轨迹运动到终点的方案。采用A*算法进行轨迹路线的预估，运用move_base控制方法探索优化算法位置的定位精度。如图5所示：图中绿色轨迹表示A*算法预估的轨迹路线，图中①和②代表机器人的起点和终点。图6为系统X，Y方向定位误差曲线 图，表3为系统预估值与真实定位值对比表。

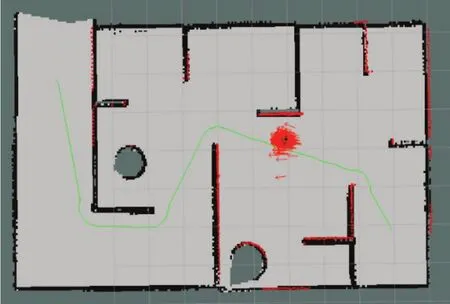
图5 机器人轨迹路线图

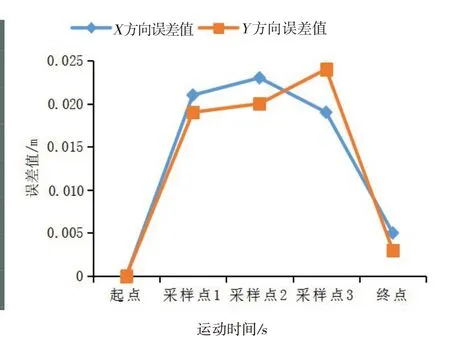
图6 X，Y方向定位误差曲线图

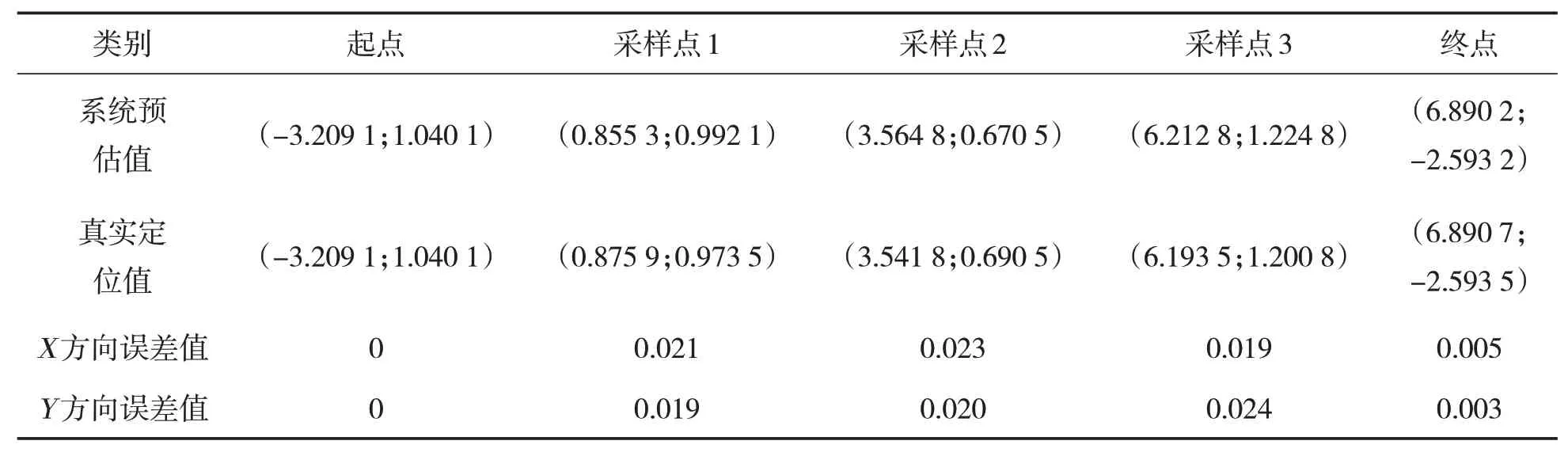
表3 系统预估值与真实定位值对比表

由图6可知，随着运行时间的增加，系统定位误差值也逐渐增加，在采样点3处达到最大值0.024 m；但是，从采样点3开始误差值逐渐减少，这是因为终点约束对机器人的影响逐渐增大，迫使机器人运动到终点位置。此外，由表3可以看出，系统的X，Y方向的平均定位误差分别为0.013 6 m和0.013 2 m，表明系统定位真实值与系统预估值吻合度较高，可满足一般环境的定位要求。

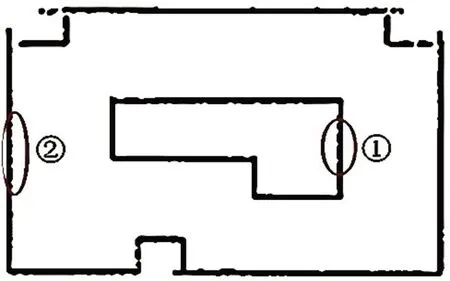
图7 传统算法在简单环境的建图效果

3.2.2 对比3种算法在简单环境中的建图效果

为了确保传统Gmapping算法和单纯融合AF的Gmapping算法的建图效果，选取50个粒子作为实验参数，而改进后的算法无需给定粒子数。此外，经多次实验发现，点云波动量阀值X’为12时建图效果更佳。3种算法在简单物理环境中的建图效果见图7、图8、图9，其平均建图时间对比如表4所示。

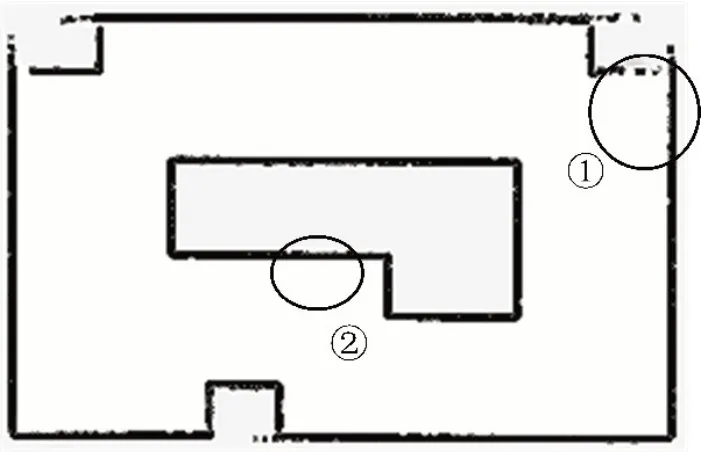
图8 文献[9]算法在简单环境的建图效果

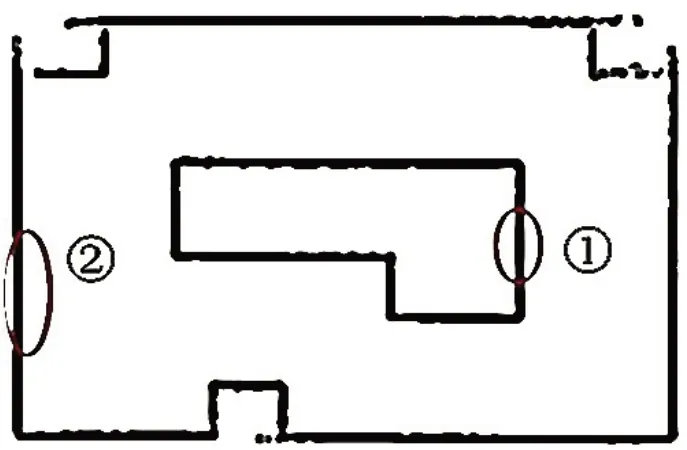
图9 优化后算法在简单环境的建图效果

表4 3种算法在简单环境建图时间对比表

从图7、图8、图9可以看出，改进后的算法在简单物理环境中的建图效果比传统算法和单纯融合AF的Gmapping算法有所增强，其建图能力能够满足现实需要。从表4可知，优化后的算法其采样粒子数明显减少，平均建图时间为362 s，相比传统算法和单纯融合AF的Gmapping算法分别缩短了约14%和7%。但是，优化后的算法增加了代码的数量和执行步骤，即增加了系统的复杂度，这也是其建图时间缩短的幅度没有文献[2]那么大的原因之一。

3.2.3 对比3种算法在复杂环境中的建图效果

针对传统Gmapping算法在复杂环境建图效果不佳的情况，本文将萤火虫算法与Gmapping算法融合，利用萤火虫算法的集聚能力，增强算法的建图能力。但是，萤火虫算法是通过不断迭代的方法寻优的，所以合理地选择迭代次数，有利于缩短算法的建图速度。通过多次实验发现，在上述复杂环境中，4次迭代数在节省建图时间的同时也能够满足建图的需求，故本实验选择迭代次数为4次。此外，因为萤火虫算法集聚能力过强，为了避免粒子多样性缺少，本文将迭代终止阀值设置为0.02。3种算法在复杂环境的建图效果见图10、图11、图12，其建图运行时间对比见表5。

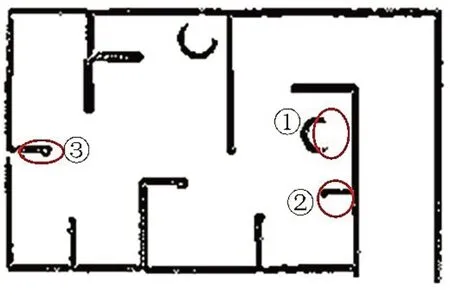
图10 传统算法在复杂环境的建图效果

从图10、图11、图12可以看出，优化后算法的建图效果比传统算法更优，将墙壁的厚度都能详细描述出来，且建图也更加完整。此外，从表5可以看出，优化后的算法在面临复杂环境时，平均建图时间为408 s，相比传统算法和单纯融合AF的Gmapping算法，其建图效率分别提高了约3%和0.9%。需要说明的是：由于本算法在面临复杂环境时融合了自适应采样和萤火虫算法，导致采样粒子数和代码复杂度略微增加；但是，经过预处理的激光点云高度线性化，能够极大减少扫描匹配阶段的匹配时间，因此其平均建图时间则有所缩短。

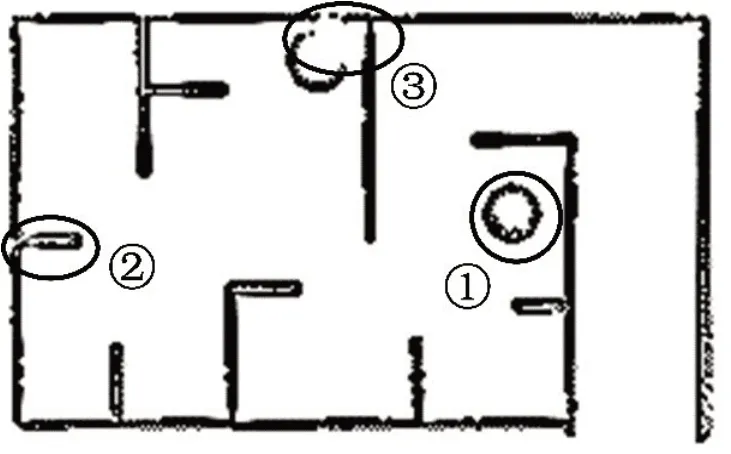
图11 文献[9]算法在复杂环境的建图效果

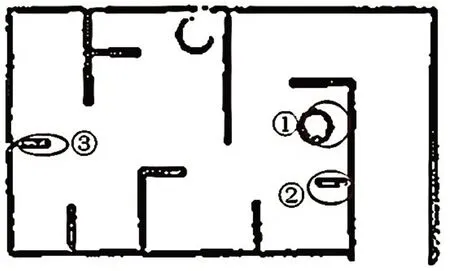
图12 优化后算法在复杂环境的建图效果

表5 3种算法在复杂环境的建图时间对比

4 结语

针对传统Gmapping算法粒子数恒定的问题，提出了一种自适应采样算法（AS），该算法可根据环境的复杂程度线性地选择采样粒子的数量。实验结果表明，优化后的算法能够提高简单环境的建图速度。此外，还将萤火虫算法（AF）融合到优化算法当中，利用萤火虫算法的高集聚能力，将采样粒子通过不断迭代的方法进行寻优操作；同时，为了防止粒子过度集聚，依据粒子权重将全部粒子划分为高相似区和低相似区，并设置迭代阀值。实验结果表明：融合优化后的算法在面临多闭环、高相似复杂环境时，在满足定位精度的前提下，建图效果得到了显著提升，平均建图时间也有所缩短。但是，该算法也有不足之处，如在面临复杂环境时，会因采样粒子数和代码复杂度增加等问题导致平均建图时间提升缓慢，后续将针对此问题作进一步的探索与研究。