具有限额约束的投资组合优化问题的量子进化算法

马宇红，孙亚娜，李兴义

(1.西北师范大学数学与统计学院，甘肃兰州 730070;2.西北师范大学学报编辑部，甘肃兰州 730070)

0 引言

投资组合优化是根据既定的目标收益和容许风险，合理配置投资资源，以分散风险、提高收益的过程，它体现了投资者的意愿，即在一定风险水平下收益最大化或在一定收益水平下风险最小化.20世纪50年代，Markowitz建立的均值-方差投资组合模型是现代证券投资组合理论的基石[1]，他认为理性投资者可以预先确定期望收益水平使风险最小化来配置自己的投资组合，也可以预先确定风险水平使期望收益最大化来配置自己的投资组合.此后，许多学者以均值-方差模型为基础，建立了一系列投资组合模型，如半方差模型[2-3]、均值绝对偏差模型[4-6]、资本定价和套利定价模型[7]等，但是，当前投资组合问题的研究多偏重模型的建立，对算法及其有效性的研究较少，理论和应用都不够深入，所以开发快速有效的优化算法在理论和应用上都是一项非常有意义的工作.

量子进化算法以量子态矢量的表达为基础，染色体采用量子比特概率幅编码方式，这种编码方式突破了经典量子比特的表示范畴，它将一个量子染色体表示为多个态的叠加，从而使量子进化算法比传统进化算法具有更好的并行计算能力；另一方面，量子进化算法利用先验信息通过量子旋转更新个体，以此取代传统进化算法中的交叉、变异操作，这样既可以简化算法的运行机制，又能有效克服算法的早熟收敛.综合来看，量子进化算法具有量子计算的高效特征，同时具有非线性优化算法的许多优点，可以极大提高算法的全局搜索能力[18].

投资组合优化模型通常具有复杂的非线性结构、超高维的决策变量和极其宽泛的决策空间[19]，使得该问题成为一个NP难问题，所以利用传统的计算方法进行求解往往是困难的.随着量子计算技术的日益成熟，凭其高效的求解效率，它开始在投资组合优化问题中得到广泛应用.2006年，须文波等[20]基于量子粒子群优化(QPSO)算法研究多阶段投资组合优化中的投资决策方法；2008年，江家宝等[21]结合QPSO算法和模拟退火(SA)算法建立了QPSO-SA算法求解多目标投资组合优化问题，并利用美国标准普尔100指数的历史数据进行验证，结果表明，QPSO-SA算法是一种高效、可靠的优化算法；2008年，李红梅[22]将Markowitz模型嵌入到多阶段投资优化模型中，分别用粒子群算法(PSO)、量子粒子群算法(QPSO)和遗传算法(GA)求解多阶段投资组合优化问题，实验结果表明，QPSO算法具有更好的全局搜索能力.

在实际的风险证券投资组合问题中，为了避免“将鸡蛋放在一个篮子里”，必须同时配置多种风险证券，并且对每种风险证券的投资额度进行限制，这就产生了限额约束的投资组合优化问题.文中致力于发展一种适宜于求解具有限额约束的投资组合优化问题的量子进化算法.首先，为了克服算法的早熟收敛，增加种群多样性，我们改进了初始量子种群的生成方式；其次，定义了新的收益风险评判准则，并以此为目标优化投资组合，平衡预期收益和承受风险；再次，设计检查修复算子，将染色体解码得到的不可行解修复为问题的可行解；最后，实证分析证明,文中设计的量子进化算法具有较好的可靠性与稳定性，能够快速有效地求解限额约束的投资组合优化问题.

1 限额约束的投资组合优化模型

1.1 限额约束的投资组合优化问题

根据Markovwitz投资理论，投资者的决策目标是获得尽可能高的收益和承受尽可能低的风险，平衡投资收益和风险这两个相互制约的目标.在经典的Markovwitz均值-方差组合优化模型中，以投资组合的期望收益率衡量投资收益，以收益率的方差衡量投资风险，其数学模型为

约束条件为

其中，M为投资风险证券的数目;xi,ri分别为证券i的投资份额和平均收益率;cov(ri,rj)为证券i和j平均收益率的协方差;μ*为预期收益率.Markovwitz均值-方差模型要求满足预期收益的前提下投资风险最小，当然，该模型也可以表述为给定风险水平下投资收益最大.

在具体的证券投资操作过程中，一方面，为了规避风险，理性投资者在任何一种证券上的投资比重都不会太高；另一方面，一种风险证券的投资比重太低也没有实际意义，反而会增加交易成本，所以明智的投资策略是对每种证券设置一个投资限额，这就是限额约束的投资组合优化问题，其数学模型可以表述为

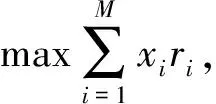
(4)

约束条件为

其中,R*为预先设定的风险水平;a>0,b<1为每种证券的投资下限和上限.以下我们记投资组合的收益P与风险R分别为

1.2 收益与风险的综合度量

在实际投资决策中，投资者往往希望其持有的投资组合同时具有较高的收益和较低的风险，然而这是矛盾的，因为高收益通常伴随着高风险，而降低风险意味着投资收益也相应减少，所以，理想的投资配置应该平衡风险与收益这两个目标.投资组合问题是一个约束优化问题，在算法设计中通常需要将其转化为无约束优化问题进行求解，尤其在群智能算法中，构造恰当的适应度函数至关重要，本文将收敛和风险两个目标整合为一个综合度量.风险是理性投资考虑的首要因素，所以在综合度量中对其赋予较大的权值；当风险满足投资者承受水平时再最大化收益.这个综合度量称为收益风险评判准则，定义为

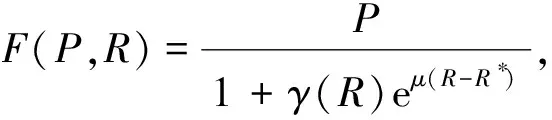
(8)

其中

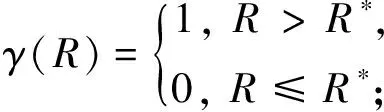
(9)

P是投资组合的实际收益;R为实际风险;R*为投资者的风险承受水平；μ是风险放大系数，其作用是放大实际风险R与风险承受水平R*之间的差异.使用这一非对称评判准则的根本原因在于：实际风险R高于风险承受水平R*是不可接受的，所以应该给予较大的惩罚项；实际风险R不超过设定风险R*时，再去放大实际收益P.

因为收益风险评判准则(8)是非线性、非连续、不可微函数，所以最速下降法、牛顿法、共轭梯度法等基于导数的优化算法并不适用，而对目标函数没有解析性要求且全局搜索能力突出的群智能算法无疑是最佳选择.文中使用(8)式作为进化算法的适应度函数，显然，当R≤R*时，F=P，此时适应度函数即为投资组合的实际收益.

2 量子进化算法

2.1 量子进化算法的基本思想

量子进化算法结合量子计算机制，它具有种群分散性好、全局搜索能力强、搜索速度快、易于与其他算法结合等优点.根据个体的编码及再生方式不同，量子进化算法分为基于旋转门的量子进化算法和基于吸引子的量子进化算法两种类型[23].

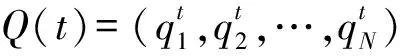
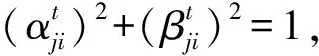
基于旋转门的量子进化算法的主要步骤包括:

4)量子更新.利用量子旋转门更新种群Q(t)中的每个个体，得到新一代种群Q(t+1)，即

这里

5)算法终止.若满足终止条件，则输出最优解x及对应的适应度F.

基于旋转门的量子进化算法采用量子编码形式，在当前最优状态的基础上，通过量子旋转对染色体的每一个量子位进行更新，以较大概率产生性能更优的下一代种群.因为采用了信息量更大的量子染色体作为种群的构造单元，使得基于旋转门的量子进化算法具有两大优势：①易于并行处理：量子染色体之间交流较少，算法并行程度较高，所以具有处理大规模数据的潜力；②鲁棒性好：量子进化算法对多个染色体同时进行搜索，而且每个染色体相对独立，所以搜索空间覆盖更完整，能够有效降低局部最优的影响，提高算法的鲁棒性[24].

2.2 改进初始种群的生成方式

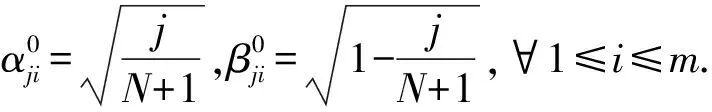
2.3 不可行解的检查修复算法

解的检查修复算法

输入：问题的解x=(x1,x2,…,xM)，投资下限a和投资上限b.

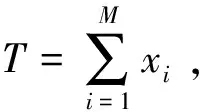
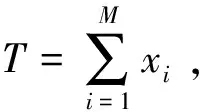
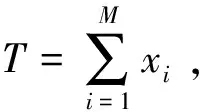
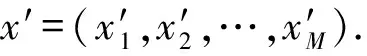
2.4 量子进化算法的基本流程

具有限额约束的投资组合优化问题的量子进化算法结合了经典量子进化算法的基本框架和解的检查修复算法，其基本流程如图1所示.

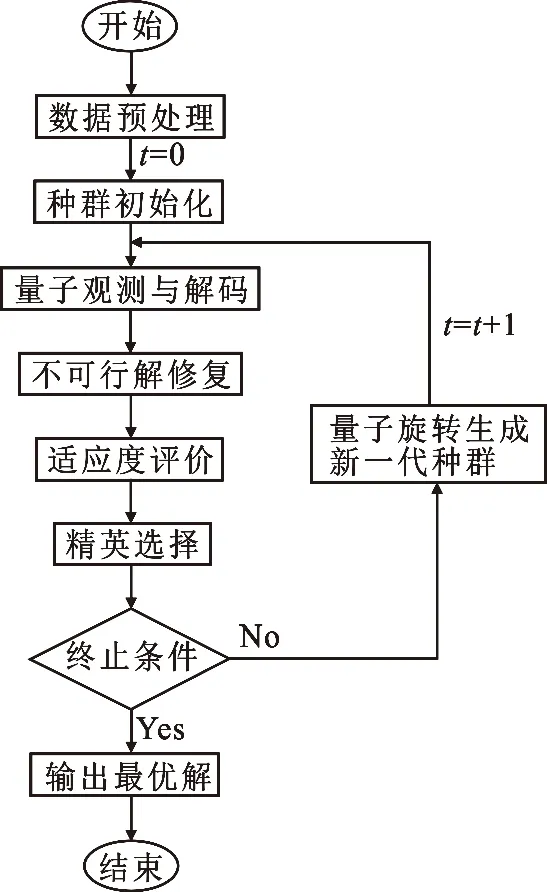
图1 算法主要流程

文中量子进化算法的主要流程如下：

1)数据预处理：导入M种风险证券在T个交易日的收益率rit(1≤i≤M,1≤t≤T)，计算每种风险证券的平均收益率ri(1≤i≤M)以及协方差矩阵σij=cov(ri,rj)，即

2)染色体编码.因为共投资M种证券，所以问题的解表示为一个M维行向量x=(x1,x2,…,xM)，每个分量使用长度为L(精度为1/2L)的量子进行编码，则一个量子染色体的完整编码为

3)初始化种群.设置初始种群Q(t)(t=0)的规模为N，则Q(t)为2N行ML列的矩阵，每2行表示一个染色体，每个染色体中长度为L的片段对应一个解分量.根据初始种群均匀分布原则，令

4)染色体观测.依次对种群Q(t)中每个染色体的量子位进行观测，得到N行ML列的观测矩阵P(t)，P(t)的每一行均为长度为ML的二进制序列.

5)染色体解码.分别对每个染色体对应的观测序列进行解码.具体操作为：依次将矩阵P(t)每行的L个元素的二进制串作为一组，将其转换成十进制数后再除以2L-1，这样L个元素的二进制串就转换为[0,1]内的实数zji(t).对每个染色体的观测序列进行解码得到N行M列矩阵X(t)，即

这里a和b分别为风险证券投资的上、下限额，xji(t)为第t代第j个染色体经解码得到的第i种风险证券的投资额度.

6)解的检查修复.N行M列矩阵X(t)的每一行对应问题的一个解，每一列对应一个投资分量，忽略进化代数t和个体序号j，我们将一个解简记为

x=(x1,x2,…,xM).

8)精英选择.比较第t代种群的最优适应度Ft与当前种群的最优适应度F，如果Ft>F，则令F=Ft,q=qt,p=pt,x=xt，否则F,q,p,x保持不变.

9)种群更新.令t=t+1，利用表1[22]规则进行量子旋转得到下一代种群Q(t).量子更新最重要的是确定旋转角度Δθ的大小和方向，Δθ值的太小，算法收敛速度将会减慢，若Δθ值太大，则算法可能发散或趋于早熟收敛，文中Δθ的值是随种群进化自适应动态调节的，其值从0.1π逐步减小到0.005π.对于某条染色体q和当前种群的最优染色体r：

记对应的观测序列分别为

y=(y1,y2,…,yML),p=(p1,p2,…,pML)

解码得到的可行解分别为

x=(x1,x2,…,xM),z=(z1,z2,…,zM)

它们对应的适应度分别为Fx,Fz，则θ的旋转方向可依据表1确定.

表1 Δθ的旋转方向

10)终止条件.若终止条件(种群进化代数)满足，则输出最优解z及其对应的适应度Fz、风险Rz和收益Pz，算法终止.

3 实证分析

3.1 算法的参数设置

文中选取上海和深圳证券交易所不同板块的25支股票随机生成5种投资组合(表2)，每种组合包含10种股票.选取每种股票从2021年6月24日至2021年9月1日共50个交易日的收益率数据进行分析.设置量子种群规模N=20，进化次数G=200，收益风险评判准则中放大系数μ=50，量子旋转角度随种群进化代数自适应进行调整，即Δθ=0.1π-t(0.1π-0.005π)/G，t为当前种群进化代数.由于每种投资组合潜在风险各不相同，因此风险承受水平R*依赖于每种投资组合的固有风险.设定投资下限a=0.05，上限b=0.3，量子染色体的编码长度为M*L=10*14.为了消除算法随机因素的影响，每种投资组合均独立运行10次然后取平均值衡量算法的性能，编程使用Matlab R2018b，运算平台为64位操作系统Intel(R)Core(TM)i7-4702MQ CPU@ 2.20GHz处理器，RAM 4GB个人电脑.

表2 5种投资组合的构成

3.2 结果与分析

图2是初始种群使用相同编码和均匀编码生成方式，不同风险水平R*下投资组合1收益率的优化进程.由图2(a)可见，初始种群中所有个体量子编码完全相同时，算法进化到60代以后，种群适应度几乎不再发生改变，算法趋于早熟收敛，陷于局部最优，当R*分别取1.2×10-4,2.0×10-4,2.8×10-4,3.6×10-4和3.9×10-4时，算法终止时最大适应度分别为1.291×10-3,2.865×10-3,3.846×10-3,4.408×10-3和4.674×10-3；由图2(b)可见，当初始种群中个体的染色体编码均匀分布时，种群的最大适应度随着进化代数的增加逐步增加，最后趋于稳定，当R*分别取1.2×10-4,2.0×10-4,2.8×10-4,3.6×10-4和3.9×10-4时，算法终止时最大适应度分别为1.308×10-3,3.366×10-3,4.083×10-3,4.605×10-3和4.748×10-3，分别增加了1.31%,17.49%,6.16%,4.47%和1.58%.

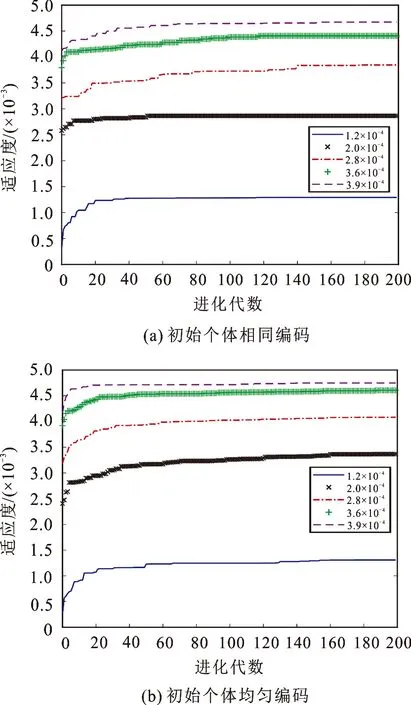
图2 不同初始种群生成方式的进化过程

为了考察风险承受水平R*与收益率P之间的关系，对不同风险水平R*，在初始种群的量子编码为均匀分布，其他参数不变的情况下独立运行10次，计算收益率的平均值P.图3显示的是这5种投资组合的有效边界，其中横坐标表示最优投资组合的实际风险R，纵坐标为收益率P.可以看出，5种投资组合的有效边界形态基本相同，高收益对应高风险，因此投资者应根据自身的风险承受水平配置投资组合，从而实现一定风险水平下预期收益最大化；或者根据自己的预期收益合理配置投资组合，实现目标收益下的风险最小化.

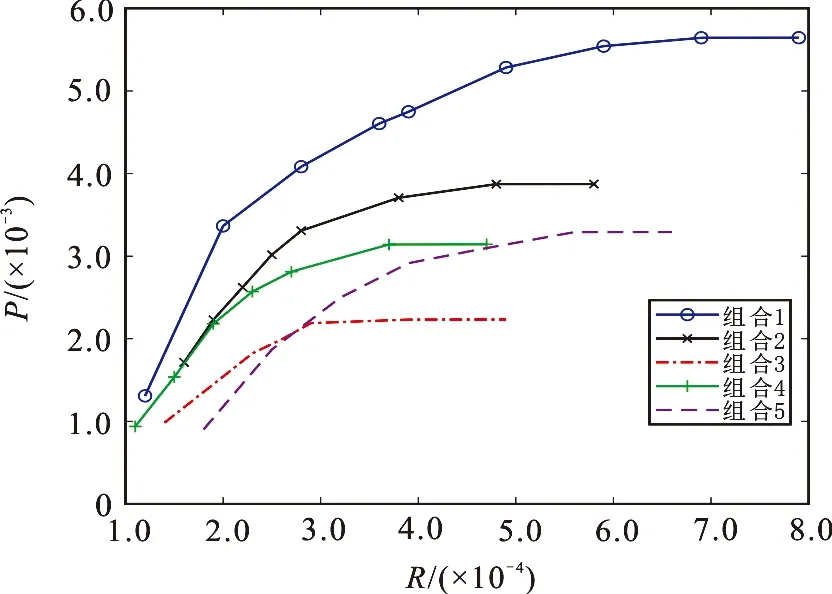
图3 收益率与风险的关系

表3为5种投资组合在不同风险水平R*下独立运行10次获得的收益率P的最大值、最小值、平均值以及标准差.从中可以看出，随着风险水平R*的增加，收益率的最大值、最小值和平均值都在增加，标准差在减小，说明随着风险水平R*的增加，量子进化算法的稳定性和可靠性更好.

表3 5种投资组合在不同风险水平R*下收益率P的 最大值、最小值、平均值和标准差

表4是5种投资组合对应不同风险水平R*的最优投资配置及其实际风险及收益率.可以看出，对于投资组合1，当风险水平从1.2×10-4逐步上升到3.9×10-4时，收益率从1.323×10-3稳步增加到4.836×10-3,并且资金逐步集中到2(13.68%),5(24.73%),7(26.48%)3种股票上,占比高达64.89%，而其余7种股票的投资比几乎均为5%，说明股票2,5,7具有高风险、高收益特征.同理，随着风险水平上升，投资组合2的资金逐步集中到2(26.09%),5(8.91%),10(30%)3种股票上，总占比65%；投资组合3的资金逐步集中到3(28.42%),5(28.97%),10(7.6%)3种股票上，总占比64.99%；投资组合4的资金逐步集中到4(15.5%),5(20.41%),6(29.1%)3种股票上，总占比65%；投资组合5的资金逐步集中在4(26.06%),8(25.87%),10(13.07%)3种股票上，总占比65%.所以对于每种投资组合来说，随着风险水平R*的增加，收益率也在逐步增加；平均收益率较高的股票其投资份额随着风险水平的增加越来越接近投资上限.这说明本文给出的限额约束投资组合优化问题的量子进化算法是合理的.

表4 5种投资组合对应不同风险水平R*的最优投资配置

4 结束语

文中将量子进化算法应用到风险证券投资组合优化问题中，给出了限额约束投资组合优化问题的数学模型，并提出了一种同时优化风险与收益的新准则，设计了解的检查修复算法；对初始种群量子编码的生成方式做了改进，增加了种群的多样性；给出了量子进化算法的流程框架，并实证求解了带有限额约束的投资组合优化问题.结果表明，本文量子进化算法能够快速有效地求解带有限额约束的证券投资组合优化问题，在相同条件下优化效果更好，收敛速度更快，稳定性更好.本文的不足之处在于我们还没有与其它成熟的经典群智能算法和量子群智能算法的性能进行比较，这也是我们下一步工作的重点.