间接信号吸收的趋化模型解的全局有界性
2022-05-16刘璐璐
辛 巧,刘璐璐,2,许 璐
(1.伊犁师范大学数学与统计学院,新疆伊宁 835000;2.新疆理工学院理学院,新疆阿克苏 843100)
0 引言
趋化现象是自然界中常见的现象,它描述的是细胞或细菌对化学信号浓度梯度的定向运动[1-3].关于直接信号吸收的生物趋化模型
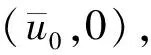
对于具有Logistic源的直接信号吸收模型
当D(u)=1时,Lankei等[7]证明了:当μ足够大时该模型存在全局经典解,当μ>0时该模型存在经典弱解;2018年,Zheng[8]证明了:当趋化敏感系数D(u)≥CD(u+1)m-1,CD>0,且
时,该模型对于任意足够光滑的初值都存在一个经典的有界解.
对于间接信号吸收的生物趋化模型
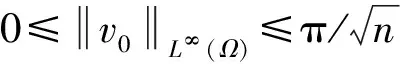
对于具有间接信号吸收的拟线性趋化模型
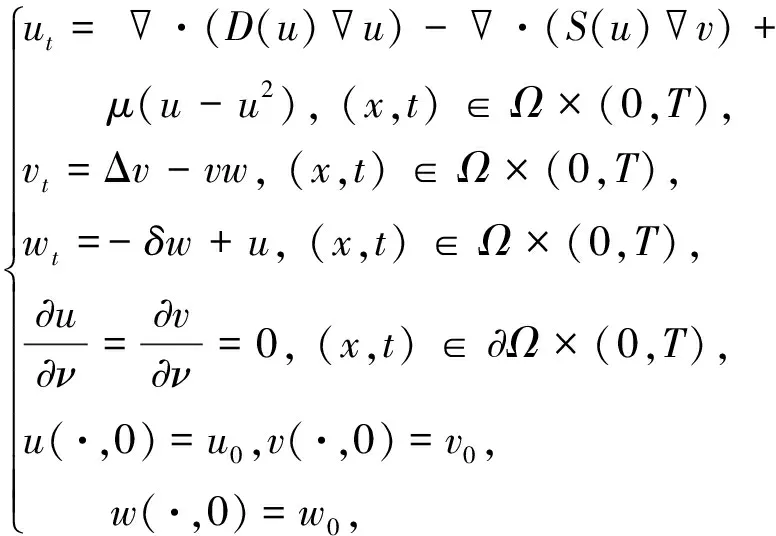
(1)
Zheng等[11]证明了:当n=2,D(u)≥um,S(u)≤uq,且m>max{1,2q-3}时,模型(1)的解全局有界.受上述文献的启发,综合文献[8,10-13]的方法,文中利用能量方法证明:若δ=1,n≥3,μ>0,且
则模型(1)的解全局有界.
文中的主要结论如下:
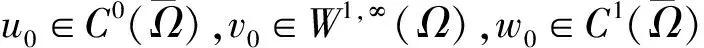
在Ω×(0,∞)上是模型(1)的经典解.当D(u)和S(u)满足条件(2),且m>max{1,2q-3},t∈(0,∞)时,存在一个常数C>0,使得
注1文献[11]在二维情况下讨论模型(1)解的有界性,文中讨论n≥3时模型(1)解的有界性.
为简单起见,对任意p>0,记Lp=Lp(Ω),L∞=L∞(Ω).
1 预备知识
引理1[7]对任意φ∈C2(Ω),n∈N,有
|Δφ|≤|D2φ|2.
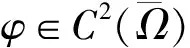
引理3[7]设n≥3,μ>0,(u,v,w)是趋化模型(1)的解,则对任意t∈(0,Tmax),有
||v(·,t)||L∞≤||v0||L∞,
且||v(·,t)||L∞随时间t单调递减.
引理4令s≥1,q≥1,假设p>0,γ∈(0,1)满足
则存在c0,c1>0,使得对任意的u∈W1,2(Ω)∩Ls/q(Ω),有
||u||Wp,2≤c0||u||u+c1||u||Ls/q.
2 解的全局有界性
为了证明定理1,先给出几个必要的引理.
引理5设m>max{1,2q-3},n≥3,μ>0,则对任意p>1,β>1,模型(1)的解(u,v,w)满足
其中
证明对趋化模型(1)的第一个方程两边同乘以up-1并在Ω上积分,则有
对(5)式右端第一项利用Young不等式和引理3可得
对(5)式右端第二项用Young不等式可得
最后联立(5)~(7)式,引理得证. 】
引理6设m>max{1,2q-3},n≥3,β>1,则对任意p>1,模型(1)的解(u,v,w)满足
证明对模型(1)的第二个方程直接进行计算,并分部积分可得
对(9)式右端利用引理1和Young不等式可得
由于
其中a∈(0,1).整理(9)~(12)式可得
对(13)式右端利用Young不等式和引理3可得
其中
最后,联立(9)~(14)式,引理得证. 】
引理7设n≥3,则对任意p>1,β>1,模型(1)的解(u,v,w)满足
证明对趋化模型(1)的第三个方程乘以wβ后运用Young不等式可得
引理8设m>max{1,2q-3},n≥3,则对任意的t∈(0,Tmax),存在一个正常数C5使得模型(1)的解(u,v,w)满足
证明令β>1,β 从而可以推出 进一步可得m>2q-3. 最后整理可得 基于以上引理,即可证明定理1. 定理1的证明首先,假设(u,v,w)是模型(1)的解,则对任意的t∈(0,Tmax),存在常数C>0,由常微分方程理论和Hölder不等式可得 又由p>n时θ∈[1,∞]可得 其中φ>-1,即可证明||v(·,t)||L∞≤C. 其次,对任意p>1,若m>max{1,2q-3},D(u)和S(u)满足条件(2),则对模型(1)的第一个方程两边同乘以up-1并在Ω上积分可得 其中m≥2q-3.整理(20)式可得 令p0>max{1,m-1},并记 对(21)式右端运用引理4可得 其中 再运用Young不等式可得 其中 整理(22)~(24)式可得 其中λ>1,t∈(0,T). 对(25)式在(0,t)上积分可得 对任意的k∈N,若 则直接可得||u(·,t)||L∞≤C.否则,直接计算 应用ln(1+z)≤z(z≥0),并对(26)式两端求pk次根可得到||u(·,t)||L∞≤C. 最后,对模型(1)的第三个方程求一阶线性常微分方程的解,显然可得 ||w(·,t)||L∞≤C. 从而定理1得证.】