考虑炸高和相位角影响的射孔枪卡枪及强度流固耦合分析

窦益华，朱晓栋，范永均,2，李明飞

(1.西安石油大学 机械工程学院，西安 710065;2.中国石油西部钻探工程有限公司，乌鲁木齐 830000)

随着石油工程技术的发展，射孔完井工艺不断追求深穿透、高孔密射孔，射孔弹的装药量和装药密度不断增加，射孔高爆轰能量下将增加射孔枪的毛刺高度和应力，常引起卡枪、损坏等安全事故。井下射孔工况复杂，试验困难，现有研究大多采用ANSYS/LS-DYNA软件模拟，但是对于强爆轰下的流固耦合，存在网格比例失调导致的分析意外终止、设置缺失引起的速度超限和计算机时过长等问题。因此，有必要在有效解决上述问题的基础上，研究炸高和相位角对射孔枪毛刺和应力的影响，避免射孔卡枪和损坏事故。

射流侵彻将在射孔枪内外壁造成毛刺，并在孔间区域产生应力叠加，容易造成卡枪和应力超限事故，理论和试验分析困难，常采用数值方法分析，但对于高爆轰下的流固耦合，存在很难克服的问题，需要开展针对性研究。文献[1]应用AUTODYN软件模拟了半球结构装药流固耦合对靶板的毁伤。文献[2]应用LS-DYNA软件模拟了聚能射流形成过程，研究了射流的速度变化。文献[3]应用Workbench模块，建立射孔段管柱三维有限元模型，分析了管柱的动力响应规律。文献[4]用AUTODYN软件研究了射孔弹爆轰压垮药型罩过程和射流侵彻套管过程，但只研究速度与能量变化，未分析毛刺和应力。文献[5]模拟与试验结合验证聚能射流对不同抗拉强度、抗压强度水泥的影响。文献[6]研究了影响射孔枪稳定性能的因素，如：枪长、温度、载荷等。文献[7]用LS-DYNA软件模拟了不同装药结构对射流形成的影响，为本文模型的建立及相关参数的选取提供借鉴。文献[8]研究了不同药形罩锥角对射流的影响，为本文药形罩模型的建立提供了思路。文献[9]模拟了不同相位角射孔对射孔枪抗外挤强度的影响，找出最佳相位角为60°。文献[10]依据圆柱壳开小孔弹塑性力学理论，得出应力集中系数，计算出了整个圆孔周围应力分布，找到应力集中最大点。文献[11]模拟了不同炸高对侵彻深度的影响，为本文提供有益思路。文献[12]用LS-DYNA软件研究了射流侵彻砂岩时裂缝形成机理。文献[13]研究了砂岩地应力对射流孔径及穿深的影响，垂直于射孔方向的地应力影响更大。文献[14]研究了不同孔密和相位角对射孔枪抗压强度的影响。文献[15]用LS-DYNA软件研究了聚能射流射孔枪毛刺影响，但模型未考虑射孔液及砂岩，模型建立不完整。

综上所述，现有LS-DYNA二维仿真分析较多，三维模型往往建立不完整，分析中还存在意外终止、速度溢出和计算时长等问题。本文用LS-DYNA软件，建立射孔弹-射孔枪-射孔液-套管-砂岩三维有限元模型，严格控制各部分单元体尺寸比例，避免分析意外终止；合理设置限制最大时间步长的LCTM曲线，解决速度超限问题。通过设置网格渐变、添加对称约束，大幅降低机时，探究炸高和相位角对射孔枪毛刺和应力的影响机理，可为射孔爆轰侵彻类问题研究提供思路。

1 射孔枪流动应力与塑性应变方程

本构方程表征金属发生塑性变形时流动应力与应变之间的关系[16]，聚能射流侵彻射孔枪时，射孔枪会发生大塑性变形，其流动应力表达式为

(1)

塑性应变方程为

(2)

(3)

(4)

综合式(1)和式(2)，得到射孔枪Johnson-Cook模型的本构方程为式(5)，该模型适用于大应变、高应变率、高温环境

(5)

式中:C为剪切-压缩波速度(Vs-Vp)曲线的截距；S1、S2、S3为(Vs-Vp)曲线的斜率；γ0为状态方程常数，γ0=1.51；a为γ0一阶体积正量。

2 单枚弹时射孔枪应力变化规律分析

炸药爆轰压垮药形罩形成射流侵彻射孔枪时，射孔枪发生塑性变形，孔道周围材料堆积、外翻形成毛刺，引发卡枪事故，同时射孔枪应力急剧增加，超过材料屈服极限，常引发安全事故，因此，有必要研究射流侵彻时射孔枪的毛刺和应力变化规律。

2.1 参数选取及常见问题解决

以大庆某油田井下3 500 m射孔过程为研究对象，用LS-DYNA软件建立射孔弹-射孔枪-射孔液-套管-砂岩三维有限元模型，射孔弹采用HS46射孔弹，药形罩为高导无氧铜，炸药为RDX，射孔枪采用32CrMo4，套管采用P110材料，射孔液由清洁淡水中加入盐等少量添加剂配制而成，射孔液的材料模型和状态方程分别采用Null和Gruneisen。具体参数见表1。

表1 三维建模关键参数

聚能射流仿真中容易出现计算意外终止的问题，常由药形罩网格比例失调和畸变引起，为了提高网格质量，先划分面网格，然后旋转生成体网格。划分射孔弹面网格时，需保证药形罩、炸药、弹壳的面网格份数大致相同，保证体网格各部分之间的网格大小和数量成比例，尽量减少空气域的网格数量，以解决网格畸变、计算意外终止的问题；速度超限问题常由材料参数设置不当引起，因此在设置时，需添加最大时间步长曲线，限制射流侵彻步长；针对计算机时过长问题，如图1和图2所示。①设置对称约束的1/4模型代替完整模型；②合理设置射孔枪、套管和砂岩网格的渐变，大幅降低计算时间。

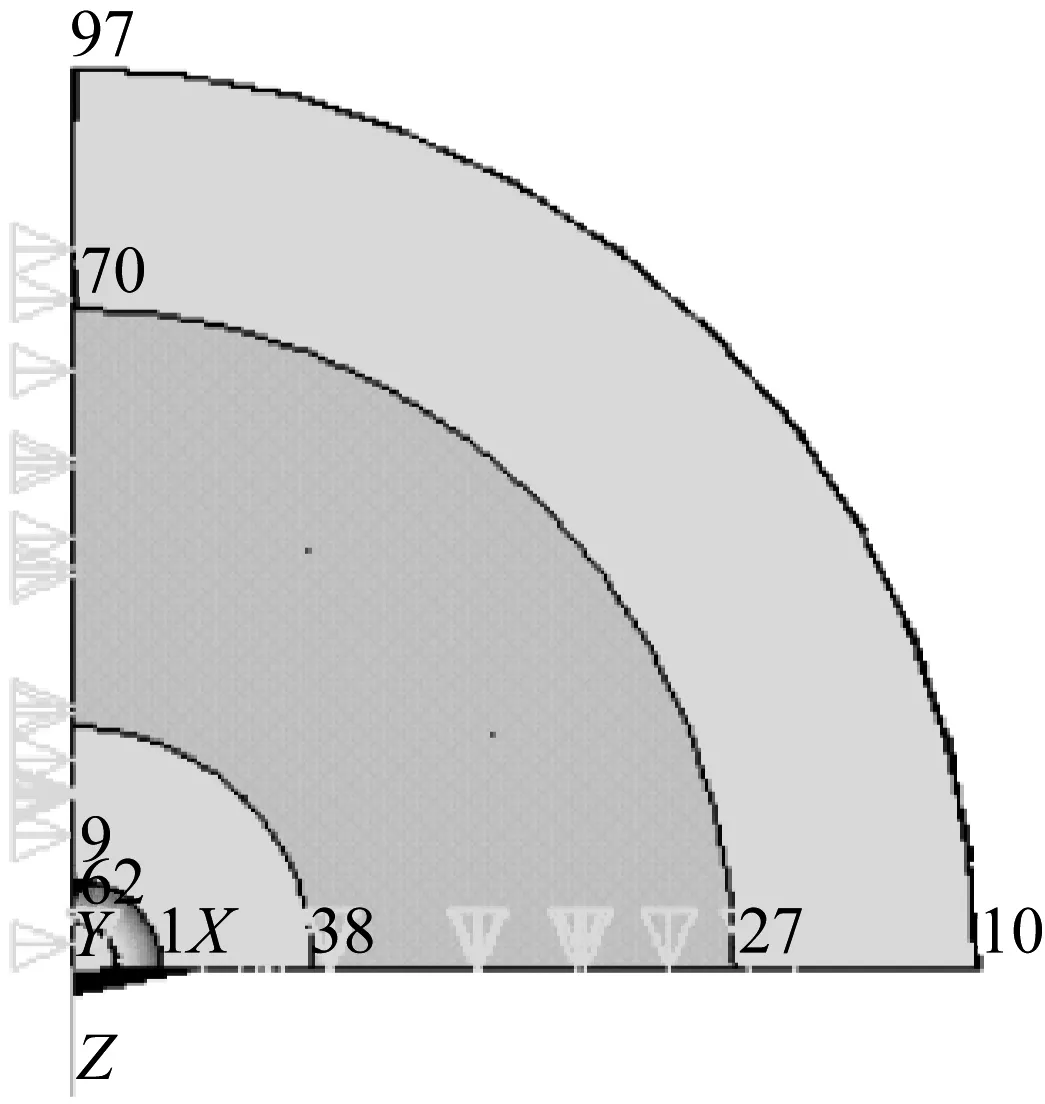
图1 射孔弹对称约束(μm)

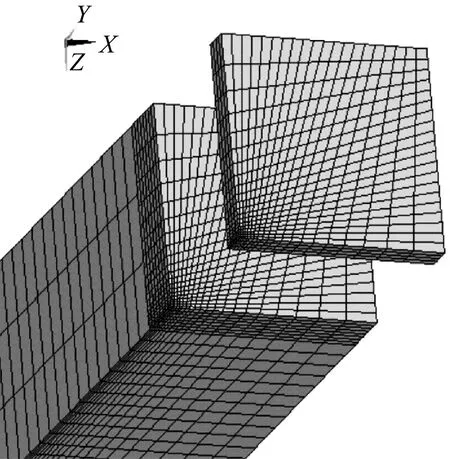
图2 渐变线及网格

2.2 单枚弹不同炸高对射孔枪毛刺影响分析

超高速金属射流侵彻射孔枪时，射孔枪内射流侵彻区域应力迅速增大，超过材料的屈服极限使得射孔枪发生塑性变形，孔道周围材料向孔边堆积外翻，形成毛刺。毛刺形成大致分为3个阶段：①射流穿过射孔枪时，射孔枪发生塑变，孔道周围材料外翻形成毛刺；②射流杵体开始侵彻射孔枪时毛刺进一步加大；③药形罩尾部挂枪量作用于射孔枪，使毛刺进一步增大(注：药形罩尾部由于工艺原因常与炸药对接，使得尾部药形罩不能充分形成射流，从而挂在射孔枪上，简称药形罩挂枪量)。分别建立炸高为12 mm、18 mm、24 mm的有限元模型，分析不同炸高对毛刺高度的影响，射孔枪最大毛刺示意图如图3所示。药形罩挂枪量对毛刺影响的示意图如图4所示。

图3 射孔枪最大毛刺

图4 挂枪量对毛刺的影响

炸高12 mm时，射孔枪毛刺示意图,如图5(a)所示。药形罩从被压垮形成射流到侵彻射孔枪距离较小，射流头部直径大，射孔枪毛刺变化规律图如图5(b)所示。16 μs时，射流头部穿过射孔枪，射孔枪外壁明显外凸形成毛刺，头部后的射流直径较小，因此，头部后的射流穿过时毛刺高度不变；20 μs时，杵体侵彻射孔枪，与孔边材料摩擦带动毛刺迅速增大，55 μs时，杵体前部侵彻射孔枪完成，此时挂枪量附着并作用在射孔枪上，使毛刺高度进一步增大，75 μs时，毛刺高度达到最大值4.1 mm，之后不再发生变化。图6所示为炸高18 mm时毛刺的变化规律图，整体变化规律与炸高12 mm时相近，不再进行详细分析，射孔枪毛刺高度在80 μs时达到3.9 mm。图7(a)为炸高24 mm时，射孔枪毛刺示意图，射流头部直径相对炸高为12 mm时较小，射流尾部直径较大；图7(b)为毛刺变化规律图，19 μs时，射流侵彻射孔枪形成毛刺，开始时毛刺高度缓慢增加；36 μs时，射流杵体穿过射孔枪，毛刺迅速增大；60 μs时,毛刺高度在药形罩挂枪量作用下继续缓慢增大，最大毛刺在80 μs时达到3.6 mm。

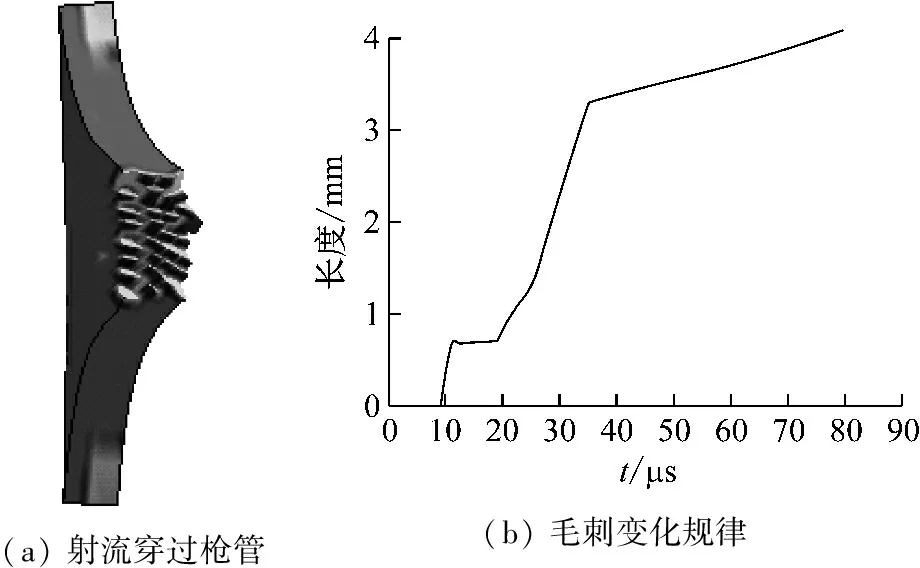
图5 炸高12 mm毛刺变化图

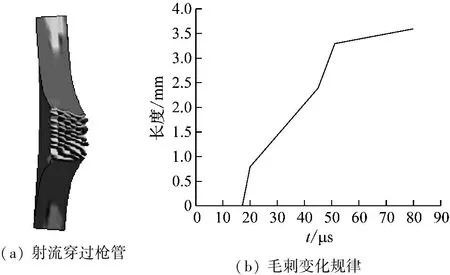
图6 炸高18 mm毛刺变化图

图7 炸高24 mm毛刺变化图

2.3 单枚弹不同炸高对射孔枪应力影响分析

炸高12 mm时的射孔枪应力云图如图8所示。图8中穿过中心的圆周代表应力超过材料屈服极限(见图8(a))。38 μs时，射孔枪应力达到最大值1 075 MPa，此时孔道周围55 mm的圆周内，应力均超过材料屈服极限835 MPa，超过材料屈服极限后，射孔枪材料强度下降、脆性增强，不再遵循射孔枪材料的性能曲线。之后随着射流继续侵彻，射孔枪最大应力值不断下降，但超过材料屈服极限的应力圆周继续增大，112 μs时，应力圆周直径达到61 mm，之后应力圆周直径不断变小，射流杵体完全穿过射孔枪后应力开始下降(见图8(b))。

(a)38 μs

炸高为18 mm时，单枚射孔弹侵彻射孔枪的应力变化云图如图9所示。射流开始侵彻射孔枪时，射孔枪应力逐渐增大；17 μs时，射流开始在射孔枪扩孔，此时孔道周围2 mm的圆周内应力均超过射孔枪材料的屈服极限，此时的最大应力为850 MPa；18 μs时，射流侵彻穿过射孔枪，孔道周围应力圆周不断增大，直径达到6 mm；19 μs时，孔道周围超过屈服极限的应力圆周直径达到最大值约9 mm，此时射孔枪最大应力为946 MPa；54 μs时，射流杵体开始侵彻射孔枪，射孔枪应力继续增大，最大值达到997 MPa，孔道周围超过材料屈服极限的应力圆周直径达到45 mm，材料塑性变形不断增大，之后应力圆周的直径维持30 μs左右不变后开始逐渐变小(见图9(a))。113 μs时，杵体不再向前运动，射孔枪应力开始下降。炸高为24 mm时，射孔枪的应力在42 μs时达到最大值912 MPa，此时超过材料屈服极限的应力圆周直径为38 mm，之后射孔枪内的最大应力和超过材料屈服极限的应力圆周直径均不断下降(见图9(b))。

图9 单枚弹射孔枪应力云图

3 不同相位角对射孔枪应力变化影响分析

考察了不同相位角下毛刺的变化情况，与单枚时变化不大，篇幅限制，不再赘述。主要考察相位角对射孔枪应力的影响规律。

3.1 相位角为30°时射孔枪应力变化规律

16孔/m、相位角30°时，两枚射孔弹的应力变化云图如图10所示。11 μs时，射流头部侵彻射孔枪内壁(见图10(a))。14 μs时，射流穿过射孔枪，此时，超过材料屈服极限的应力圆周直径为3 mm(见图10(b))。之后两孔周围的应力圆周不断增大，54 μs时，两孔间应力圆周重叠，最大应力835 MPa(见图10(c))。78 μs时，射流杵体侵彻射孔枪，此时最大应力在两孔连线中间约为1 226 MPa，超过材料屈服极限的应力圆周的直径达到55 mm(见图10(d))。

图10 两枚弹射孔枪应力云图

3.2 相位角为60°和90°时射孔枪应力变化规律

16孔/m，相位角为60°时，两枚射孔弹的应力云图，如图11所示。14 μs时，射流头部侵彻射孔枪内壁(见图11(a))；17 μs时，射流对射孔枪侵彻完成，由于爆轰能量叠加作用，射流侵彻穿过射孔枪较单枚弹时提前1 μs，射孔枪最大应力提高154 MPa(见图11(b))；29 μs时，两枚射孔弹的应力叠加，此时应力作用范围达到35 mm(见图11(c));65 μs时，两枚射孔弹的应力重合，此时，最大应力圆周直径达到最大值，呈现不规则状态，距离孔边距离约为42 mm，最大应力达到1 214 MPa(见图11(d))；110 μs时，射流杵体停止运动，应力逐渐下降。图12所示为相位角90°时射孔枪应力云图，29 μs时，超过材料屈服极限的应力圆周重叠，69 μs时，超过材料屈服极限的应力区域距离孔边66 mm，射孔枪的应力达到最大值1 221 MPa，较相位角60°时的最大应力提高了7 MPa。

(a)14 μs应力云图

(a)50 μs应力云图

4 结 论

本文应用LS-DYNA软件，建立射孔弹-射孔枪-射孔液-套管-砂岩三维完整模型，研究炸高和相位角对射孔枪卡枪及应力强度的影响，得出以下结论：

(1)炸高为12 mm时，射孔枪毛刺为4.1 mm，最大应力1 075 MPa；炸高为18 mm时，射孔枪毛刺为3.9 mm，最大应力997 MPa；炸高为24 mm时，射孔枪毛刺为3.6 mm，最大应力912 MPa，射孔枪最大毛刺和最大应力随着炸高的增加而减小。

(2)相位角为30°、60°、90°时，射孔枪的毛刺未发生明显变化，即相位角对射孔枪毛刺影响较小；最大应力分别为1 226 MPa、1 214 MPa、1 221 MPa，超过材料屈服屈服极限的应力区域分别为55 mm、42 mm、66 mm，此区域内，在高爆轰压力下，射孔枪将发生向外鼓胀，即所谓的“胀枪”，引起卡枪事故，所以相位角60°时射孔枪的强度安全性更好。