高耸烟囱风致振动的TPIMS减振数值分析
2022-05-16刘仰昭戴靠山丁志斌尹业先
杨 涵,刘仰昭,戴靠山,2,3,丁志斌,尹业先
(1.四川大学 土木工程系,成都 610065; 2.深地科学与工程教育部重点实验室,成都 610065;3.破坏力学与防灾减灾四川省重点实验室,成都 610065; 4.山东电力建设第三工程公司,青岛 266100)
高耸烟囱作为一种典型细长结构,其刚度小、阻尼低,在风荷载作用下会产生明显的风致振动。而对于圆形断面结构,涡激共振和抖振的影响最为关键[1]。
涡激共振是高柔结构在低风速下常会出现的一种带有自激性质的风致限幅振动[2]。Tamura等[3]提出了一种数学模型,较准确地预测了二维圆柱形断面在均匀流下的涡振响应;梁枢果等[4]通过风洞试验研究了基于连续气弹模型的烟囱风致响应,较好地模拟了实际工程工况。但是目前三维结构涡振响应的预测大都通过风洞试验进行,并没有一种较高效的理论方法。抖振是指高柔结构在紊流场作用下的随机振动,在部分形式类似的高耸结构中已有大量研究。丁幼亮等[5]分析了多塔斜拉桥风致抖振响应,计算了黏滞阻尼器的控制效果;周亚栋等[6]通过ANSYS模拟了大跨斜拉桥桥塔施工阶段的风致振动响应,并进行了模型风洞试验;邓洪洲等[7]推导了高耸桅杆结构风振系数,对比新旧荷载规范的差别。
对于高耸结构的风致振动,可以通过安装阻尼器的方式加以控制。由于风荷载主要激发烟囱的一阶振型[8],为了更高效地控制位移,一般会将阻尼器安装在结构顶部。传统调谐质量阻尼器(tuned mass damper,TMD)对高耸结构在风荷载作用下的响应控制,目前已有大量研究:Den Hartog[9]推导了单自由度下的TMD最优参数,即Den Hartog公式;Warburton[10]探究了TMD参数对主体结构的影响规律,并推导了TMD在不同荷载工况下的最优参数;陈鑫等[11]设计了环形TMD等装置,推导其力学模型。但是,对于传统的TMD,其最大问题是为了达到设计减振效果,通常需要非常大的质量[12],增加主体结构负担,提高了工程造价。惯容阻尼器是一种利用惯容原理制作的阻尼器,通过惯容器的质量增大效应提供更大的惯性力,可以在保证减振能力的基础上,有效降低阻尼器的自重。目前,张瑞甫等[13-14]设计了惯容减振系统(tuned parallel inerter mass system, TPIMS)并应用在风电塔等高耸结构中。
本文以某216.5 m高的烟囱为研究对象,提出了一种可预测三维烟囱在均匀流下涡振响应的方法,并通过连续随机离散流技术(consistent discrete random inflow generation,CDRFG)[15]模拟了紊流风场。采用ANSYS分别计算烟囱的涡激共振与抖振响应,并分别利用TMD和TPIMS进行振动控制,对两者的风致振动位移减振率进行了对比分析。
1 工程背景与计算方法
1.1 工程背景
某工业烟囱高216.5 m,质量约15 000 t,圆形断面,外筒为钢筋混凝土结构,其材料力学性能参数如表1所示。底部外径为24 m,至110 m标高处变为18.2 m;在180 m标高处变为18.3 m直至顶部。底部的壁厚为65 cm,顶部为35 cm,最薄处30 cm。在标高205 m处设置支撑平台以固定内外筒。烟囱模型示意图如图1(a)所示。

表1 烟囱外筒材料力学性能参数表
在ANSYS中使用梁单元(Beam4)模拟烟囱,按一定高度分为若干段,每一段视为一根短梁。将材料的密度设为0,并通过在节点处添加质量点的方式添加自重。将内筒的支撑平台看作一个质点放在205 m高处,把内筒的全部质量放在支撑平台上。对这一模型做模态分析,并绘制其第一阶模态振型,如图1(b)所示。经计算,该模型的X方向一阶自振频率为0.330 2 Hz,与同结构SAP2000壳单元模型的0.316 Hz差距约为4.5%;Y方向一阶自振频率为0.339 71 Hz,与壳单元的0.332 Hz差距约为2.3%,均小于一般工程要求的5%误差。可见该梁单元模型能较好模拟实际结构。另一方面,本研究为尽可能在数值模拟阶段发现结构可能存在的安全风险,计算时将结构的阻尼比调小取为0.5%,以获得偏危险的结果,确保结构在实际工程环境下的安全性。

(a)烟囱外形
1.2 风致振动介绍
1.2.1 涡激共振
(1)二维平面内涡激共振
涡激共振是工程领域中常见的流固耦合现象之一[16]。Tamura通过建立数学模型得出了圆形断面在均匀流下的涡振响应无量纲位移方程,即
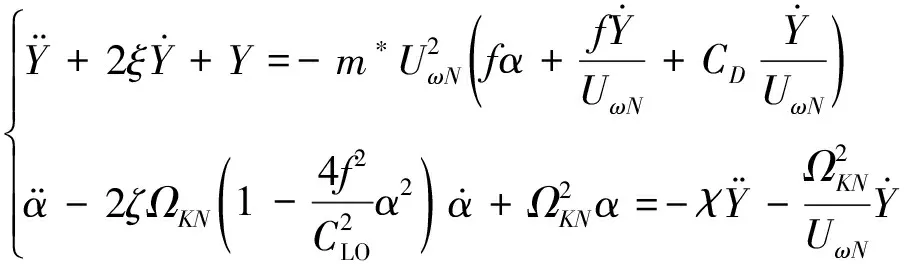
(1)

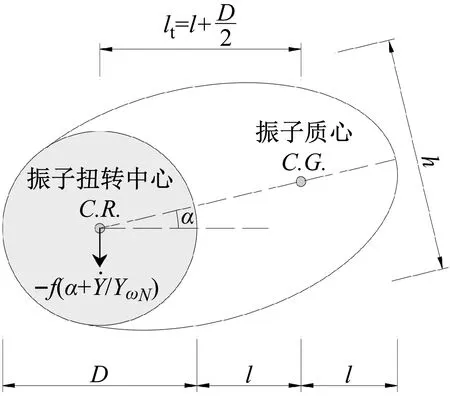
图2 尾流振子模型示意图
解方程组式(1),可推导出断面处的有效涡激力系数(即只考虑气动阻尼效应而忽略气动刚度效应的涡激力作用系数)幅值CYO[17]
(2)
(2)三维风场下的涡激共振
式(2)仅适用于二维的圆柱,对于三维烟囱结构,需要考虑其模态振型。另外,风速沿z方向(高度方向)的变化也应考虑在内,如图3所示。因此,有
(3)
Y(z,t)=φ(z)·q(t)
(4)
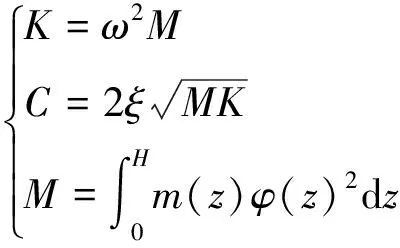
(5)
式中:v(z)指高度为z处的风速;vR为参考高度处的风速;zR为参考高度;γ为地面粗糙度指数;Y(z,t)为t时刻下高度为z处的无量纲位移;φ(z)为结构一阶模态振型;q(t)为第一阶振型广义坐标;m(z)指高度为z处的烟囱单位长度质量;H为结构高度;M为模态质量;K为模态刚度;C为模态阻尼。三维烟囱在均匀流下的涡振响应示意图如图3所示。
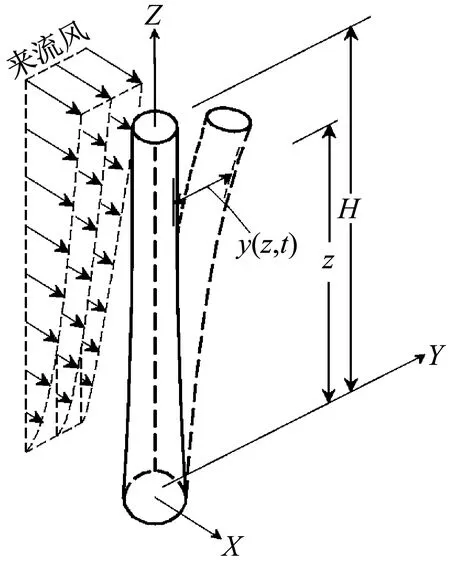
图3 三维烟囱涡振响应示意图
于是,一阶模态下结构的运动方程为:
(6)
根据式(2)得到的有效涡激力系数CYO,可得高度为z处烟囱单位长度所受的横风向涡激力为
(7)
沿z方向积分,同时考虑结构的模态振型,有
(8)
联立式(6)与式(8),有
(9)

图4 基于有限元的迭代法流程
步骤2对于每一个确定的风速,假定其顶部无量纲振幅Yts。
步骤3通过结构的一阶模态振型计算出各节点的假定无量纲振幅,从表中查找每个节点对应的CYO值。
步骤4由式(2)~式(7)计算所有节点的涡激荷载时程,导入ANSYS中计算模型实际顶部无量纲振幅Ytc,并与Yts对比。
步骤5如果Ytc与Yts的误差小于设定阈值,则认为找到此风速下烟囱的涡振振幅的一个解(由于“迟滞”现象的存在,部分风速下可能出现超过多个解的情况),继续寻找下一个风速的涡振振幅,否则重复步骤2~步骤4。
对于迭代法,需要验证其正确性。此处通过与风洞试验结果和Runge-Kutta法结果对比验证。关于圆柱在均匀流下的涡振响应,已有大量学者做过风洞试验,其中Feng[18]的试验最经典。建立与Feng基本结构参数相同(m=0.949 kg,k=4.1 N/m,c=0.004 1 kg/s)的弹性支承梁,分别用Runge-Kutta方法与迭代法计算响应,并将无量纲振幅与无量纲风速的关系绘制成图形,如图5所示。

图5 两种方法计算结果与风洞试验数据对比
从图5可知,两种理论计算方法的结果与风洞试验结果在涡振振幅峰值处的无量纲位移及对应的无量纲风速非常接近,表明迭代法可以计算烟囱在涡激荷载下的峰值响应并评估阻尼器的减振效果。由于迭代法忽略了气动刚度的影响,与考虑气动刚度影响的Runge-Kutta方法计算结果存在一些差距。同时,由于Tamura尾流振子模型忽略了涡激共振气动力中具有强迫性质的部分而只考虑了具有自激性质的部分,故两种理论方法与风洞试验之间存在一定差别。Staubli[19]指出,在涡振锁定区间中部,具有自激性质的气动激励部分影响很大,具有强迫性质的部分影响较小,两者位移差别也较小;而在涡振锁定区间边缘,具有强迫性质的气动激励部分影响有所增大,导致两者位移有所差别。另一方面,由于尾流振子模型中各经验参数的精确确定需要通过测力试验与流体可视化试验的联合测试实现,整个过程复杂繁琐,故本次采用Tamura给出的建议取值,该值与Feng试验的实际值有所区别,这是迭代法计算结果与风洞试验结果存在差距的主要原因。
使用迭代法计算烟囱顶部涡振响应随10 m高度处无量纲风速变化的关系,并拟合出烟囱的涡振曲线,如图6所示。经过计算对比,烟囱在无量纲风速约为0.59(对应实际风速22.4 m/s)时涡振响应最大,后文研究中取此时的涡激荷载作为结构的外荷载进行参数对比。

图6 烟囱顶部位移的涡振响应曲线
1.2.2 抖 振
要在时域内计算烟囱的抖振响应,首先需要模拟紊流风场。利用CDRFG,按照给定的场地条件生成烟囱塔身不同高度处的风速时程曲线。根据业主建业的规范规定,烟囱所在场地为其规定的D类场地[20],地面粗糙度指数为1/9,参考高度(10 m)处的基本风速为57 m/s(10 min平均值),名义湍流度为0.15,湍流度高度指数为-1/6,湍流积分长度尺度为198.12 m,沿长度尺度的变化指数为1/8。根据场地条件,脉动风功率谱的目标谱定为von Karman谱。同时,为了充分观察烟囱在脉动风荷载作用下的响应情况,减小偶然性,共计生成了600 s的脉动风速时程。顺风向参考高度处与烟囱顶端前100 s的时程如图7所示。横风向参考高度处与烟囱顶端前100 s的时程如图8所示。

(a)参考高度处

(a)参考高度处
生成风速时程曲线后,对这4条时程分别绘制其功率谱曲线,并与目标谱对比,如图9与图10所示。生成的功率谱与目标谱吻合良好。
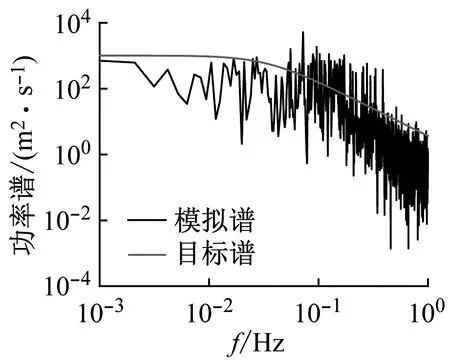
(a)参考高度处

(a)参考高度处
根据Davenport准定常抖振力模型,烟囱在随机风荷载的作用下,其受到的顺风向与横风向抖振力可用式(10)、式(11)表示
(10)
(11)
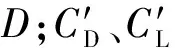

图11 顺风向与横风向抖振位移时程对比
从图11可知,相比横风向抖振响应,顺风向抖振响应更大,对结构的风致内力也更大,因此为保证结构在强风下的安全性,本文采用顺风向抖振荷载作为抖振外荷载来计算位移响应与阻尼器减振效果。
1.3 两种阻尼器模型的建立
在ANSYS有限元软件中,对于传统TMD模型,通过COMBIN14单元模拟弹簧与阻尼器、MASS21单元模拟质量块的方式实现,如图12(a)所示。TPIMS的连接方式如图12(b)所示。图12中:mt与kt分别为质量块质量与弹簧(TPIMS主弹簧)刚度;ks为TPIMS小弹簧刚度;min为惯容器表观质量;Cd为黏滞阻尼器阻尼系数。对于此系统,主要通过μt、μk和μin3个参数决定阻尼器各元器件的性能。其中,μt为质量块质量mt与结构模态质量mT的比值,μk为TPIMS自振频率ωT与结构固有圆频率ωN的比值,μin为惯容器表观质量min与质量块质量mt的比值。

(a)TMD连接方式
张瑞甫等提出在通用有限元软件中可以通过现有元器件等效的方式模拟惯容器。采用等效方式模拟TPIMS的原理如图13所示。图13中:mi为第i个质点质量,θi为梁单元在该点处的转角。

图13 TPIMS系统建模示意图
惯容器的核心特点是拥有比自身物理质量大得多的表观质量,通过设置圆盘的转动惯量与质量,将圆盘与杆件的组合等效为广义的惯容器。圆盘的表观质量由式(12)确定
(12)
式中:J为圆盘的转动惯量;l为刚性杆的长度。
为了让两种阻尼器均能充分发挥效果,同时考虑到实际工程中安装的可行性,将阻尼器放置于210 m高度处。烟囱安装两种阻尼器后的有限元仿真模型,如图14所示。

(a)TMD控制模型
2 涡激振动下两种阻尼器减振效果分析
2.1 阻尼器参数取值
对于基本接近于简谐形式的涡激荷载作用下TMD的刚度和阻尼的最优取值,可由式(13)、式(14)确定
(13)
(14)
考虑到实际工程的可行性和烟囱设计时的承载能力,此处阻尼器的质量块分别取10 t、34 t和102 t,对应模态质量比分别为0.3%、1%和3%,以对比不同质量比下TMD减振效率的变化。将对应的μ代入式(13)、式(14)即可计算出3种质量比对应的TMD自振频率和阻尼比。
对于TPIMS减振系统,使用遗传算法取出最优参数。在设定质量比为0.3%的条件下,将减振效率设置为优化目标,最终得到参数为:uin=0.147 25、uk=0.998 1、κ=0.010 989、ξ=0.710 13。
由于本文主要探究不同系统的减振效果,因此涡激荷载只取无量纲位移最大处的值,即当风速为23 m/s(对应无量纲风速0.58)、顶部振幅1.64 m(对应无量纲振幅0.089)时的荷载。同样,为了使结构的振动尽可能接近稳定值并减小计算时间,取时间步长为0.01 s,共计算800 s,并取最后50 s的峰值作为迭代法的计算振幅。
2.2 减振效果对比
分别计算无控结构、3种模态质量比的TMD控制的结构与0.3%模态质量比TPIMS控制的结构的涡激振动响应,结果如图15所示。从图15可知,对于接近简谐形式的涡激荷载,无论TMD还是TPIMS都能对烟囱顶部位移起到很好的控制作用。对比两者减振率,可以看出经过遗传算法优化的TPIMS系统能够做到在0.3%的模态质量比下减振率远高于同质量比下的TMD,甚至超过3%的TMD,表明使用TPIMS系统能够明显降低自重,大幅降低造价。

图15 不同减振系统涡激荷载减振效率对比
3 抖振下两种阻尼器减振效果分析
3.1 阻尼器参数确定
对于随机荷载作用下TMD参数的取值,可通过遗传算法优化得出。惯容减振系统的参数则由改进的定点理论确定。根据这一理论,弹簧刚度比κ与阻尼器的阻尼比ξ可用TPIMS惯容质量比μin表示为
(15)
(16)
其他参数的取值如式(17)所示。通过参数优化,可得TPIMS系统的最优参数。
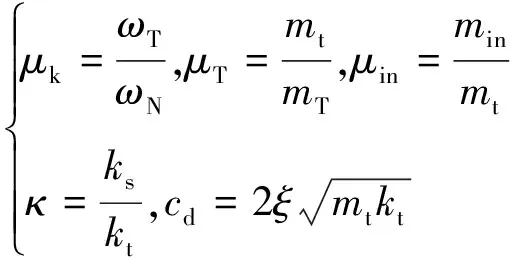
(17)
3.2 减振效果对比
分别计算无控结构、3种模态质量比的TMD控制的结构与0.3%模态质量比TPIMS控制的结构的抖振响应。其中,结构在无控制、0.3%TMD控制与0.3%TPIMS控制时烟囱顶部位移时程曲线如图16所示,将所有工况的结果绘制成柱状图,如图17所示。

图16 脉动风荷载下安装不同减振系统顶部抖振位移时程

图17 不同系统脉动风荷载减振效率对比图
从图17可知,无论是哪一种类型的减振系统,都能对烟囱在随机风荷载作用下的位移响应起到较好的控制效果。其中,在同为0.3%的模态质量比下,TPIMS的减振率相比于TMD系统有着较大的优势;在相同减振率下,模态质量比0.3%的TPIMS减振性能超过模态质量比3%的TMD,TPIMS对比TMD能显著降低减振系统质量。
4 惯容减振系统在实际工程中的问题
计算过程中发现:对于惯容减振系统,若要使其减振效果较为理想,就需要降低小弹簧的刚度ks,导致质点的相对位移较大。不同弹簧刚度比κ下TPIMS减振系统在随机荷载下的减振效率如图18所示,质点相对塔顶与小弹簧两端的相对位移如图19所示。

图18 不同κ值TPIMS在随机荷载下的减振效率对比图

图19 不同κ值TPIMS在随机荷载下的相对位移对比图
从图18和图19可知,在随机荷载作用下,当κ值增大,即小弹簧刚度ks增大时,TPIMS系统的质点相对位移有了一定程度的控制,但其减振效率也随之下降。
另一方面,TPIMS系统的阻尼比ξ也会影响系统的减振率和质点的相对位移。不同阻尼比ξ下TPIMS减振系统在随机荷载下的减振效率如图20所示。质点相对塔顶与小弹簧两端的相对位移如图21所示。

图20 不同ξ值TPIMS在随机荷载下的减振效率对比图
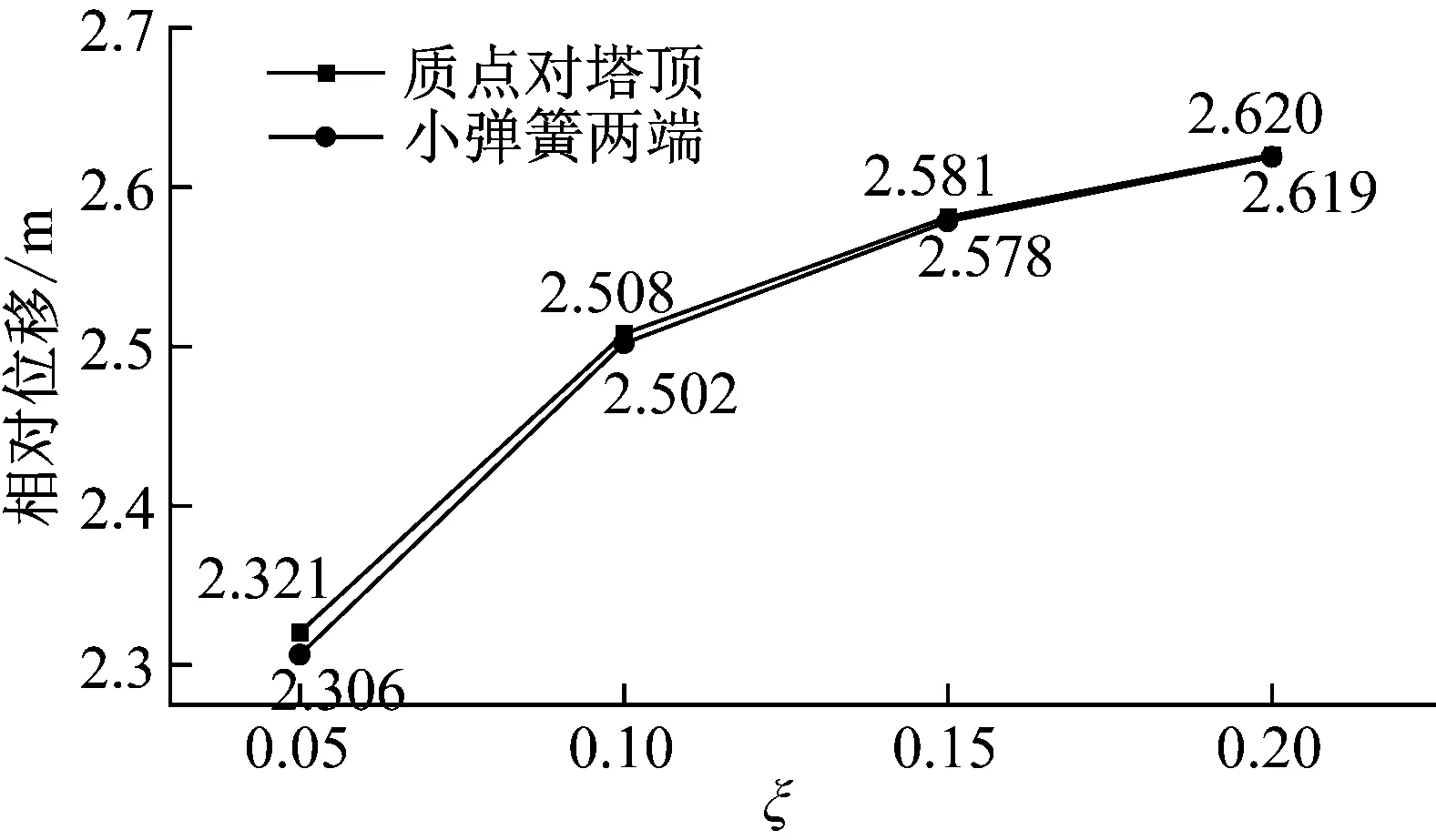
图21 不同ξ值TPIMS在随机荷载下的相对位移对比图
从图20和图21可知,增大阻尼比ξ能提升TPIMS的减振率,但同时也会显著增加质点的相对位移。这是因为过大的阻尼比会限制阻尼器自身的运动,进而导致耗能能力的减弱。
从上可知,在实际工程中,需要注意控制TPIMS中质点的行程与惯容器、小弹簧两端的相对位移。
5 结 语
本研究针对高耸三维结构难以计算涡振响应的问题,提出了基于有限元的迭代方法,并采用有限元方法建立了TMD与TPIMS模型,对比了基本接近简谐形式的涡激荷载与随机脉动风荷载下两者的减振效率,得到的结论为:
(1)对于三维高耸烟囱结构,使用基于有限元的迭代法能够较为准确地预测三维烟囱结构在不同风速下的涡振响应,且计算过程避免了复杂微分方程的求解,大大降低数学计算难度。
(2)惯容阻尼器TPIMS相比调谐质量阻尼器TMD,能够做到在相同质量比下大幅提高减振率,或在相似减振率下大幅降低减振系统自重。
(3)在实际工程中,TPIMS存在惯容器两端相对位移可能较大,增大小弹簧刚度ks或是在一定范围内降低阻尼器阻尼比ξ有助于控制质点相对位移,但同时也会导致TPIMS减振率下降,这一点需要在具体工程设计中加以关注。
