能量等效大跨屋盖结构三分量多目标等效静力风荷载

李玉学，冯励睿，李海云，田玉基

(1.石家庄铁道大学 土木工程学院，石家庄 050043；2.河北省风工程与风能利用工程技术创新中心，石家庄 050043；3.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043；4.北京交通大学 结构风工程与城市风环境北京市重点实验室，北京 100044)

等效静力风荷载是联系风工程师和结构工程师的桥梁和纽带，其实质是将结构的脉动风致动力效应转化为静力问题进行分析，此概念由Davenport[1]提出以来便得到了广泛关注，经过不少学者的完善和发展，目前针对高层、高耸结构的等效静力风荷载分析方法已经逐步成熟，包括阵风荷载因子法[2-3]、惯性力法[4-5]以及荷载响应相关法[6-7]等，上述分析方法在不同国家建筑结构荷载规范中也多有体现[8-12]。

与高层、高耸结构相比，大跨屋盖结构节点数目众多、自振频率分布密集，其风振响应具有多模态参与的特点，脉动风荷载作用下不同位置的节点不能在同一时刻达到极值，使得该类结构需要针对多个响应控制目标分别求解其等效静力风荷载，所得多组等效静力风荷载给结构工程师使用带来诸多不便，为解决这一问题，需要研究能够兼顾多个响应控制目标的等效静力风荷载分析法，即求解多目标等效静力风荷载，对此国内外许多学者进行了探索。段旻等[13]提出了包络多目标等效静力风荷载的概念，即针对多个关键目标响应求解得到的多组等效静力风荷载，采用对其取包络线的处理方法得到包络多目标等效静力风荷载。Tamura等[14]则针对多个关键目标响应求解得到的多组等效静力风荷载，对其取平均值作为多目标等效静力风荷载。Zhou等[15]根据各等效静力风荷载在其他响应上的等效精度对其分组，基于分组结果，采用数值方法求解对应的一致等效静力风荷载，以实现用较少的静风荷载分布等效多个目标响应。Patruno等[16]和Katsumura等[17]分别将多组脉动风荷载本征表皮模态和本征正交模态作为等效静力风荷载的基本分布模式，并采用最小二乘法计算其最优组合系数，以得到多目标等效静力风荷载。Yang等[18]针对大跨屋盖结构脉动风振背景响应和共振响应，分别以多组脉动风荷载本征正交模态和主要参振模态的惯性力作为基本分量，构造并数值求解多目标等效静力风荷载方程。李玉学等[19]根据结构风振响应特性，分别推导了构造多目标等效静力风荷载方程的背景、共振及其二者耦合项分量，由最小二乘法求解得到了具有统计意义的多目标等效静力风荷载。可见，目前大跨屋盖结构多目标等效静力风荷载求解，多数基于多个关键目标响应所得多组等效静力风荷载或其它荷载分布模式，采用数值处理方法得到统计意义上能够最大程度兼顾多个响应目标的等效静力风荷载，其优点是思路简单、处理方便，缺点是此数值处理方法缺乏明确的物理意义，仅为了实现多个响应目标数值等效，且有时所得多目标等效静力风荷载会出现局部突变，无法与结构自重等进行荷载组合。

大跨屋盖结构风致振动可以看作脉动风荷载对结构的做功过程，结构能量的改变综合反映了其风致动力效应，同时与能够较好反映风荷载作用机理的脉动风振背景响应、共振响应及其二者耦合项(简称三分量)相对应，基于能量等效，从保证结构安全角度，分别研究大跨屋盖结构三分量多目标等效静力风荷载，不仅能够较好地兼顾多个目标响应，而且相比于现有数值处理方法，物理意义更明确。因此，本文将分别推导基于能量等效的大跨屋盖结构三分量多目标等效静力风荷载，在此基础上，定义各分量能量贡献系数，据此系数对结构进行三分量响应层次划分，根据划分结果，实现大跨屋盖结构多目标等效静力风荷载的分层组合计算。

1 风振响应背景、共振及其耦合项三分量

大跨屋盖结构在脉动风荷载作用下的运动方程为

(1)

选取风振响应贡献较大的m阶主要参振模态[20]，由模态叠加原理可得结构位移响应

Xd(t)=K-1LPd(t)+[ΦQ(t)-ΦH0ΦTLPd(t)]

(2)

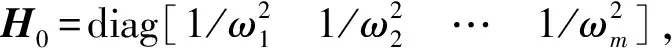
根据脉动风振背景、共振响应的概念[21]，式(2)右边第一项为背景响应Xd,b(t)，表示脉动风荷载的准静力效应，中括号项为共振响应Xd,r(t)。

根据随机振动理论，由式(2)可得结构某一节点k上总位移响应方差

(3)

式(3)为结构脉动风振响应三分量完全组合结果，即背景、共振及其二者耦合项组合。

2 能量等效三分量多目标等效静力风荷载

与式(3)表示的脉动风振响应三分量完全组合相对应，结构第k节点上多目标等效静力风荷载也应由背景分量Feq,b,k、共振分量Feq,r,k及其耦合项分量Feq,br,k组成。本章将基于能量等效对此三分量多目标等效静力风荷载分别推导。

2.1 背景分量多目标等效静力风荷载

根据式(2)，脉动风荷载作用下结构瞬时能量背景分量可以表示为

(4)

式中,∑diag[·]为矩阵的对角线元素求和。

定义由风洞试验测压点转换到结构第k、第l节点上的脉动风荷载分别为pk(t)和pl(t)，即荷载向量LPd(t)中元素，则式(4)可以进一步表示为

(5)

式中:fkl为结构柔度矩阵K-1T相应位置的元素；n为结构节点总数。

根据方差定义，由式(5)可得结构瞬时能量背景分量方差

(6)

式中:pkl(t)为结构第k、第l节点上脉动风荷载pk(t)、pl(t)相应元素的乘积；prs(t)为结构第r、第s节点上脉动风荷载pr(t)、ps(t)相应元素的乘积。

根据协方差定义，由式(5)可得结构瞬时能量背景分量Wb(t)和脉动风荷载乘积pkl(t)的协方差

(7)

由式(6)和式(7)，可以将结构瞬时能量背景分量Wb(t)的均方根表示为

(8)

式中,ρPkl(t),Wb(t)为脉动风荷载乘积pkl(t)与结构瞬时能量背景分量Wb(t)的相关系数。

由式(8)可得结构能量背景分量极值

(9)

式中,gWb为由极值超越理论计算得到的结构能量背景分量峰值因子。

根据式(5)结构能量背景分量定义，由式(9)可以得到保证结构能量背景分量等效的结构第k节点上多目标等效静力风荷载为

(10)

2.2 共振分量多目标等效静力风荷载

(11)

式中:qr,j(t)为结构第j阶广义模态坐标的共振分量；Xd,r,j(t)和Pd,r,j(t)分别为结构第j阶模态位移响应共振分量及其对应的恢复力列向量。

定义Pd,r,j(t)在结构第k、第l节点上对应元素分别为pr,j,k(t)和pr,j,l(t)，则式(11)进一步表示为

(12)

为表示方便，令

(13)

按照2.1节背景分量多目标等效静力风荷载推导过程，参照式(5)～式(10)可以得到保证结构第j阶模态能量共振分量等效的结构第k节点上多目标等效静力风荷载为

(14)

式中：gWr,j为由极值超越理论计算得到的结构第j阶模态能量共振分量峰值因子；ρPr,j,kk(t),Wr,j(t)为Pr,j,kk(t)和Wr,j(t)的相关系数，其中Pr,j,kk(t)为第j阶模态位移响应共振分量对应的恢复力列向量在结构第k节点上相应元素的自乘积；σPr,j,kk(t)为Pr,j,kk(t)的均方根。

考虑m阶主要参振模态，组合得到结构能量共振分量等效的结构第k节点上多目标等效静力风荷载

(15)

式中，λr,j为第j阶模态能量共振分量多目标等效静力风荷载的权重系数，表达式为

(16)

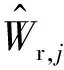
(17)

式中,Pr,j,kl(t)为第j阶模态位移响应共振分量对应的恢复力列向量在结构第k、第l节点上相应元素的乘积。

2.3 背景、共振耦合项分量多目标等效静力风荷载

(18)

式中:qbr,j(t)为结构第j阶广义模态坐标的背景、共振耦合项分量；Xd,br,j(t)和Pd,br,j(t)分别为结构第j阶模态位移响应背景、共振耦合项分量及其对应的恢复力列向量。

定义Pd,br,j(t)在结构第k、第l节点上对应元素分别为pbr,j,k(t)和pbr,j,l(t)，则式(18)进一步表示为

(19)

为表示方便，令

(20)

同样，按照2.1节背景分量多目标等效静力风荷载推导过程，参照式(5)～式(10)及式(15)可以得到保证结构能量背景、共振耦合项分量等效的结构第k节点上多目标等效静力风荷载

(21)

式中,Feq,br,j,k和λbr,j分别为保证结构第j阶模态能量背景、共振耦合项分量等效的结构第k节点上多目标等效静力风荷载及其相应的权重系数，表达式分别为式(22)和式(23)。

(22)

式中:gWbr,j为由极值超越理论计算得到的结构第j阶模态能量背景、共振耦合项分量峰值因子；ρPbr,j,kk(t),Wbr,j(t)为Pbr,j,kk(t)和Wbr,j(t)的相关系数，其中Pbr,j,kk(t)为第j阶模态位移响应背景、共振耦合项分量对应的恢复力列向量在结构第k节点上相应元素的自乘积；σPbr,j,kk(t)为Pbr,j,kk(t)的均方根。

(23)

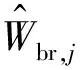
(24)

式中,Pbr,j,kl(t)为第j阶模态位移响应背景、共振耦合项分量对应的恢复力列向量在结构第k、第l节点上相应元素的乘积。

2.4 三分量多目标等效静力风荷载

至此，综合考虑平均风荷载以及由式(10)、式(15)和式(21)所得能量等效三分量多目标等效静力风荷载，结构总等效静力风荷载可以表示为

βbrFeq,br,k)

(25)

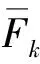
(26)

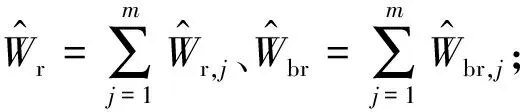
工程实际中，若能根据背景、共振及其二者耦合项三分量对总响应的贡献程度，对式(25)所示多目标等效静力风荷载进行分层次求解，便可有效兼顾多目标等效静力风荷载的计算效率和计算精度。

3 三分量多目标等效静力风荷载分层计算

3.1 三分量响应层次划分指标

本节将根据背景、共振及其二者耦合项三分量对总响应的贡献程度，对结构三分量响应进行层次划分，由于脉动风荷载作用下结构能量能够综合反映结构所有节点的响应，因此选取并定义三分量能量贡献系数ηi作为结构三分量响应层次划分指标，统一表示为

(27)

式中,符号含义同式(26)。

由式(27)计算所得各分量能量贡献系数ηi值，并根据工程经验综合考虑工程精度要求确定相应的误差限值εi，将结构三分量响应划分为I～VI层次，如表1所示。

3.2 等效静力风荷载分层计算

根据表1结构三分量响应层次划分结果，由第2章所得三分量多目标等效静力风荷载，可以给出大跨屋盖结构多目标等效静力风荷载分层计算方法。

对于I层次弱耦合柔性结构，需要计及共振分量，可以忽略背景分量及其背景、共振耦合项分量，据此由式(25)可得此层次结构总等效静力风荷载

(28)

式中,组合系数βr需要根据取舍以后的三分量由式(26)计算得到。

对于II～VI层次结构，同样根据表1描述结果，将式(25)中相应的等效静力风荷载分量进行取舍，便可得到其总等效静力风荷载组合结果，具体如表2所示。

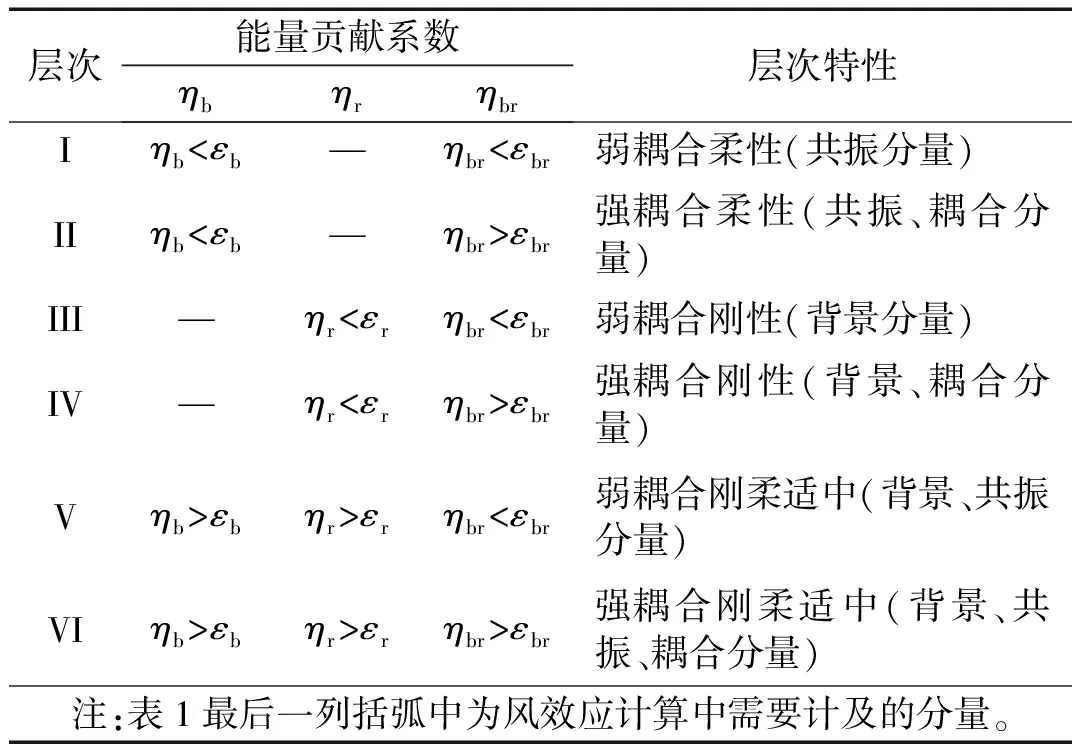
表1 大跨屋盖结构三分量响应层次划分表

表2 三分量多目标等效静力风荷载分层计算表

4 本文所提方法的主要分析步骤

本文所提基于能量等效三分量组合大跨屋盖结构多目标等效静力风荷载分层分析方法，主要步骤包括：

步骤1进行大跨屋盖结构风荷载同步测压风洞试验，得到屋盖表面平均和脉动风荷载数据，同时借助有限元软件进行结构动力特性分析，得到各阶模态分布、自振频率等动力特性信息。

步骤2利用步骤1所得屋盖表面风荷载数据和结构动力特性信息，进行结构脉动风振响应计算，根据风振响应计算结果由式(27)分别得到各分量能量贡献系数ηi，同时根据工程经验综合考虑工程精度要求确定相应的误差限值εi，由此误差限及表1综合判定结构三分量响应层次。

步骤3根据步骤2确定的结构三分量响应层次，合理取舍其三分量，相应的分别选择式(10)、式(15)和式(21)计算需要计及的等效静力风荷载分量，在此基础上，按照表2组合得到结构总等效静力风荷载。

5 算例分析

根据本文所提能量等效大跨屋盖结构三分量多目标等效静力风荷载分层分析方法，以北京奥林匹克公园网球中心赛场屋盖结构为例，对其三分量响应层次进行划分，根据划分结果组合计算结构总等效静力风荷载及其该总等效静力风荷载作用下结构静力响应，并与基于随机振动理论的频域分析所得目标响应进行对比，以验证方法的有效性。

5.1 工程概况

北京奥林匹克公园网球中心赛场屋盖结构新颖，整体形如“莲花”造型，由12个“Z”字形单元围绕圆心对称布置而成，如图1所示。“Z”字形单元悬挑长度21.6 m，最高点标高23.0 m，水平倾角约3°，以方便屋顶排水。此屋盖属于重要且体型复杂的结构，对风荷载敏感，需要借助同步测压风洞试验获取结构表面风荷载数据以进行风效应分析。

图1 北京奥林匹克公园网球中心赛场屋盖

5.2 风荷载测压试验及自振特性分析

屋盖结构模型风荷载同步测压试验在北京大学力学与工程科学系低速风洞中进行，采用有机玻璃和ABS板按照1∶120制作了屋盖结构缩尺模型，并保证满足风洞测压试验所需的模型强度和刚度要求。考虑到结构对称性，仅在模型第3和第4单元的上、下表面对应布置风荷载测点，测点总数156个，每个测点采样数据3 900个，采样频率400 Hz，风场按照B类粗糙度设置，测试时在0°～360°内间隔7.5°转动模型一次并采集数据，其中屋盖模型、风向角定义、单元编号及测点布置如图2所示。

图2 屋盖模型、风向角定义、单元编号及测压点布置

利用有限元软件建立屋盖结构计算模型，进行自振特性分析，计算并提取了前100阶模态的模态分布向量和自振频率，图3所示为前100阶自振频率分布，可见该屋盖属于典型的频率分布密集型结构，风致动力效应分析需要考虑多阶参振模态。

图3 前100阶模态自振频率分布

5.3 结构三分量响应层次划分及等效静力风荷载组合

由5.2节结构自振特性分析可知，该屋盖风致动力效应分析需要计及多阶参振模态，因此，按照李玉学等所述方法，从前100阶模态中共选定了17阶主要参振模态，分别为第1、第2、第4、第3、第6阶等。

利用5.2节所述屋盖模型同步测压风洞试验所得0°风向角下结构表面风荷载数据，按照本文所提方法，由所选定的17阶主要参振模态，计算了屋盖结构背景、共振及其二者耦合项三分量能量贡献系数ηb、ηr和ηbr，分别为0.433、0.521和0.046，误差限εb、εr和εbr统一取0.05，根据表1将该屋盖三分量响应划分为第V层次，即结构三分量等效静力风荷载组合时可以舍去背景、共振二者耦合项分量。

按照上述该屋盖三分量响应第V层次划分结果，分别由式(10)和式(15)计算了其背景、共振分量多目标等效静力风荷载，并依据表2组合得到结构总等效静力风荷载，将其表示为无量纲的风压系数形式，如图4所示。

由图4可知，本文方法所得总等效静力风荷载风压系数在屋盖结构绝大部分区域数值为负，表现为风吸力。在来流方向上第1、第7号单元，其负风压系数绝对值较两侧单元要大，比如7号单元的悬挑端迎风前缘负风压系数绝对值达到1.5，且对同一单元来说，悬挑端负风压系数绝对值较其它区域要大。

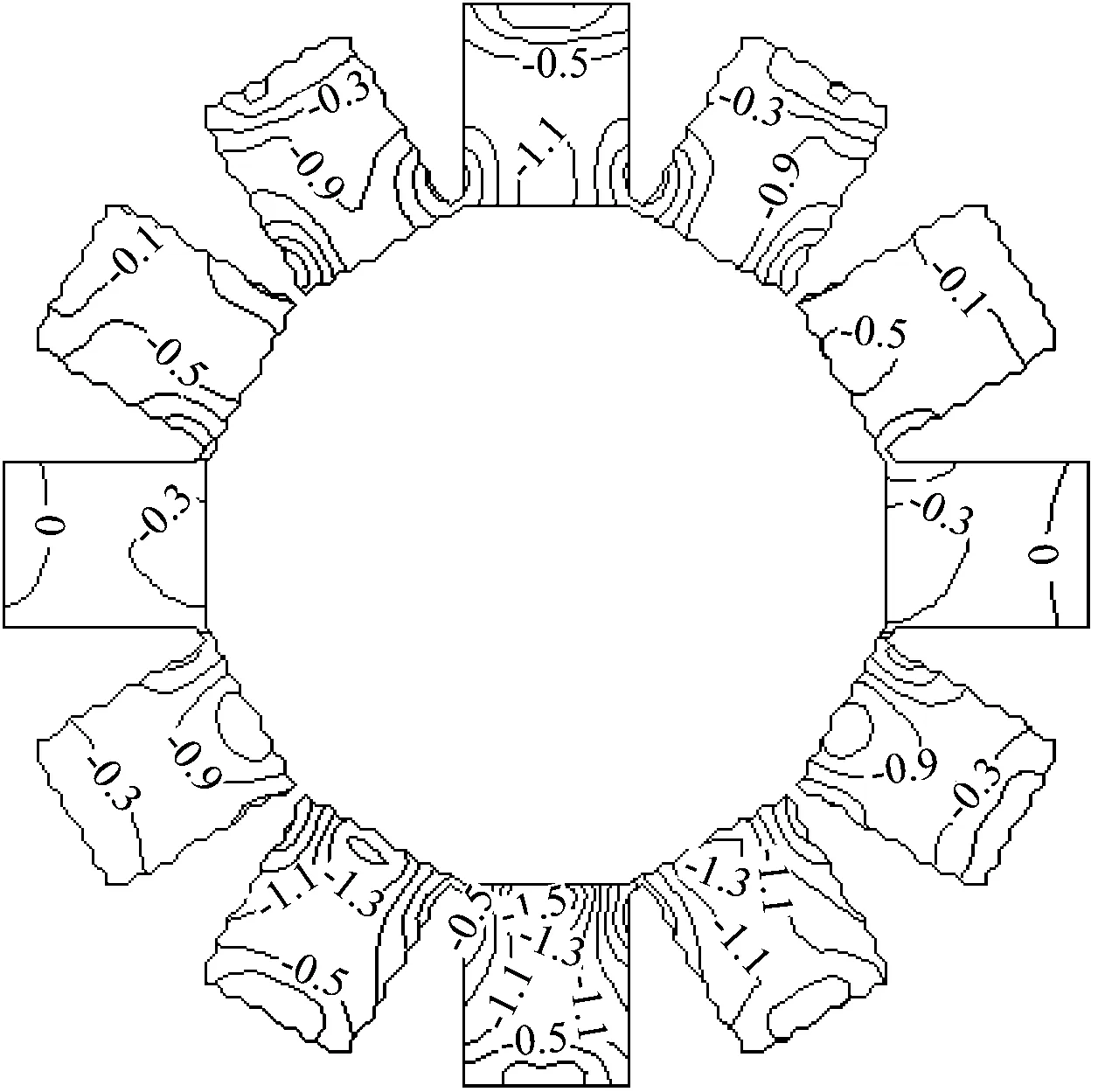
图4 本文方法所得总等效静力风荷载风压系数

5.4 结构静力响应计算结果分析

根据屋盖结构总等效静力风荷载风压系数求解结果(见图4)，计算了该总等效静力风荷载作用下的结构静力响应，并与基于随机振动理论的频域计算结果(目标响应)进行比较，其中典型节点位置及编号如图5所示。选取屋盖内环各个单元悬挑端(此处负风压系数绝对值较大，为风敏感位置)共48个典型节点对比结果如图6所示。

图5 典型节点位置及编号

图6 总等效静力风荷载作用下静力响应与目标响应对比

由图6可知，根据本文方法所得总等效静力风荷载作用下屋盖结构静力响应，与基于随机振动理论的频域计算所得目标响应总体吻合较好，误差稍大的几个节点(如15号、38号)其响应数值相对较小，对结构整体抗风设计不起控制作用，据此可以认为本文所得总等效静力风荷载能够满足实际工程需要。

6 结 论

本文针对大跨屋盖结构等效静力风荷载求解中的多响应目标问题，同时兼顾计算效率和计算精度，提出基于能量等效的三分量多目标等效静力风荷载分层分析方法，主要结论有：

(1)基于能量等效推导的大跨屋盖结构三分量等效静力风荷载，不仅能够较好地反映风荷载作用机理，与脉动风振背景响应、共振响应及其二者耦合项完全对应，而且能够综合考虑结构全部节点的响应，有效实现了兼顾多个响应目标。

(2)根据三分量响应对总响应能量的贡献程度，定义三分量能量贡献系数，据此实现了大跨屋盖结构三分量响应层次划分，根据划分结果，合理对相应三分量等效静力风荷载进行取舍，从而有效兼顾了总等效静力风荷载的计算效率和计算精度。

(3)以北京奥林匹克公园网球中心赛场屋盖结构为算例，采用本文所提方法，对其三分量响应层次划分，并根据划分结果进行结构总等效静力风荷载组合计算，通过比较所得总等效静力风荷载作用下结构静力响应与频域分析所得目标响应，说明所提方法能够满足工程应用要求。