超声清洗装置空化噪声谱分析法空化噪声级测量

吴博悦 陈 毅 李建成

(杭州应用声学研究所 杭州 310023)

0 引言

超声清洗机诞生于20 世纪50年代初的日本，历经数十年，现已发展应用到各个领域，成为其中重要的组成部分[1]。超声清洗的优点很多，如速度快、质量高，易于实现自动化等。它可以降低污物造成的伤害，减少污物与工作人员的接触；尤其是对于精密工件上的凹槽、狭缝、微孔及暗洞等传统的洗刷方法难以有效清洗的部位，超声清洗则有非常理想的效果[2]。

超声清洗过程中，其关键在于空化效应，但不能忽视空化腐蚀。因此，对超声清洗槽内空化强度进行准确、定量的测量就显得非常重要。对于空化强度的测量，研究人员多年来已利用空化的各种特点与性质，应用了如铝箔侵蚀法、碘滴定法、空化噪声谱分析法、声致发光法以及图像处理法等多种方法进行实验测量与研究[3−6]。空化噪声是由于在发生空化时，空化泡的线性与非线性脉动，空化泡的形成与破灭，以及空化泡之间的相互作用等因素而产生的，始终伴随着空化过程。测量空化噪声，可以得到其中关于空化过程中大量的信息，具有独特的优势。

其中，对于空化噪声，各国研究人员开展了一系列的研究。1956年，Holak[7]在ORL 消声箱和物理实验室水槽中，用Massa 115A 和一个Allen Spencer 探针水听器进行了空化噪声测量。他分析了90 kHz～2 MHz频率范围内的空化噪声；观察到除了宽带噪声外的驱动频率的谐波和次谐波成分；给出了与实验结果相吻合的空化气泡增长和衰减的表达式；计算得驱动频率及其谐波处出现的能量比宽带频谱中的能量更多。2000年，Frohly 等[8]研究了超声空化中空化噪声和空化强度的关系，在不同的超声功率下分别用空化噪声谐波及高次谐波的功率谱和连续谱的功率谱来表示空化强度。2005年，Sobotta 等[9]对超声清洗设备的空化噪声进行了测量，分析了空化噪声谱，研究了驱动超声频率f0处的声压在不同换能器表面声强时的变化情况。2014年，Hertz-Eichenrode等[10]测量了空化噪声信号频谱的“颜色”，确定了各谐波频段的噪声级与声强对数之间的线性度；并且通过空化噪声的测量，测量了瞬态空化阈值。2017年，Köchel 等[11]研究了对空化噪声谱的数字信号处理方法。2019年，文献[12]制定了用空化噪声级LCN和提取空化噪声谱分量获得空化噪声各个部分的分量来表示超声清洗槽中的空化强度。

本文利用空化噪声谱分析法，进行了超声清洗装置和超声清洗槽的空化噪声测量实验。实验较好地验证了利用空化噪声级来判断空化阈值和衡量空化强度的可行性；同时，研究了超声清洗装置和超声清洗槽内空化的分布情况，两者具有较大的差异。

1 空化噪声谱分析法

超声清洗利用超声引发空化效应，以此来达到清洗的目的。在发生瞬态空化时，气泡坍塌溃灭，同时产生的射流和冲击波作用于物体需要清洁的表面[13]。然而，空化的机械效应并不容易测量。因此，可以借助气泡非线性脉动及溃灭产生的噪声，定义空化噪声级来评估空化强度。

将水听器固定于运动控制装置上，在运动装置的带动下，按曲折的路径缓慢通过清洗槽，期间连续测量清洗槽中的声信号。采集信号后，用窗函数对数据进行加权，并将加权数据分别做快速傅里叶变换(Fast Fourier transform, FFT)。接着，计算这些由FFT得到的空化噪声谱的幅值均值的平方，相当于求了功率谱。取与空化相对应的谐波声压均值的平方，即。该值与参考声压pref的平方的比值取对数，得到空化噪声级为[12]

如图1(a)所示在超声清洗设备中，低频谐波0.25× f0(f0为超声清洗换能器的谐振频率)的噪声级很低，与声强的对数不成正比，而且空化阈值的位置也无法明显看出。在这些频率下，声波的半波长也明显大于清洗槽的尺寸。在频带为(2.25±0.1)×f0和(4.25±0.1)×f0时，空化阈值以上的噪声级与声强的对数成正比。在高频段(8.25±0.1)×f0和(16.25±0.1)×f0中，噪声级并不完全遵循函数1 和函数4(函数1 与函数4 分别为拟合的n/4 倍谐波曲线在瞬态空化前后的变化趋势函数)。同时，在(2.25±0.1)×f0的频段内干扰较少，故需选择测量中心频率fc= 2.25×f0处的噪声声压作为计算瞬态空化噪声级的声压。通过对超声清洗换能器的实际测量(超声换能器基频f0为24 kHz)，得到n/4 倍谐波噪声级情况与文献[10]中相同(函数a与函数b同图1(a)中的函数1与函数4)。

图1 n/4 倍谐波噪声级变化曲线Fig.1 The n/4 times harmonic noise level variation curve

IEC/TS 63001 标准中，采用单水听器运动测量，计算得2.25 倍谐波的谐波噪声级，并由此可得瞬态空化阈值，以其大于瞬态空化阈值的部分作为瞬态空化强度的衡量标准[12]。

Lauterforn 等[14]用n/2 倍谐波的出现作为判断液体稳态空化起始的标准，文中测得n/2 倍谐波的变化如图2(a)所示。通过对超声换能器的实际测量(超声换能器基频f0为24 kHz)，得到n/2 倍谐波噪声级变化如图2(b)所示。由于1/2倍谐波噪声级变化曲线在发生稳态空化后有长期下降阶段，不利于对稳态空化的表示，而在其他测量的n/2 谐波噪声级中，2.5倍谐波噪声级幅值最高，因此可选用2.5倍谐波噪声级表示稳态空化强度。

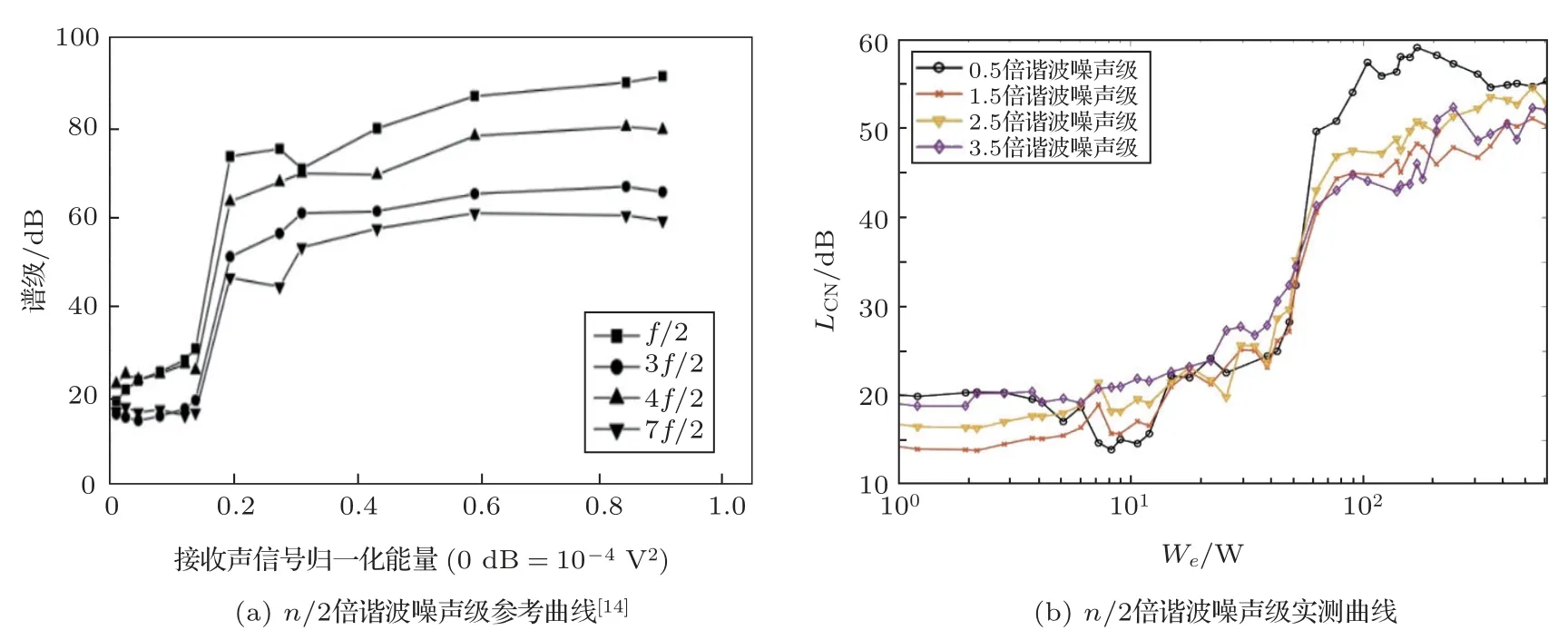
图2 n/2 倍谐波变化曲线Fig.2 The n/2 times harmonic noise level variation curve

由于超声清洗换能器实际测量时，于2.5 倍谐波出现时观察到长时间存在脉动气泡，对应稳态空化；于2.25 倍谐波在函数a 与函数b 的焦点处观察到气泡云，对应瞬态空化，因此，设2.5 倍谐波噪声级LCN-2.5为稳态空化噪声级，2.25倍谐波噪声级LCN-2.25为瞬态空化噪声级，以及表示稳态空化强度与瞬态空化强度。通常取pref=1 µPa。

2 测量系统的建立

2.1 测量对象

超声清洗换能器由杭州瑞利超声科技有限公司生产，内含有8 个超声振子，其尺寸(D×H)为59 mm×80 mm，以2×4 的排列结构封装于矩形盒内，如图3(a)、图3(b)所示，超声振子横向间隔85 mm，纵向间隔80 mm，均匀分布于封装之内。超声清洗换能器谐振频率为24 kHz，长35 cm，宽17.5 cm，高10 cm，最大输出功率2000 W。该超声清洗换能器可置于尺寸大于自身的水槽中，而后在水槽中加入足量的水进行超声清洗。

超声清洗槽底部焊有6 个超声振子，其尺寸(D×H)为45 mm×45 mm，如图3(c)、图3(d)所示，中心超声振子A 位于清洗槽中心位置，其余超声振子位置于图3(d)中标出。超声清洗槽谐振频率为41 kHz，长40 cm，宽30 cm，高25 cm。由于在水槽底部直接焊接超声振子，因此可在清洗槽中直接加水进行超声清洗。

图3 超声清洗换能器与超声清洗槽Fig.3 Ultrasonic cleaning transducer and ultrasonic cleaning bath

2.2 测量系统的设计

根据上述原理，设计了空化噪声级的测量实验。由于超声清洗换能器需置于大于自身尺寸的水槽中进行清洗，因此选择了某实验水槽作为超声清洗水槽，其长113 cm、宽68 cm、深77 cm，上方有运动控制装置，可以按需求，控制电机带动水听器在水槽中运动。实验设置水深40 cm。在本文中，为说叙述方便，称8 个振子的水槽为超声清洗装置，6 个振子的水槽为超声清洗槽。实验系统示意图如图4所示。

图4 超声清洗装置实验系统示意图Fig.4 Schematic diagram of ultrasonic cleaning device test system

超声清洗槽长40 cm、宽30 cm、深25 cm，将其置于运动控制装置运动范围之内，仍由控制电机带动水听器在水槽中运动。实验设置水深20 cm。其测量系统如图5所示。

图5 超声清洗槽实验系统示意图Fig.5 Schematic diagram of ultrasonic cleaning bath test system

测量系统中，发射端由信号源、功率放大器与超声换能器、超声清洗槽组成。其中功率放大器为HD-PA0830-6000 型，连续波输出最大功率为2000 W，脉冲输出最大功率为6000 W。信号源为KEYSIGHT 33600A型。

接收端由水听器、采集卡与示波器组成。水听器为RHS-5 水听器，灵敏度约为−218 dB(参考灵敏度为1 V/µPa)。采集卡为National Instruments的PXI-6368。示波器为Keysight DSOX3014A 型，最大采样率为5 GSa/s。

2.3 运动机构

多维运动定位机构包括两套独立的x、y、z、θ复合运动机构及其配套控制器。每套运动定位机构由纵向(y坐标)、横向(x坐标)、升降(z坐标)三维直线和回转(θ坐标)运动机构组成。两套运动机构的x、z和θ机构均能手动和电动控制。y运动机构一套为全手动控制，一套为手动和电动控制。计算机通过串行接口，实现对多维运动定位机构各个维度的扫描运动和定位控制。为方便说明测试平面、运动轨迹的确切位置，首先对超声清洗装置构建三维直角坐标系，如图6所示。

图6 超声清洗实验装置坐标Fig.6 Coordinate diagram of ultrasonic cleaning test device

坐标系每个单元对应实际长度为1 mm。根据运动装置的原始设定坐标系的x、y和z轴，即：水槽的宽方向为x轴，总长68 cm，范围为−340～340；水槽的长方向为y轴，总长113 cm，范围为−565～565；竖直方向为z轴，换能器上方部分长30 cm，范围为0～300，加上竖直方向其他部分，总长40 cm，范围则为−100～300。

由运动装置带动水听器，于距换能器12.5 cm处的xOy面，选择y= 0，x=−50～50；y=−30，x=−50～50；y=−60，x=−50～50；x=−50，y=−60～0；x= 0，y=−60～0 和x= 50，y=−60～0 共6 条线段组成的田字作为测量水听器的运动轨迹，如图7 所示。水听器的运动速度为5 mm/s。

图7 水听器运动轨迹示意图Fig.7 Schematic diagram of motion track of hydrophone

对超声清洗槽构建三维直角坐标系，与超声清洗装置相似，坐标系每个单元对应实际长度为1 mm，以超声清洗槽底面中心位置为原点，超声清洗槽长方向为x轴，总长40 cm，范围为−200～200；超声清洗槽宽方向为y轴，总长30 cm，范围为−150～150；竖直方向为z轴，水深20 cm，范围为0～200。

3 测量实验

3.1 超声清洗装置测量实验

3.1.1 单点测量

由于运动测量相对耗时，故而先选用单点测量对水槽内的空化阈值，以及观察随着输入功率的增加，换能器工作特性的变化。

根据换能器测得的声场分布所知，选择换能器表面上方12.5 cm处xOy面的中心位置作为测量点。功率放大器的阻抗分为6 挡，通过调节信号源输入电压来调节输入换能器的功率。

测量时，固定水听器于选定位置，将功率放大器与换能器阻抗匹配测验；由示波器监视功率放大器输出电压、电流及电压电流之间的相角，按5 mV或10 mV的步长从小到大增加换能器输出电压。数据处理流程图和测量结果如图8与图9所示。

图8 数据处理流程图Fig.8 Data processing flow chart

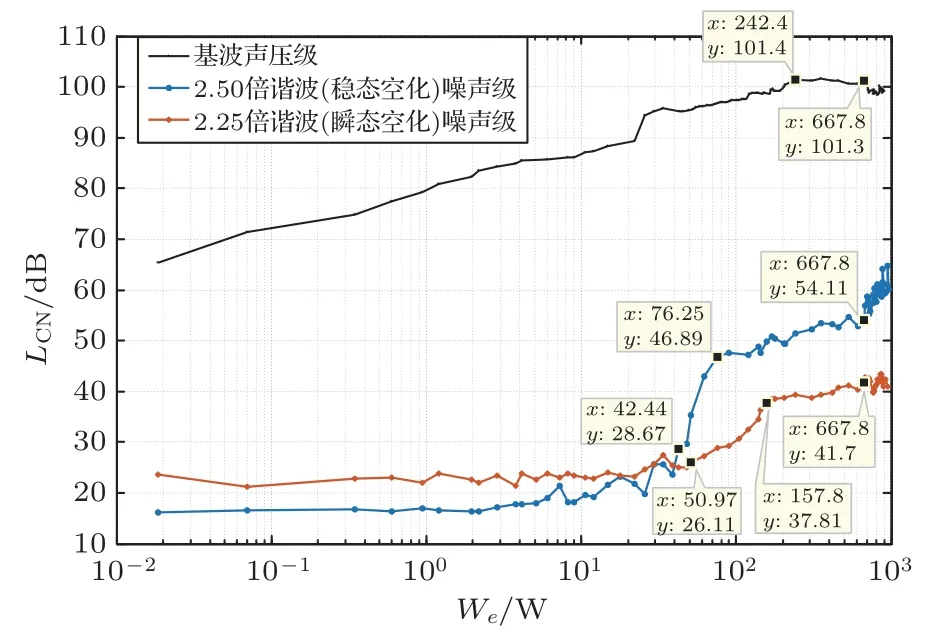
图9 单点测量超声清洗装置基频及谐波噪声级曲线Fig.9 Single point measurement of fundamental frequency and harmonic noise level curve of ultrasonic cleaning device

图9中，黑色曲线为基频声压级，在242.4 W以前具有较好的线性度，之后不再增加，换能器开始进入非线性工作状态。蓝色曲线为2.5 倍谐波噪声级，红色曲线为2.25 倍谐波噪声级。2.5 倍谐波从42.44 W左右开始大幅增长，根据前文所述理论，此时稳态空化出现；至76.25 W左右之后趋于平稳，呈缓慢增长状态，稳态空化接近饱和。2.25 倍谐波在50.97 W 出现开始大幅增长，转折点在157.8 W 左右出现，其增长速率明显下降，根据前文所述理论，此时瞬态空化出现。瞬态空化阈值对应的瞬态空化噪声级约为37.81 dB。在换能器输入电功率超过660 W 后，由于强瞬态空化与换能器严重非线性工作，测量值出现严重波动。

3.1.2 运动测量

由单点测量结果可知，应当特别关注40～70 W、120～200 W和350 W至最高输出功率的输入电功率段。由于设备原因，本次实验超声换能器输入功率最高只能达到550 W。测得结果如图10所示。

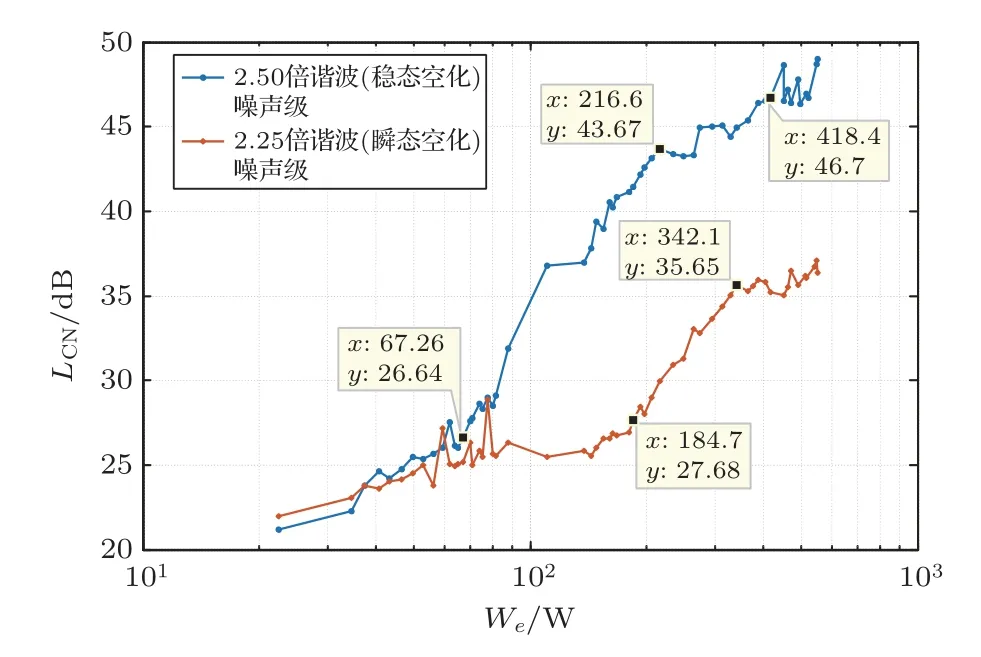
图10 超声清洗装置运动测量谐波噪声级曲线Fig.10 Harmonic noise level curve of motion measurement of ultrasonic cleaning device

图10 中，蓝色曲线为2.5 倍谐波噪声级，红色曲线为2.25 倍谐波噪声级。2.5 倍谐波从67.26 W左右开始大幅增长，稳态空化出现；至216.6 W 左右之后趋于平稳，呈缓慢增长状态。2.25 倍谐波在184.7 W 出现开始大幅增长，增长至342.1 W 出现转折点，其增长速率明显下降，瞬态空化由此开始。与单点测量比较，2.5倍谐波出现对应的输入电功率相差约20 W，而2.25倍谐波转折点(瞬态空化阈值)对应的输入电功率则相差更多，近200 W。

为进一步了解偏差的来源，取运动测量的运动路径中x方向和y方向的一段做空化分布分析。以水听器1 s运动的小段位移为微元，求不同输入电功率下各微元的谐波噪声级，结果如图11所示。

图11横坐标为线段上微元的位置；纵坐标为换能器输入电功率，自上而下功率依次增大；颜色由冷至暖，代表谐波噪声级的由小到大。由图11可知，在超声清洗装置的分析线段上，2.5倍谐波先于中间位置出现，表示稳态空化先于中间位置发生，又于某个时刻布满整条线段；2.25 倍谐波表示的瞬态空化同样先发生于换能器中间位置，但随着输入电功率不断增加，其空化位置相对集中于中间位置。

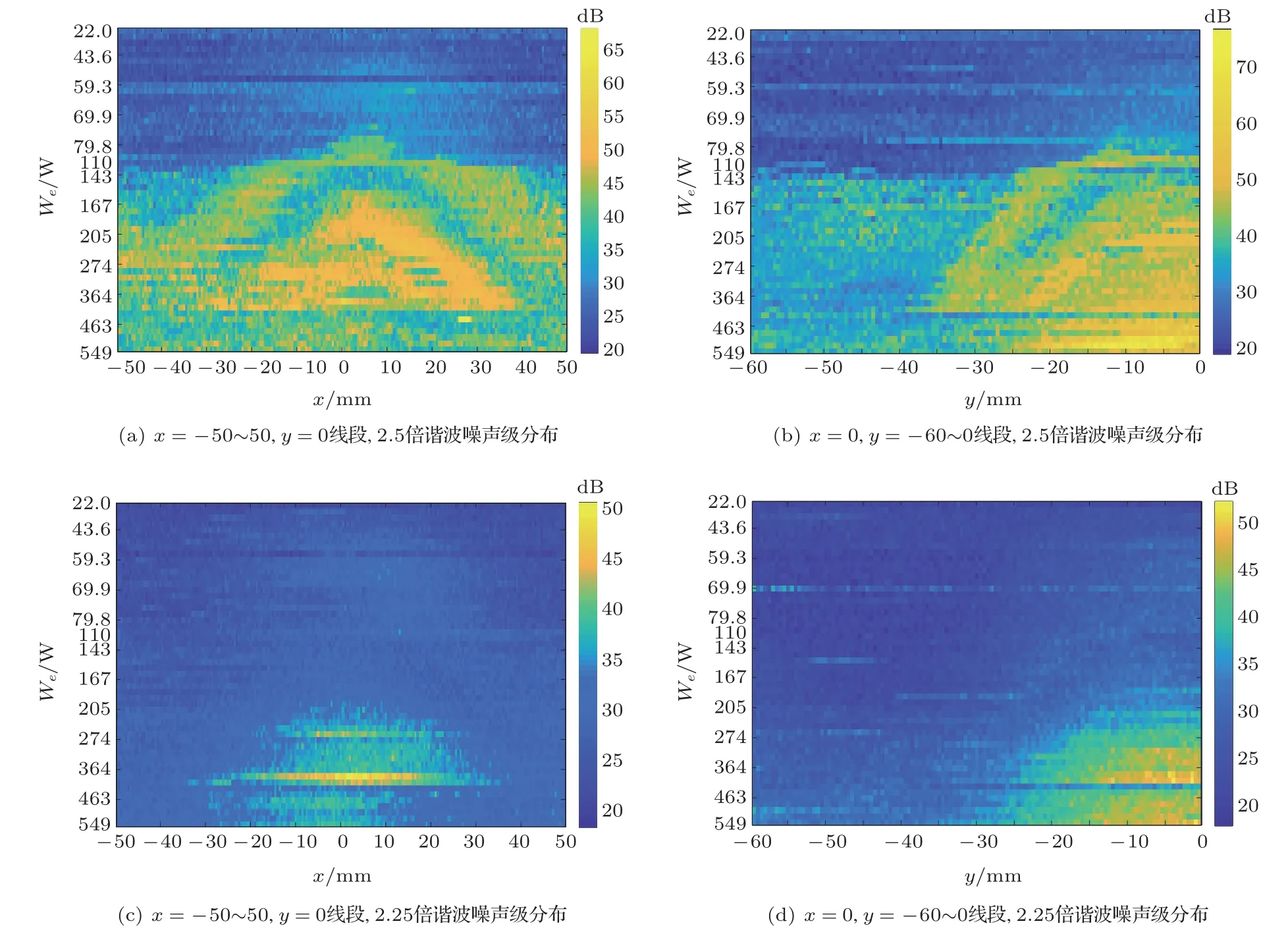
图11 超声清洗装置12.5 cm 处x=−50 ～50，y =0 线段与x=0，y =−60 ～0 线段上谐波噪声级分布图Fig.11 Distribution diagram of harmonic noise level on section x = −50 ～50, y = 0 and section x = 0,y =−60 ～0 at 12.5 cm of ultrasonic cleaning device

稳态空化由中间位置开始，随输入电功率的增加很快广泛分布于液体介质中，分布相对较为平均。此时空间平均之后的2.5 倍谐波噪声级与单点测量结果相近，并且空间平均更有利于反映超声清洗装置内稳态空化的整体情况。而瞬态空化发生的位置相对集中于某一小区域，微元测得的大值淹没于空间平均之中，因此两者测量结果相差较大。

3.2 超声清洗槽测量实验

对于超声清洗槽，根据测得的清洗槽中心垂直声场分布，选取清洗槽底面中心位置，z=20处作为运动轨迹平面。运动轨迹为x=−120～120，y=0与x=0，y=−70～70两条呈十字交叉的线段。测量结果如图12所示。

图12中，蓝色曲线为2.5倍谐波噪声级，红色曲线为2.25 倍谐波噪声级。2.5 倍谐波从0.1819 W 左右开始大幅增长，此时稳态空化出现；至1.266 W左右之后趋于平稳，呈缓慢增长状态，稳态空化接近饱和。2.25 倍谐波在0.4408 W 出现开始大幅增长，转折点在5.219 W 左右出现，其增长速率明显下降，此时瞬态空化出现。瞬态空化阈值对应的瞬态空化噪声级约为31.21 dB。

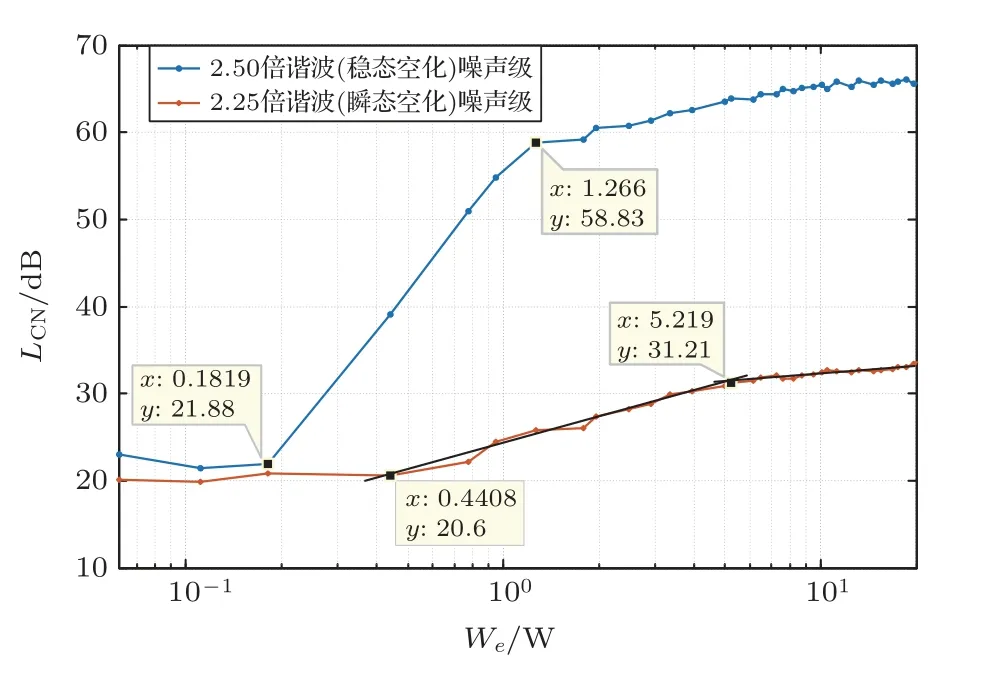
图12 超声清洗槽谐波噪声级曲线Fig.12 Harmonic noise level curve of ultrasonic cleaning bath

取运动测量的运动路径中x方向和y方向的一段做空化分布分析。以水听器1 s 运动的小段位移为微元，求不同输入电功率下各微元的谐波噪声级，结果如图13所示。

图13 超声清洗槽x=−120 ～120，y =0 线段与x=0，y =−70 ～70 线段上谐波噪声级分布图Fig.13 Distribution diagram of harmonic noise level on x=−120 ～120, y =0 section and x=0, y =−70 ～70 section of ultrasonic cleaning device bath

图13横坐标为线段上微元的位置；纵坐标为换能器输入电功率，自上而下功率依次增大；颜色由冷至暖，代表谐波噪声级的由小到大。由图13可知，在超声清洗槽的分析线段上，当达到稳态空化和瞬态空化阈值后，2.5倍谐波表示的稳态空化与2.25倍谐波表示的瞬态空化均匀的分布于分析线段上，稳态空化相比瞬态空化更为密集。此时，空间平均的空化噪声级可以较好地表示超声清洗槽中的空化强度。

4 讨论与结论

在超声清洗装置的声场环境下，由于稳态空化分布广泛，运动测量的空间平均值可以说明清洗槽内整体的稳态空化强度；但如果要追溯稳态空化的起始，则需从空化分布图中寻找率先出现2.5 倍谐波噪声级的位置，此时，水听器的运动轨迹选择至关重要。由于瞬态空化分布集中，运动测量时会使瞬态空化起始时少量的瞬态空化信号湮没在空间平均之中。因此，无法使用随机的空间平均说明清洗槽内整体的瞬态空化强度，应在瞬态空化集中区域进行测量。同样，在瞬态空化测量时水听器测量位置的选择至关重要。本文是根据超声清洗装置内抽取的几个平面的声场分布来选择测量位置与运动轨迹。对水听器测量位置与运动轨迹的其他选择依据与方法需在进一步研究中进行。

在超声清洗槽的声场环境中，测量曲线各个变化环节分界点明显，稳态空化与瞬态空化都分布均匀，空间平均能较好地说明清洗槽内整体的稳态空化与瞬态空化状况。在该环境下，计算空间平均得到的空化噪声级能较好地表示空化强度。

本文测量空化分布实验中，如果水听器在某位置的测量结果中出现2.5 倍谐波或2.25 倍谐波噪声级大于瞬态空化阈值，则认为水听器测量点附近发生稳态空化或瞬态空化。从结果来看，该方法有效。但对于稳态空化时气泡脉动与瞬态空化时气泡破灭产生的辐射噪声，以及与水听器测量的关系仍需进一步研究。

通过本次实验研究可得以下结论：

(1)在不同的环境下，空化噪声级都能较好的表示液体介质中的空化强度(2.5 倍谐波噪声级可以表示稳态空化强度，2.25 倍谐波噪声级可以表示瞬态空化强度)，不受换能器基频f0影响。

(2)在超声清洗装置(超声清洗换能器置于大于其自身尺寸的水槽中)环境下，由于稳态空化分布广泛，运动测量的空间平均值可以说明清洗槽内整体的稳态空化强度；瞬态空化分布集中，无法使用随机的空间平均说明清洗槽内整体的瞬态空化强度，应在瞬态空化集中区域进行测量。

(3)在超声清洗装置(超声清洗换能器置于大于其自身尺寸的水槽中)环境下，水听器空化噪声谱分析法测量空化强度时，水听器选取的测量位置、运动路径对测量的影响效果较大。对水听器测量位置与运动路径的选择也需要在后续的工作中进一步研究。

(4)在超声清洗槽(超声振子焊接于清洗槽下)的声场环境中，稳态空化与瞬态空化都分布均匀，计算空间平均得到的空化噪声级能较好地表示空化强度。

(5)空化噪声级的大小、趋势与空化的发展过程相对应。精确地得到空化阈值，与了解水槽中空化的发展过程对超声清洗及其他与空化相关的应用具有重要意义，对此将在后续的研究中进一步进行。

致谢感谢林书玉教授、余宏沛教授对本文实验结果的指导与肯定；感谢杨柳青、刘玉财对实验数据处理给予的帮助；感谢国防科技工业水声一级计量站提供实验场地，感谢黄勇军、平自红、王世全以及杭州瑞利超声科技有限公司提供的实验设备支持。