子带t分布的快速独立向量分析在语声盲源分离中的应用∗

康 坊 杨飞然 杨 军

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

盲源分离(Blind source separation, BSS)旨在将感兴趣的信号从混合信号当中分离出来，可广泛应用于声频信号处理领域，其中一个重要应用是语声分离。相较于有监督的分离算法[1]，BSS 可以在没有任何传输信道信息和声源先验信息的情况下从卷积混合的观测信号中无监督地分离出原始声源。频域独立成分分析(Independent component analysis, ICA)[2−5]作为解决卷积BSS 问题的一类广泛且经典的方法，需要在各个频点上独立建模并独立分离源信号的各个频率成分，因此无法确保不同频点间声源顺序的一致性，即存在顺序模糊性问题。独立向量分析(Independent vector analysis, IVA)[6]以及其改进的辅助函数IVA(Auxiliaryfunction IVA, AuxIVA)[7]通过在全频带建立球对称联合概率密度函数，使得同一声源的各频率成分具有统一的频间依赖性，有效地减轻了顺序模糊性问题，提高了分离性能。然而，统一的频间依赖假设导致声源模型缺少灵活性，可能导致子带间出现顺序错排的问题。为了更好地表征声频信号中相近频点或谐波频点的依赖性要强于较远频点的特点，基于子带依赖性假设的声源模型[8−10]被提出以用于增强相关频点、弱化不相关频点的依赖性。此外，为了提高AuxIVA 算法的收敛速度和稳定性，改进的快速迭代IVA(本文简称Fast AuxIVA)算法[11]通过秩1 更新的方式来估计分离信号，避免估计分离滤波器带来的矩阵求逆，降低计算复杂度和数值不稳定性，但并未提升分离性能。

为了进一步提升IVA 算法在语声分离任务中的分离性能和稳定性，本文提出一种基于子带声源模型的快速IVA 算法，并采用更适合语声信号重尾特性的t分布[12]作为声源概率密度函数。该算法首先根据信号特性将全频带划分为多个子带，其中包含一个重叠子带，在各个子带内假设声源服从联合t 分布，由于子带间的重叠设置使得各个子带间依然具有频间依赖性。此外，该算法将声源模型联合秩1 更新方法，推导出新的空间模型参数优化准则，在基于子带t 分布的声源模型下实现混合语声信号的快速分离。实验结果表明，本文提出的算法能够在少量的迭代次数下取得比目前已有的IVA 算法更好的语声分离性能。

1 快速AuxIVA算法

1.1 混合和分离模型

假设正定BSS 中N个声源信号由N个传声器信号接收，声源信号、估计的声源信号以及观测信号的频域复数表示分别为

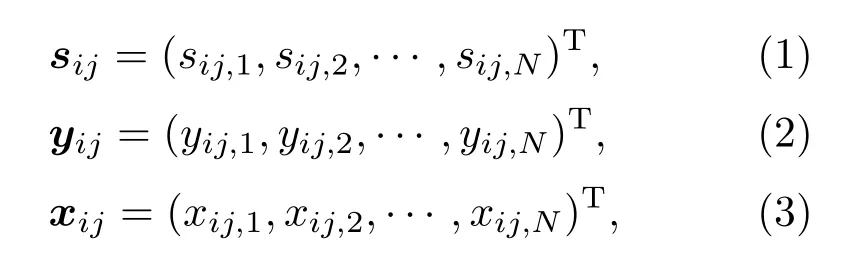
其中，i= 1,2,··· ,I为频率索引(I为频点数)，j= 1,2,··· ,J为时间索引(J是帧数)，(·)T表示矩阵转置。经过短时傅里叶变换(Short-time Fourier transform, STFT)后，时域卷积混合模型可以变换到频域瞬时混合模型，

其中，Ai是N ×N的混合矩阵。当Ai可逆时，混合矩阵Wi=(wi1,wi2,··· ,wiN)H可以被定义成Ai的逆矩阵，因此分离信号yij可以通过以下公式恢复得到，

其中，wi,n=(wi,n1,wi,n2,··· ,wi,nN)T是第n个声源的分离向量，(·)H表示矩阵共轭转置。

1.2 声源估计的快速迭代算法

在IVA 中，根据式(5)以及声源间的独立性假设，观测信号xij在所有时间帧上的负对数似然函数可表示为

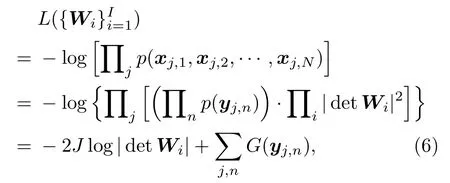
其中，G(yj,n)=−logp(yj,n)为对比函数。在超高斯假设下，声源的概率密度函数p(yj,n)可表示为

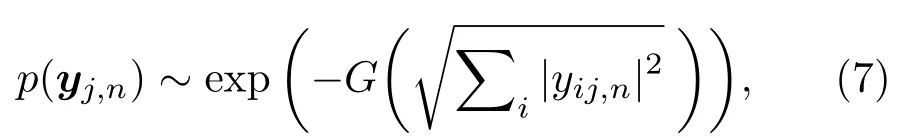
其中，G(·)需要满足φ(r)=G′(r)/(2r)在r >0 时单调递减，(·)′表示微分。分离矩阵Wi可以通过最小化式(6)中的目标函数得到，进而估计出分离信号yij。

为了更快更稳定地优化分离矩阵，AuxIVA 算法构建辅助目标函数Q()代替直接求解

其中，Vi,n是辅助变量。 通过不断最小化Q()和更新辅助变量Vi,n来逼近原函数的最优解，因此得到以下迭代准则：

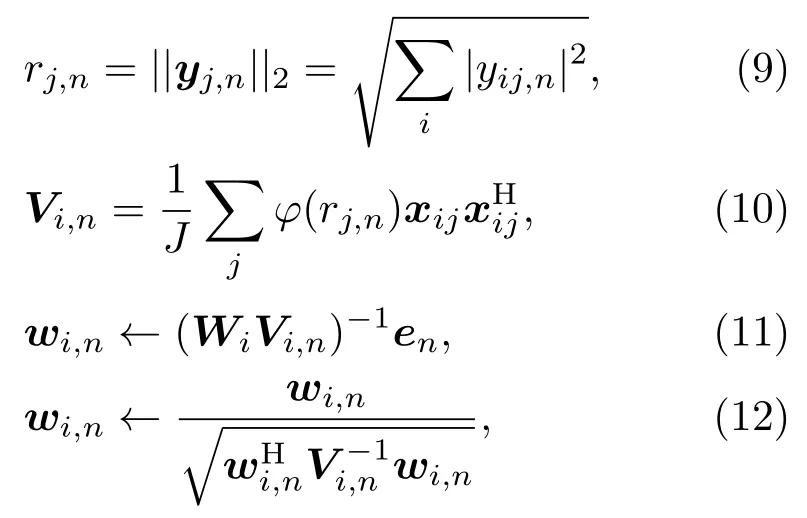
其中，en是第n个元素为1 的单位向量。上述迭代准则适用于多种声源模型，但需要在每次迭代时计算N个辅助变量矩阵和N个矩阵的逆。此外，当矩阵病态时，求逆操作在迭代过程中可能导致数值不稳定。

为了避免矩阵求逆，降低计算复杂度，文献[11]提出一种秩1更新的方式来优化Wi，

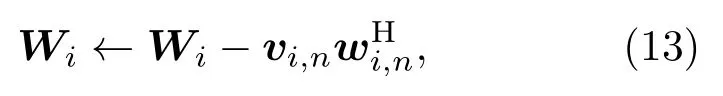
其中，vi,n=(vi,n1,vi,n1,··· ,vi,nN)T是待估计的优化向量。将式(13)代入辅助函数Q得到

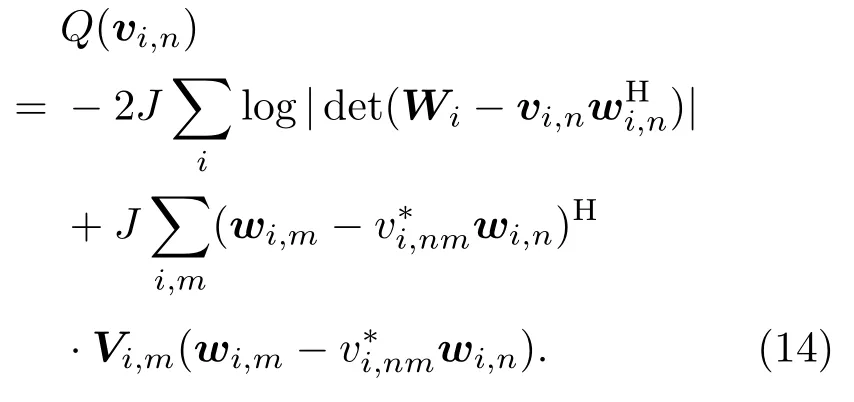
最小化上述目标函数可得到vi,n的优化准则，

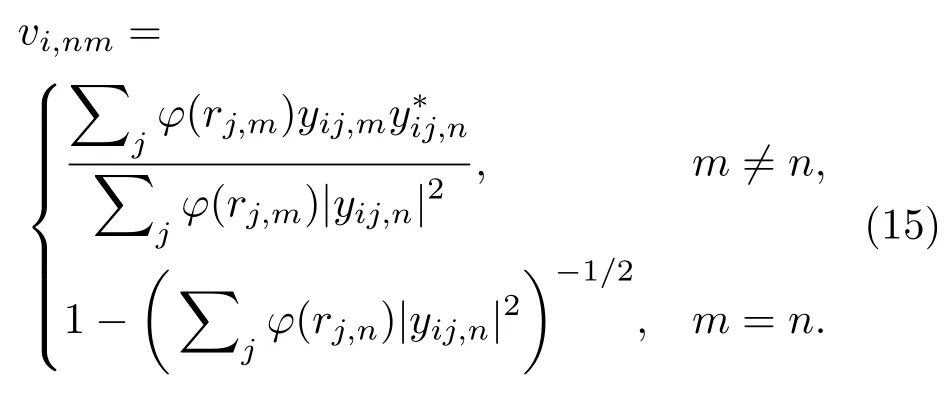
根据式(13)，得到yij新的计算公式：

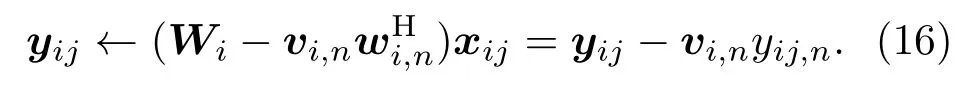
因此分离信号的估计不需要计算分离矩阵Wi，与迭代过程式(9)～(12)不同，Fast AuxIVA 的迭代过程式(15)～(16)不需要矩阵求逆操作。

2 基于子带t分布的快速AuxIVA算法

2.1 算法原理

为了增强声源模型相邻频点间的依赖性来避免分离过程中出现的顺序模糊性问题，本文将全频带划分为C个子带，并假设声源在各子带内独立服从如下分布：

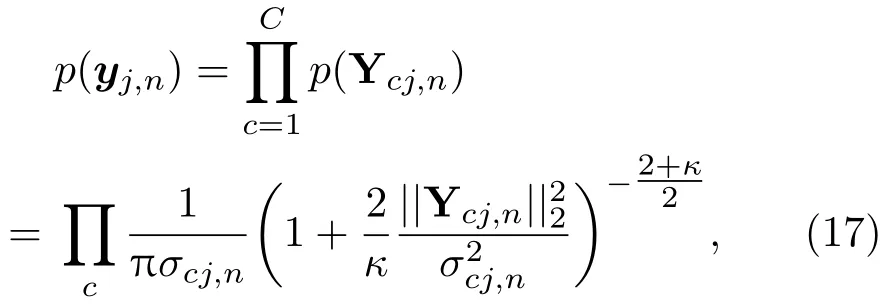
其中，Ycj,n={yij,n}i∈Ωc，Ωc表示第c个子带内的频点集合，κ是自由度参数，κ越大，分布越接近于高斯分布，σcj,n是第c个子带的时变尺度参数。由于语声信号的时变特性，在不同时间帧上引入不同的时变参数σcj,n更有利于表示声源的能量变化情况，且同一子带内的所有频点共用相同的σcj,n，建立了频率间的依赖性。前C −1 个子带采用无重叠划分方式，保证子带内的频点拥有一致的高阶依赖性。但无重叠的设置会让子带间缺少依赖性而导致带间的顺序不确定问题，因此在第C个子带中包含了所有频点，与其他子带均有重叠，增加子带间的依赖性，从而避免了子带间顺序校正的后处理操作。将式(17)中的声源模型代入目标函数式(6)可得

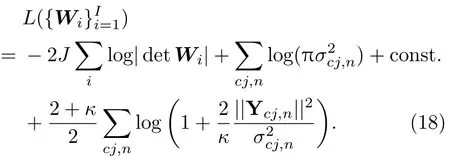
σcj,n的估计可通过对得到，其中NΩc表示集合Ωc的元素个数。σcj,n可以看作是对当前时刻的信号能量求期望，能够表示声源在时间维度上的活动情况。此外，同一子带内的各个频点共用相同的σcj,n，这说明子带内的各频点信号协同出现，具有较强的频间依赖性。

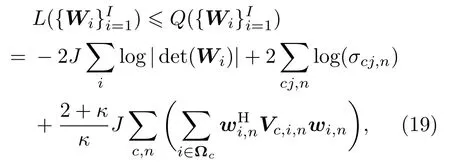
其中，

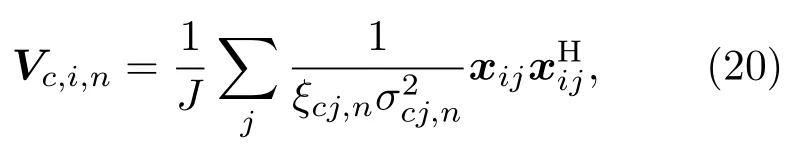
可以看作是第c个子带内，观测信号的加权协方差矩阵。当辅助变量时，式(19)中等号成立。为了快速估计分离信号，将本文采用的声源模型与秩1 更新的优化方法结合，推导出新的空间参数优化准则。首先将分离矩阵的更新方式(式(16))代入式(19)得到目标函数：

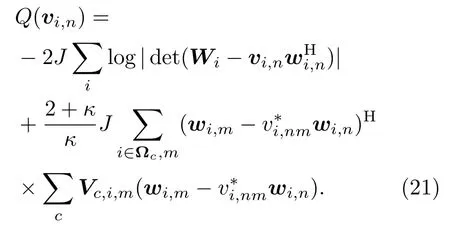
通过最小化Q(vi,n)得到关于vi,n的如下优化准则：

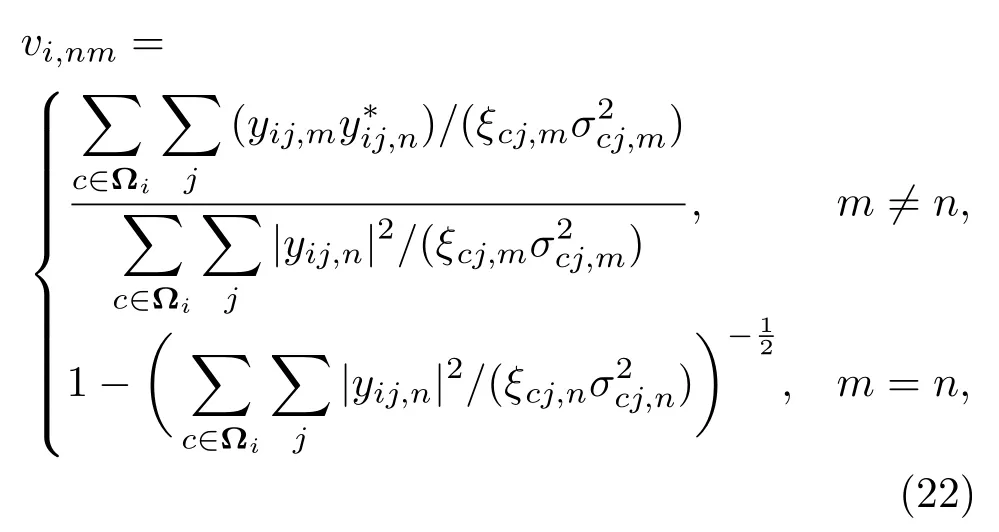
其中，Ωi表示包含第i个频点的子带集合。由于子带的重叠设置，在计算频点i上的辅助变量vi,nm时，需要考虑所包含该频点的所有子带内的信息。这说明在参数估计中引入了频带间的依赖性，从而避免子带间的声源顺序错排问题。

通过上述迭代准则，交替更新式(22)和式(16)，避免了分离矩阵的更新和存储以及矩阵求逆操作，并且可在少量的迭代后达到收敛。最后的分离信号yij通过(16)计算得到。

2.2 计算复杂度分析

计算复杂度是衡量算法性能的重要指标之一，本节将重点分析AuxIVA、Fast AuxIVA 和所提出的算法在更新过程中的复杂度。在AuxIVA 中，计算复杂度主要取决于协方差矩阵Vi,n的计算和分离矩阵Wi的计算。以复数乘法为单位，在各频点上Vi,n的复杂度为O(N3J)，Wi的复杂度为O(N4)。通常情况下，帧数J远大于声源个数，因此，在一次迭代中遍历所有频点，AuxIVA 所需的计算复杂度为

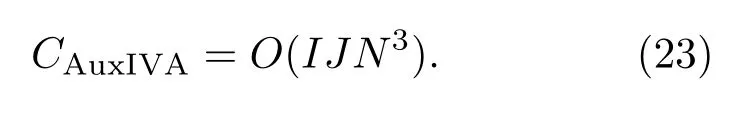
Fast AuxIVA的计算复杂度主要取决于式(15)中vi,nm的计算。在一次迭代中，遍历所有频点和声源所需的计算复杂度为

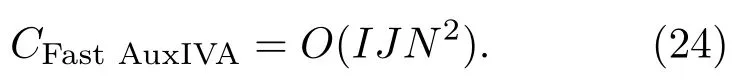
该计算量相当于AuxIVA算法计算一次协方差矩阵的计算量，因此需要计算协方差矩阵的分离算法，其计算复杂度均要大于Fast AuxIVA算法。

在提出的基于子带t 分布的Fast AuxIVA 中，由于重叠子带的引入，计算重叠频点的参数时需要对重叠子带个数Nc求和，而t 分布的声源模型相较于传统模型未增加额外的计算量，因此计算复杂度为

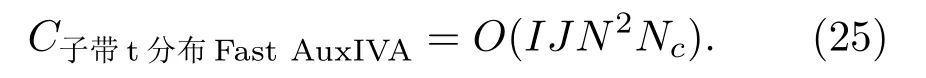
本文提出的模型中，仅采用一个全频点子带与来建立其他非重叠子带间的依赖性，因此Nc= 2 ≤N。由此可得，基于子带t 分布的Fast AuxIVA复杂度满足

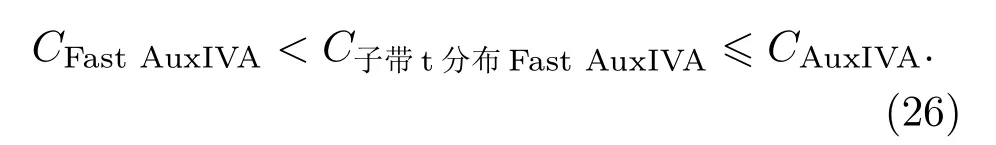
所提算法在更新参数时所需的计算复杂度介于传统AuxIVA算法和Fast AuxIVA算法之间。

3 仿真实验

3.1 实验环境设置

分离实验所需要的房间脉冲响应来自RWCP库[13]中实际测量的不同场景下的混响数据，分别为E2A(RT60= 300 ms)、JR2(RT60= 470 ms)、JR1(RT60= 600 ms)、OFC(RT60= 780 ms)和E2B(RT60= 1300 ms)。以两种不同声源位置布局的E2A 和JR2 为例，实验环境设置如图1 所示。对于纯净语声数据，从TIMIT 数据库[14]中随机选择120 位录制者、长度为8 s 的测试语料。在两声源混合(N= 2)中，测试语料分别与不同混响时间的脉冲响应卷积得到混合数据(包括男-男混合、男-女混合和女-女混合各20 组)。所有的数据采样率为16000 Hz。对于混响时间为300 ms 的混合信号，STFT窗长为256 ms；对混响时间大于300 ms的混合信号，STFT 窗长为512 ms，帧移均为1/4 窗长。在AuxIVA 算法中，Wi初始化为单位矩阵。在所有算法中总迭代次数设置为10N。选择BSS EVAL 3.0[15]中的信号干扰比(Signal to interference ratio, SIR)和信号失真比(Signal to distortion ratio,SDR)作为分离性能的评价指标。

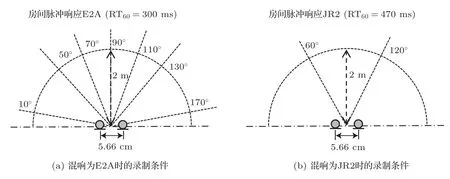
图1 实验环境设置Fig.1 Simulated room environment

3.2 不同子带划分方式对分离性能影响

子带划分方式会影响声源频点间的依赖程度。为了探讨不同的划分方式对分离性能的影响，本文测试了在4 种不同的划分方式下SIR 和SDR 的提升结果。如图2 所示，图2(a)～图2(d)分别为重叠子带均匀划分、重叠子带非均匀划分、无重叠子带均匀划分和无重叠子带非均匀划分，其中在无重叠划分中为了避免子带间的模糊性，额外引入一个全频点子带。

图2 不同子带划分方式Fig.2 Different frequency clique divisions

按照图2 中的划分方式，在E2A(声源位置50◦和130◦)和JR2 下进行分离实验，其中κ= 1。图3给出了各子带划分方式在30 组独立实验下的平均分离结果。从图3 中可以看出，在混响时间较短的E2A下，不同的子带划分方式对分离性能的影响较小。这是因为当混响时间较短时，STFT窗长更能覆盖房间脉冲响应长度，频域瞬时模型的假设更容易成立，分离任务简单。由于在简单的分离任务下发生顺序模糊性的概率较低，所以避免模糊性的子带模型作用相对不明显。当混响时间增加，如图3(b)所示，分离任务难度增大，此时对声源模型的准确性要求更高，不同的子带划分方式对分离结果影响较大。在4 种划分方式中，无重叠划分要略优于重叠子带划分，其中无重叠均匀划分取得了最优的分离结果。因为重叠子带划分方式会使得同一子带内重叠部分的频点与非重叠部分频点间声源模型参数不一致，而无重叠子带划分方式保留了子带内频点间统一的依赖性，更有利于避免顺序模糊性问题。根据此实验结果，在后续实验中均选用如图2(c)所示的无重叠均匀划分方式。

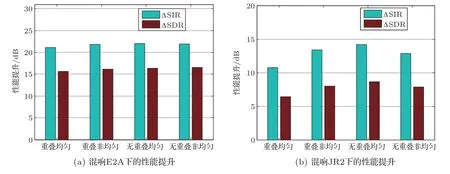
图3 不同子带划分方式下的分离性能Fig.3 Separation performance with different frequency clique divisions

3.3 自由度选择对分离性能影响

为了探讨提出的改进算法在不同t 分布自由度下的分离性能， 分别设置自由度为κ={1,2,5,10,50,100}。每种自由度设置下，实验结果是60 组混合数据分离后的平均值。其中E2A 下声源位置选择50◦和130◦。

从图4 中可以看出，无论是在混响时间300 ms还是470 ms 时，改进的算法在自由度κ= 1 时分离性能最优。随着自由度κ的增大，假设的声源概率密度函数逐渐接近高斯分布，分离性能逐渐下降，这也说明语声信号的分布更符合重尾分布，在合适的声源模型下能取得更好的分离结果。因此，在后续实验中，经验选取自由度κ=1。

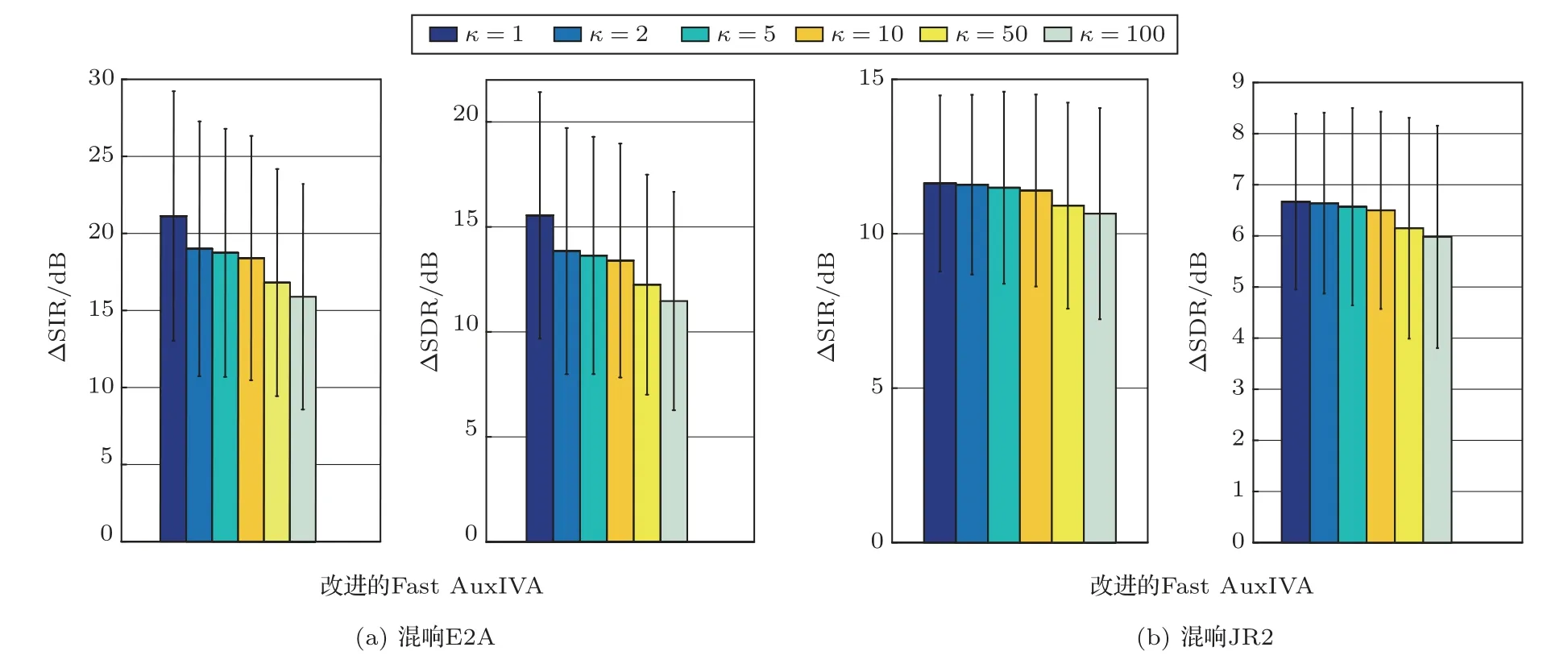
图4 不同自由度下所提算法的分离性能Fig.4 Separation performance with different κ

3.4 不同环境下分离性能对比

本文对比了传统AuxIVA[7]和Fast AuxIVA[11]算法，并将子带超高斯模型引入到AuxIVA 和Fast AuxIVA中，来进一步对比验证子带t分布模型的合理性和有效性。在每种实验条件下，对30 组混合数据分离后的平均结果进行了对比。首先验证了上述算法在不同声源位置下的分离性能。各声源组合为图1(a)E2A中的声源位置(10◦，90◦)、(10◦，170◦)、(50◦，70◦)、(50◦，130◦)和(130◦，170◦)。

图5 给出了不同声源位置下，各算法的SIR 和SDR 结果。可以看出引入子带模型后，各算法均有较明显的性能提升，说明子带模型更能表示声源内相邻频点比相距较远频点有更高频间依赖性的特征。在子带模型中，基于t分布的改进算法取得了整体最优的分离性能，也进一步说明t 分布比传统超高斯分布更符合语声信号的重尾特性。此外，对于相距较近的声源，所有算法的分离性能均有所下降，这是因为当声源位置较近时，不同声源与传声器之间的传递函数相似度更高，在估计各个声源的分离滤波器时难度也越大。

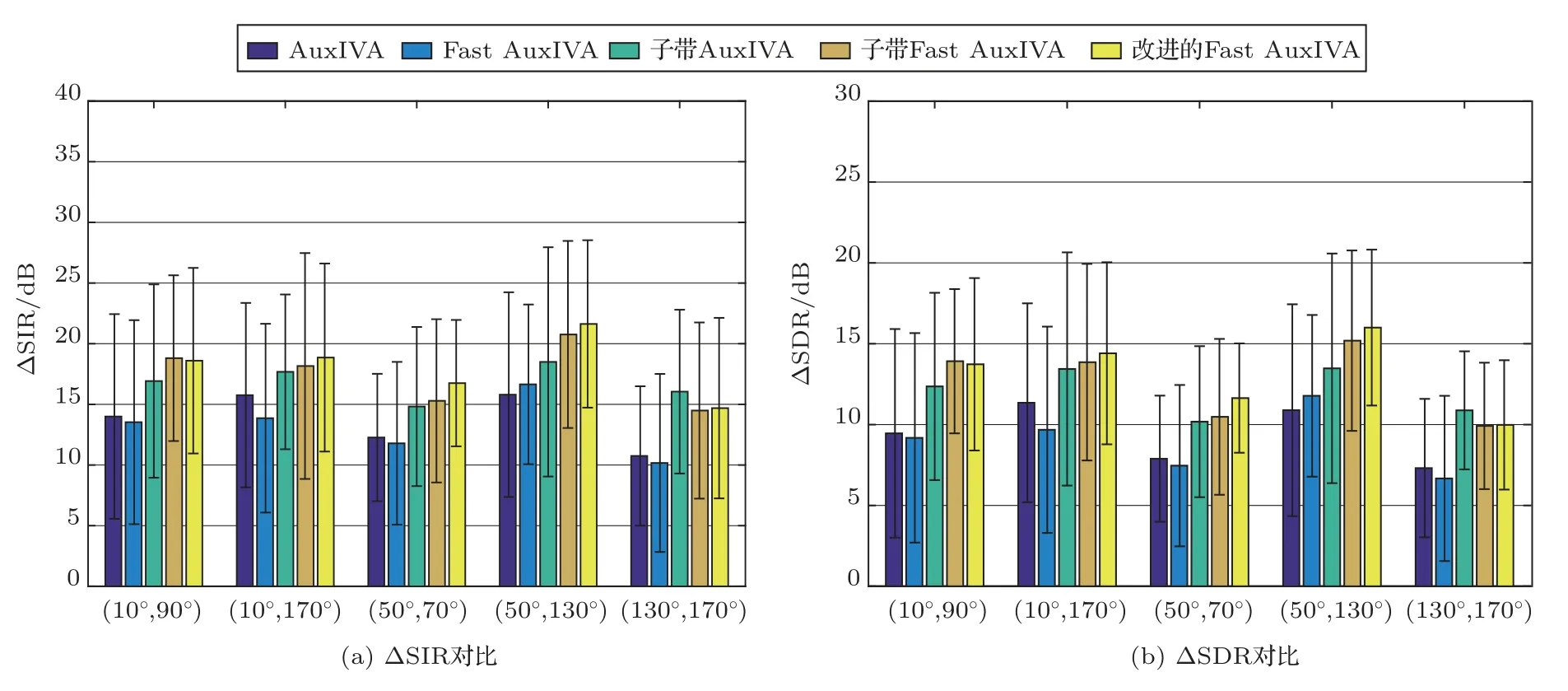
图5 不同声源位置下的分离性能对比Fig.5 Comparison of different algorithms for different source locations

为了进一步验证算法的分离性能，给出了不同混响时间下各算法的SIR 和SDR 提升结果。除JR2 声源位置布放为60◦和120◦，其他混响时间下声源位置均选择50◦和130◦。从图6中可以看出，混响时间对分离性能影响明显，但混响超过300 ms的条件下，分离性能变化较小。其中一个原因是超过300 ms 的数据均采用一样的STFT 窗长，信号在各频点上的时间序列长度相同，因此分离信号满足统计独立性假设的程度类似。此外，当混响严重时，子带划分的声源模型要比传统模型的性能提升更加明显，这是因为随着分离难度的增加，分离算法对声源模型的准确性要求更高，一个更精确的声源模型能够取得更好的分离结果。改进的基于子带t 分布的声源模型，在各混响条件下均取得了最优的分离性能，这也进一步说明了该模型更适合语声分离任务。

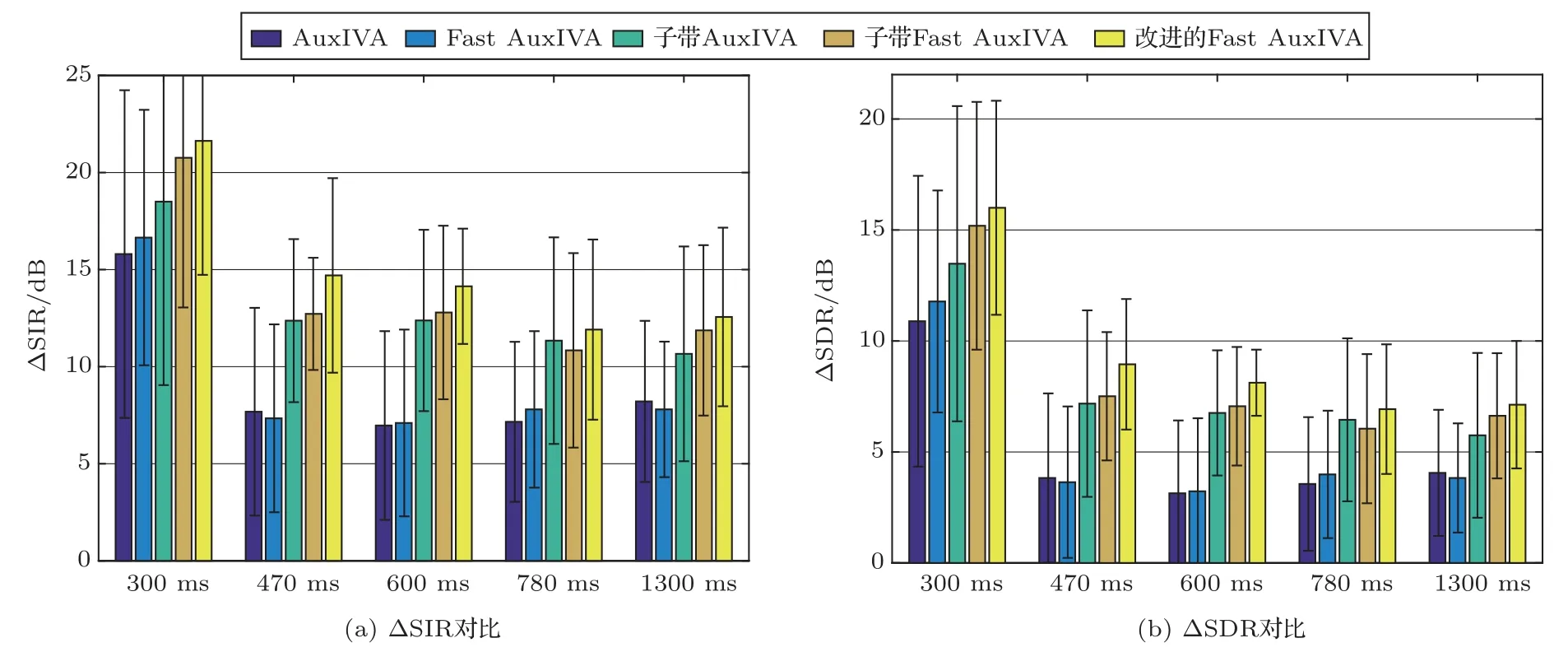
图6 不同混响时间下的分离性能对比Fig.6 Comparison of different algorithms for different reverberation time

3.5 不同算法的复杂度对比

除了分析不同算法的分离性能之外，本文也比较了上述5 种算法在本文参数设置下的计算复杂度。与所提算法相似，子带AuxIVA 和子带Fast AuxIVA 的计算复杂度相较于各自对应的非子带模型而言，其区别在于重叠子带个数的设置。因此，子带Fast AuxIVA 和所提出的算法具有相同的计算复杂度。各算法在更新参数时的复数乘法次数结果如图7所示。

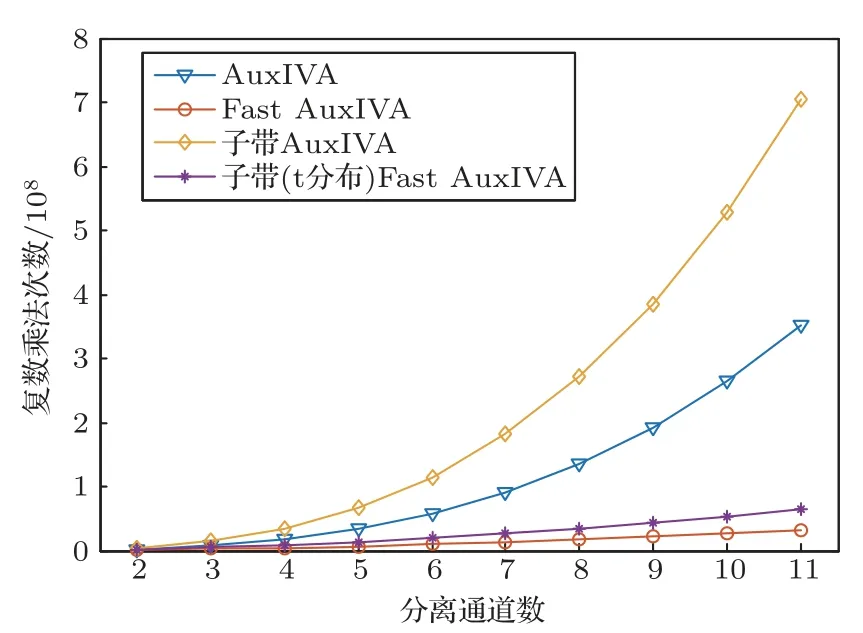
图7 计算复杂度对比Fig.7 Computational complexity comparison

从图7 可以看出，各算法的计算复杂度差异随着分离通道数(即分离声源个数)的增加而愈加明显。在所有算法中，Fast AuxIVA 并未进行子带划分，因此计算复杂度最低。子带(t 分布)Fast AuxIVA 复杂度略高于Fast AuxIVA，但却明显低于未采用快速迭代的AuxIVA 及其子带算法。结合分离结果可以看出，与Fast AuxIVA 相比，子带(t分布)Fast AuxIVA在轻微增加计算代价的情况下，实现了分离性能的明显提升；与传统AuxIVA 和子带AuxIVA相比，取得更好的分离结果的同时，显著地降低了计算复杂度。

4 结论

本文提出了一种基于子带t 分布的Fast Aux-IVA 算法，采用更适合语声统计特性的子带t 分布声源模型，并结合秩1更新的快速迭代方法，推导出了改进的优化更新准则。该迭代准则避免了优化过程中矩阵求逆操作，提高了分离算法的稳定性和计算有效性。为了保证子带内各频点间具有统一的高阶依赖性，算法首先采用无重叠的方式对频带进行划分。同时，为避免子带划分导致的带间顺序模糊性问题，本文利用一个全频子带建立子带间的依赖性。实验结果表明，相较于AuxIVA和Fast AuxIVA算法，提出的方法可以在语声分离任务中进一步提升分离性能。