导向相应功率定位中时延不确定项的影响∗

黄毅伟 佟建飞 张文琼 胡小青 鲍 明

(1 中国科学院声学研究所 噪声与振动重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

分布式无线声传感器网络(Distributed wireless acoustic sensor networks, DWASNs)在军事安防[1−2]、生态环境监测[3−4]等领域均有广泛的应用。声源定位是无线声传感器网络的关键技术之一，也是目标识别、监测与跟踪等应用的前提，通过从传声器接收到的声源信息中提取相关测量信息，如声能量强度(Received signal strength,RSS)[5−6]、波达时间差(Time difference of arrival,TDOA)[7−10]和声源波达方向角(Direction of arrival, DOA)[11−12]等，来实现声源位置的估计。

传统的声源定位方法中测量信息往往需要在前端中进行信号处理，在复杂环境中，声源定位的性能容易受到局部错误量测的干扰。可控波束形成器导向相应功率(Steered response power, SRP)，则是将传感器构成的波束形成器的空间SRP 作为定位函数，通过搜索空间功率谱图中最大值估计声源的方位或位置，是一种有效的声阵列测向[13−17]和声源定位方法[18−19]。该方法避免了间接量测所导致的声源信息损失，在混响和复杂声环境下具有更稳健的定位性能。

SRP 方法在应用中面临的最主要的问题是计算耗时太长。目前主要采用广义互相关(Generalized cross-correlation,GCC)形式的SRP函数[13]简化计算过程。为了进一步降低全局网格搜索的计算量，国内外学者展开了大量研究，基于随机区域重建[15]和遗传算法[20]等方法不再进行全局搜索但也因此无法保证信息完整性，文献[21]提出了基于TDOA 梯度设计非均匀网格以降低空间采样数量的方法。另一类方法通过改进SRP 函数来适应粗网格[22]或进行分层搜索[18]。MSRP[22]方法计算空间谱图时设计了一种改进的SRP 函数，用网格点对应的一段时间窗内GCC 的累加值替代格点对应的GCC 取值带入原SRP 函数实现了网格自适应性，这种方法兼顾了稳定性和搜索运算量。

传统的SRP 方法要求传声器节点的导向时延估计非常准确，在声源测向与室内定位中具有良好的稳定性能。对于户外定位应用场景，来自硬件系统(如节点同步、自定位误差)和环境因素的干扰(如温度、风速变化等)使得导向时延出现不确定性，实际传播时延和理论计算结果的误差导致空间功率难以聚焦于实际的声源位置，降低了SRP 声源定位方法的鲁棒性。

本文针对传声器网络SRP 声源定位中导向时延不确定性问题，在经典SRP 定位模型中引入导向时延的不确定项，对其组成因素进行了建模和量化分析，改进了MSRP 函数中累加求和的范围，并提出了基于最大值滤波的声源定位方法。该方法增设了最大值滤波器对GCC 进行处理，扩展导向时延不确定项在对应空间点处的TDOA范围，保证SRP功率函数在声源位置能够取得最大值。通过仿真与外场实验验证本算法在传声器网络声源定位应用中的稳定性和优越的定位性能。

1 问题描述

1.1 基于SRP和WASN的声源定位模型

设N-维欧氏空间下布设M个分布式传声器(M > N)，向量x ∈RN表示空间内坐标，xs表示声源坐标，zm表示传声器的空间坐标(m= 1,2,··· ,M)。忽略多径传播与非线性传播现象，位于zm处的传声器接收的信号在频域上可表示为

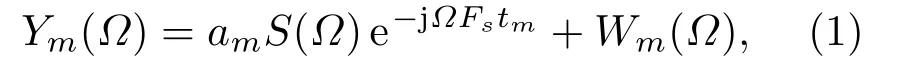
其中，Ω ∈[−π,π]表示归一化角频率，am和tm分别表示传播过程中的幅度衰减因子与时延因子，S(Ω)是和Wm(Ω)分别表示声源信号和加性噪声的傅里叶变换，Fs是系统采样频率。

SRP函数可表示为

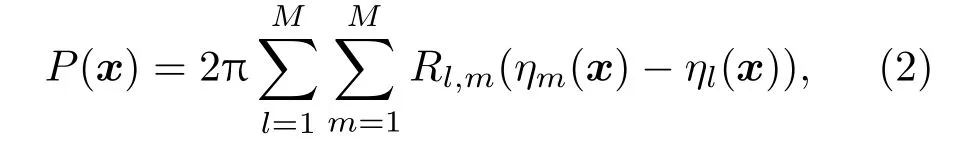
其中，ηm(x)∈R 表示第m个传感器的导向时延函数，即声信号从空间点x到第m个传声器的传播时间。在一般的声源定位应用中，传播模型通常简化为自由场中匀速传播，即

其中，v表示声速，“||.||”表示欧式距离。

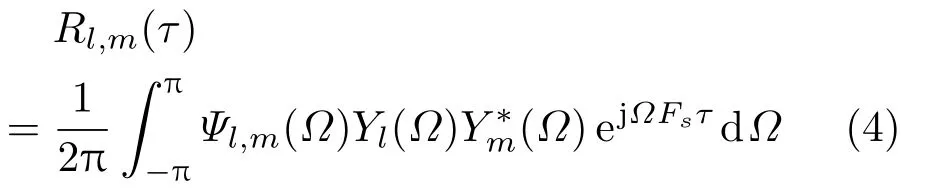
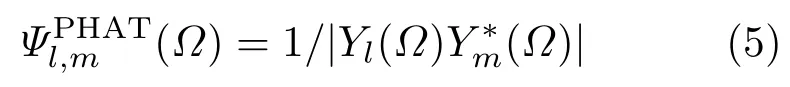
表示传感器对{l,m}间的GCC 函数，τ表示传感器对{l,m}间的时延，上标∗表示共轭运算，Ψl,m(Ω)表示GCC的加权函数。相位变换(Phase transform,PHAT)权重函数是时延估计和SRP应用中最常见的权重函数。利用PHAT 加权的广义互相关通常简称为GCC-PHAT，使用GCC-PHAT进行定位的SRP函数通常简称为SRP-PHAT。在理想条件下，SRP 函数亦将在声源位置xs处取得最大值，如图1(a)所示。

在传声器网络场景下，P(x)函数存在较多的局部极值，常用方案是对候选空间区域进行网格搜索的方式实现定位估计，在格(On-grid)定位结果可表示为

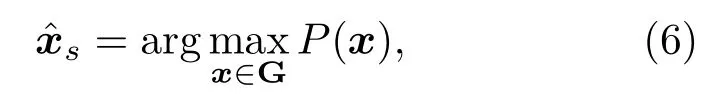
式(6)中，G表示网格采样的采样点集合。

1.2 导向时延不确定项

在实际系统中特别是在户外环境下容易受到环境因素的影响，计算SRP 函数用到的导向时延函数无法做到完全精确，即ηm(x)≠(x)。(x)∈R 表示声音从位置x到第m个传感器的实际传播时间，用

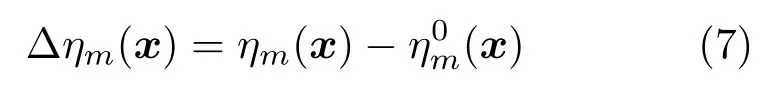
表示导向时延函数中的不确定项。将式(7)带入式(2)并移除式中与定位无关的传感器对{m,m}的自相关项和传感器对{m,l}&{l,m}中的重复项，SRP 函数中具有定位作用的空间函数可进一步简化为

其中，p表示传声器对cp={l,m}(l < m)的顺序标识，τp(x)=ηm(x)−ηl(x)表示导向TDOA函数，(x)=(x)(x)表示实际的传感器间信号延迟TDOA，∆τp(x)=∆ηm(x)−∆ηl(x)表示导向TDOA函数的不确定项。

由式(8)可知，SRP 空间谱是由p个传声器对的GCC 函数Rp(τ)到空间的投影叠加形成。声源位置xs处所有的GCC 函数均为峰值，因此形成汇聚的焦点区域。将式(1)带入式(4)可以将GCC 分成信号成分(自相关函数)和噪声成分：

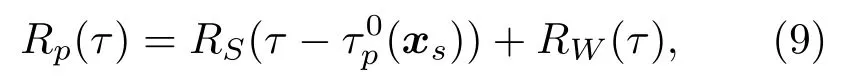
其中，RS(τ)表示信号的自相关函数，RW(τ)是信号和噪声的相关项和噪声的自相关项，信号在PHAT权重下的自相关函数为sinc 函数[19]。GCC 函数如图1(a)所示，蓝色线条为信号成分，可以看到其能量几乎完全集中在τ=τ0p(xs)附近，相比之下源自噪声成分RW(τ)用红色线条表示没有明确的指向性，能量呈均匀分布。∆τp(x)会使得Rp(τ)取值发生偏离，在τ=τ0p(xs)两侧的狭小区域内仍然有RS(τ)≫RW(τ)，τp(x)距离τ0p(xs)较远时RS(τ)与RW(τ)取值接近，此时可认为Rp(τ)丢失了空间函数中的声源信息。如图1(b)所示，实线为没有导向TDOA 函数不确定项时Rp(τ)的峰值区域，即τp(x)=τ0p(xs)对应的区域，声源xs用符号“O”表示，在该区域内部。存在∆τp(x)时实线区域Rp(τ)的取值湮没于噪声，而在如虚线所示τp(x)=τp(xs)对应的区域，Rp(τ)取到最大值，表现为Rp(τ)的峰值区域偏离了声源xs。对于不同节点对来说∆τp(x)的取值不同，因此偏离的程度也不一样，峰值区域各自相交形成了小的汇聚点，最终得到了散焦的SRP 函数，如图1(c)所示。在经典的SRP 函数应用场景，如基于声阵列的声源测向和室内多传声器定位中，∆τp(x)小到几乎可以忽略不计，因此通过SRP 函数的最大值仍然可以正常定位到峰值位置，如图1(d)所示。

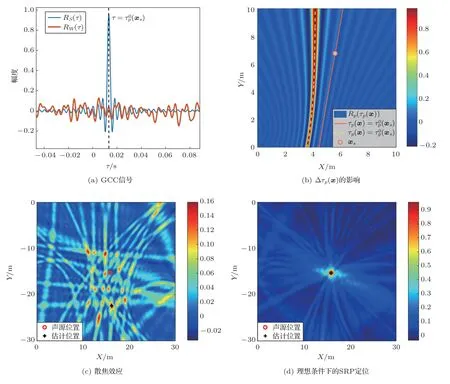
图1 基于SRP 函数的声源定位Fig.1 Illustrations of SRP-based localization

2 定位算法

2.1 导向时延不确定项的量化

导向时延不确定项∆ηm(x)的来源包括采样同步误差∆ts，节点的自定位偏差∆zm，空间离散化网格采样量化误差和不准确的传播模型。传感器网络的同步误差和自定位误差参数可从设备相关指标获得，|∆ts|≤σs，|∆zm|≤σL。格点xg ∈G代表的区域可记为

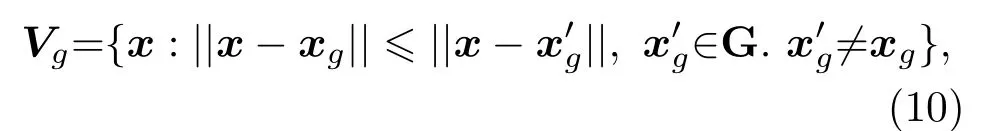
即所有到xg距离比到其他网格点更近的点的集合，量化误差∆zg=||x −xg||不大于网格的外接球半径，对于间距为r的N维方格有传播模型不确定性可以通过在声速上设定一个扰动项∆vm的方式进行建模，忽略地形的影响考虑温度误差∆T和风速u，那么|∆vm|≤∆v=0.6|∆T|+|u|。采用式(3)作为传播模型并带入以上各种因素，时延不确定项可表示为

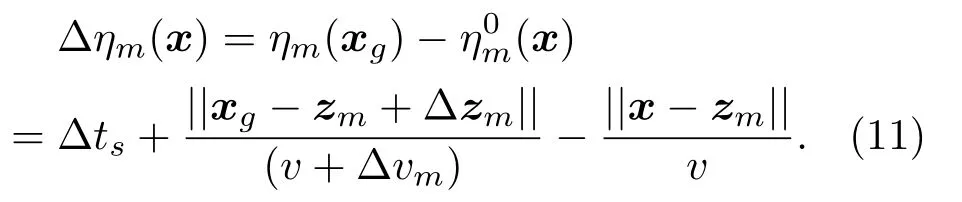
忽略二阶及以上小量，∆ηm(x)可以写成几个相互独立的子项：

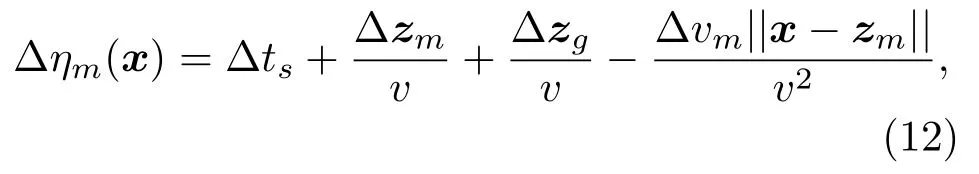
带入各因素的范围∆ηm(x)的上界可写成

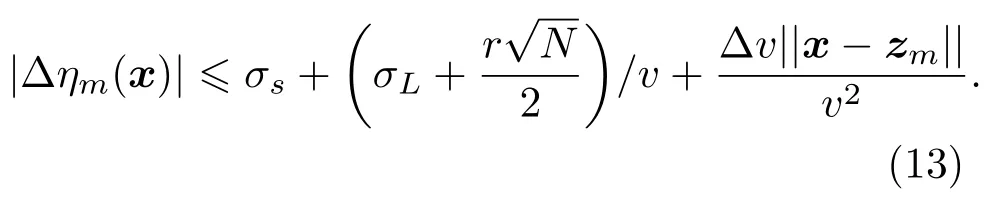
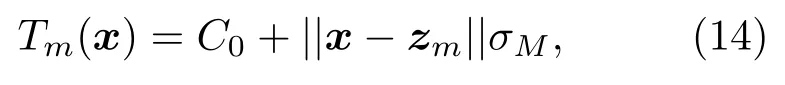
其中常数项

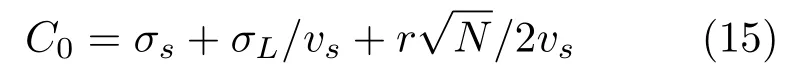
代表包含节点采样同步误差、自定位偏差和网格干扰等因素引发的时延不确定项量化上限；距离相关项中乘数项

代表以声速误差形式建模的传播模型误差引起的干扰，σM和传播距离的乘积即为传播模型误差引发的时延不确定项量化上限。

在式(8)中发生作用的导向TDOA函数不确定项∆τp(x)是两个传声器{l,m}的导向时延不确定项的叠加，令Dp(xg)=max{|∆ηm(xg)−∆ηl(xg)|}表示∆τp(x)的上限，考虑到传声器l和m的位置关系，Dp(xg)的向量形式为

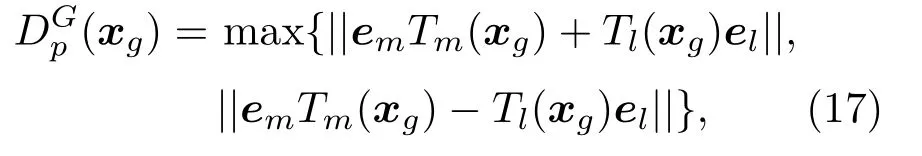
式(17)中，em=(zm −x)/||zm −x||表示传感器m对应的空间方向向量。

2.2 定位算法

MSRP 算法[22]考虑并分析了网格量化误差对导向TDOA函数τp(x)的影响，通过对GCC-PHAT进行区间求和的方式提高了SRP 算法的稳定性，MSRP函数可表示为

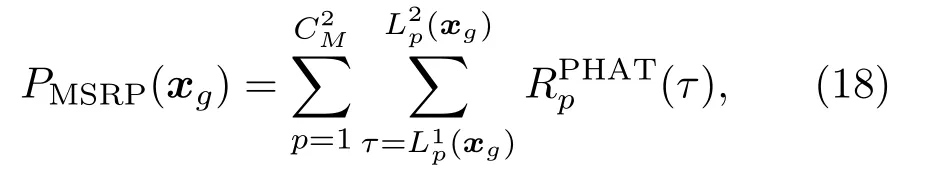
其中，(τ)表示GCC-PHAT 信号，(xg)与(xg)分别表示网格点处导向TDOA 的浮动下界和上界，对于方形网格，文献[22]中通过

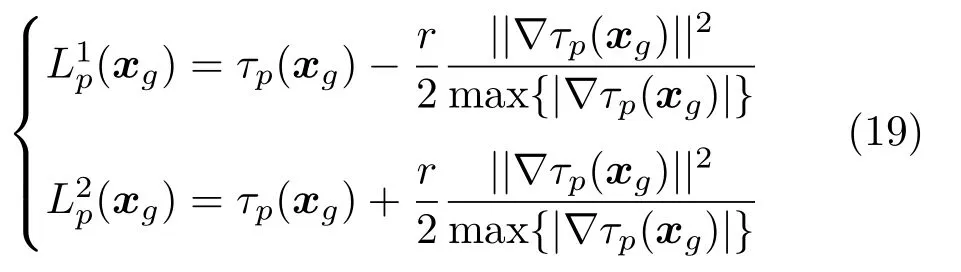
进行求解，其中，

表示导向时延TDOA函数τp(x)在网格中心处的梯度向量。式(19)计算的求和范围仅考虑了网格量化误差的影响，因此当时延不确定项所引起的扰动超过这个范围的时候，MSRP 函数仍然会产生散焦现象。

根据2.1 节中的分析，MSRP 函数中TDOA 的求和区间，在网格量化误差之余也应该覆盖导向时延不确定项中其他因素的影响。由此改进的MSRP2 算法调整了GCC-PHAT的求和范围，可以增强对导向时延不确定项的抗干扰性。将修正后的求和上下界

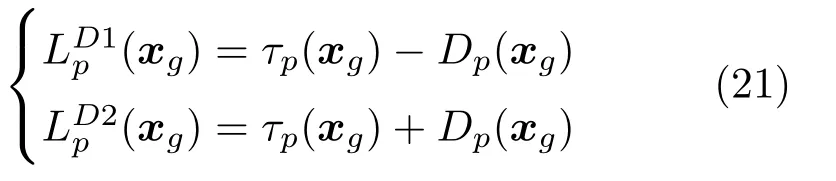
带入到式(18)中，得到修正后的MSRP2 算法的定位函数

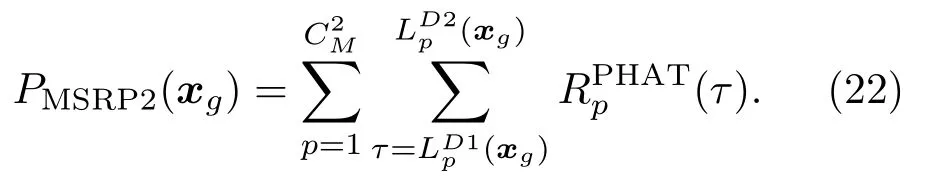
实际应用中在有限的区间范围内求和，噪声项在经过平滑之后仍然具有随机性，因此在低信噪比情况下，该方法容易失效。为保证SRP 函数在导向TDOA 存在不确定项的条件下仍然能够在声源最近的网格处取得函数最大值，提出了GCC最大值滤波(GCC maximum filter, GMF-SRP)算法，在计算每个网格点处的GCC 时，搜索Rp(τ)在[τp(xg)−Dp(xg),τp(xg)+Dp(xg)]范围内的最大值作为Rp(τp(xg))的取值。

GMF-SRP算法的函数可以表示为

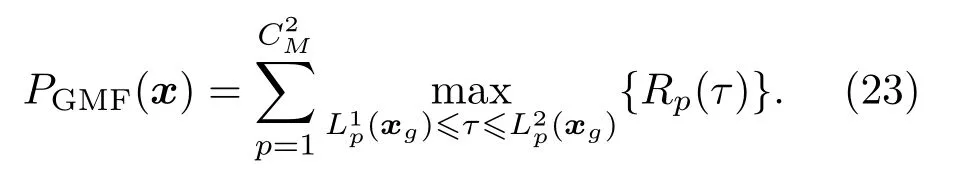
采用最大值滤波之后，空间函数在声源附近可能存在不止一个最大值点，计算所有取得函数最大值的网格的中心位置作为最终的定位结果。

算法流程如下：

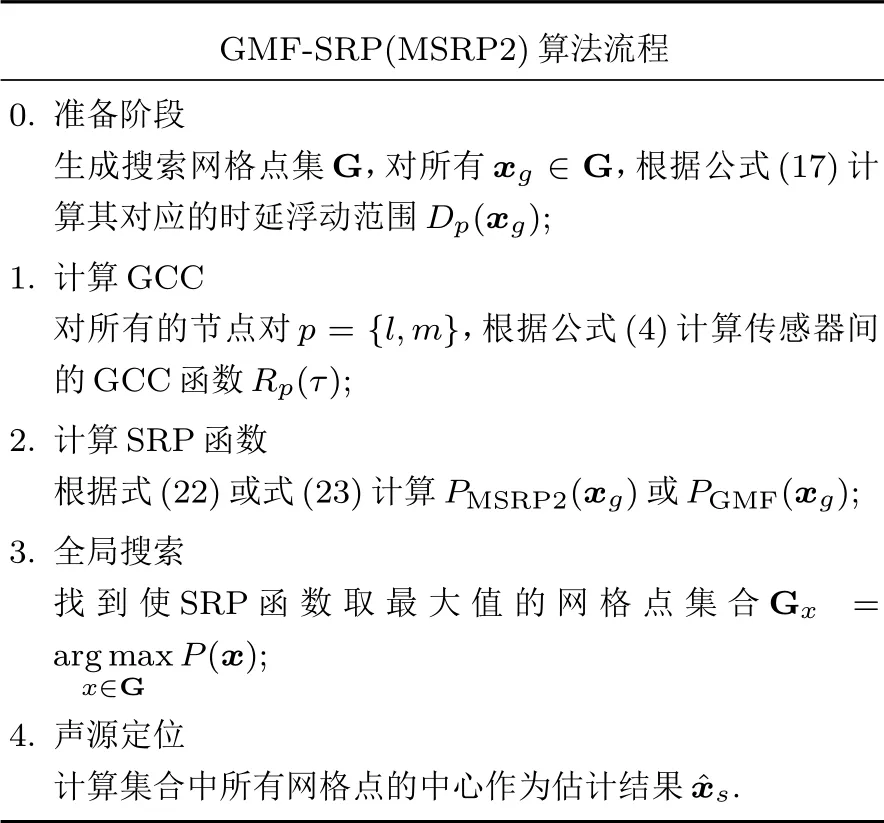
GMF-SRP(MSRP2)算法流程0.准备阶段生成搜索网格点集G，对所有xg ∈G，根据公式(17)计算其对应的时延浮动范围Dp(xg);1.计算GCC对所有的节点对p = {l,m}，根据公式(4)计算传感器间的GCC 函数Rp(τ);2.计算SRP 函数根据式(22)或式(23)计算PMSRP2(xg)或PGMF(xg);3.全局搜索找到使SRP 函数取最大值的网格点集合Gx =arg max P(x);4.声源定位计算集合中所有网格点的中心作为估计结果ˆxs.x∈G

2.3 性能分析

图2 给出了一组仿真的GCC-PHAT 信号，真实的Rp(τ0p)用倒三角符号表示，距离声源位置最近的网格点计算出的Rp(τp(xg))用正三角符号表示，导向TDOA 不确定项的范围用虚线框标出。从右边的局部放大图中可以看到由于导向TDOA 存在偏差，网格点的GCC 取值与真值相差很大。MSRP和MSRP2 算法是在框内求和，只要真值在范围内，求和之后就不会漏掉峰值。MSRP仅考虑了网格这一个因素，对应的虚线框范围小；MSRP2 算法和GMF-SRP 虚线框的范围更大，因此更加不容易漏掉真值。考虑到在有限的框内进行累加操作对噪声项的抵抗能力有限，求和之后的结果有可能受到噪声的影响。因此GMF-SRP 算法没有采用累加的方法，而是使用了噪声抑制能力更强的最大值滤波，在这种情况下虽然网格点的GCC 取值会因为导向TDOA不确定项的影响而发生偏离，但是只要实际的偏移量∆τp(x)在预估的Dp(xg)以内，也就是虚线框内包含τ0p时刻，GCC也会取到最大值。这样一来就有效拓宽了图1(b)中Rp(τ)的峰值区域，可以将真值附近图1(c)所示散焦的点汇聚在一起。GMF-SRP 算法的缺点是很多个网格都是最大值，会限制焦点区域内部的分辨能力。

图2 导向时延不确定项对GCC-PHAT 信号的影响Fig.2 Steering time delay uncertainty of GCC-PHAT

接下来分析算法复杂度，传统CSRP 算法是对每一个节点对计算GCC，然后遍历每个网格点计算所有节点对的和，MSRP 和MSRP2 算法是在每个网格点处，计算每个节点对在该网格点导向TDOA的范围，对范围内的GCC 求和作为该位置该节点对的值。GMF-SRP 是计算出网格点的导向TDOA的范围之后，对范围内的GCC 找最大值作为该位置该节点对的值。以上算法在计算GCC 和最大值位置的步骤计算量是一致的，在全局搜索时，设空间中网格数量为Ng，已知节点对数为C2M，因此CSRP 函数的计算量为O(NgM2)。MSRP 函数在每次GCC 的取值中增加了一次求和的过程，每个节点对在每个网格点处的范围内平均包含Nr个数值，计算量为O(NgM2Nr)。MSRP2 和GMF-SRP中累加与求最大值的计算量基本一致，区别在于考虑了导向时延不确定项之后，扩大了Dp(xg)，将Nr扩大到了NR，所以MSRP2 和GMF-SRP 的计算量约为O(NgM2NR)，复杂度与MSRP 保持在同一量级，计算量的增加取决于应用场景中导向时延不确定项的范围。

3 仿真分析

3.1 场景设计

仿真测试模拟室外分布式传声器网络的典型应用场景，利用蒙特卡罗实验分析GMF-SRP 和MSRP2两种定位算法的有效性，并与传统的CSRP算法[13]和MSRP 算法[22]进行对比。监控区域设置为边长为200 m 的正方形，在区域内设置了1 个声源和8 个传声器，用蒙特卡洛法随机生成了1000组传声器和声源的位置。声源信号采用功率为Ps的高斯信号，信号功率90 dB，传声器接收的信号由声源信号进行时间延时和幅度衰减后叠加上功率为Pn的白噪声获得，其中幅度衰减设置为球面传播衰减，时延项ηm(x)在直线传播时间的基础上叠加了用于模拟系统固有时延偏差的常数项和与用于模拟传播模型影响的与距离相关项，即tm=||zm −x||/v+∆tC+∆tM，其中常数项∆tC在[−C0,C0]区间内均匀分布，与距离相关项∆tM在[−σM||zm −x||,σM||zm −x||]均匀分布。在生成信号后，在网格间距为1 m 的条件下分别用4 种SRP 算法进行定位估计，统计各算法的估计误差的平均值(Mean absolute error, MAE)进行比较。

3.2 信噪比的影响

实验1 验证算法性能与信噪比的关系，Pn从35 dB增加到65 dB，模拟从安静环境到嘈杂环境的不同状态。依据声源到各传声器的距离不同算得接收端平均信噪比从11 dB下降到−19 dB。系统固有偏差C0为0.1 ms，传播模型影响σM为0.05 ms/m。

表1 和图3 给出了不同信噪比下4 种定位方法估计误差的平均值对比。从结果中可以看出，当平均接收信噪比高于−4 dB 后，各算法的计算结果没有显著的变化。根据公式(9)，信噪比足够高时，噪声项RW(τ)不影响信号分量RS(τ)在何时取到最大值，此时定位误差可以认为与信噪比无关。随着信噪比降低，信号分量逐渐被噪声湮没，定位误差逐渐增大。传统算法CSRP 在高信噪比(>10 dB)时也无法获得有效的定位结果，这是由于室内应用时网格间距通常不超过5 cm[22]，使得其无法应对1 m的网格间距。在仿真中的监控区域，受到计算机计算能力和内存限制，无法采用厘米级别网格进行搜索，CSRP 算法难以适用。区域求和类算法(MSRP和MSRP2)在−9 dB后开始显著变差，信噪比足够支持有效定位的情况下MSRP2 算法的平均误差小于MSRP 算法。GMF-SRP 的平均误差始终保持最小，并且在−14 dB 以上均保持了稳定的定位性能，显示更强的噪声抑制能力，可以适用于信噪比更低的环境。

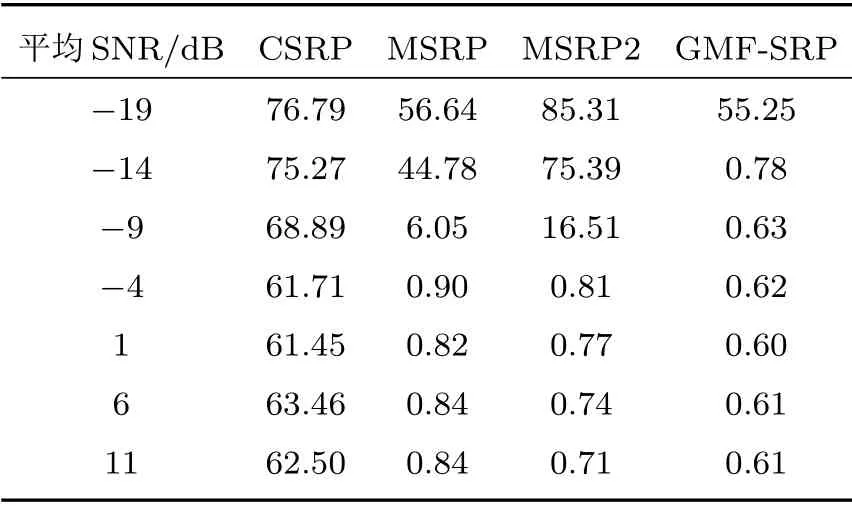
表1 平均接收端信噪比对MAE 的影响Table 1 The MAE comparison under average receiving SNR(单位: m)

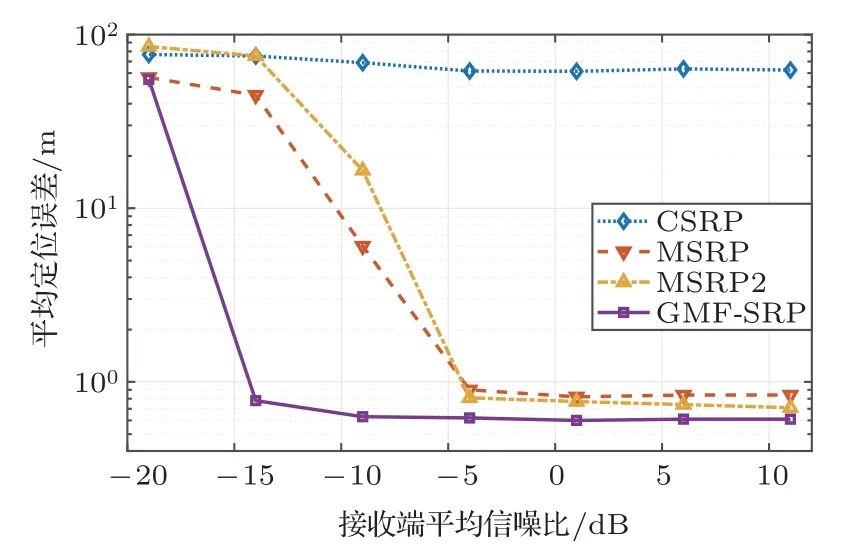
图3 平均定位误差随信噪比变化曲线Fig.3 Average localization error with signal to noise ratio

3.3 量化参数的影响

实验2 分别验证了导向时延不确定项中的量化参数中常数项C0和乘数项σM的影响。首先设置C0为0.1～10 ms，等效为定位系统存在约3 cm、30 cm 和3 m 的节点自定位误差，平均接收端信噪比1 dB，σM为0.05 ms/m。

此时MAE 对比结果如表2 和图4 所示。由于网格限制CSRP 算法只能得到发散的结果，其他算法的定位偏差也会随着时延偏差量增大而稍有增大。10 ms 相较于1 ms 的情况，定位偏差的增加并不明显。在固定时延偏差量0.1～10 ms 的区间内，MSRP2和GMF-SRP 相比于MSRP 均提高了定位精度。在C0增大至10 ms 时，MSRP2 的作用不及GMF-SRP显著，说明区域最大值滤波的方法更优。

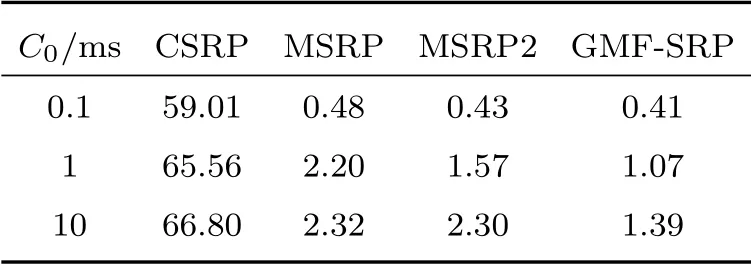
表2 C0 对MAE 的影响Table 2 The MAE comparison under C0(单位: m)

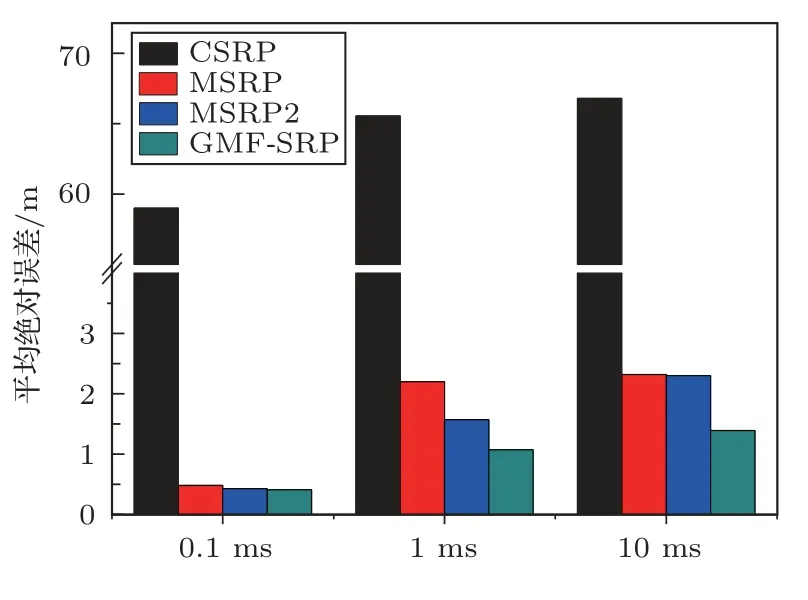
图4 C0 对定位误差的影响Fig.4 Influence of C0 on localization error

接着研究传播模型不准确的影响，乘数项σM最小为0.01 ms/m，模拟一级风，逐渐增加到0.05 ms/m、0.1 ms/m 和0.2 ms/m，分别等效于3级、5 级和8 级风。C0为0.1 ms，平均接收端信噪比1 dB。为了进一步观察传播距离的影响，还增加了边长为1000 m监控区域在不同条件下的结果对比。

仿真结果如表3 所示。从表格中可以看出随着σM的增大，所有算法的定位误差均会增加，MSRP2和GMF-SRP 算法相较于MSRP 算法的误差更小，同时可以看出区域扩大之后的传播模型不准确的影响也被放大。在所有情况下GMF-SRP 算法是平均误差最小的，在风速和区域更大的不利条件下有明显的优势。

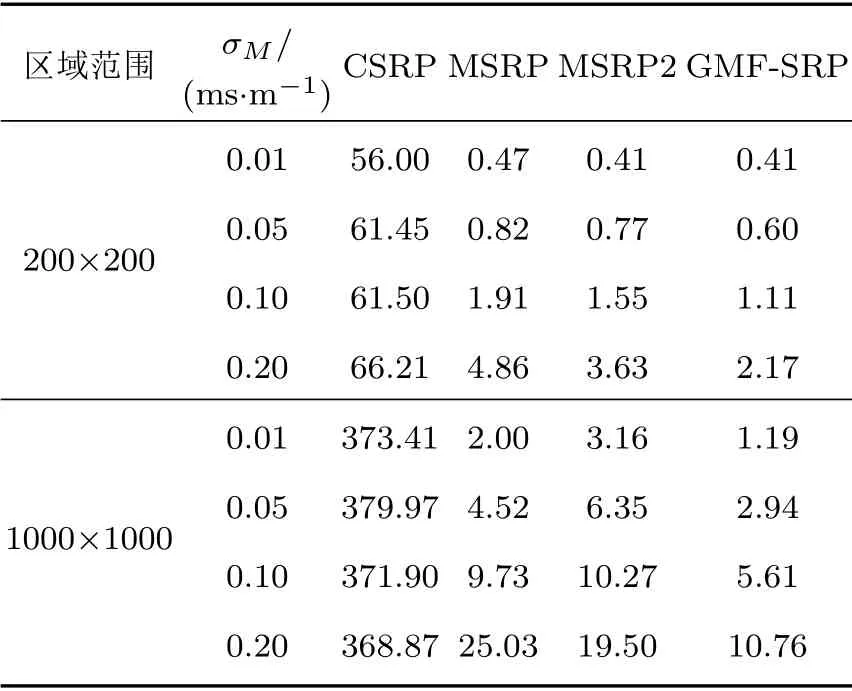
表3 σM 对MAE 的影响Table 3 The MAE comparison under σM(单位: m)

由于CSRP 已经彻底失效， 图5 中给出了σM= 0.05、区域边长200 m 时，另外3 种算法的SRP空间谱图对比，从图中可以看到MSRP算法中由于求和区域小，还是出现了散焦效应，因此定位误差相对较大。MSRP2 算法空间谱中峰值区域是集中的，GMF-SRP 的汇聚作用更明显因此定位效果最好。

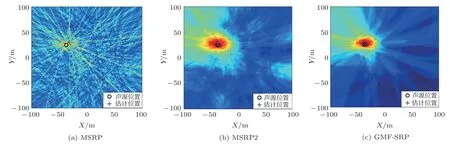
图5 SRP 对比Fig.5 SRP comparison

3.4 计算复杂度对比

取导向时延不确定项量化的常数项C0为1 ms，乘数项σM为0.05 ms/m。各算法在同一计算平台上的平均运算时间如图6 所示，CSRP、MSRP、MSRP2 和GMF-SRP 算法的平均计算时间分别为0.10 s、1.48 s、1.59 s和1.66 s。MSRP、MSRP2的求和运算和GMF-SRP 取最大值的计算相较于CSRP显著地增加了整体的运算量。MSRP2和GMF-SRP算法扩大了导向时延不确定项的范围，与MSRP相比计算量的增加并不明显。

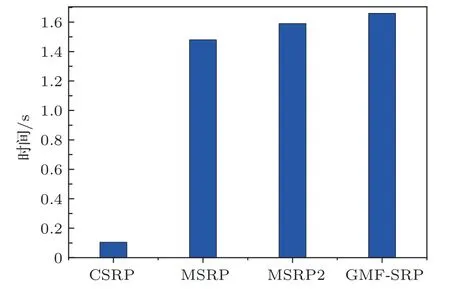
图6 不同算法的平均计算时间Fig.6 Average computing time of different algorithms

4 实验验证

4.1 场景描述

如图7(a)所示，在边长为200 m 的矩形户外区域内布设了7 个无线传声器节点(实景如图7(b)所示)。传声器采样率为10000 Hz。在场地内随机挑选了12个位置用移动传声器播放了白噪声、鸟鸣声和汽车鸣笛声这3 三种类型的声信号。节点加装全球卫星导航(GNSS)模块用于自定位和采样同步校准，同步误差为0.1 ms，自定位误差为1 m。实验当天的气象条件温度30◦C，风力等级为2～3 级，最大风速5 m/s。

考虑到室外环境噪声主要集中在低频部分，对接收数据进行了1500 Hz 以上的高通滤波处理，传声器的全频带信噪比和滤波后信噪比结果如图7(c)所示。可以看出，滤波后信噪比提升了20～30 dB。根据气象和设备信息，计算用的基本声速设置为349 m/s。式(14)中的常数项C0和乘数项σM分别设置为6.1 ms和0.05 ms/m。

图7 实验设置Fig.7 Setup

4.2 实验结果与分析

实验中共录取了1242 帧长度为2 s 的有效数据，采用4 种不同的算法对这些数据进行了定位估计，同时也验证了高通滤波处理下的定位结果。平均误差如表4 所示，从表中可以看出，经过高通滤波的信号提升了信噪比因此减少了定位误差。同时可以发现单纯地修改MSRP的求和区域，对于实际数据并没有起到减小误差效果。GMF-SRP 在全通或者高通条件下均显示出了稳定可靠的定位性能。

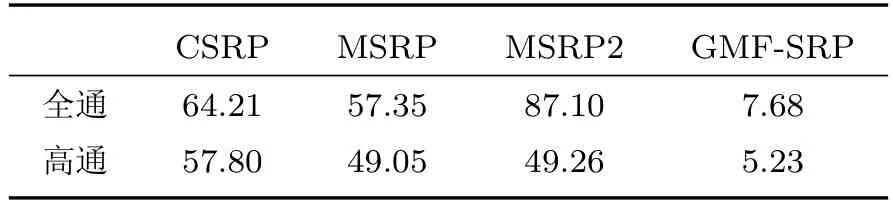
表4 实验结果定位估计平均误差对比Table 4 The MAE comparison of the field experiment(单位: m)

为了更全面地展示算法的稳定性，本文还给出了两种条件下定位误差的累积概率分布，如图8 所示。累计误差分布曲线越靠近左上角，也就是越早接近100%，估计出发散的结果越少，对应的算法稳定性越好。两张图中的曲线显示GMF-SRP 在稳定性方面要显著地优于MSRP 和MSRP2，以20 m 的误差距离为界，其他算法在全通条件下的误差小于20 m 的概率不到15%，高通条件下小于20 m 的概率不超过40%。对比两张图也可以看出，高通滤波提升信噪比之后在提高算法稳定性方面也有一定的作用。

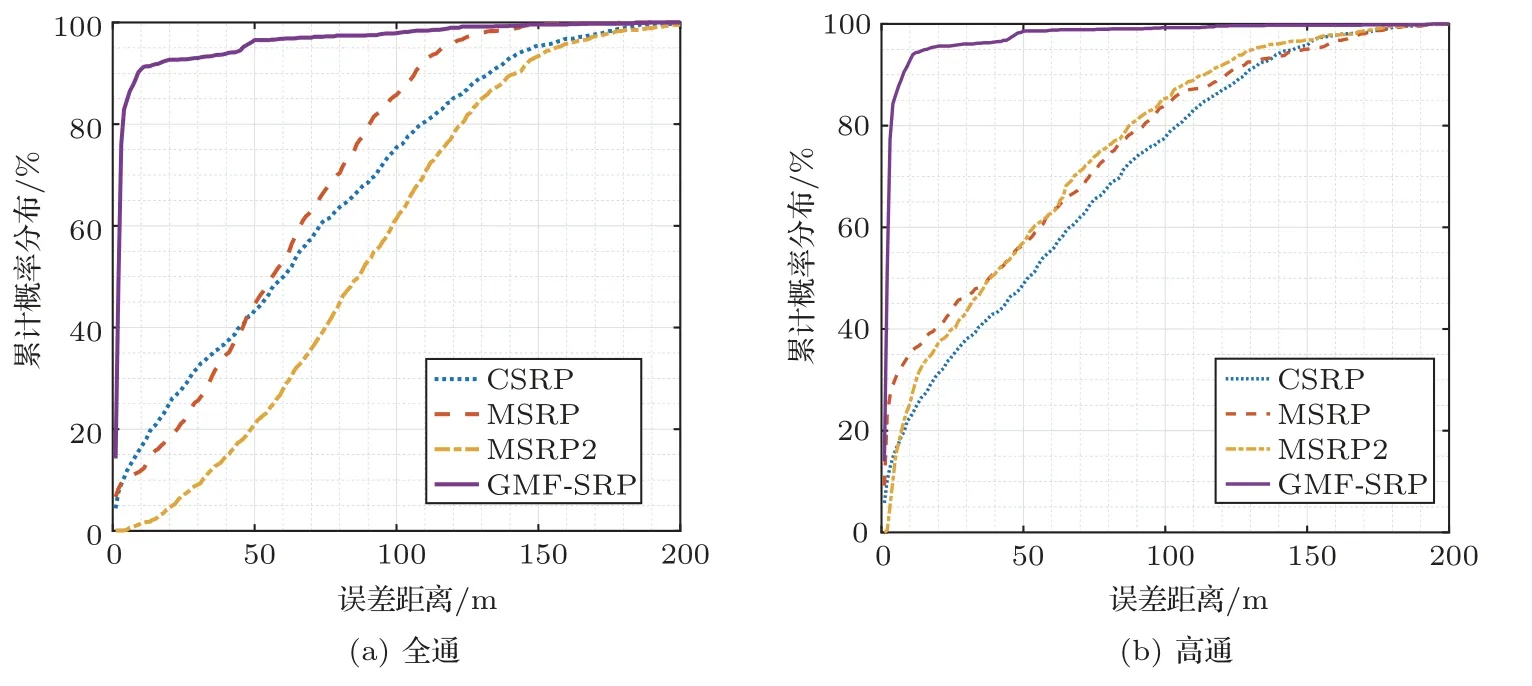
图8 定位误差累计概率分布Fig.8 Cumulative distribution function of localization error

图9 给出了实验数据全通条件下4 种算法的SRP 图，图中“十”字表示估计的声源位置，圆圈表示声源的真实位置。CSRP算法的SRP图杂乱没有峰值区域。MSRP算法得到的图中出现了分散的交汇产生的亮点区域，不足以得到可靠的定位结果。MSRP2 函数扩大了求和范围，SRP 图更加平滑，但是在实验的信噪比条件下，仍然无法给出正确的定位结果。GMF-SRP算法解决了散焦效应问题，在整个图中有唯一的高亮区域。

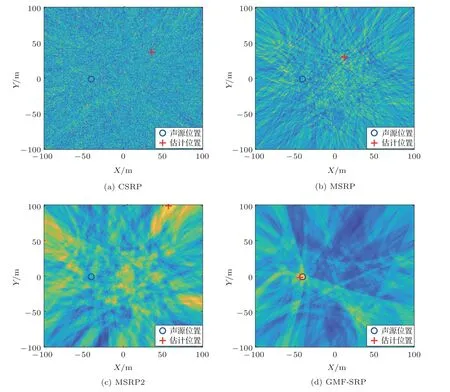
图9 实际数据SRP 图Fig.9 SRP map of real data

5 结论

在分布式声传感器网络场景下利用SRP 算法进行声源定位，由于传感器采样不同步、节点自定位误差和传播模型不准确的影响，SRP 函数中的导向时延函数存在一个不确定区间从而导致定位结果出现发散的情况。本文在SRP 模型中引入了导向时延不确定项，对引发导向时延不确定项的主要干扰因素进行了分析并量化了不确定项的变动范围，在此基础上改进了MSRP 算法的GCC 求和累加范围，并提出了基于最大值滤波的GMF-SRP 算法，MSRP 函数的改进算法中，其求和累加范围覆盖了导向时延引起的导向TDOA 变化区间；GMFSRP 算法对位于导向TDOA不确定项区间的GCC进行最大值滤波，并以之替代SRP 函数中的GCC从而提高算法的稳定性。仿真结果显示，GMF-SRP算法具有更强的抑制噪声作用，MSRP2 算法和GMF-SRP算法均可以减小定位误差，MSRP2算法和GMF-SRP 算法相比于MSRP 算法并没有显著增加计算量。野外实验数据表明，GMF-SRP算法能够有效提高定位精度和稳定性。