利用微分求数量函数对矩阵变量的导数

杨衍婷

(咸阳师范学院数学与统计学院，陕西咸阳 712000)

近年来，伴随着计算机和信息科学的飞速发展，矩阵分析理论的应用日益广泛，而矩阵求导是矩阵分析理论中的重要问题，特别是常见的数量函数对矩阵变量的求导问题,在研究优化等问题时起到关键作用。文献[1-4]讨论了矩阵求导的一些方法。在文献[4]的基础上，具体分析了利用矩阵微分的性质以及微分和导数的关系求数量函数对矩阵变量的导数，与按照矩阵导数的定义求导相比较，运算更加简单，可操作性更强。

1 矩阵导数和微分的定义

定义1设f(X)是以矩阵X=(xij)m×n为自变量的元mn函数，且

定义2设矩阵F(X)=(fij(X))s×t的元素fij(X)(i=1,2,…,s;j=1,2,…,t)都是矩阵变量X=(xij)m×n的函数，规定F(X)对矩阵变量X的导数为

由于矩阵可以拉伸成向量，即若

X=(xij)m×n，则

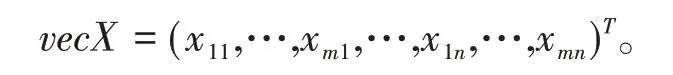
在文献[4]中，矩阵值函数的微分定义是将函数矩阵和自变量矩阵拉伸为向量。

定义3设矩阵值函数f(X)=(fij(X))s×t，

以向量X=(ξ1,ξ2,…,ξn)T为自变量，f可微，则

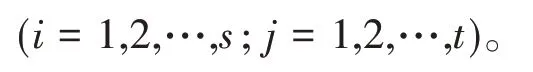
当函数自变量为矩阵时，继续采用文献[4]中的方法，将自变量矩阵拉伸为向量，而当函数值为矩阵时，采用定义3，函数矩阵各个分量元素分别微分，而不将其拉伸为向量，便于数量函数对矩阵变量求导计算。

2 矩阵导数和微分的相关结论

根据矩阵微分的定义，若是U,V矩阵值函数，A是常量矩阵，则

基于文献[4]，按照定义3，总结出以下结论。

命题1设矩阵A=(aij)m×n，n维列向量X=(ξ1,ξ2,…,ξn)T，微分df=AdX，则

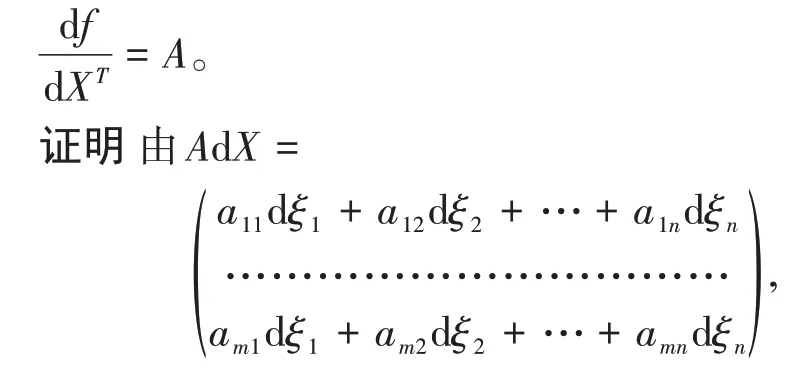
从而根据定义2可得。

命题2矩阵A=(aij)m×n，X=(xij)m×n，若微分

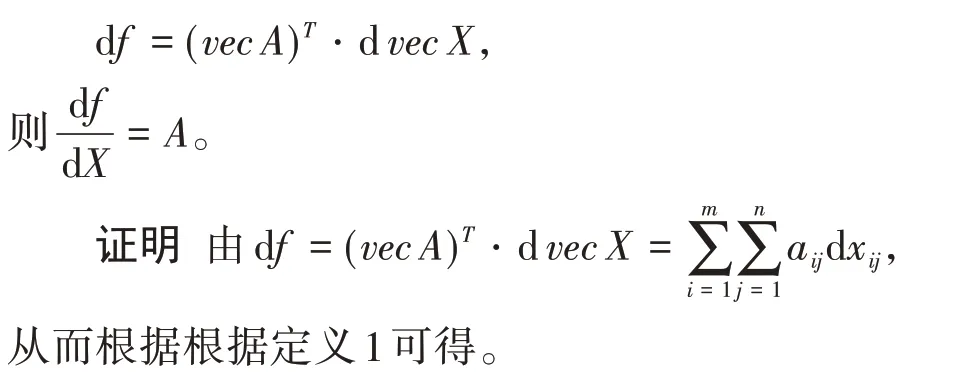
常用的以矩阵作为自变量的数量函数主要有3种：（1）二次函数；（2）迹函数；（3）行列式函数。为了对这3 种数量函数关于矩阵变量求导，给出以下命题。

命题3F是非奇异矩阵函数，则微分

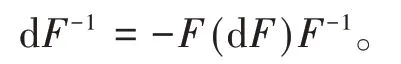
证明 根据

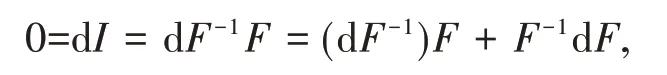
可得dF-1=-F-1(dF)F-1。

命题4是非奇异矩阵函数，则微分，

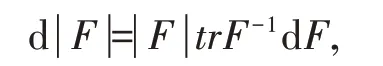
其中，|F|是F的行列式。

证明参阅文献[4]，根据定义1，定义3可得。

3 应用举例

例1设列向量x∈Rn，若A∈Rn×n，则

4 结语

分析总结了利用矩阵微分的性质以及矩阵微分和导数的关系求数量函数对矩阵变量的导数，大大简化了按照矩阵定义求导的过程，降低了矩阵求导的难度，并且使得矩阵求导具有了较强的可操作性。