无人机航迹规划算法

张 婷，鱼小军，帅 欢，刘 闯，朱豪坤

（湖南云箭集团有限公司，湖南长沙 410100）

无人机是指在不需要人员操作的情况下，能够依据自身对周围环境的感知、理解，自主进行运动控制，且能达到人类的驾驶水平的飞机。无人机因其具备低成本、适用场景多、无人员伤亡等优点，已成为世界各国为适应未来战场需要而重点研究的内容。

近年来，随着机器学习和强化学习理论的发展，无人机领域也掀起了一场人工智能变革。为保证无人机顺利完成任务且代价付出最小，需要运用合理高效的规划算法，使无人机在众多约束条件下获得航迹评价函数的最优或次优解，以确保无人机的航线质量。

下面对当前常用的几种规划算法进行分类，分析其优缺点，并提出无人机航迹规划算法面临的挑战和未来发展趋势。

1 航迹规划算法

无人机的航迹规划是指通过执行一系列的动作，在完成任务的前提下，生成无人机的最优/次优路径。航迹规划本质上是由在有限空间规避障碍的一系列点组成有向图的过程，航迹规划算法就是该过程的核心。

本文梳理了针对不同场景所需使用的算法，并根据搜索方法建立不同的模型与算法原理。将无人机航迹规划算法分为5 类，分别为基于控制理论的优化算法、基于单元分解的搜索算法、基于图论的规划算法、基于局部搜索的规划算法和基于全局搜索的规划算法，如图1所示。

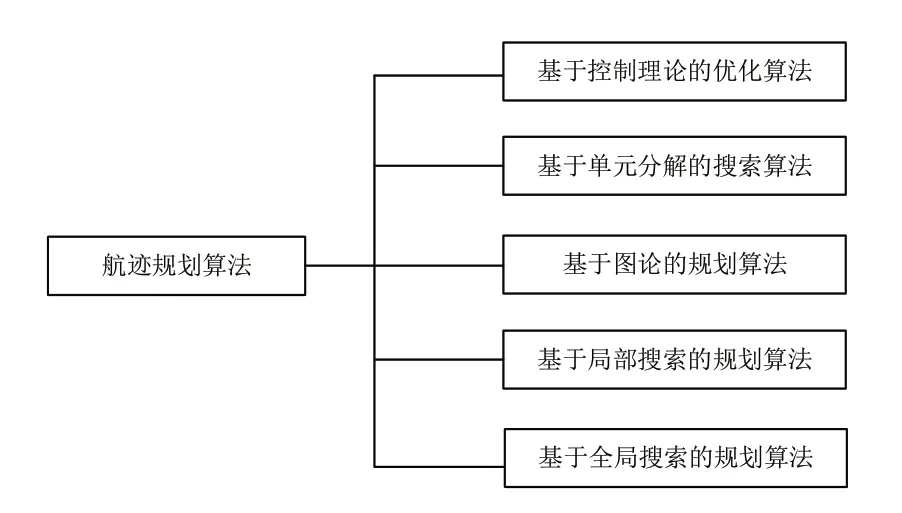
图1 航迹规划算法层次图Fig.1 Hierarchical chart of track planning algorithm

1.1 基于控制理论的优化算法

基于控制理论的优化算法主要分为只需使用目标函数求解的直接法和需要用导数求解问题的间接法2类。

直接法通常有模式搜索法、单纯形法和Powell方法。这些方法都不需要对目标函数进行求导，计算量和存储量都很小。模式搜索法是最简单的直接法，它与单纯形法都存在收敛速度慢的问题。使用共轭方向进行搜索的Powell 法与前2 种方法相比，收敛速度明显加快，但编程却比较复杂。

间接法有沿负梯度方向搜索的最速下降法，把求解复杂Hesse矩阵转化为求解一阶导数的牛顿法和求解正定系数矩阵的共轭梯度法等。最速下降法有3个特点：1）函数下降速度随着靠近极小点而变慢；2）每1次迭代都是沿当前处函数值下降最快的方向；3）当目标函数等值线为同心圆族或同心椭圆族时，1 次一维搜索就可得到最小点。最速下降法虽不再具有实用性，但许多有效的算法都是在其基础上加以修正并得到的。牛顿法和最速下降法都是迭代法，其基本思想是最优路径的特性用多目标代价函数的远离函数形式表示，求解导数为0的点作为迭代点，不断求解新的迭代点，重复上述步骤直到达到终止条件，即得到最优解。用于求解正定系数矩阵线性方程的共轭梯度法是目前使用最为广泛的优化方法之一，它比最速下降法收敛速度快，比牛顿法节约存储空间且稳定性高，无须外来参数。

基于控制理论的优化算法都是一些基本算法，虽在无人机航迹规划中一般不会直接使用，但仍十分重要，许多的航迹规划算法都是在其基础上修正得到的。

1.2 基于单元分解的搜索算法

基于单元分解的搜索算法分为确定型搜索算法和随机型搜索算法。常用的确定型搜索算法有动态规划法（Dynamic Programming，DP）、A*算法和D*算法等。

DP 算法的基本思想是将原问题进行不同程度的分解，由子问题的解层层递进求解下一级问题，重复该步骤直到得到最优解。因此，在动态规划算法中我们需要“缓存”这些解，以避免因重新计算它们而出现无法满足实时性要求的问题。孙健等人提出采用切线法的基于动态规划的无人机实时航迹规划算法，在满足约束条件的前提下，该算法不仅实时性好，还能生成平滑有效的航迹以规避威胁。

A*算法是基于启发式搜索和最短路径搜索相结合的算法，一般应用于二维空间的搜索。其思路是基于在1 张图上找到起点（star）到目标点（goal）之间的最优路径（path）。其之所以被定义为最佳优先算法，是因为在配置空间中的每1 个栅格都可以由A*算法的约束公式表示：

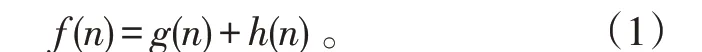
如图2所示，最优代价()就是图中A*算法的第1次遍历和第2次遍历的过程中，实际代价()和估计代价()取得的最优路径所需代价值。

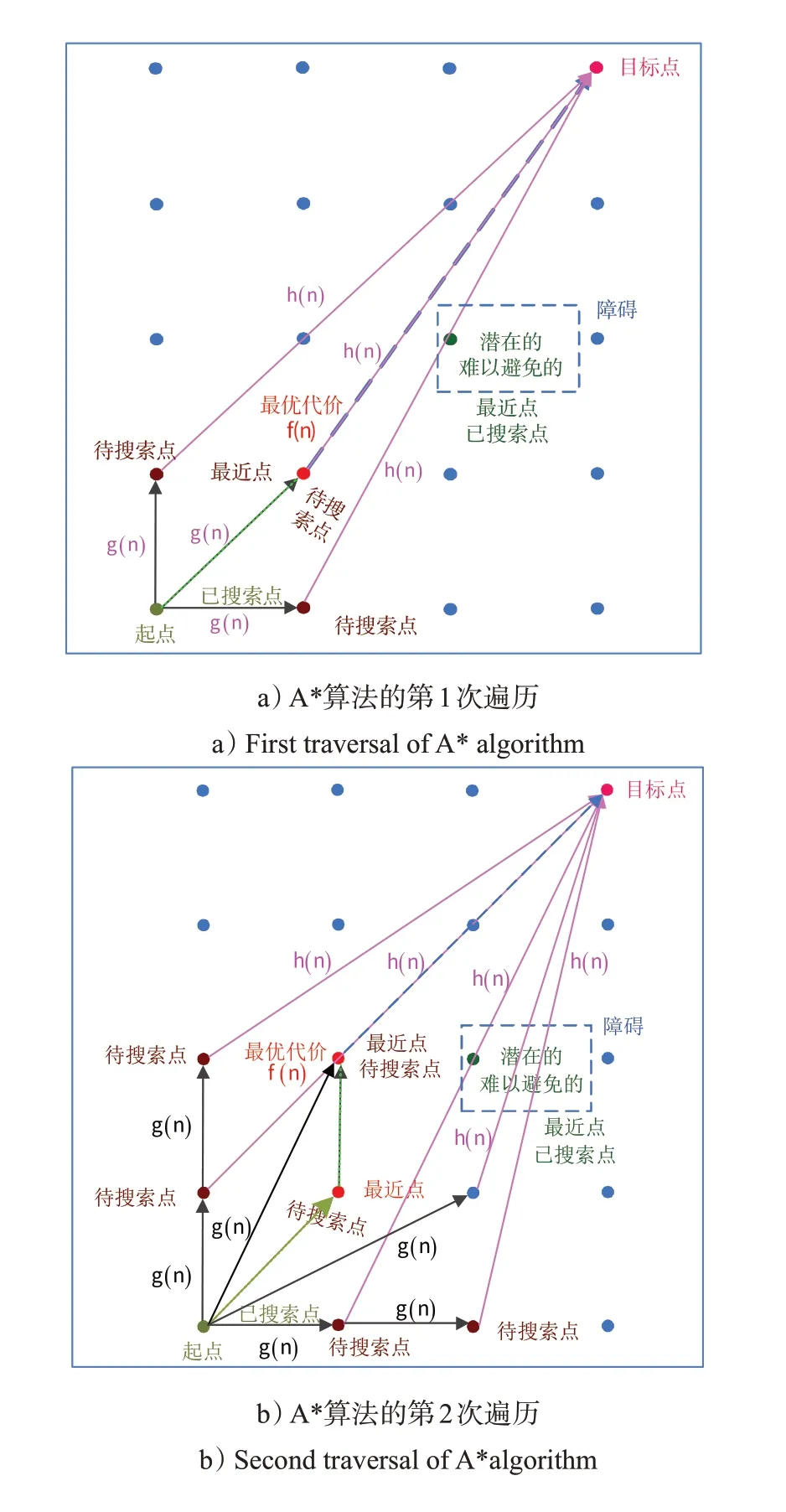
图2 A＊算法遍历过程图Fig.2 Traversal process diagram of A*algorithm

针对A*算法有易陷入局部最小值，随着搜索数据增大而增加搜索时间和实时性得不到保证的问题，杨玉提出能够利用较少内存得到1个代价低、较平滑、占存少的FSSA-SA 算法，该算法首先使用稀疏A*算法进行往返搜索，将得到的最优航迹作为模拟退火算法的初始解，然后用模拟退火算法去除冗余的节点，以此改善航迹质量。

普遍使用的随机型搜索算法有利用选择、交叉的遗传算法（Genetic Algorithm，GA），模拟人脑系统的神经网络算法（Neural Network Algorithm，NNA）和使降温带来能量差的降温概率趋向稳定的模拟退火算法（Simulated Annealing Algorithm，SAA）。

目前，GA算法在工程教育中得到了广泛的应用，作为学习和解决复杂问题的自适应技术，它是1 种用于解决混合计算挑战的元启发式方法。其核心是利用选择、交叉和变异算子有效地管理搜索系统策略，是1种支持随机搜索的智能应用，用历史数据来帮助搜索某一领域的改进覆盖范围框架内的结果。

人工神经网络是1 个松散模拟人脑的系统，它试图在专门的硬件或复杂的软件中模拟被称为神经元的多层简单处理元件。每1 个神经元根据不同强度的连通系数与它的某些邻域相连，神经网络学习是通过调整这些优势来实现的，并最终得到最优解。人工神经元的基本原理如图3所示，和是需要学习的参数，权重决定了神经元对输入的学习能力，偏置保证函数与原点的偏离距离。

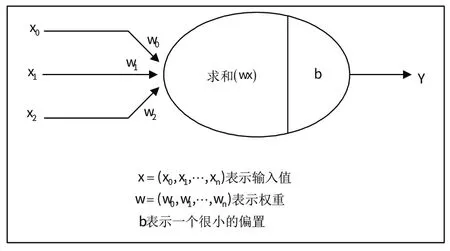
图3 人工神经元基本原理图Fig.3 Basic schematic diagram of artificial neuron

1.3 基于图论的规划算法

基于图论的规划算法有Voronoi 图法和快速搜索随机树法（Rapidly Random Tree，RRT）。

Voronoi图法是经典的航迹规划方法，它根据每条边的代价最终找到最优航迹。在这一领域虽已有许多成熟研究，但大多集中于对算法设计和实现的研究方面，而针对参数对整个算法性能影响的研究却很少。Voronoi图边线构成的航迹平滑度较低，通常在实际使用该航迹前还需要进行航迹平滑优化处理。针对动态环境下单无人机攻击多个移动目标的航迹规划问题，陈香敏根据事先了解的威胁分布构造Voronoi图，利用改进的Dijkstra算法得到最短路径。实践证明，该算法能有效地打击多个移动目标，且可缩小搜索空间和缩短搜索时间。

RRT算法具有搜索速度快，无须对任务进行空间建模的优点。其原理是从起点出发，在非障碍空间随机产生新节点，遍历所有节点到达目标点，找出其中最短的1 条路径。RRT 算法的前2 次遍历和找到的最优航迹过程，如图4所示。

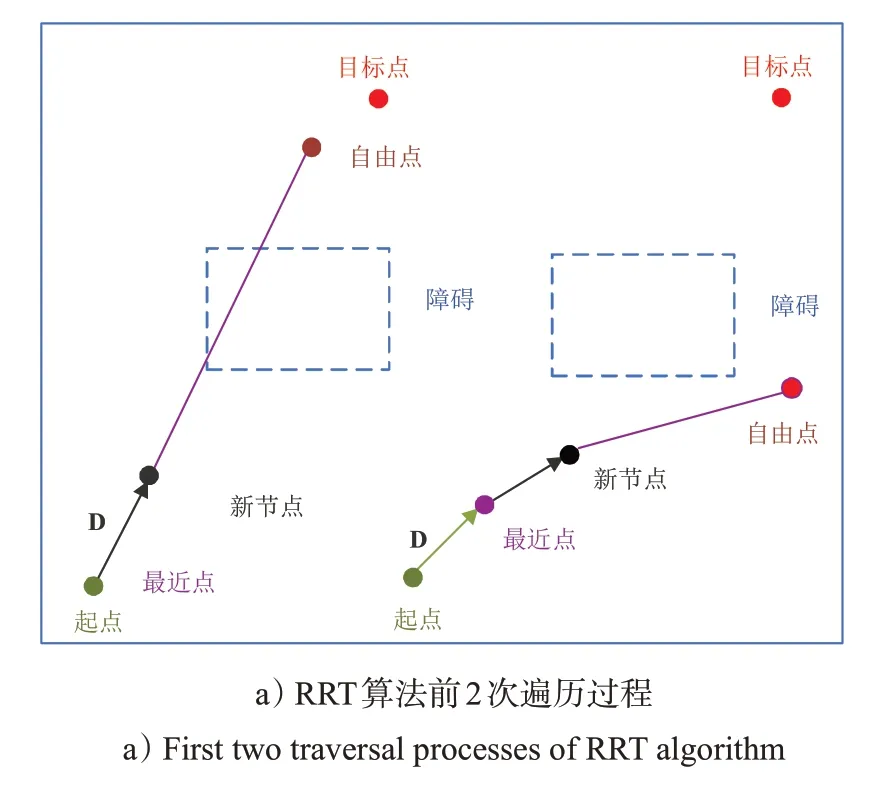
图4 RRT算法遍历过程图Fig.4 Traversal proess diagram of RRT algorithm

张伟民提出了基于目标约束采样和目标偏置扩展的改进RRT*算法。该算法每1 个新的自由点是由采样点和目标点所分配的权重共同决定的，通过仿真验证，它能使搜索速度加快，并能对搜索的航迹进行平滑处理。

1.4 基于局部搜索的航迹规划算法

局部和全局搜索广泛应用于无人机航迹规划中，局部搜索生成的航迹更平滑可飞，但易陷入局部最小，虽全局搜索能改善该问题，但存在搜索速度慢、占内存较大的不足。将两者相结合进行搜索：首先，根据已知条件采用粒子群算法或蚁群算法等全局搜索算法得到1条航迹；然后，根据无人机执行任务的实际情况，使用人工势场法或Dijkstra 算法等局部搜索对原航迹进行修正，能够得到最小代价下的最优/次优航迹。本文局部搜索算法主要介绍人工势场法和Dijkstra算法。

人工势场法是1种可解决局部规划问题的在线算法，其核心是构造引力势场函数和斥力势场函数，整个搜索范围是1 个势场，无人机对威胁产生的力起排斥反应，对目标点产生的力起吸引作用，无人机在合力（吸引力和排斥力的矢量和）的作用下运用，并最终到达目标点。该算法的在线规划体现在无人机先按照预先模型规划的路线飞行，在任务执行过程中，根据威胁对任务完成的影响程度，最终决定是否启动人工势场法对航迹进行在线修改。郭忠同通过改变斥力场来改进人工势场法，并对规划出的航迹进行平滑处理，能够避开威胁得到1 条满足约束条件且可飞行的最优路径。

Dijkstra 算法是1 种在图中寻找最短路径的图搜索算法，配置空间近似离散单元网格空间、栅格等。Dijkstra 算法的思路是：从起点出发，到其余点的最短路径，当通过另外1条路径再次遍历到这个节点时，由于该节点已经被遍历过，此时不再直接跳过该节点，而是对比当前的路径是否比该节点最初遍历的路径代价更小，若是，则将该节点纳入新的路径中，随即，该步骤不断重复，直到得到最优解。该算法是求解2点间最短航迹的最好算法，但存在易陷入局部最小值以及不必要的航迹转折使求得的航迹距离过长的问题。为了解决这些问题，王兰提出1 种远程曲面航迹全局静态规划方法，将Dijkstra 算法与模拟退火算法组合生成新的算法——Dijkstra-SA，该算法整体搜索效率和实用性好，能够高质量完成在线动态航迹规划。

除了上述2种算法，模拟退火算法、爬山法和遗传算法也可用于局部最优路径的搜索。局部搜索不关心路径的搜索，而是从当前1个单独状态出发，仅移动到最优相邻状态，虽收敛速度快，但易陷入局部最优解，不能满足无人机规划的全部约束条件，从而造成“一叶蔽目”的问题。

1.5 基于全局搜索的航迹规划算法

现代战场的打击目标和威胁环境不再单一，单无人机被击中后将会直接导致任务失败，故不再满足战场需求，而多无人机作战则是未来战争发展的必然趋势。局部搜索算法已不能满足多无人机的航迹规划，要解决该问题，须在局部搜索算法的基础上，提出全局搜索算法。本文通过介绍蚁群算法（Ant Colony Optimization，ACO）、粒子群算法（Particle Swarm Optimization，PSO）及它们的改进算法来了解全局搜索规划算法。

蚁群是根据“信息素”的浓度来找到最短路径，ACO 算法是1 种基于信息正反馈原理模拟蚁群群体行为的进化算法。针对无人机群体协同搜索任务规划问题，文献[34]提出了1 种基于人工势场的蚁群优化算法，该算法采用分布式结构，将每1个无人机进行自主决策，通过不断更新人工势场和信息素地图来得到新的搜索结果。通过不断重复该过程，实现了无人机群在航迹规划中的协同搜索，并通过仿真验证了该方法的可行性和有效性。由于ACO 算法存在易陷入局部最优解和收敛速度慢的问题，张博在ACO算法的基础上添加引导因子、循环更新信息素和信息浓度，提出了自适应高斯分布蚁群算法，该算法扩大了无人机的可行搜索空间，能够提供多种路径选择方案，改进后算法的搜索能力强且速度更快。

PSO 算法是1 种生物启发算法，其原理是把搜索空间中的每个粒子都看作1个解。从初始化粒子位置开始，把该位置作为个体最优粒子和全局最优粒子，无人机每经过1个位置就与当前更新的个体最优粒子和全局最优粒子进行比较并更新，最终产生“优秀”粒子群。通常把评估粒子的能力用适应度函数来表示，PSO 算法寻找最优粒子群流程图，如图5 所示。该算法搜索更全面，计算也相对简单，但仍存在易陷入局部最优的问题。

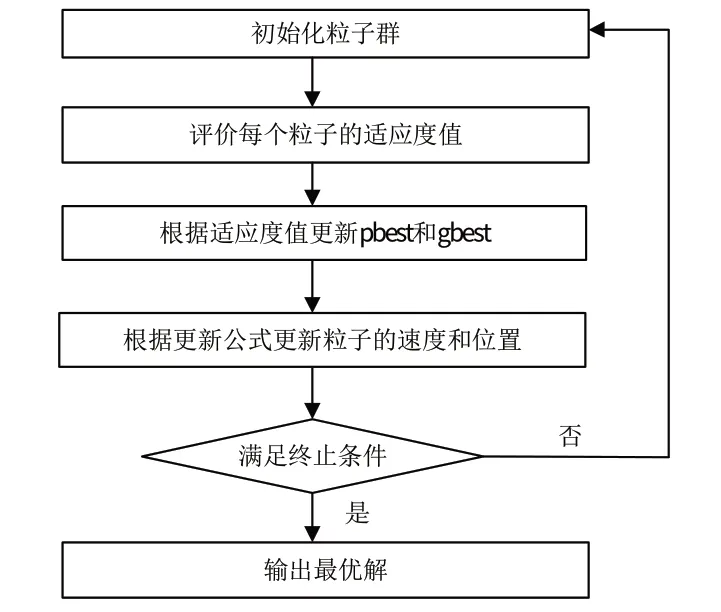
图5 PSO算法流程图Fig.5 Flowchart of PSO algorithm

RobergeV 利用GA 算法和PSO 算法来处理复杂三维环境下的规划问题，为了保证无人机的实时性，通过并行编程“单程序，多数据”来节约运行方案的时间。王磊提出了1 种自适应粒子群优化算法（Adaptive Particle Swarm Optimization，APSO），用来解决固定翼无人机在三维环境空间中的航迹规划问题。仿真结果表明，提出的APSO 算法比PSO 算法更具全局搜索能力和搜索精度。

全局搜索算法是在多无人机执行任务过程中起决定性作用的算法，传统的全局搜索算法存在易陷入局部最优解、计算效率低的问题，需要不断改进这些算法以解决这些问题。在全局取得最优解时，也要考虑局部搜索算法，使得到的航迹在满足条件下尽可能缩短距离。

2 结论

概括来说，从经典算法逐步发展到智能集群算法，无人机航迹规划算法设计取得了长足的发展。但目前的算法仍存在易陷入局部最小值，易早熟停滞和不适用于多模态函数优化的不足。目前，算法的改进或多种算法的结合，如FSSA-SA 算法、改进RRT*算法、自适应粒子群优化算法，更能适用于目前的战场环境。

随着战场环境日益复杂，智能规划算法将是未来无人机规划发展的必然趋势，就目前而言，无人机航迹规划算法仍面临许多的挑战。

1）复杂环境建模困难或模型精度低。实时环境的不确定性和已有数据的不完整性导致建模困难或建立的模型与实际情况差距较大。

2）超强实时性。无人机航迹规划算法大都存在实时性差的问题，超强实时性是未来航迹规划算法亟须解决的问题。

3）计算能力受限。无人机航迹规划算法存在复杂环境算法占内存大、计算效率低的问题，复杂环境对航迹规划算法计算要求较高，计算能力受限导致算法精度不达标。

4）强拒止环境下通信与导航问题。在强拒止环境下，无人机航迹规划常常会因为接收不到准确的环境信息或与“同伴”失联导致任务失败。强拒止环境下的通信与导航是否畅通，将直接影响任务的成功与否。

5）目标识别与智能决策。无人机航迹规划是1个不断识别障碍、规避障碍的过程，高智能等级的目标识别与决策是改进、优化算法的1个关键途径。

无人系统强调机械化、信息化、智能化的“三化”融合，目前，从无人机航迹规划算法可以看出，智能化是未来无人机航迹规划发展的必然趋势。