考虑油膜动态过程的海上溢油应急物资调度优化

张聆晔, 吕 靖, 班 豪, 范瀚文

(大连海事大学 交通运输工程学院,辽宁 大连 116026)

0 引言

随着海上油气勘探的深入和原油运输量的递增，海上发生重大溢油事故的风险逐年上升[1]。一旦出现海上重大溢油必将导致严重的财产损失与难以估计的海洋生态环境破坏。此时，科学高效的物资调度对溢油应急工作的开展具有十分重要的意义。

目前，学者们已对陆上应急物资的调度进行了广泛研究。为解决应急响应过程中存在的物资需求动态变化以及运输网络的不确定性问题，现有研究常用的方法主要有三种，分别为周期规划法[2](Time Period Planning Horizon)、滚动规划法[3](Rolling Planning Horizon)以及随机规划法[4](Stochastic Programming)。

现有研究重在探讨陆上灾害或事故的应急响应，针对海上应急物资调度的研究则较为有限[5]。事实上，由于海陆环境存在较大差异，适用于陆上灾害应急响应的常规方法不足以应对海上溢油应急响应。这些方法的应用是基于假设受灾区域的物资需求以及运输网络的状态在不同的周期或情景内能维持相对稳定，直至下一个周期开始或转换到另一个情景中才对应急系统内关于需求量与运输路径相关的参数进行更新以反映应急响应过程中存在的动态特性。在溢油应急响应过程中，溢油油膜具有扩散和漂移特征，这些动态过程不存在停顿与周期性变更。这样的特点决定了各需求点对应急物资的需求量以及各需求点之间的距离具有时变特征。溢油应急物资调度优化问题势必需要通过构建具有时变特征的动态优化模型进行探讨。

为此，本文在综合考虑受污染区域的时变物资需求、相关运输网络的不确定性以及应急物资调度决策与外部决策环境之间的相互作用关系后，以生态环境损失值最小和应急响应总成本最小为目标构建了一个动态多目标选址-路径规划模型，并基于鲸鱼算法提出了相应的求解方法。

1 问题描述以及假设提出

本文主要以围油栏调度为例探讨海上溢油应急物资的调度问题。由于围油栏的需求量与溢油油膜周长具有正相关关系，溢油油膜扩散时对围油栏的需求量也将相应增加。此外，油膜的漂移运动也将导致应急船的运输网络也具有动态特征。更为重要的是，在进行海上溢油应急物资调度时除了需要考虑油膜动态变化对应急物资调度决策产生的影响外，也需要考虑物资调度本身对油膜变化产生的反作用(如迅速地利用围油栏对溢油进行围控能及时抑制油膜扩散，从而减少需求点对围油栏的需求量)。此时外部决策环境与应急物资调度决策间存在相互作用。

模型构建基于以下假设：

(1)各受污染点的分布情况以及溢油数量可通过地理信息系统(GIS)获得；

(2)油膜扩散速率和漂移速度能维持稳定，应急船也可保持匀速行驶；

(3)在发生物资或运力短缺的情况时可及时获得物资供应方和邻近港口的支援(无等待时长)；

(4)同一个船队中的所有应急船同属于一个应急基地，不存在异地应急船混编现象。

2 模型建立

2.1 相关符号说明

集合:

A：需求点集合，其中a为需求点点引索，a∈A={1,2,…,n}；

B：应急基地集合，其中b为应急基地引索，b∈B={n+1,n+2,…,n+m}；

V：应急系统中所有节点集合，V=A∪B；

R：应急船队集合，r为船队引索，r∈R。

决策变量:

urb：应急船队r是否属于应急基地b，若是urb=1，否则，urb=0，r∈R,b∈B；

yrij：应急船队r是否从节点i出发驶向节点j，若是yrij=1，否则，yrij=0，r∈R,i,j∈V，；

zra：需求点a是否由应急船队r完成物资的运输与投放，若是zra=1，否则，zra=0，r∈R,a∈A，；

kr：应急船队r中所包含的应急船数量，r∈R；

qr：应急船队r所装载的物资总量，r∈R。

2.2 溢油应急物资调度优化模型

考虑到成功的突发事件应急响应应该兼顾效率与成本[6]，溢油应急物资调度的优化目标也据此设定。具体模型构建如下：

目标函数

(1)

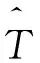
为对生态环境损失进行估值，本文根据佛罗里达公式[7]构建了如下等式：

(2)

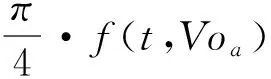
此外，本文主要采用Liu和Leendertes[8]提出的一种溢油扩散模型来反映油膜的变化过程，具体模型如下:

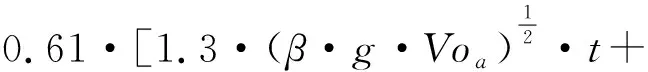
(3)

其中，f(t,Voa)为需求点a处体积为Voa的溢油在t时刻的油膜直径；ρw为海水密度；ρ0为溢油密度，β=1-ρ0/ρw；g为重力加速度；Vo为此处的溢油体积；vw为粘滞系数；t为时间；δ为净表面张力系数。

minZ2=OVOC+SVOC+ORCC+SRCC+TNC+TDC

(4)

式(4)为成本目标函数，表示最小化应急响应成本，整个应急响应过程中产生的成本主要包括如下几个部分：应急基地自有应急船的固定运营成本(OVOC)，临时征用的应急船的固定运营成本(SVOC)，基地自有应急物资的消耗成本(ORCC)，临时增购的应急物资的消耗成本(SRCC)，应急船队在节点间的运输成本(TNC)，应急船队随需求点漂移的运输成本(TDC)。式中，kb应急基地b所配备的应急船总数，b∈B；qb表示应急基地b所配备的应急物资数量，b∈B；vk表示应急船的航速；trij表示应急船队r在节点i和j之间的运输时长，i,j∈V；ct表示应急船的单位距离运输成本；trj表示应急船队r到达节点j的时刻，j∈V;Tri表示应急船队r正要离开节点i的时刻，i∈V；ooc表示应急基地自有应急船的固定运营成本；soc表示向港口临时征调补充的应急；oqc表示应急基地自有物资单位使用成本;sqc表示临时补给物资单位使用成本。

约束条件

(20)

式(5)表示应急船队r到达节点j的时刻；式(6)表示运输船队r在节点间的运输时间，F(Tri)的具体展开内容见式(21)；式(7)、(8)共同表示应急船队r离开不同种类节点的时刻，式中er表示应急船队r的物资投放效率，r∈R；式(9)为基于式(3)所构建的需求量时变函数，当应急物资的种类确定为围油栏时，需求点对围油栏的需求数量等于油膜周长，式中da(t)表示在t时刻需求点a对应急物资的需求量，而gi(t,Voi)表示在t时刻需求点a的需求量增长率；式(10)表示应急船队r的物资投放效率(围油栏布置效率)，式中ek表示应急船的物资投放效率；式(11)表示每个应急船队所配备的运力恰好满足由其负责的所有需求点的应急物资需求总量，式中qk表示应急船的最大载货量；式(12)表示由应急基地i组建的应急船队只能从该应急基地出发；式(13)表示应急船队不会在应急基地间往返；式(14)表示每个节点有应急船队进，就一定有应急船队出，保持流量平衡；式(15)表示每个节点只通过一次应急船队，避免形成未经过应急基地的循环路线；式(16)表示每一个需求点有且仅有一个应急船队对其负责；式(17)表示应急船队途经路径上的节点时存在先后顺序；式(18)～(20)是决策变量的0-1约束。

此外，由于油膜具有漂移特征，当应急船队r完成当前需求点i的运输任务后向下一个需求点航行时，航行距离也因此会处于时变状态。海上各节点间的位置关系可表示如下:

图1中ai、aj为需求点，此时(t=Tri)应急船队r刚好完成对点ai的物资投放并准备前往点aj，应急船队r的航速为vk，点aj的漂移速度为vj，船队从点ai行进到点aj的航行时长为trij，γ为方位夹角，disij(Tri)表示点ai与点aj的当前距离，其中γ、disij(Tri)可通过已知初始条件求得。利用余弦定理构建三边关系等式后，经数学推导可将应急船队的航行时间表示如下:

trij=F(Tri)=[-vj·disij(Tri)·cosγ+disij(Tri)·

(21)

3 算法设计

本文基于鲸鱼算法[9]提出了一种改进的多目标鲸鱼算法(Improved Multi-objective Whale Optimization Algorithm, IMWOA)对构建的优化模型进行求解。

IMWOA的具体计算步骤如下:

Step1初始化鲸鱼种群。

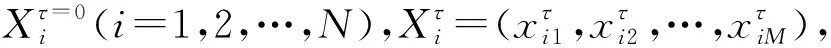
Step2计算鲸鱼个体所在位置的适应度值。

Step3非支配解筛选。

Step4外部档案的更新与维护。

Step5确定领头鲸鱼X*。

现有研究大多对领头鲸鱼进行随机选定[11]，这样做容易导致计算结果局部收敛与早熟。在小生境共享机制中相似个体数越多，则此类个体间的共享度越大，其对应的小生境适应度就越小，反之亦然[12]。鉴于小生境共享机制这一特点，本文决定据此确定外部档案中各个体的小生境适应度值，并在此基础上通过轮盘赌筛选作为领头鲸鱼X*的个体，从而确保解的多样性，以避免局部收敛和早熟情况的出现。

Step6更新种群中鲸鱼个体的位置。

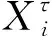
A=2·a·r-a

(22)

(23)

式中，a的取值介于区间[0,2]且随迭代次数τ的递增而线性递减；r为介于区间[0,1]的均匀分布随机数。具体更新方式见文献[9]。

在标准WOA中，全局搜索和局部搜索之间的取舍主要由收敛因子A决定。随着a的线性递减，A也随之递减，易导致领头鲸鱼陷入局部最优。为此，本文采用一种先缓慢递减后急剧递增的函数(见式(24))代替标准WOA中关于收敛参数a的线性递减函数(见式(23))。

(24)

Step7重复Step 2～4，并获得更新后的外部存档，随后转到Step 8，判断是否终止迭代计算。

Step8判断终止条件。若满足最大迭代次数(τ=T)，则直接输出计算结果；否则，τ←τ+1，转到Step 5，继续搜索。

4 仿真案例分析

4.1 背景及数据

从事故发生到对事故海域完成溢油监测并采取实际的应急行动，时间间隔有7小时。此时，海面已出现数量众多且分散的油膜区域，其中共有20处油膜较厚的需求点急需围油栏对其进行围控。这些油膜在两股不同海流作用下主要出现两种不同的漂移方向与速度，部分油膜以1.8kn速度向南偏东32°方向漂移，另一部分油膜以1.2kn速度向北偏西28°方向漂移，油膜数量、位置及其漂移速度等相关信息见图2。事故海域近邻的应急基地共有3处，分别是大连基地、烟台基地以及威海基地，各应急基地的物资库存、船舶配备、物资消耗成本等与应急物资相关的信息见表1。应急船的航速、运力以及使用成本等信息见表2。

图2 需求点分布情况

表1 应急基地物资储备情况

表2 应急船性能及其使用成本

4.2 算法比较

为求解模型，本文利用MATLAB软件对IMWOA算法进行程序编写，并将IMWOA算法相关参数经多次试验后设置如下：种群规模N=50，最大迭代次数T=300，共享距离σshare=2.8。由于NSGA-II被广泛应用于多目标问题求解且该算法的有效性也获得了研究领域的普遍认可，故选择其作为对比算法以检验利用IMWOA所求得的Pareto解集的质量。为保证分析结果对比的有效性，两种算法的参数尽量一致，关于NSGA-II的相关参数设置如下：种群规模为50，最大迭代次数为300，交叉概率为0.8，变异概率为0.05。为求得精确Pareto前沿的近似解，两种算法各运行10次并取整合后的结果作为计算结果，如图3所示。

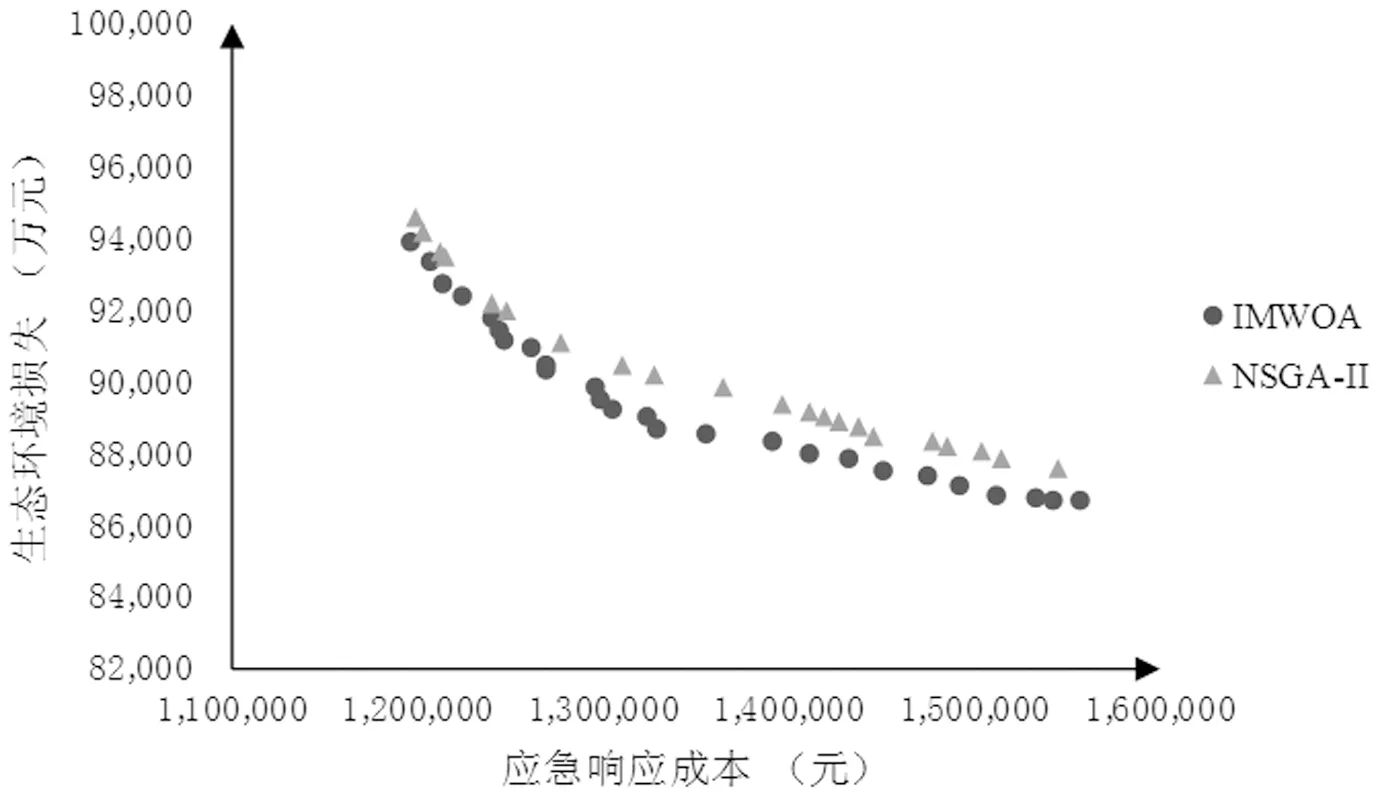
图3 IMWOA和NSGA-II的Pareto解分布

经对比可发现，NSGA-II求得的Pareto解均受IMWOA求得的解的支配，IMWOA在精确度方面明显优于NSGA-II。就多样性而言，IMWOA求得的解相较于NSGA-II而言数量更多，分布更为均匀。而NSGA-II求得的解则明显分布不均，鲁棒性较弱，主要是由于算法运行到中后期时难以逃脱局部最优而陷于局部区域搜索。由此可见，IMWOA具有更高的求解精度与更强的搜索能力，不仅能有效避免陷入局部最优，同时还保证了解的多样性，使Pareto解集分布更加广泛，能够为决策者提供更优质、更充足的应急物资调度决策参考。

4.3 计算结果

利用IMWOA求出Pareto解集后根据理想解选取模型[4]求得评分最高的解的得分为0.6268，其调度方案如表3所示。在表3中，每个应急船队运输应急物资的路径由其抵达的节点顺序表示。以应急船队1为例，其运输路径为21- 6- 8-13-3-21，表示该船队从其所属的大连基地(节点21)出发，依次向需求点6、8、13以及3运输应急物资，最终回到大连基地(节点21)，完成其应急物资运输任务。每个船队的配船情况以及应急物资(围油栏)的分配情况也可由表3获知。此时生态环境损失为8.902×108元，应急响应成本为1.323×106元。

表3 动态环境下的理想调度方案

5 结论

本文通过对油膜动态过程进行分析，构建了动态多目标选址-路径规划模型以解决溢油应急物资调度优化问题。然后根据模型特点，设计了IMWOA算法对其进行求解。仿真案例分析结果表明，该动态模型能良好地反映油膜运动与应急决策之间的相互作用关系；在算法方面，与NSGA-II相比，IMWOA搜索能力更强，能保障模型的求解效率。

在进一步研究中，将充分考虑不同应急物资的使用条件与储运特点以探讨多种物资协同调度情景下的溢油应急物资调度问题。