移动机器人履行系统配置优化研究
——基于闭排队网络理论
2022-05-14冯爱兰马立坤孔继利
冯爱兰, 杨 腾, 马立坤, 孔继利
(北京科技大学 机械工程学院,北京 100083; 2.北京科技大学 天津学院 机械工程系,天津 301830; 3.北京邮电大学 现代邮政学院,北京 100876)
0 引言
移动机器人履行系统(RMFS,Robotic Mobile Fulfillment Systems)是一种“货到人”的拣选模式,商品被存储在可移动的货架中,通过智能仓储移动机器人搬运可移动货架,实现货架在存储位置和拣选台之间快速移动,员工在拣选台完成拣选活动,常见如Kiva系统。移动机器人履行系统具有移动性、模块化、灵活性等特点,有效解决了B2C企业订单数量多、单笔订单小、品类多[1]、时效敏感等问题,在亚马逊、京东、天猫超市等电商企业得到迅速应用。
RMFS的应用带来了拣选模式的颠覆,如何通过模式研究、配置优化、策略提出实现系统履行效率优化成为学者关注的问题。周晓光[2]、John Tersko等[3]对RMFS模式进行了详细介绍,分析了RMFS的特点及适用性等问题。李晓杰[4]考虑货架内商品相关性对系统履行绩效的影响,提出基于商品相似度系数的聚类方法,通过优化储位有效减少货架调度次数。Nils Boysen[5]、Xiang等[6]关注拣选前的订单处理行为,通过订单分批、订单排序、货架调度等问题的算法优化实现货架调度次数最少。在拣选过程中,多机器人的路径规划[7~9]和调度策略[10~13]问题是研究的热点。同时,学者常通过系统绩效对不同策略和设施布局进行评估,常见有仿真建模、排队网络建模等方法,Jin等[14]利用仿真研究了在不同的仓库布局和不同机器人数量的场景中,订单指派规则对系统履行绩效的影响。Lamballais T[15]用半开排队网络讨论了多种储位规则、订单指派规则、补货规则和货架调度规则对系统履行绩效的影响。Zou等[16]通过建立半开的排队网络模型计算不同充电方式在相同吞吐量下的运行时间,探究无线充电、插电充电、更换电池三种充电方式对RMFS履行绩效的影响。黄惠春等[17]建立闭排队网络模型对医药配送中心进行研究,通过数据分析解决系统的拥堵问题。与仿真极尽还原真实环境相比,排队网络模型忽略系统的次要因素和环境的影响,是对系统分析和关键问题的抽象表示,具有模型容易修改、应用灵活、求解迅速的优点。
考虑到RMFS中,货架、拣选台的数量和位置、机器人的数量等因素都可以在短时间内实现迅速调整,要充分发挥RMFS模块化、机动灵活等优势,就必须将RMFS的布局问题看成随着业务量变化不断改变的动态决策问题。本文针对RMFS任务履行过程的特点,从货架调度任务角度分析建立闭排队网络模型,采用近似平均值分析算法求解,进而评估拣选台、机器人利用率和调度任务履行能力,用仿真实验验证其结果可靠性,并对系统设施配置进行讨论和优化。
1 移动机器人履行系统分析
1.1 系统组成和参数设置
RMFS由可移动货架、智能仓储移动机器人、拣选台组成。货架在仓库中按一定规则排布,通常以矩阵块的形式存在。货架之间存在横纵巷道,货架通过巷道实现在存储位置和拣选台之间的移动。单向巷道的设计在一定程度上减少了空间面积的占用,在RMFS场景中应用较多。智能仓储移动机器人是系统的关键组成部分,货架的搬运需要借助机器人实现,仓库的拣货和补货活动都需要机器人的参与。空载的机器人可以在货架下自由的穿行,驮载货架的机器人则需要按照巷道规定的方向在巷道内移动。拣选台一般设置在仓库的侧边,拣选员只需按照系统的指示,拣选当前货架内的指定商品或将指定商品放入货架中。典型布局如图1所示。

图1 移动机器人履行系统
系统布局参数设置如表1所示。

表1 布局参数描述
1.2 系统分析和数学表达
仓库的布局、设备设施的数量、订单履行的流程和策略都会对系统履行绩效产生影响。在系统中,储区矩阵块的规模为5×2,当纵向巷道和横向巷道的数量确定时,可以得到储区可容纳的货架数量Cw=2×5×(na+1)(nb+1),仓库的长宽可以用公式(1)求得。
(1)
货架位置用(Xai,Xbi,Yai,Ybi)表示,其中Xai表示沿X轴正方向,货架位于第几个矩阵块,Xai=1,2,…,na+1;Xbi表示货架位于矩阵块中的第几个货架,Xbi=1,2,…,5;Yai表示沿Y轴正方向,货架位于第几个矩阵块,Yai=1,2,…,nb+1;Ybi表示货架位于矩阵块中的第几个货架,Ybi=1,2。如图1中所示的货架坐标可用公式(2)表示:
(2)
拣选台位于仓库的侧边,当同侧有多个拣选台时,拣选台均匀分布。用(Xst,Yst)表示拣选台的坐标,NE,NW,NS,NN分别表示东、西、南、北四侧拣选台的数量,各个方向拣选台的坐标如下:
(3)
(4)
2 闭排队网络分析与建模
2.1 RMFS任务履行过程
在RMFS履行过程中,原始订单经过处理形成拣选订单批次,并确定订单履行顺序及相应的货架调度任务。货架调度任务指派给智能仓储移动机器人,由机器人实现货架在拣选台和存放位置之间的搬运,拣选台按照系统指派的任务完成订单拣选或补货工作。RMFS履行过程即货架调度任务的完成过程,一次货架调度任务主要可以分为以下过程:
(1)装载货架:机器人获得货架调度指令,从驻留点向目标货架所在位置移动。该过程中,机器人空载行驶,可以自由地从货架底部穿过,机器人的运行路径为驻留点到目标货架位置之间的最短路径,长度为两地之间的曼哈顿距离。到达目标货架下方后,机器人将目标货架抬起,机器人的状态变为负载状态。
(2)搬运货架:机器人将货架从目标货架所在位置搬运至拣选台。驮载着货架的机器人只能在预先规划的单向通道中行驶,行驶距离为遵循通道行驶方向的最短路径。
(3)拣选货架:机器人经过排队到达拣选台,拣选员工按照系统指示放入或拣出商品,完成工作后向机器人发送完成信号。
(4)卸载货架:机器人按照货架调度指令,将货架驮载回储区的空闲位置,放下货架并在该位置驻留待命。
2.2 RMFS闭排队网络建模
闭排队网络是排队网络的一种,是一个完全封闭的系统,系统中的服务台、顾客数量都是恒定的,顾客在不同的节点之间转移,没有顾客到达或离开系统。
机器人在整个任务履行过程中,不仅有空载、负载、行驶、驻留的状态变化,还存在装、卸货架的行为转换。因此,可以根据机器人状态、行为的不同,将RMFS看成一个闭排队网络,机器人作为顾客需要接受装载货架、运输货架、卸载货架的服务。为描述机器人驮载货架到拣选台的活动,需要虚设一个“运输”服务节点。因为不存在两个机器人接受同一个货架调度任务的情况,所以装、卸载货架的服务台节点设置成无限服务台类型。另外,由于仓库面积足够大,足够容纳所有机器人运输货架,运输服务节点同样设置成无限服务台节点。
整个任务履行过程中,智能仓储移动机器人始终不会离开系统,数量保持一定,机器人的速度一定,拣选人员工作简单,操作过程中意外事件概率较低,因此排队网络可以达到稳态。各个节点任务结束后,转移方向互不干扰,各节点之间是相互独立的。根据上述条件,将智能仓储移动机器人视为顾客,货架调度的四个过程视为四个服务节点,建立闭排队网络模型如图2所示。

图2 RMFS闭排队网络模型
在订单拣选过程中,由于货架在仓库中随机摆放,货架装载位置或货架卸载位置在任一货位的概率是相等的,即:
(5)
3 闭排队网络求解
3.1 近似平均值分析算法
在RMFS订单拣选过程中,服务节点的服务时间无法用传统的概率分布描述,属于非马尔可夫排队网络,因此乘积形式求解排队网络的方式已经不再适用。考虑到模型各个节点的平均服务时间及标准差等是可求得的,选择采用近似平均值分析算法求解,其参数的定义见表2。

表2 近似平均值分析算法参数设置
节点i的相对到达率λi可以通过公式(6)求得,其中pij表示节点i向节点j转移的概率。在本文中,由于转移方向一定,pij均取1/H。
(6)
详细求解过程如下:

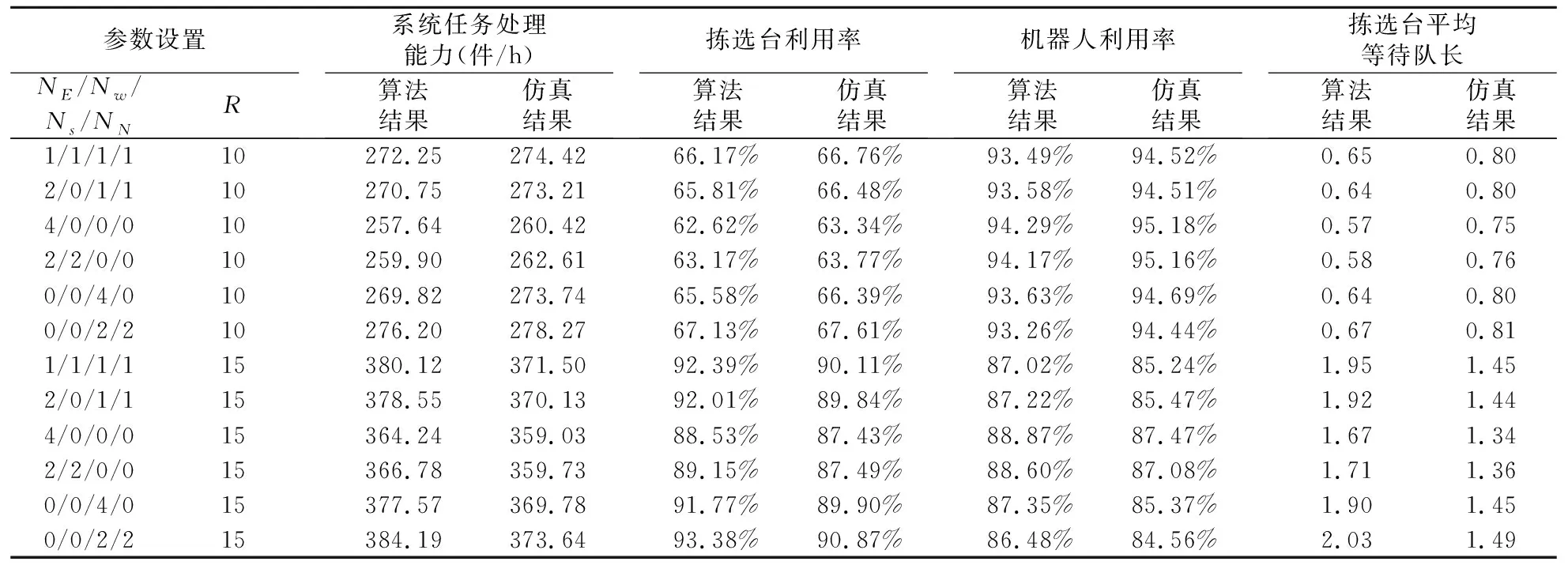
1:Initialization2:Qi(0)=0,Li(0)=0,i=1,2,…,H %数据始化3:Preprocessing4:for i=1:Hdo5:Remi=Ei2(1+(σiEi)2) %节点i的残余服务时间6:end for7:for i=1:Hdo8:for i=1:Rdo9:Wi(r)=Qi(r-1)Remisi+Li(r-1)EiSi %节点i中机器人的平均等待时间10:Wpi(r)=Wi(r)+Ei %节点i中机器人的平均逗留时间11:end for12:for i=1:R do13:HTi(r)=r×λi∑Hi=1λi×Wpi(r) %节点i单位时间内任务的平均到达量14:Li(r)=THi(r)·Wi(r) %节点i的平均队长15:ρi(r)=THi(r)·Ei/Si %节点i的服务利用率16:if 由此可以计算系统评价的相关指标,系统的任务处理能力为(TH3(R)×3600)件/小时,机器人的利用率为(1-L3(R)/R),拣选台的利用率为ρ3(R)。 近似平均值分析算法是利用节点平均服务时间和标准差评估系统的方法。在RMFS中,受通道方向和最短行走距离的限制,机器人的行驶轨迹是可得的。在机器人行走速度一定的条件下,各个服务节点的平均服务时间和标准差也是可求的。另外,为方便计算,简化问题的复杂度,将货架宽度近似于货架储位宽度,同时假设货架能在通道中顺利行驶,不产生拥堵碰撞。 ②搬运货架过程中,驮载着目标货架的机器人只能在预先规划的单向通道中行驶,行驶距离为遵循通道行驶方向的最短路径。 当拣选台(Xst,Yst)位于仓库的南或北侧时,货架到拣选台的平均服务时间是相同的。以拣选台位于南侧为例,货架到拣选台的行驶过程分为四个阶段:(1)机器人将货架驮载到临近的巷道;(2)到达最近的下行巷道;(3)行驶到仓库最底部;(4)行驶至拣选台。距离Lp2s是以上四个阶段的距离之和。 当拣选台位于仓库的东侧或西侧时,货架到拣选台的平均服务时间是相同的。以拣选台位于西侧为例,货架到拣选台的行驶过程分为五个阶段:(1)机器人将货架驮载到临近的巷道;(2)到达最近的巷道;(3)行驶到朝向拣选台的最近横向巷道;(4)沿横向巷道行驶至最西侧;(5)行驶至拣选台。距离Lp2s是以上五个阶段的距离之和。 以图1所示的仓库布局为基本的实验场景,具体的实验参数值如表3所示。将建立的闭排队网络模型和近似平均值分析算法应用到算例中,为验证结果的可靠性,将算法结果与仿真实验结果对比。在此基础上,对整个系统的设施配置进行分析和优化。 表3 实验参数值设置 由于节点1、2、4都为无限服务台节点,机器人到达该节点时能立即得到服务,不会产生等待时间。可以推测当机器人数量足够多时,节点3即拣选台的服务能力是整个系统的瓶颈。因此,拣选台的数量和位置是影响系统履行能力的重要因素。考虑到拣选台位于南侧NS和北侧NN(东侧NE和西侧NW)的对称位置时,其各个节点的平均服务时间相同,本文仅讨论对称拣选台位置中的一侧。参考文献[15]设置,假设拣选台的拣选时间服从U[20,50]的均匀分布,实验对10/15台机器人和4个拣选台的系统场景进行实验探究。仿真实验采用Matlab的离散仿真计算方法,对N=50000条货架调度任务的履行过程进行模拟,随机产生初始货架分布位置、任务调度货架及相应的目标拣选台,由R个机器人依次完成货架调度任务,具体计算流程如图3所示。最终,系统的任务处理能力TH(R)=N/Tf,机器人的利用率ρR=Σ(Tt2p+Tp2s+Ts+Ts2p)/(R×Tf),拣选台利用率ρs=ΣTs/(H×Tf),拣选台平均等待队长通过统计不同时间段拣选台前等待的机器人数量求得。 将仿真计算得到的平均数据指标与算法结果进行对比,结果如表4所示。 图3 仿真计算流程图 表4 服务台位置对系统绩效的影响 从表4结果可以看出,拣选台位置会对系统履行绩效产生一定影响。拣选台位于南、北两侧的系统履行绩效要优于拣选台位于东西两侧的场景。这是因为当拣选台位于南北两侧时,机器人完成一次调度任务所需要行走的平均距离小于东西两侧的场景。同时,拣选台利用率的提高伴随着机器人利用率的降低,原因是拣选台平均等待队长增长,机器人在排队等待中消耗了更多的时间。其次,拣选台分散于两侧与集中于一侧相比,系统的履行绩效有所提升。因此在考虑仓库拣选台布置时,应优先将拣选台布置在仓库较长的侧边,且将多个拣选台分布在两侧而非集中于一侧。 节点3是整个系统的瓶颈,拣选台的利用率决定了系统的履行效率。同时,机器人是整个系统履行过程的重要参与者,机器人数量太少会降低系统履行效率,机器人数量过多又会增加不必要的投入和能耗。合理的机器人配置应该在保证系统绩效的前提下数量最少。 以研究所得的拣选台最优位置0/0/2/2为基本场景,探究机器人数量配置问题。由图4可知,当拣选台数量一定时,随着拣选台利用率的增加,系统任务履行能力在逐渐增强,同时伴随着机器人利用率的降低。结合实际很容易理解这种变化的合理性:拣选台利用率增加伴随着平均队长的增加,同时意味着等待拣选的机器人越多,机器人在等待中浪费的时间越长,利用率越低。当机器人数量为17时,拣选台的利用率接近100%,但考虑到实际应用场景中,各种设备机械都有最佳利用率,100%的利用率并不利于设备的保养。通过综合考虑,当机器人数量为13台或14台时,机器人和拣选台的利用率均在85%以上,综合利用率较高。 图4 机器人数量优化配置 综上,拣选台数量为4台,均匀布置于南、北两侧时,机器人可选择投放数量为13或14,控制拣选台利用率在85%以上,系统履行效率较高。 本文将RMFS中货架调度任务的履行过程拆分成装载货架、搬运货架、拣选货架、卸载货架四个过程,进而转化成四个服务节点建立闭排队网络模型,采用近似平均值分析算法求解。通过仿真实验验证了算法的有效性,并通过计算结果对系统设施配置问题进行分析,实现系统履行绩效的评估。由分析可知,拣选台均匀分布于仓库较长的两侧能够提高系统履行效率,且存在机器人较优投放数量使系统履行效率较高。研究从货架调度任务角度对系统进行分析,不考虑订单波动和订单拣选方式对系统履行绩效的影响,对系统初始规划具有重要意义。 采用排队网络模型分析忽略了多机器人运行场景中可能出现的拥堵、避让等状况。另外,当前的研究关注于典型布局中拣选台位置及机器人数量对系统履行绩效的影响,忽略了机器人任务指派方法、货架储位指派等因素,相关问题可以作为进一步的研究方向。3.2 服务节点的平均服务时间和标准差
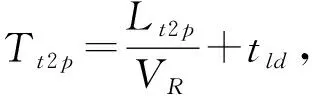


4 实验分析



5 结论
