基于DEA交叉评价的模糊有效性度量方法

斯 琴, 马占新

(1.内蒙古大学 经济管理学院,内蒙古 呼和浩特 010021; 2.内蒙古财经大学 统计与数学学院,内蒙古 呼和浩特 010070)

0 引言

对于模糊指标与效率指标同时存在的多属性模糊事件评价问题, 由于指标的多属性,通常难以根据一些数学方法直接对其进行分析。模糊综合评判方法可以较好地应用于带有不确定性等特性的评价研究, 而数据包络分析方法(DEA)[1～4]是效率分析研究中一种重要的工具, 该方法利用评价单元的投入产出数据得出效率值, 对评价单元进行分析。因此,结合这两种分析方法有助于综合评价问题的研究。

1992年Sengupta[5,6]首次提出模糊数据包络分析方法后, 相关研究就受到广泛关注。如1998年Triantis和Girod[7]用传统的数据包络分析框架, 结合模糊参数化的概念, 提出了一种三阶段方法来评价模糊环境中的技术效率。2000年Kao和Liu[8]通过应用α截集方法将模糊DEA模型转换为传统DEA模型。2004年彭熠[9]提出处理含有模糊数据的多目标规划DEA模型等。上述研究是对输入输出指标为模糊数的评价对象的效率分析问题进行探讨, 并没有对模糊综合评判方法本身进行完善[10]。2001年马占新等[11]基于模糊综合评判基础给出了一种评价模型, 该方法加强了评价分析的客观性,为改进提供了相应策略。2010年柳顺等[12]利用数据包络分析方法和模糊综合评价方法分别对效率指标和模糊指标进行评价, 再采用模糊评判方法对所有指标再评价, 建立了客观性较强的组合模型[13]。2012年郭庆娥等[13,14]根据DEA交叉评价的思想, 建立了基于交叉评价的模糊综合评价方法。文献[12～14]将DEA效率评价和模糊综合评价有机结合在一起, 并在具有效率指标和模糊指标的混合型模糊对象的综合评价中得到很好应用, 但这些方法无法进一步提供指标的评价结果的改进策略。

为此,本文将文献[10]中的方法拓展到针对模糊指标与效率指标同时存在的多属性模糊事件评价问题。首先对效率指标采用DEA交叉效率评价方法进行评价, 将得到的交叉效率值进行模糊化处理后, 综合所有指标的评价信息构建模糊评价可能集；然后给出模糊有效性的概念及相应评价模型。所提出的方法不仅能找出处于劣势的评价对象与其有效状态的差距, 还可以基于模糊可能集的信息为决策者提供各因素评价改进的信息及方向。

1 模糊事件评价可能集的构造

1.1 问题的描述

假设在对某n个模糊事件进行评价,每个模糊事件的指标如图1所示,其中B中的指标为效率指标(o1,o2,…,oL),每个效率指标可以分解出由精确数构成的投入产出指标,如第k个效率指标的输入输出指标为(xk,yk);Y中的指标为模糊指标。

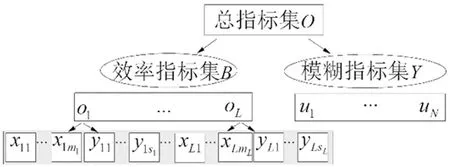
图1 模糊事件指标分解图

例如对于n个实验室的综合评价问题, 实验室的评价指标集为U={人力财力, 运行管理, 实验科研, 资源共享}[12]={o1,u1,u2,u3},评价集为V={优,良,差}={v0,v1,v2}。其中,

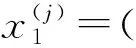
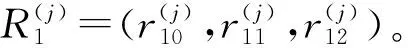
1.2 效率指标的评价处理

本文主要是应用模糊综合评价方法的相关信息, 来构建模糊事件的模糊评价可能集, 进而给出模糊有效性的定义, 以及模糊事件无效原因的分析方法。其中, 模糊事件可能集的构建基础是模糊综合评价矩阵, 但由于效率值为精确数, 不具有模糊综合评价所需的隶属函数。因此下面首先根据文献[13]采用DEA交叉效率方法对模糊事件的效率指标进行评价,然后对效率指标进行模糊化处理, 从而实现模糊事件可能集的构建。

下面采用DEA交叉效率分析方法对各模糊对象的第l个效率指标ol进行评价。被评价模糊对象j在效率指标ol下对应的线性规划为

1.3 模糊事件评价可能集

下面基于本文中评价对象的效率指标与模糊指标的模糊隶属度, 来构建该类模糊事件的评价可能集。应用文献[10]提出的模糊事件评价可能集的构造原理可以得出以下结论。

假设n个模糊事件属于同一类事件集S,评价集为V={v0,v1,…,vt-1},则对任意模糊事件j(∈S)有,

根据文献[10]中的构造原则, 可以给出如下模糊事件评价可能集。

上式进一步的说明,对于任意的模糊对象j(∈S)而言,任何P∈SL也都是被评价对象j可能得到的指标状态。

2 模糊事件的综合评价与投影分析

2.1 模糊事件的有效性与综合评价

定义1对于模糊对象j0,若不存在P∈SL,使得f(P)≥f(Pj0)且至少有一个不等式严格成立, 则称模糊对象j0为F-DEA有效。

定义1表明,从现有可获得的经验数据分析,若同类型对象中不存在某个对象的指标评价值比模糊对象j0更好,即达到pareto有效,则认为模糊对象j0为F-DEA有效。

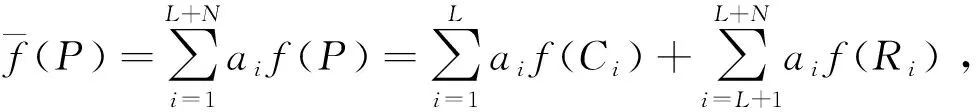
定义2对于模糊对象j0,若P(j0)为线性规划(FM)的最优解, 则称模糊对象j0为FZ-DEA有效。

定义2表明,从现有的经验数据进行分析, 若同类型对象中不存在某个对象的总体评价值比模糊对象j0的更好, 则认为被评价对象j0为FZ-DEA有效。

根据文献[10]有如下定理成立。

上述定理中f(SL)表示基于现有可获得的经验数据来分析, 评价对象指标评价值可能存在的状态。

2.2 模糊有效性度量及投影分析

根据文献[10]可以给出如下数学模型(FD),并有以下定理成立。

其中ε为非阿基米德无穷小量。

根据文献[10]有如下定理成立。

因此,根据所计算出的投影值可以对某个模糊对象进行分析,找出综合测评的无效原因,或是某模糊对象组的综合测评较差的原因。下面根据文献[10]可以给出相应的测度方法。

2.3 无效原因分析与改进策略

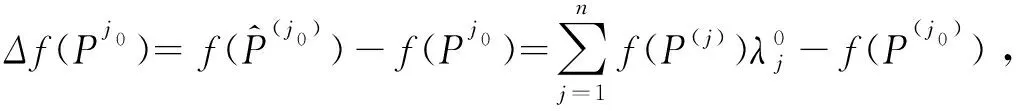
结合上述各模糊对象的相关信息,针对某个小组的不足原因进行分析时, 给出以下测度方法。

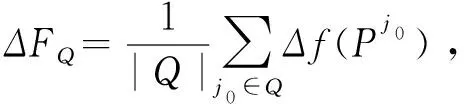
(2)为向决策者提供有针对性的改进信息, 结合相应的信息分别给出模糊对象个体和群组改进的方法。

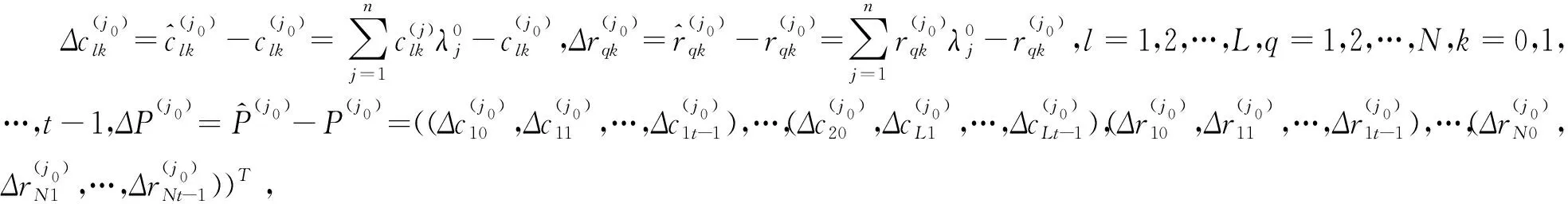
根据个体改进策略, 下面给出分析某个群组整体的改进策略的测度方法。

3 算例分析

为了进一步说明本文方法的改进效果, 以下采用文献[12]中8个实验室的有关数据进行比较分析。

在评价过程中,实验室的评价因素集为U={人力财力,运行管理,实验科研,资源共享}={o1,u1,u2,u3},其中,人力财力是由人数,资金投入,委托检验收入组成的效率指标,运行管理,实验科研,资源共享为模糊指标。设决策者决定各因素的权重集为A={a0,a1,a2,a3}={0.375,0.250,0.250,0.125},评价集为V={v0,v1,v2}={优,良,差}={1,0.75,0.5},文献[12,13]给出的评价集与隶属函数的对应关系、指标体系如表1所示。

表1 各实验室统计数据

3.1 实验室评估的模糊综合评判

(1)按照DEA交叉评价的步骤计算各实验室的人力财力的效率值,其中人数、资金投入为输入指标,委托检验收入为输出指标,再将效率值模糊化为隶属度,结果如表2所示(数据来源文献[13])。

表2 效率指标的交叉效率值及评价的隶属函数

(2)结合效率指标及模糊指标的隶属度, 应用传统的模糊综合评判方法对各实验室进行评价分析, 运用加权平均法进行计算, 其值如表3所示。

表3 实验室综合评价结果

从表3的计算结果可以看出,综合评价值最高的是实验室8,评价值为0.875,表示在所有实验室中实验室8综合表现最好;评价值最低的是实验室4,评价值为0.687,说明其在所有实验室中综合表现相对最差。其中实验室1、2、3、5、6、8的评价值大于0.7,评价结果介于良与优之间;实验室4、7的评价值小于0.7,但大于0.5,评价结果介于差与良之间。

3.2 实验室的无效原因分析

下面应用本文给出的方法可作如下分析。首先对综合评价较差的两个实验室进行分析,然后对综合评价值低于0.75的实验室找出总体原因。

(1)实验室个体的无效原因分析

下面根据Δf(Pj0)的计算公式对评价结果较差的实验室4、实验室7进行计算,结果如图2所示。其中,Δf(p(4))=(0.034,0.123,0.098,0.048),Δf(p(2))=(0.048,0.071,0.096,0.096)。

图2 实验室的无效原因分析

结合表3和图2可以得出:实验室4的评价值为0.687, 该实验室的所有指标中资料共享评价较好,无效值较低；运行管理和实验管理的评价值还需要较大的提升。实验室7的评价值为0.693,该实验室的所有指标中运行管理、实验管理和资源共享则都需要较大的提高。

(2)实验室群体的无效原因分析

根据ΔFQ的计算公式对综合评价值低于0.75的实验室进行计算得出,ΔFQ=(0.038,0.081,0.089,0.064),可以看出综合评价值低于0.75的实验室的各指标均存在一定差距,其中实验管理、运行管理的改进空间较大。

3.3 实验室的改进分析

根据各实验室所找出的不足,应用本文的方法给出相应的改进分析。

(1)实验室个体的改进策略分析

下面根据的计算公式对实验室4、实验室7的数据进行计算,其结果如表4所示。

表4 基于模型(FD)的个体改进策略信息

从上面的分析看,由于实验室4人数较多,资金投入较多,但委托检验收入不高。结合已获得的经验数据和表4的相应结果给出实验室4的如下改进:

在人力财力方面,将差评中的0.137转化为良评,使人力财力方面评价结果有所提高。在运行管理方面, 消除差评,并将优评提高0.2,良评提高0.093,进而大幅提高优评的结果。在实验科研方面,努力消除差评,将优评提高0.2,使实验科研的优评提高。在资源共享方面,还需要继续努力消除差评,将优评提高0.1,使资源共享整体水平有所提高。

由于实验室7人数居中,资金投入较少,委托检验收入不高,基于表4的计算结果,实验室7的努力目标是:

在人力财力方面,将差评中0.191转化为良评,进而大幅提高评价结果。在运行管理方面,消除差评,将优评提高0.1,良评提高0.086,进而大幅提高优评的结果。在实验科研方面,积极消除差评,将优评提高0.2,使实验科研的评价结果提高。在资源共享方面,做出更多的努力消除差评,将优评提高0.1,良评提高0.186,资源共享整体水平有所提高。

(2)实验室群组的改进分析

结合各实验室的信息,根据ΔPQ的公式进行计算,可得出综合评价值低于0.75的实验室组的指标值P(j)(∈Q)的平均值PQ及其可行有效调控量ΔPQ如表5所示。

表5 基于模型(FD)的群组改进信息

从表5可以看出,对评价结果低于0.75的实验室组:

在人力财力方面,将差评减少0.151,良评提高0.151,进而提高评价结果。在运行管理方面,积极消除差评,使优评值再提高0.167。在实验科研方面,努力消除差评,将优评提高0.2,提高评价结果。

上述分析给出了具有参考性的改进方向,实验室负责人根据相应分析可以对落后实验室进行调整,从而得到全面的发展。

4 结论

本文针对模糊指标与效率指标同时存在的多属性模糊事件评价问题,结合所有指标的模糊隶属度构建了相应的评价可能集,并给出模糊有效性的定义,及构造了相应的评价模型。本文算例表明,所提出的方法不仅从各效率指标和模糊指标的模糊综合评价值中找出了处于劣势的评价对象与其有效状态的差距,还可以基于模糊可能集的信息为决策者提供了各因素评价改进的详细信息及方向。