热力学计算模拟对初始月幔结构的约束*

鞠东阳 庞润连 李瑞 杜蔚, 3

1. 中国科学院地球化学研究所，矿床地球化学国家重点实验室，贵阳 550081 2. 中国科学院大学，北京 100049 3. 中国科学院比较行星学卓越创新中心，合肥 230026

自从在Apollo 11任务返回的月海玄武岩样品中发现了斜长岩角砾，很多学者提出月球早期存在岩浆洋，且月壳是由岩浆洋结晶分异的密度较低的斜长石上浮而形成(Smithetal., 1970; Woodetal., 1970)。对阿波罗计划返回的月球样品的详细研究发现月球高地斜长岩存在Eu正异常特征，且相应的月海玄武岩具有Eu负异常特征(Ryder, 1982)，同时月球样品具有较为集中的Hf-W模式年龄(Thiemensetal., 2019)，这些都为月球形成后经历过大规模的岩浆洋结晶分异过程提供了有力的证据。另一方面，月球起源的“大碰撞”模型认为原始地球与一个类似火星大小的星体发生碰撞而形成了月球(Canup, 2012)，这一碰撞事件为月球岩浆洋的形成提供了足够的能量(Elkins-Tanton, 2012)。

月球岩浆洋的形成是月球演化的起点，月球内部的物质组成和初始结构都与岩浆洋的结晶演化过程直接相关。月球岩浆洋结晶分异所形成的初始月壳和月幔决定了早期月球内部的组成、密度和结构，控制着月球后续的演化过程，是整个月球演化过程中最基础的部分。早期的岩浆洋结晶模型认为：富镁的橄榄石最先结晶，之后是斜方辉石，岩浆洋后期结晶的斜长石由于密度较小而上浮形成原始月壳；随着分离结晶的进行，残余岩浆越来越富铁，结晶的矿物形成致密的富钛铁矿层；最终残留的月球岩浆洋富含钾(K)、稀土元素(rare earth elements, REE)、磷(P)和其他不相容元素，与克里普(KREEP)储库的形成密切相关(Warren, 2005)。密度较大的岩浆洋晚期结晶的钛铁矿等富铁物质可能由于重力不稳定而发生翻转，导致早期和晚期岩浆洋结晶堆积物发生不同程度的混合和部分熔融，形成的熔体上升至月球浅部甚至表壳，这一过程能够解释月球表面某些特征单元，例如镁质岩套等的成因(Elkins-Tantonetal., 2002)。但是，这种单一阶段的岩浆洋演化模型在解释复杂的月球样品的一些特征时遇到了困难，例如镁质斜长岩中的镁铁质硅酸盐矿物的Mg#(MgO/(MgO+FeO)的摩尔比)存在差异，暗示其并非来自单一源区(Xuetal., 2020)。月球样品中稀土元素含量存在差异以及斜长岩较大的年龄分布范围(4.29～4.55Ga)等，指出其并非来自同一阶段的结晶分异(Grossetal., 2014; Russelletal., 2014; Borgetal., 2020)。对这些问题进行解释需要重新考虑月球岩浆洋演化过程的细节，特别要关注形成的初始月壳的成分和厚度以及月幔深部的物质组成和结构。

月球岩浆洋模型中的几个基本假设，岩浆洋的初始物质组成、初始深度以及岩浆洋存续的时间长度等仍存在较大争议(Warren, 2005; Mauriceetal., 2020)，而这些参数均会影响到岩浆洋的结晶过程以及月球的初始内部结构。关于月球岩浆洋初始物质组成的争论主要是MgO的相对含量(本文以Mg#表示)和难熔元素的含量(Warren, 2005)。目前能够代表月球岩浆洋初始物质组分的两类端元模型分别为泰勒全月球模型(Taylor Whole Moon, TWM)和月球原始上地幔模型(Lunar Primitive Upper Mantle model, LPUM)(Longhi, 2006; Taylor, 1982)。这两个成分模型中的岩浆洋初始Mg#存在差异，LPUM相对更加富镁(LPUM的Mg#为90而TWM为84)。关于月球的Mg#的讨论尚未达成一致，通过对月球样品的分析推测月球的Mg#介于80～90之间(Warren, 1985)；Armytageetal.(2012)通过对月球样品Si同位素的分析将月球Mg#限定在87～90之间；基于月球矿物成因的研究以及地月样品的氧同位素的分析则认为月球Mg#与地幔类似，应在90左右(Greenwoodetal., 2018; Haurietal., 2015; Longhi, 2006; Youngetal., 2016)。月球岩浆洋的难熔元素(如Al和Ca)组成在很大程度上影响斜长石的结晶时间和结晶比例，从而决定着最终形成的月壳厚度。TWM组分的难熔元素含量是地球地幔的1.5倍左右，而LPUM组分的难熔元素含量与地球原始上地幔相似。目前大部分针对月球岩浆洋结晶过程进行的模拟实验结果都不支持高难熔元素含量的月球组分模型(Charlieretal., 2018; Linetal., 2017a, b, 2020; Rapp and Draper, 2018)。另外，越来越多的同位素地球化学方面的研究认为月球的初始物质或许与地球同源甚至直接来自地幔(Dauphas, 2017; Dauphasetal., 2014; Toubouletal., 2007, 2009; Zhangetal., 2012)。比如，难熔元素Ti和W在月球形成的大碰撞事件之前很难达到平衡，而地月之间的Ti和W同位素组成的相似性意味着大碰撞事件使得原始地球和月球之间发生了充分的混合(Dauphasetal., 2014; Toubouletal., 2007, 2009; Zhangetal., 2012)。因此，新的月球岩浆洋演化模型多采用LPUM等与上地幔成分相似的初始物质组成(Charlieretal., 2018; Rapp and Draper, 2018)。

月球岩浆洋的深度指示了月球初始熔融的程度，决定了岩浆洋结晶分异模型采用的压力和温度参数。已有的研究对月球岩浆洋的深度估算还存在较大的不确定性，从较浅的约400km到全月幔熔融的1400km。月震数据显示在月幔500～600km处存在一个月震波速的不连续带，这可能代表了岩浆洋的底部边界(Gagnepainetal., 2006; Lognonnéetal., 2003)，但也有研究认为这一界面是岩浆洋结晶分异的结果(Khanetal., 2013)。Longhi (2006)根据月球火山玻璃源区的形成压力(>2.5GPa)，以及成分中有岩浆洋早期结晶产物的参与，推测月球岩浆洋的初始深度大于600km。还有一些研究则通过在月球核幔之间亲铁元素的分配实验推算月球核幔边界温度超过了硅酸盐矿物的液相线温度，暗示了月球岩浆洋的深度可能达到了核幔边界(Steenstraetal., 2016, 2020)。月球岩浆洋的深度取决于导致熔融发生的热源大小，主要包括形成月球的大碰撞模型所释放的能量以及短周期放射性同位素衰变等(Elkins-Tanton, 2012)。目前关于月球起源，学界比较认可的是高能量的大碰撞假说，大撞击会产生足够的热量使得月球早期发生较大程度甚至全月球的熔融(Hosonoetal., 2019; Locketal., 2018)。因此，月球形成初期具有一个全月幔熔融的岩浆洋是合理的推测。

如前所述，月壳主要由岩浆洋结晶分异形成的斜长石上浮形成，因此月壳的组成和厚度是检验岩浆洋演化模型合理性的重要指标。根据GRAIL计划获得的重力学数据反演所得月壳平均厚度为34～43km(Wieczoreketal., 2013)，是目前可信度最高的月壳厚度数据。但是，建立在实验模拟基础上的月球岩浆洋演化模型所得到的月壳厚度都无法满足GRAIL观测数据(Charlieretal., 2018; Linetal., 2017a, b, 2020; Rapp and Draper, 2018)。为了与最新观测数据获得的月壳厚度吻合，Linetal.(2017a, 2020)进行了一系列含水的月球岩浆洋结晶实验，提出水的存在可以降低斜长石液相线温度以延迟斜长石的结晶，从而降低了斜长石结晶的比例，因此可以形成较薄的月壳。但也有研究认为水的作用是有限的，而如果考虑月球深部堆积层中残留未结晶的熔体(大于10vol%)以及斜长石的上浮效率(低于80%)，则深度为600km和具有LPUM初始成分的月球岩浆洋可以结晶形成合适厚度的月壳(Charlieretal., 2018)，这一观点也得到了全月球熔融分离结晶实验的支持(Rapp and Draper, 2018)。但是，高钛月海玄武岩的形成要求月球内部残留1～2vol%的熔体，因此月幔中残留过多的熔体不是一个合理的解释(Snyderetal., 1992)。

综上所述，已有的研究支持月球的初始物质组成与地球的地幔类似，月球岩浆洋的深度可能超过1000km。但是若月球岩浆洋的结晶序列不变，已有的实验研究显示较深的月球岩浆洋结晶分异将形成较厚的月壳(>50km)，这与最新评估的月壳厚度为34～43km不符。要使月球岩浆洋结晶后形成的月壳厚度与观测结果一致，需对原有的月球岩浆洋模型中选用的参数进行合理的调整，一是月球初始物质组成方面的调整，比如降低斜长岩所需的Al和Ca等不相容元素的含量，二是形成其他含Al和Ca的矿物，比如石榴子石。Elardoetal.(2011) 以TWM和LPUM为初始物质进行了两组等压结晶实验，发现在4GPa的压力条件下，这两种初始组分的实验产物中均出现了石榴子石。石榴子石的出现表明在月幔深部可能存在一个难熔元素的储库，从而降低了岩浆中难熔元素的含量，制约了斜长石的结晶，最终形成较薄的月壳。此外，月球火山玻璃相对月海玄武岩更亏损重稀土元素(HREE)，以及低钛月海玄武岩较高的轻重稀土比值(LREE/HREE)的微量元素特征也暗示其源区可能残留石榴子石(Hallisetal., 2014; Neal, 2001)。但是，关于月幔底部深成堆积岩中含石榴子石的月球岩浆洋演化模型的研究并不系统，石榴子石在月幔深部存在的合理性需要更多的研究进行评估，同时还需要考虑不同岩浆洋深度和组分条件下石榴子石的结晶及其对月球岩浆洋演化的影响。

关于月球岩浆洋演化的实验研究，大部分采用不同压力条件下的某一种初始物质组成进行平衡或者分离结晶实验。这类实验工作需要投入大量的时间，对实验设备也有很高的要求，并且多数研究对早期月球内部的温度进行了近似处理，并未考虑矿物结晶过程中引起的温度变化。此外，由于实验压力和温度条件的限制，目前关于石榴子石结晶对月球岩浆洋演化影响的实验研究开展较少。相反，热力学计算模拟方法可以弥补上述实验方面的短板。在计算模拟中，可以通过改变几个重要的参数(如物质组成、压力等)进行不同初始条件下(物质组成和深度)月球岩浆洋的演化模拟研究，并将模拟结果与已有的探测数据和月球样品分析数据进行对比，建立符合约束条件的月球岩浆洋模型。

本文利用热力学计算模拟的方法，分别以常用的月球模型、地球地幔模型以及地球地幔橄榄岩这三类组分作为月球岩浆洋的初始物质组成，选取代表不同熔融程度的四组岩浆洋初始深度400km、700km、1000km以及1400km，模拟不同初始条件下岩浆洋的结晶分异过程并重点关注石榴石的结晶情况。在理论计算数据的基础上探讨月球岩浆洋深度、初始物质组成以及石榴子石对月球岩浆洋演化模型的影响；以最新的月壳厚度观测数据以及urKREEP成分为依据约束岩浆洋模型的初始参数；最终通过详细的正演对月球初始内部组成和结构进行模拟。

1 理论计算方法

本文所涉及的计算主要采用FXMOTR程序包(Longhi, 1991, 1992, 2002, 2006; Davenportetal., 2014)。该程序包建立在一系列实验岩石学和实验地球化学数据之上，结合了分离结晶和平衡结晶过程，可以有效地模拟岩浆洋结晶过程 (Longhietal., 2010; Snyderetal., 1992)，且与其他常用的程序包相比，FXMOTR的模拟结果与实验数据更吻合(Thompsonetal., 2003; Prissel and Gross, 2020)。

1.1 热力学计算原理

Longhi (1991, 1992, 2002)通过不同温压条件下的一系列实验，确定了橄榄石-斜长石-辉石-石英体系中液相线矿物的组成随初始成分和压力的变化规律，计算了不同成分的岩浆随温度降低所结晶的矿物种类、成分及含量，以此建立了FXMOTR程序包的基础公式。此后，Longhi针对月球岩浆洋的演化，开发并完善了主量元素在矿物晶体与残余岩浆之间分配系数的经验算法，可以计算不同矿物相的结晶温度和元素组成。

FXMOTR的计算步骤如下：(1)针对每一步微小量的结晶(通常为1mol/mol)，通过比较计算所得的岩浆成分与液相线位置，确定结晶矿物的种类和化学组成，并计算主量元素在矿物和残余岩浆之间的分配系数；(2)根据结晶开始之前的物质组成和步骤(1)所得的结晶矿物相的组成和元素的分配系数，通过质量平衡方法计算新的岩浆洋成分。上述计算步骤适用于分离结晶与平衡结晶过程，不过在计算分离结晶时，每一步结晶之前的岩浆成分取自前一个结晶周期中残余岩浆的成分，前一个周期结晶的矿物不再与新的岩浆进行元素交换。在平衡结晶中，岩浆始终与结晶的矿物进行元素交换以维持熔体与矿物间元素的平衡分配状态。

模拟计算时，先根据压力和选取的月球岩浆洋成分计算橄榄石的液相线温度，该温度作为初始温度，后由公式(1)计算矿物结晶引起的温度变化:

(1)

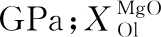
采用FXMOTR计算岩浆洋结晶分异过程时，岩浆洋的深度也随着结晶的进行发生变化。通过对每一步结晶产物的体积进行计算获得“新的”岩浆洋深度，同时调整岩浆洋底部的压力条件，结合前文所述的温度变化，自下而上模拟岩浆洋结晶的全过程。由于已有的关于月球岩浆洋结晶过程的实验模拟多数都是在几个恒定压力条件下进行的平衡结晶或者分离结晶，因此本文对FXMOTR程序进行了部分修改，使其也能够在保持压力不变的情况下进行岩浆洋结晶的模拟计算，以便将计算结果与已有的实验结果进行对比。

1.2 月球岩浆洋的结晶方式：两阶段结晶

对月球岩浆洋结晶方式的假设主要有两种：一种是从始至终的分离结晶(Rapp and Draper, 2018)；另一种是两阶段结晶，即早期以平衡结晶为主，当岩浆洋结晶到一定程度则转变为分离结晶(Elardoetal., 2011)。月球岩浆洋冷却过程中，随着温度的降低必然会发生分离结晶，但两步结晶的方式更符合岩浆洋冷却的地球物理模型。由于月球岩浆洋的瑞利数(Rayleigh number，是驱动对流的力与抑制对流的力之比)较大，约为1024～1029，据此推测在月球岩浆洋早期阶段存在对流(Tonk and Melosh, 1990)。在对流体系中，岩浆悬浮晶体的能力由劳斯数(Rouse number，晶体的末端速度与熔体的有效摩擦速度之比)表示。当劳斯数小于1，晶体将在熔体中保持悬浮，从而保持与熔体的化学平衡，此时的结晶过程为平衡结晶。在岩浆洋结晶的早期阶段，由于晶体粒度较小，劳斯数小于1，平衡结晶更符合热力学和动力学原理；当岩浆洋结晶到一定程度后，劳斯数将大于1，这时岩浆洋不能维持晶体的悬浮，从而发生分离结晶。Tonk and Melosh (1990)的计算显示，如果橄榄石是岩浆洋结晶早期的唯一固相，在400km深的岩浆洋中，平衡结晶会持续到大约50%的结晶程度，之后就会发生分离结晶。因此，多数研究选择50%的结晶程度作为两阶段结晶的分界点(Elardoetal., 2011; Linetal., 2017b)。然而，Tonk and Melosh (1990)的结论是建立在岩浆洋深度为400km并且结晶程度达到50%之前橄榄石是唯一固相的前提之下。由于月球岩浆洋深度的不确定性，辉石出现的时间及其成分对上述劳斯数等参数的影响并不清楚，因此结晶程度达到50%会出现分离结晶的结论还需要更多的实验和计算数据的验证。Snyderetal.(1992)在假设了月球热状态会维持平衡结晶至少到结晶程度达到75%的情况下进行了数值模拟研究。本文所采用的FXMOTR程序将橄榄石单独结晶的阶段设置为平衡结晶，之后为分离结晶。橄榄石单独结晶过程的比例受月球岩浆洋初始条件影响，大致为45%～60%。

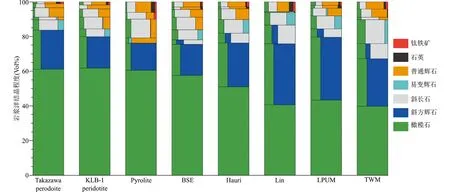
图1 不同初始成分岩浆洋的结晶序列(岩浆洋初始深度700km)Takazawa和KLB-1橄榄岩组成来自Takazawa et al. (2000)和Davis et al. (2009)；Pyrolite和BSE地球上地幔成分模型来自Ringwood (1979)以及Sun and McDough (1996)；Hauri、Lin、LPUM、TWM等月球岩浆洋成分模型分别来自Hauri et al. (2015)、Lin et al. (2017b)、Taylor (1982)和Longhi (2006)Fig.1 Crystallization sequence of lunar magma oceans with different initial compositions (the initial depth of the LMO is 700km)Takazawa and KLB-1 peridotite compositions from Takazawa et al. (2000) and Davis et al. (2009); Pyrolite and BSE Earth upper mantle composition models from Ringwood (1979) and Sun and McDough (1996); Hauri, Lin, LPUM, and TWM Lunar Magma Ocean composition models from Hauri et al. (2015), Lin et al. (2017b), Taylor (1982), and Longhi (2006), respectively

1.3 月球岩浆洋的初始成分

如前文所述，已有的研究或通过月球样品成分分析和探月观测数据的综合分析或者通过计算模拟对岩浆洋的整体成分进行约束，迄今仍未达成共识(Elardoetal., 2011; Kuskovetal., 2019; Warren, 2005)。本研究通过对前人提出的月球初始物质组成(表1)，包括Takazawa和KLB-1等天然地幔橄榄岩组分(Takazawaetal., 2000; Davisetal., 2009)、Pyrolite和Bulk Silicate Earth(BSE)等地球上地幔模型(Ringwood, 1979; McDonough and Sun, 1995)、TWM、LPUM以及Haurietal.(2015)和Linetal.(2017b)采用的月球岩浆洋模型(Taylor, 1982; Longhi, 2006; Haurietal., 2015; Linetal., 2017b)，进行详细的岩浆洋结晶演化的模拟计算，以最新的月壳厚度观测数值为基准，对月球岩浆洋的成分进行详细探讨。需要指出的是，本文采用的Takazawa组分代表一类北海道地幔橄榄岩的成分，该地幔橄榄岩的母岩浆可能形成于地幔的部分熔融，并且源区残留石榴子石(Takazawaetal., 2000)，本文用来代表地球上地幔在结晶石榴子石后残余岩浆的成分。另外，本文针对LPUM组分的月球岩浆洋，建立了一个在岩浆洋深度为1400km条件(5GPa)下石榴子石结晶后的整体岩浆洋成分(N-LPUM)，通过对这两种组分的模拟结晶研究可以探讨月幔深部存在石榴子石对岩浆洋演化的影响。

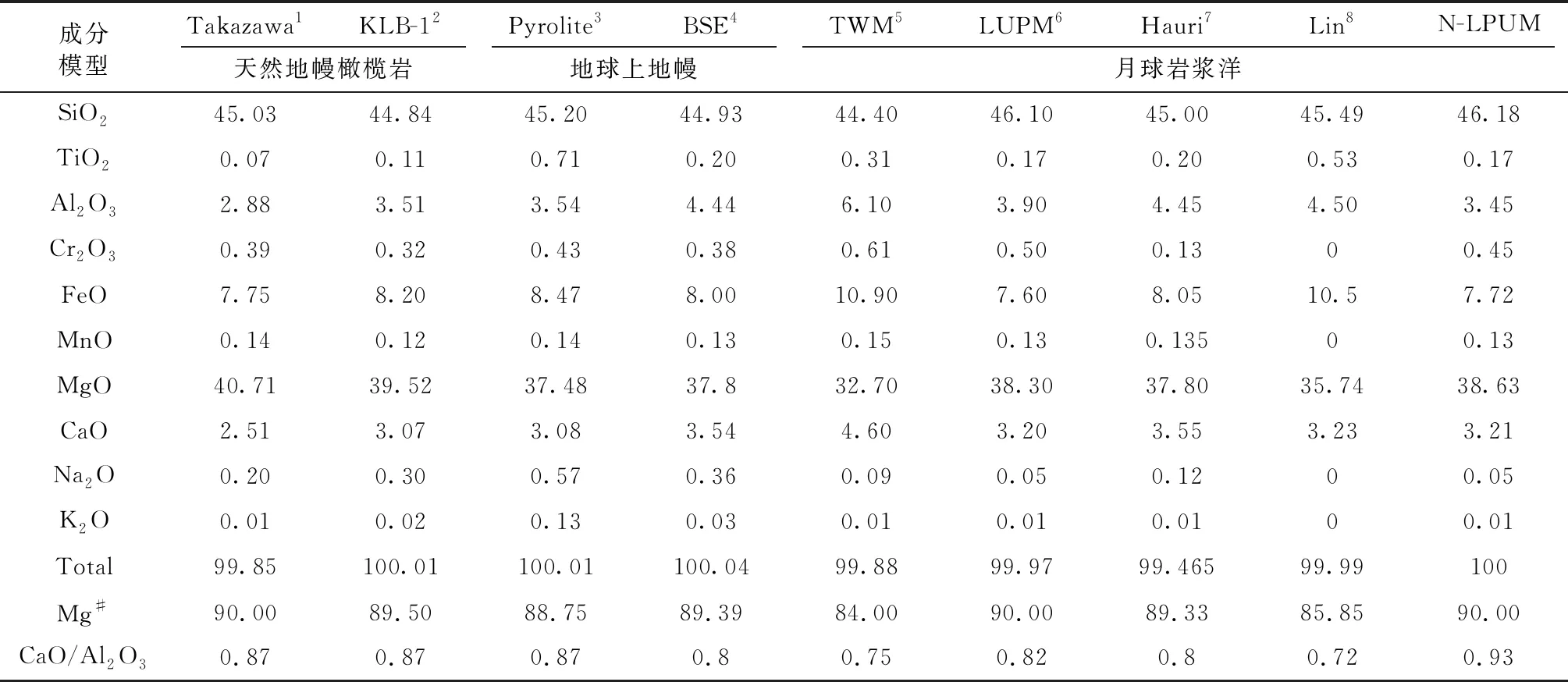
表1 本文采用的月球岩浆洋初始组成(%)

1.4 月球岩浆洋的初始深度和压力

FXMOTR程序的深度与压力关系采用Khan and Mosegaard (2002)的数据，且与月球的地球物理模型十分接近(Garciaetal., 2011)。在模拟岩浆洋演化过程中，岩浆洋的深度随着结晶矿物的堆积不断变化，因此，基于球体体积公式不断更新岩浆洋深度和底部压力，岩浆洋深度与压力换算如式(2)所示:

H(km)=-0.00029503×P4+0.02132×P3-0.25106×P2+19.6298×P+4.81969 (2)

其中，H(km)指岩浆洋的深度，P指岩浆洋底部的压力(GPa)。

本文的计算模拟包括以400km、700km、1000km、1400km为初始深度的月球岩浆洋结晶过程，覆盖了可能的岩浆洋深度范围。不同的岩浆洋深度所对应压力分别为2GPa、3GPa、4GPa和5GPa，同时本文讨论3～5GPa压力条件范围内石榴子石的结晶情况。

2 月球岩浆洋结晶过程的热力学计算结果

2.1 岩浆洋的结晶序列

本文的计算结果显示，不同初始成分的月球岩浆洋结晶序列大致相同。图1展示了岩浆洋初始深度为700km时，各种初始成分的岩浆洋的结晶序列：富镁橄榄石(Mg#约为95)作为液相线矿物最先结晶，并在很长一段时间单独结晶；之后结晶的矿物为斜方辉石，一般在结晶程度达到40%之后出现；当岩浆洋结晶达到75%左右时，斜长石在较低的温度(1200℃)和压力(0.6GPa)下开始结晶；单斜辉石的结晶过程涉及普通辉石和易变辉石两种矿物，由于普通辉石的CaO含量比易变辉石高，所以晚于易变辉石结晶，当岩浆洋结晶程度分别达到75%和80%左右时，易变辉石和普通辉石开始结晶；岩浆洋结晶到接近95%时，钛铁矿开始结晶；在钛铁矿结晶后会结晶微量的石英，这与一些实验结果能够吻合(Linetal., 2017b; Charlieretal., 2018)。大部分模拟结果都显示钛铁矿晚于普通辉石结晶，而采用Linetal.(2017b)假设的月球岩浆洋初始成分进行模拟，结果则显示普通辉石晚于钛铁矿结晶，与Linetal.(2017b)的实验观察结果一致。造成这一差异结果的主要原因是Linetal.(2017b)采用的初始成分中FeO含量偏高(10.5%)而CaO含量偏低(3.23%)，因此影响了熔体中的FeO和CaO含量，造成富集FeO的钛铁矿的提前结晶和富集CaO的单斜辉石结晶的滞后。不同初始成分的岩浆洋结晶分异过程中，除以Takazawa、KLB-1为初始物质组成的斜长石与单斜辉石同时结晶以及Pyrolite(地幔岩模型)成分中单斜辉石早于斜长石结晶外，其他成分的模拟结果均是斜长石稍早于单斜辉石结晶。

图2 不同初始深度月球岩浆洋的结晶序列(以TWM和LPUM组分为代表)Fig.2 Crystallization sequence of LMOs with different initial depths (represented by TWM and LPUM compositions)

采用FXMOTR程序模拟不同深度岩浆洋的结晶过程，发现月球岩浆洋的深度对其矿物结晶序列影响不大。两种端元初始物质组成TWM和LPUM在3GPa(700km)和4GPa(1000km)下的模拟结果显示，两种压力条件下的矿物结晶序列都是橄榄石、斜方辉石、斜长石、单斜辉石、钛铁矿和石英(图2)。只是，更深的岩浆洋(压力的增加)会造成辉石的稍早结晶，以及斜长石和石英的相对较晚结晶。例如，在TWM组分中，3GPa条件下，斜方辉石在结晶程度达到42vol%开始结晶，斜长石在67vol%开始结晶；而4GPa条件下，斜方辉石在结晶程度达到40vol%开始结晶，斜长石在68vol%开始结晶。

2.2 岩浆成分的演化

在月球岩浆洋结晶过程中，不同阶段形成的残余岩浆的成分也发生相应的变化。随着月球岩浆洋结晶分异的进行，岩浆中的MgO不断被消耗，熔体中的MgO含量从最初32%～38%降低到斜方辉石结晶时的17%～28%，到斜长石结晶时仅有10%左右，最后MgO被完全消耗。因此，残余熔体中MgO含量的变化可以代表岩浆洋的结晶程度。岩浆中的CaO和Al2O3的含量变化受辉石和长石结晶影响，也制约着月壳的主要矿物—斜长石的结晶时间和比例，而岩浆中TiO2和FeO的含量则制约了钛铁矿的结晶。岩浆洋演化到最终阶段(～99%)的残余岩浆富集K、P和稀土元素，被视为原始克里普组分urKREEP的起源(Warren, 1985; Warren and Wasson, 1979)。

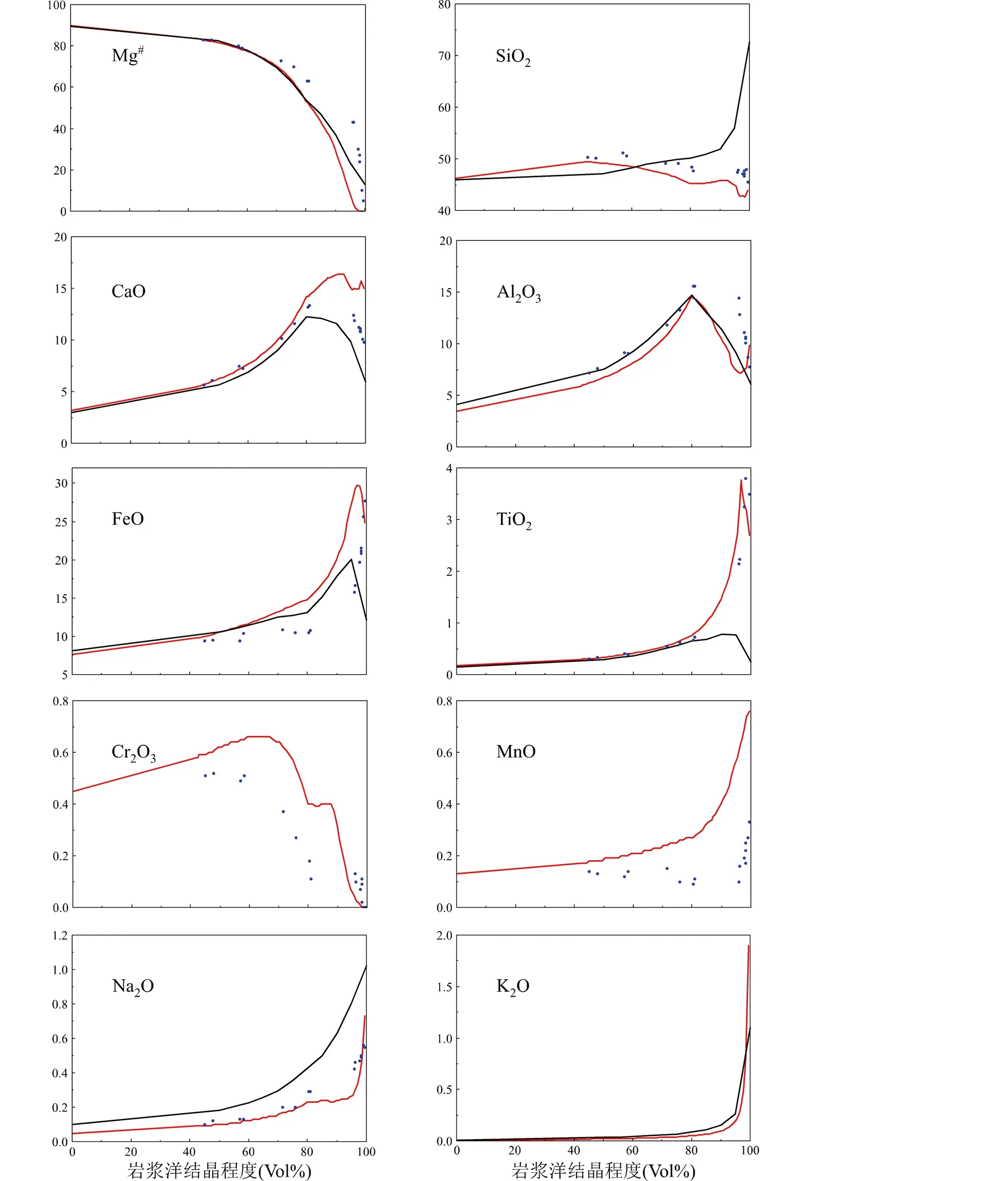
图3 月球岩浆洋结晶过程中残余岩浆成分的演化(岩浆洋的初始物质组成是LPUM，初始深度为1400km)图中氧化物成分按照质量分数给出，红色曲线代表本文数据，黑色曲线数据来自Johnson et al. (2021)的模拟结果，蓝色点数据来自Charlier et al. (2018)的实验结果Fig.3 Chemical evolution of residual LMO liquids during crystallization with percent solidified (the initial composition of LMO is LPUM and its initial depth is 1400km)The oxide composition is given in the figure by a mass fraction, the red curve represents the data in this study, the black curve data are from the simulation results of Johnson et al. (2021), and the blue dot data are from the experimental results of Charlier et al. (2018)

假设月球的初始成分为LPUM，岩浆洋的深度为1400km，结晶过程中的岩浆成分演化趋势如图3红色曲线。由于辉石和橄榄石的SiO2的含量存在明显差别，在橄榄石单独结晶阶段岩浆洋中的SiO2含量由46%上升至接近50%，在辉石结晶后回降至45%左右。斜长石的结晶对残余岩浆中的SiO2含量的变化影响不大，最后阶段由于单斜辉石的结晶造成岩浆中SiO2的含量持续下降。尽管在岩浆洋演化后期有石英的结晶，但由于不到百分之一的结晶比例，所以SiO2的变化基本不受石英的影响。由图3可见，月球岩浆洋成分的演化与斜长石、普通辉石和钛铁矿等几个关键矿物相的结晶密切相关。在斜长石结晶前，岩浆中的Al2O3和CaO均呈富集趋势。斜长石的结晶引起残余岩浆中Al2O3迅速减少，但CaO仍然呈富集趋势，只是富集的速率有所降低，在普通辉石结晶后才开始下降。可见，相对于CaO，岩浆中Al2O3的含量对斜长石结晶的时间和含量影响更大。随着岩浆洋结晶的进行，岩浆中的TiO2和FeO的含量不断增加，直到钛铁矿结晶才开始突然降低。

2.3 石榴子石的结晶

Elardoetal.(2011)以TWM和LPUM组分作为初始物质进行月球岩浆洋结晶的模拟实验，发现当实验压力超过2.5GPa，温度为1675～1800℃时，实验产物中出现了石榴子石。但是，由于石榴子石稳定的温度区间不接近任何月球成分的液相线，而且当温度降低到石榴子石的结晶区间时，岩浆洋底部的压力已经低于石榴子石的稳定区间，因此推测岩浆洋通过分离结晶方式的固化过程并不会出现石榴子石(Elardoetal., 2011)。在两阶段结晶的月球岩浆洋演化模型中，分离结晶阶段形成石榴子石的可能也很小。但是，石榴子石有可能在早期的平衡结晶阶段形成并留在月球深部。然而，由于FXMOTR程序包虽然采用平衡结晶的元素分配模式模拟月球岩浆洋演化早期的橄榄石结晶，但是在计算压力时仍然按照分离结晶的模式，即随着结晶程度的增加，岩浆洋底部的压力逐渐降低，因此采用该程序包对不同物质组成和深度的月球岩浆洋结晶模拟计算都没有出现如Elardoetal.(2011)报道的石榴子石。

为了更好的与实验结果进行类比，本文改进了FXMOTR程序包，使其能够模拟恒压结晶过程并计算高压条件下石榴子石结晶的温压条件以及含量。由于岩浆洋早期阶段结晶的石榴子石主要是镁铝榴石，其密度(3.6～3.7g/cm3)大于富镁的橄榄石(3.3～3.4g/cm3)，而且其结晶顺序在橄榄石之后，因此本研究中将石榴子石的结晶方式设置为分离结晶，即在岩浆洋的平衡结晶阶段，少量的石榴子石随着结晶不断与残余岩浆分离。本次研究以最具代表性的两种月球岩浆洋的物质组成——TWM和LPUM组分作为初始成分，模拟了3GPa、4GPa、5GPa压力下岩浆洋结晶过程(对应的岩浆洋深度分别为700km、1000km和1400km)。模拟结果显示：(1)在TWM组分的岩浆洋中，3GPa、4GPa和5GPa压力下石榴子石的液相线温度分别为1461℃、1631℃和1779℃；(2)对于LPUM组分的岩浆洋，3～5GPa压力下石榴子石的液相线温度分别为1439℃、1612℃和1833℃。修正后的FXMOTR程序模拟固定压力条件下的月球岩浆洋结晶序列结果与Elardoetal.(2011)的实验结果接近。TWM组分的岩浆洋中石榴子石的结晶要早于LPUM组分的岩浆洋，在TWM组分中，压力达到4.5GPa时，石榴子石作为第二种矿物相在橄榄石之后结晶，而在LPUM组分中，压力达到5GPa时石榴子石才作为第二种矿物相结晶。TWM组分的岩浆洋在3GPa、4GPa和5GPa压力时分别结晶出1%、2%和3%的石榴子石；LPUM组分结晶的石榴子石比例较低，分别为0.5%、1%和2.5%。关于石榴子石对岩浆洋演化的影响将在下一章节进行详细讨论。

3 讨论

3.1 模拟计算结果与已有的月球岩浆洋结晶实验结果对比

除了Linetal.(2017b)的实验中观察到斜方辉石与橄榄石在实验开始时就一同结晶外，本次模拟计算得到的月球岩浆洋结晶序列与大部分月球岩浆洋演化的实验结果一致，即橄榄石作为第一液相线矿物结晶，并在一定的温压条件下单独结晶。造成这种差异的主要原因是Linetal.(2017b)选取了一个较低的月球岩浆洋温度，并对月球深部的物理环境进行了简化，即假设了月球岩浆洋的对流十分强烈，并因此选取了阶段等温的实验条件。这种较低温度的设定在某种程度上有悖于大碰撞假说的高能环境，也与通过MELTs计算所得的月球地温梯度趋势不符(Elkins-Tantonetal., 2011; Mauriceetal., 2020)。本文通过橄榄石的液相线温度确定岩浆洋的初始温度，并且岩浆洋的内部温度随深度和结晶程度不同而变化(图4a)，初始温度接近月球内部初始温度梯度(Elkins-Tanton, 2012)，在其它初始参数与Linetal.(2017b) 完全一致的情况下进行了岩浆洋结晶的模拟计算。本次模拟计算发现，橄榄石仍然是第一液相线矿物单独结晶，之后才是橄榄石和斜方辉石的共结晶，这与Linetal.(2017b)的实验中观察的结晶序列不同(图4b)。另外，本次模拟中斜长石的比例也低于Linetal.(2017b)的实验结果，由此计算所得的月壳厚度是49.4km，小于Linetal.(2017b)推算的67.5km。造成这一差异的原因可能是Linetal.(2017b)采用的初始温度较低，导致斜长石结晶提前且比例增加。

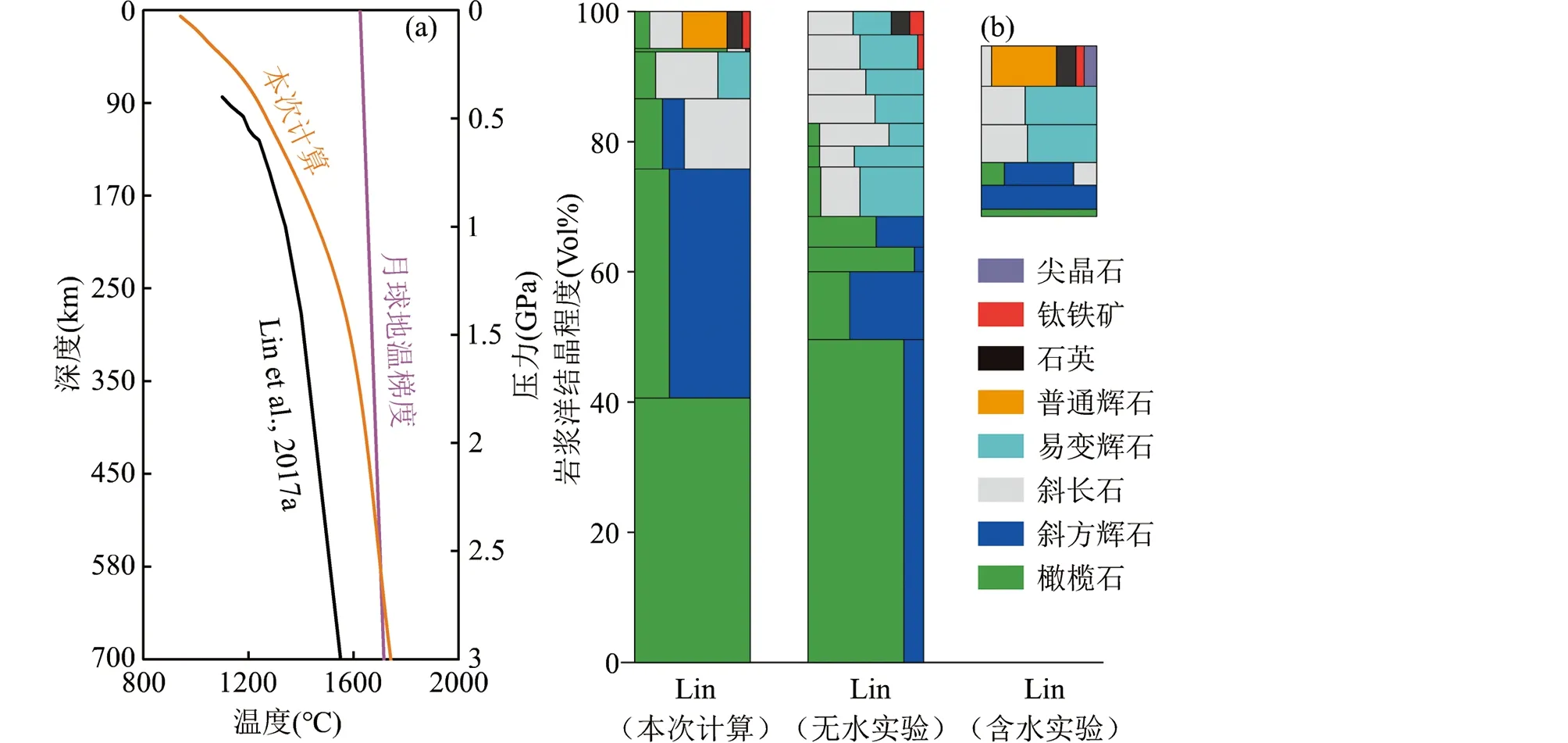
图4 温度和水对月球岩浆洋结晶序列的影响(a)与先前研究的月球地温梯度对比；(b)与先前含水实验和无水实验结果的对比. 无水实验数据来自Lin et al. (2017b)，含水实验数据来自Lin et al. (2017a)，月球地温梯度来自Elkins-Tanton (2012)Fig.4 Effect of temperature and water on the crystallization sequence of the LMO(a) comparison of lunar geothermal gradients between this study and previous study; (b) comparison with the results of previous anhydrous and hydrous experiments. The data of the anhydrous experiment is from Lin et al. (2017b), hydrous experimental data from Lin et al. (2017a), and lunar geothermal gradients from Elkins-Tanton (2012)

另一方面， Linetal.(2017a)进行了含水的月球岩浆洋结晶模拟实验，该实验相当于在Linetal.(2017b)无水实验的初始物质(即表1中的Lin组分)中多加入了1%的水。水的存在会降低矿物的液相线温度，但是水对不同矿物的液相线温度影响不同。如果体系内的水含量是1%，橄榄石的液相线温度下降约75℃，斜长石的液相线温度下降约120℃(Danyushevsky, 2001)，而辉石的液相线温度降低幅度介于橄榄石与长石之间，约100℃(Métrich and Rutherford, 1998)。因此，Linetal.(2017a)的含水实验中出现了橄榄石单独结晶的阶段，并且出现了无水实验中没有观察到的普通辉石。其结果与本文的计算结果较为接近，单斜辉石晚于斜长石结晶，普通辉石出现的节点也与模拟结果类似(图4b)。

本文的模拟计算结果与前人实验研究结果较大的差别在于斜长石与单斜辉石结晶顺序的不同，已有的实验研究结果均显示单斜辉石与斜长石两者同时结晶，并没有出现斜长石早于单斜辉石结晶的现象(Linetal., 2017b; Charlieretal., 2018; Rapp and Draper, 2018)。然而本文的模拟结果显示，大多数岩浆洋初始成分的结晶序列中斜长石先于单斜辉石结晶，之后是斜长石和单斜辉石共同结晶，这与采用THERMOCALC3.50软件包以LPUM为初始成分进行的热力学计算研究结果相一致(Johnsonetal., 2021)。本文在以Takazawa、KLB-1组分作为岩浆洋初始成分的模拟结果中也存在单斜辉石与斜长石共结晶的情况，并且Pyrolite组分的模拟结果中单斜辉石早于斜长石结晶。根据本文的模拟结果推测，斜长石和单斜辉石结晶顺序的差别主要是因为岩浆洋成分的Al2O3和CaO含量差异造成其结晶路径不同，同时也受到Na2O和K2O含量的影响。在CaO含量较低和Al2O3含量较高时(CaO/Al2O3<0.87左右)，结晶路径将首先经过斜长石单独结晶区间；而Na2O和K2O含量的增加将改变单斜辉石和斜长石的液相线，尽管两者的结晶区间都会被扩大，但单斜辉石的结晶区间增加的更多(Longhi and Pan, 1988; Longhi, 1991)。因此，在碱元素和CaO含量更高的成分中单斜辉石将更早结晶。

采用相同初始成分的计算结果与实验结果之间的不一致性也可能与两种方法模拟分离结晶的过程有关。在实验模拟中通常采取较大的结晶分数间隔来模拟分离结晶的进行，例如Rapp and Draper (2018)在模拟分离结晶的第7阶段出现了斜长石，同时也有单斜辉石(Wo=5)出现。但第7阶段开始时的结晶程度为74%，结束时结晶程度为88%，之间具有14%的结晶间隔。因此，该实验无法证明结晶程度在74%到88%之间是否有斜长石单独结晶，不能明确区分这两种矿物的结晶节点。本文采用与之相同初始压力(4GPa)和初始成分(LPUM)进行模拟，结果显示岩浆洋在结晶程度为77%时斜长石开始结晶，结晶程度为82%时单斜辉石和斜长石共同结晶，这些都是在实验的结晶区间内发生的，因此实验中斜长石的结晶也可能是早于单斜辉石结晶的。这一部分的差异可以通过更细致的结晶实验进行验证。

图3对比了本文与Johnsonetal.(2021)的计算模拟结果以及Charlieretal.(2018)的实验模拟结果中随着岩浆洋演化残余岩浆成分的演化趋势。不同的结果显示，残余岩浆成分的演化趋势大体一致，但本文的计算结果在SiO2和TiO2上与Johnsonetal.(2021)的模拟结果存在较大差异。Johnsonetal.(2021)的模拟结果中，残余岩浆的SiO2含量呈富集趋势，在结晶的最终阶段残余岩浆中SiO2含量达到了72.6%，并结晶0.85vol%的石英相，但实验研究中石英相的结晶比例仅在0.1vol%左右(Charlieretal., 2018)。而Johnsonetal.(2021)的模拟研究中低钙辉石与熔体间TiO2的分配系数大于1，导致其模拟结果中残余岩浆的TiO2含量低于本文模拟结果以及Charlieretal.(2018)的实验结果。本文计算的结晶顺序是斜长石早于单斜辉石，而残余岩浆中的Al2O3和CaO含量分别在斜长石和单斜辉石结晶开始时降低。Charlieretal.(2018)的实验结果中，斜长石与单斜辉石共同结晶，Johnsonetal.(2021)的热力学模拟结果与本文类似，同样是斜长石早于单斜辉石结晶，因此分别表现为残余岩浆中的Al2O3和CaO的变化趋势同步降低和不同步降低。尽管已有的月球样品指示月壳的主要组成矿物是钙长石，但不同的计算模拟和实验结果均显示，在月球岩浆洋演化中，相较于CaO，斜长石的结晶与岩浆中的Al2O3含量关系更为密切，推测月球初始物质组成中的Al2O3含量对岩浆洋结晶形成的月壳厚度影响更大。

3.2 岩浆洋初始成分和深度对月壳厚度的影响

斜长石是月壳最主要的组成矿物，简化的月球岩浆洋结晶模型认为斜长石全部上浮形成月壳。但是，如前文所述，月球高钛玄武岩的微量元素特征指示月球深部堆积层含有约1～2vol%的残留熔体，且斜长石上浮效率约为90%(Snyderetal., 1992)。Suckaleetal.(2012) 从岩浆洋的粘滞性出发，认为如果分选效率低于87%，则斜长石将无法上浮。因此，本文假设岩浆洋结晶形成的斜长石有90%上浮形成月壳，并以此计算月壳厚度。通过模拟多个不同岩浆洋的结晶过程，得到一系列的月壳厚度，并通过最小二乘法探讨了岩浆洋初始深度和成分与月壳厚度的数值关系。

如果不考虑高压矿物(比如石榴子石)的结晶，不同初始成分的月球岩浆洋的结晶序列并不随深度发生改变；形成的月壳厚度与岩浆洋初始深度的关系可以用一个误差非常小的二次函数来表示。该函数关系的二阶导数小于零，表明月壳厚度随着岩浆洋初始深度增加的速度而降低。例如，当岩浆洋的初始成分与LPUM一致时，月壳厚度与岩浆洋深度的关系可以由以下拟合函数表示:

D=-4.0037×10-6×h2+0.08785×h+0.07831

(3)

其中D代表月壳厚度(km)，h代表岩浆洋初始深度(km)，回归系数R2=0.9995。月壳厚度与初始深度的关系呈非线性的正比关系，其变化趋势受岩浆洋体积变化以及压力变化的影响。一方面，由球体几何可以推断随着岩浆洋深度的增加，岩浆洋的体积所增加的幅度是非线性函数关系，这决定了(3)式中各项系数的正负；另一方面，随着岩浆洋深度的增加，辉石结晶的压力范围得到了扩展，影响了残余岩浆洋中的Al2O3含量，这可能略微影响斜长石结晶的比例，从而影响月壳的厚度。

不同初始物质组成的月球岩浆洋结晶形成的月壳厚度随岩浆洋初始深度的变化趋势一致，但成分相同、初始深度不同的岩浆洋所结晶形成的月壳厚度存在明显差异(图5)。根据初始物质组成中Al2O3含量的高低大致分成三类：相对地幔铝含量富集的组分，以TWM为代表；相对地幔铝含量基本一致的组分，以LPUM为代表；相对地幔铝含量亏损的组分，以Takazawa橄榄岩为代表。如果月球岩浆洋的深度为1000km，富集的月球(TWM)结晶形成的月壳厚度达到85km，而亏损的月球(Takazawa)形成的月壳厚度只有40km。如果以GRAIL探测数据估计的34～43km的月壳厚度作为参考依据，TWM代表的富集月球的岩浆洋深度只有约300km，以LPUM为初始物质组成的月球岩浆洋的深度约为750km；而如果月球的组成与相对亏损的Takazawa橄榄岩相似，则其岩浆洋的深度可以达到1000km，甚至达到月球的核幔边界。

图5 岩浆洋初始深度与月壳厚度的关系灰色区域表示地球物理数据约束的月壳厚度34～43km(Wieczorek et al., 2013).每条曲线代表不同的物质组成，具体参考表1Fig.5 Relationship between the initial depth of LMO and the thickness of the lunar crustThe grey area represents the lunar crust thickness constrained by geophysical data (34～43km) (Wieczorek et al., 2013). Each of the different lines represents different starting composition, referring to Table 1 for more details

月壳厚度主要取决于岩浆洋结晶的斜长石的含量，由残余岩浆洋成分的变化趋势(图3)可以推测其初始成分中的Al2O3含量对月壳厚度的大小起决定性作用。假设月球岩浆洋的深度为700km，通过对月壳厚度与不同初始物质组成中Al2O3含量的数值关系研究，可以得到以下的线性关系式:

D=11.6873×C+0.1714

(4)

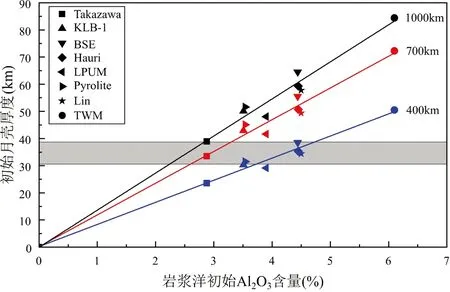
图6 岩浆洋初始Al2O3含量与岩浆洋结晶形成的月壳厚度的关系灰色区域表示地球物理数据约束的34～43km月壳厚度(Wieczorek et al., 2013). 岩浆洋初始深度分别为400km、700km和1000kmFig.6 Relationship between the initial alumina content of magma ocean and the thickness of lunar crust formed by crystallizationThe grey area represents the 34～43km lunar crust thickness constrained by geophysical data (Wieczorek et al., 2013). The initial depths of LMO are 400km, 700km and 1000km, respectively

其中D代表月壳厚度(km)，C代表岩浆洋初始Al2O3含量(%)，回归系数R2=0.9780。尽管Al2O3含量与月壳厚度存在直接的正相关关系，但从模拟结果中可以看出，Al2O3含量相似的岩浆洋所结晶的月壳厚度存在一些不符合这种线性关系的情况，暗示了月球初始物质组成中的其它成分也可能对斜长石的结晶有影响(图6)。例如Pyrolite组分与KLB-1组分的Al2O3含量几乎一致(～3.5%)，但Pyrolite组分结晶分异形成的月壳相对要厚5%左右。本文的计算结果显示相比KLB-1组分，Pyrolite组分更早结晶普通辉石、斜长石及钛铁矿。因为Pyrolite组分具有更高的TiO2(0.7% vs. 0.11%)、Na2O(0.57% vs. 0.30%)以及K2O含量(0.13% vs. 0.02%)，而(1)Na2O和K2O含量的增加会扩大斜长石的结晶区间，因此影响到斜长石的结晶比例(Longhi, 1991)；(2)TiO2的含量控制着钛铁矿的形成，而钛铁矿相对其它矿物具有更低的标准摩尔生成焓(Holland and Powell, 2011)，因此更高的TiO2含量导致钛铁矿更早的结晶，造成该阶段的结晶潜热相对较低而岩浆洋的温度下降得更快，从而促进斜长石的结晶，最终形成较厚的月壳。同理可见，即使LPUM组分中的Al2O3的含量相对更高(3.9%)且Mg#也更高(90)，但是FeO含量只有7.6%，TiO2含量只有0.17%，Na2O和K2O含量在这三者中也是最低的，分别为0.05%和0.1%，因而其结晶形成的月壳厚度是最薄的。综上，月球初始月壳厚度尽管主要受岩浆洋初始组分中的Al2O3含量的制约，但其它元素的含量也会在一定程度上影响斜长石的结晶比例。

3.3 石榴子石结晶对月球岩浆洋演化的影响

月球深部是否存在石榴子石是实验和计算模拟月球岩浆洋演化过程中争论较大的问题。由于石榴子石属于高压的富Al矿物且相对富集重稀土，其在月球深部存在与否直接关系到月球岩浆洋初始物质组成及深度的限定。由于缺乏月球深部的样品，目前关于月幔深处存在石榴子石的推测均依赖间接证据，包括对月海玄武岩、月球火山玻璃的研究以及地震学数据的反演等方面研究结果，这些结果支持月幔深部存在一个石榴子石储库(Kuskovetal., 2019)。Neal (2001)认为月球火山玻璃相对于月海玄武岩亏损HREE，其原因可能是火山玻璃的源区存在石榴子石残留。Barr and Grove (2013)根据Apollo 15A绿色火山玻璃的主量和微量元素含量推测其母岩浆具有来自石榴子石二辉橄榄岩发生熔融形成的熔体的参与。Hallisetal.(2014)认为低钛月海玄武岩具有相对较高的La/Lu比值(>2.4)，暗示了其源区中存在石榴子石。另一方面，Elardoetal.(2011)实验确定的石榴子石结晶压力区间在2.5GPa以上，所对应的岩浆洋深度大于600km，那么目前学界比较认可的全月幔熔融将形成满足石榴子石结晶温压条件的岩浆洋。如果石榴子石能够作为一个稳定的矿物出现，将在很大程度上控制岩浆洋中的Al2O3含量，制约斜长石的结晶，从而解释较深的岩浆洋结晶“较薄的”月壳的问题。

本文的计算结果显示，月球岩浆洋深部结晶出的石榴子石主要是镁铝榴石，尽管含量较少，但是其Al2O3的含量超过22%，将会显著降低残余岩浆洋中的Al2O3含量。比如，LPUM组分的岩浆洋在5GPa的情况下会结晶2.5%左右的石榴子石，结合石榴子石的元素含量以及结晶比例，LPUM组分的残余岩浆洋的Al2O3含量从3.9%下降至3.45%，而其它元素含量基本没有变化。基于此，本文建立了一个N-LPUM组分，代表这一条件下石榴子石结晶后的岩浆洋成分。由于石榴子石结晶降低岩浆洋中的Al2O3含量使得岩浆洋结晶出更薄的月壳，在岩浆洋深度为1400km的情况下，N-LPUM组分(44.61km)所结晶的月壳厚度相比较LPUM组分(51.72km)降低了7.11km。而TWM组分结晶的石榴子石比例尽管更大，但由于其初始Al2O3含量过高，即使在结晶了足够多的石榴子石后，N-TWM组分Al2O3含量(5.6%)也远高于其它组分，因此仍然无法满足月壳厚度的约束。

Hallisetal.(2014)认为月幔深部存在0.5%的石榴子石便能满足月海玄武岩的La/Lu比值，而本文在5GPa下的岩浆洋结晶出了2.5%的石榴子石。Hallisetal.(2014)使用的石榴子石与熔体间的微量元素分配系数来自Greenetal.(2000)，该分配系数基于的石榴子石的成分中FeO和CaO的含量都较高，与本次计算和前人实验中得到的石榴子石成分相差较大，结晶条件也不一致(表2)，因此Greenetal.(2000)的分配系数可能并不适用于月球岩浆洋微量元素演化的讨论。本文采用的石榴子石与熔体间分配系数的数值模型建立在石榴子石晶格结构的基础上，可以针对石榴子石成分的不同进行相应的分配系数的计算调整(Sun and Liang, 2013a)。本文计算的在月球岩浆洋中微量元素在石榴子石和熔体之间的分配系数与Greenetal.(2000)的数据有所差别，推测由石榴子石引起的轻重稀土的分馏程度相对较低(表2)。但考虑本次模拟结果石榴子石含量为2.5%，高于Hallisetal.(2014)所推测的0.5%，因此，残余岩浆中的微量元素含量仍可以满足月海玄武岩的微量元素特征，即月海玄武岩的母岩浆可能是月球岩浆洋结晶石榴子石后的残余岩浆。反之，如果这些月海玄武岩的成因是月幔翻转引起的深部物质熔融而将石榴子石的信号带入到月球浅表，考虑到石榴子石并不是液相线矿物，那么深部月幔的熔融程度可能相对较低，熔体上升的动力学驱动需要重新思考。

3.4 满足月壳厚度约束的月球岩浆洋参数

本文的计算结果显示，不同成分的岩浆洋都在结晶程度达到75%前后开始结晶斜长石，并上浮形成一个初始月壳。最近的GRAIL任务的分析结果将月壳平均厚度限制在34～43km(Wieczoreketal., 2013)，而实验和计算模拟结果所结晶的月壳都高于目前观测结果所限定的月壳厚度，需要进一步的解释以满足观测数据的约束。如前文所述，为了更好地

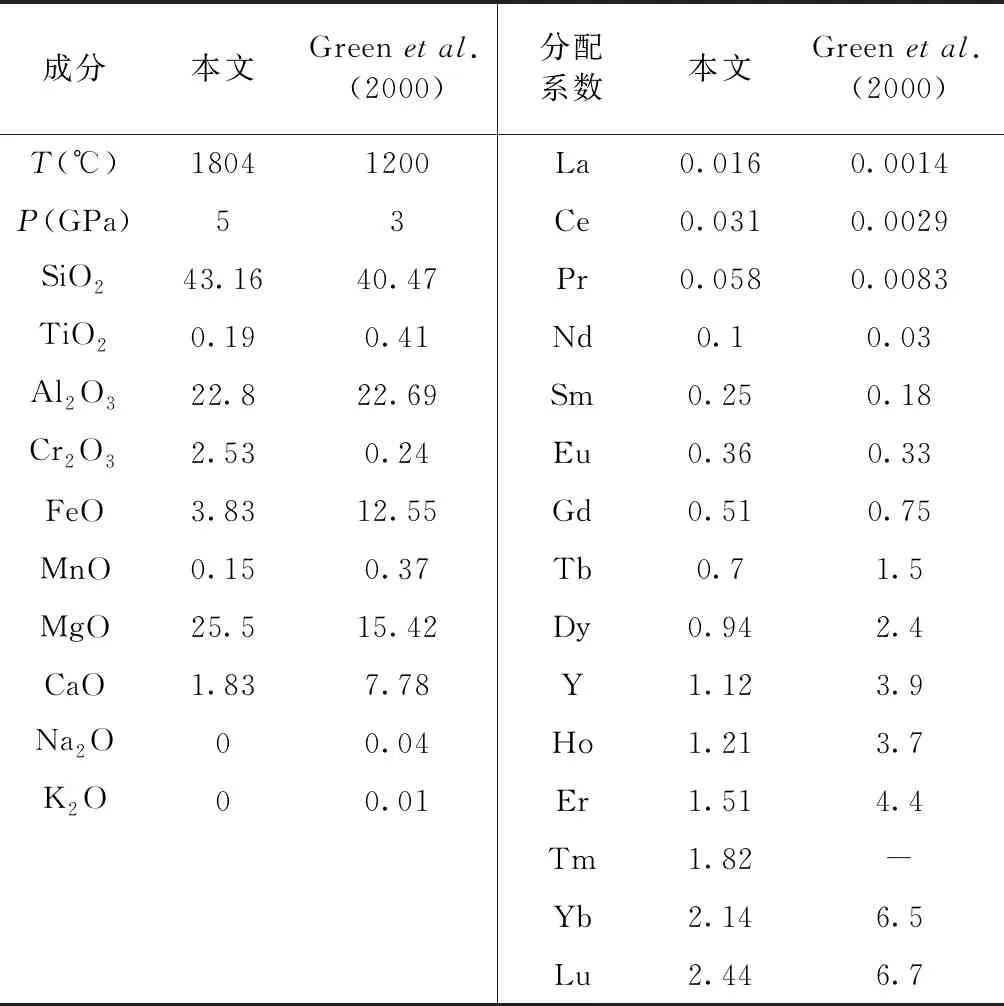
表2 本文与前人研究采用的石榴子石成分(%)以及微量元素在石榴子石与熔体间的分配系数

解释月球样品的高钛玄武岩的微量元素特征，Snyderetal.(1992)认为在岩浆洋演化过程中存在1vol%～2vol%的岩浆没有结晶而是以残留熔体的形式保留在月幔中。之后的研究认为，在残留熔体的比例达到10%以及斜长石的分选效率低到80%的极端条件下将会结晶出一个符合约束厚度的月壳(～40km)(Charlieretal., 2018; Rapp and Draper, 2018)。但是，较低的斜长石分选效率以及较高的残留熔体比例将会导致岩浆洋结晶矿物的微量元素异常，不能形成一个微量元素含量合适的玄武岩源区(Snyderetal., 1992)，而针对斜长石分选效率的模拟计算研究也支持斜长石的高效率分选(Suckaleetal., 2012)。另一方面，Linetal.(2017a, b, 2020)的研究认为月球内部水的存在导致斜长石液相线温度降低，推迟了斜长石的结晶，并且在斜长石结晶前，岩浆洋将结晶更多的辉石，降低了残余岩浆中的Al2O3含量，从而结晶更少的斜长石，最终形成一个较薄的初始月壳。然而，也有研究提出斜长石液相线的降低和辉石的结晶对斜长石结晶的影响是有限的，不能够很好地解释月壳厚度的变化(Charlieretal., 2018)。在本文所得到的一系列模拟结果中，TWM组分在任何岩浆洋深度都不能结晶出符合观测数据厚度的月壳。对于Al2O3含量介于LPUM和TWM组分的初始成分(表1)，在400km深度时可以结晶出较薄的月壳厚度(34～38km)，落在GRAIL探测结果推算的月壳厚度范围之内，即一个具有类似Linetal.(2017b)的初始成分的较浅的月球岩浆洋，能够形成满足上述厚度条件的月壳(图5、图6)。但是，月球火山玻璃的源区可能是由岩浆洋早中期堆积物(橄榄石+斜方辉石)和晚期堆积物的混合，并在2.5GPa以上的压力下发生部分熔融形成，该压力条件下相对应的岩浆洋深度大于600km，所以一个较浅的岩浆洋将无法解释这些月球火山玻璃样品的成因(Longhi, 2006)。对于以LPUM组分为代表的与地球原始上地幔成分类似的组分，700km深的岩浆洋结晶可以形成符合厚度约束的月壳。如果考虑月球大碰撞模型支持的全月幔熔融的情况，则只有在原始地幔成分结晶石榴子石后的残留熔体成分(Takazawa)能结晶形成符合GRAIL约束的月壳厚度。

在3.2部分讨论中，模拟结果显示在月球岩浆洋不存在石榴子石结晶的情况下，初始深度越深所结晶的月壳越厚。但是，如果岩浆洋的深部结晶出一定量的石榴子石，将会降低岩浆洋中的Al2O3含量，从而使得一个月幔全熔融的岩浆洋仍然能够满足月壳厚度的约束。本文结合先前针对岩浆洋结晶石榴子石的讨论，进一步讨论了LPUM和TWM组分的岩浆洋受石榴子石的影响。TWM组分的岩浆洋，尽管其能够结晶出更多的石榴子石，但在任何可能的深度条件下，仍然不能结晶出一个符合GRAIL约束的月壳厚度。LPUM组分的岩浆洋在1400km的深度下结晶出2.5%的石榴子石，残余岩浆的Al2O3含量降低为4.5%，所结晶的斜长石比例为8.4%，形成了44.61km的月壳。如果考虑堆积层中可能存在1vol%～2vol%的残留熔体，月壳厚度将下降1～2km，完全符合GRAIL结果的约束。同时，以类似地球原始上地幔成分的LPUM组分作为岩浆洋的初始成分将满足同位素对地月组成相似性的制约，而1400km的岩浆洋深度也符合月球的高能大碰撞起源假说导致全月幔熔融的推测。

综上所述，如果月球初期处于全月熔融状态，即月球岩浆洋初始深度达到核幔边界，并且其初始物质组成与地球原始上地幔相似(LPUM)，那么月球岩浆洋结晶过程早期将形成约2.5%的石榴子石，经过结晶分异最终形成的初始月壳平均厚度满足GRAIL观测数据的约束。

3.5 岩浆洋残余熔体成分演化—urKREEP的约束

KREEP岩是富含不相容元素的一类月球样品，它的微量元素含量模式被认为代表了月球岩浆洋结晶最终阶段熔体(urKREEP)的微量元素特征。尽管目前没有这种残余熔体的直接样品，但如果KREEP岩确实与岩浆洋的结晶分异有关，那么在模拟的岩浆洋结晶最后阶段应该产生与urKREEP类似的残余熔体。由于月球样品收集的局限性，目前对urKREEP的元素组成的研究非常有限。如表3所示，Neal and Taylor (1989) 提出了两种可能代表urKREEP熔体的主量元素成分，可以与本次模拟的岩浆洋结晶最终阶段的残余熔体进行对比。

本文的计算模拟结果显示，初始成分为LPUM组分，深度达到月球核幔边界的月球岩浆洋，结晶分异最终阶段的残余熔体富含FeO、CaO、Al2O3、TiO2以及K2O和Na2O，仅含有0.01%的MgO(表3)。残余熔体密度约为3.15g/cm3，大于月壳密度但小于后期结晶的含钛铁矿层密度，单独由该层堆积物密度差异驱动的翻转不太可能将其推入月幔中。模拟所得的最终熔体成分中SiO2、TiO2、Al2O3和FeO的含量与urKREEP成分能够很好的匹配，Na2O、K2O和MgO差异也较小，只有CaO的差异较大。如果考虑KREEP玄武岩样品可能受各种复杂的过程影响，其组成变化很大(Korotevetal., 2011)，那么本次研究的模拟结果与推测的urKREEP成分之间的差异在可接受范围之内。

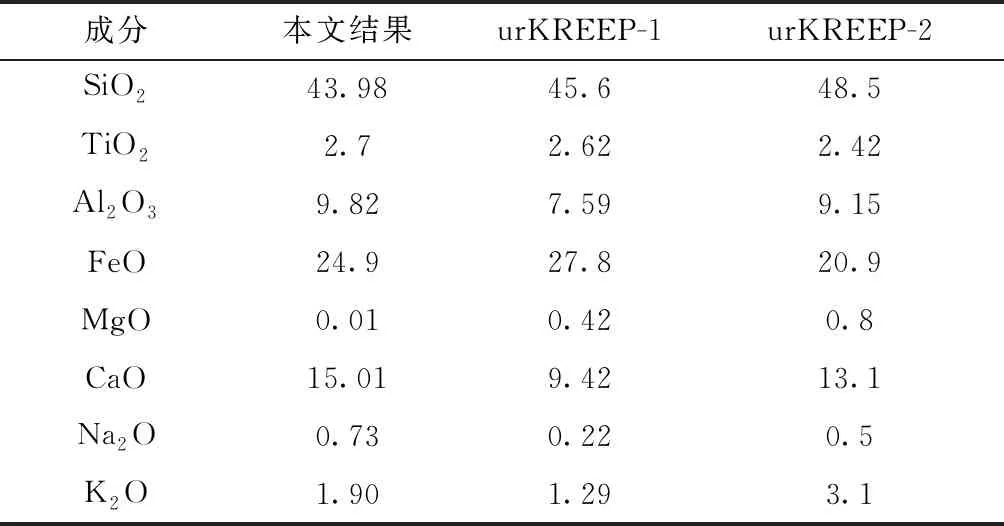
表3 月球岩浆洋结晶最终阶段残余熔体成分(%)的模拟结果和可能的urKREEP成分对比(据Neal and Taylor, 1989)

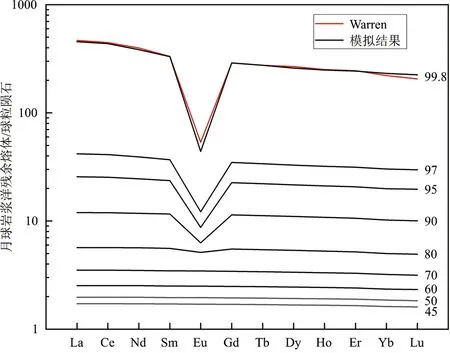
图7 月球岩浆洋残余熔体中稀土元素组成随结晶进行的变化岩浆洋微量元素以碳质球粒陨石作为初始成分. 数字代表岩浆洋结晶程度，黑线曲线代表模拟的稀土元素丰度，红色曲线代表warren (1979)认为的urKREEP稀土元素丰度，碳质球粒陨石数据来自Anders and Grevesse (1989)Fig.7 The evolving REE composition of the residual melts with the crystallization of a LMOLMO trace elements use carbonaceous chondrite as the initial component. The numbers represent the degree of magma ocean crystallization, the black curve represents the simulated rare earth element abundance, and the red curve represents the urKREEP rare earth element abundance according to warren (1979), and the carbonaceous chondrite data are from Anders and Grevesse (1989)

另一方面，urKREEP被认为是极富不相容元素的残余熔体。通过对比月球岩浆洋结晶分异形成的残余熔体与urKREEP的稀土元素含量，可以对月球岩浆洋演化过程进行约束。本文采用碳质球粒陨石的微量元素组分作为月球的初始微量元素组成(Anders and Grevesse, 1989)，结合不同矿物与熔体之间的稀土分配系数模型，包括橄榄石和石榴子石(Sun and Liang，2013a)、斜方辉石(Sun and Liang, 2013b)、单斜辉石(Dygertetal., 2014)以及斜长石(Sunetal., 2017)，计算岩浆演化过程中的稀土含量变化，建立了月球岩浆洋稀土元素的演化模型。如图7所示，在岩浆洋结晶早期，由于石榴子石对稀土元素分馏的特性，熔体相对富集轻稀土元素。稀土元素在橄榄石和斜方辉石中均高度不相容，因此在斜长石和普通辉石开始结晶之前，稀土元素几乎没有进一步分馏。斜长石结晶后，由于Eu元素更倾向分配进斜长石中，熔体开始出现Eu的负异常特征。在岩浆洋结晶后期，由于高钙辉石的分馏作用，熔体更富集轻稀土元素。岩浆洋结晶到99.8vol%时，残余熔体与可能的urKREEP稀土元素丰度基本一致，残余熔体相当于1.5km厚度的富稀土元素层。因此，如果月球的微量元素组成与碳质球粒陨石相当，熔融深度达到核幔边界的LPUM组成的月球岩浆洋，通过结晶2.5%的石榴子石对轻重稀土进行分馏，岩浆洋结晶最后阶段形成的熔体的化学组成与urKREEP非常接近。

3.6 月球初始内部成分与密度结构

初始成分为LPUM组分，深度达到1400km的月球岩浆洋结晶过程的模拟结果既满足了最新的月壳平均厚度探测数据的约束又符合urKREEP成分的要求，对认识月球初始内部结构也有很大帮助。本文针对这一参数组合的月球岩浆洋以1%为结晶间隔进行了岩浆洋结晶过程的模拟，得到了一个详细的月球内部初始结构(图8)。

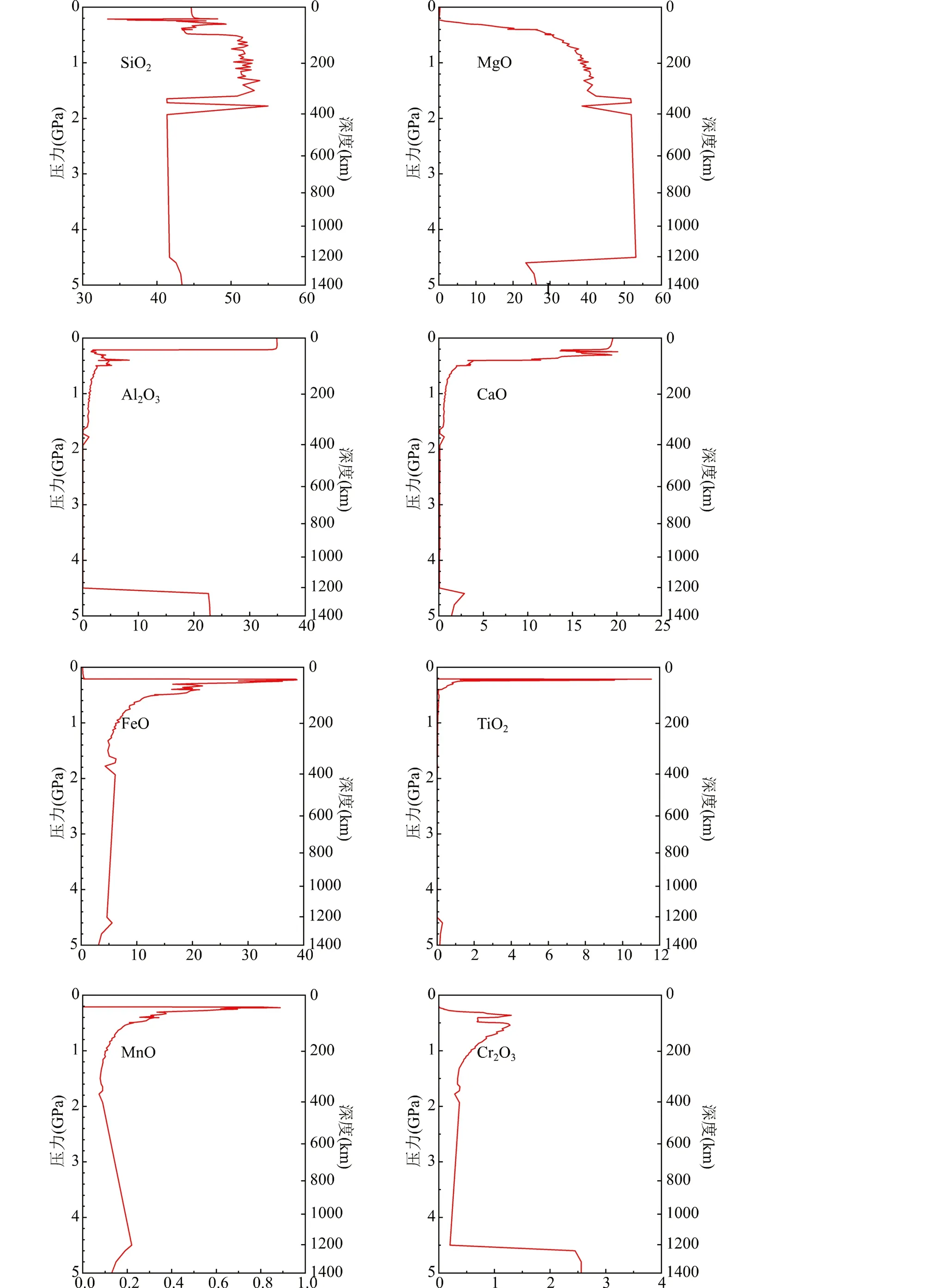
图8 月球岩浆洋结晶形成的月球初始内部组成岩浆洋初始深度为1400km，初始成分为LPUM组分Fig.8 The initial internal composition of the Moon formed by the crystallization of the LMOThe initial depth of the LMO is 1400km, and the initial composition is the LPUM component

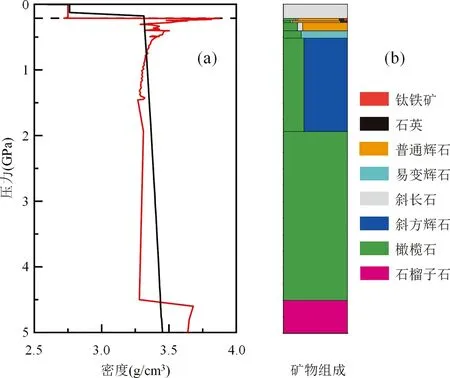
图9 月球初始内部密度和矿物组成(a)月球初始内部密度；(b)月球初始内部矿物组成. 岩浆洋初始成分为LPUM组分，深度为1400km. 红线代表计算的月球初始内部结构，黑线代表月震数据约束的目前月球密度曲线(Garcia et al., 2011)，黑色虚线代表月壳底部界面Fig.9 The initial density and mineral constitution of the lunar interior(a) initial lunar interior density; (b) initial lunar interior mineral composition. The initial composition of the LMO is the LPUM component, and the initial depth is 1400km. The red line represents the calculated initial lunar internal structure, the black line represents the current lunar density profile constrained by the lunar seismic data (Garcia et al., 2011), and the black dashed line represents the bottom interface of the lunar crust

模拟结果显示，在岩浆洋早期的平衡结晶阶段将会结晶出2.5%的石榴子石，尽管针对石榴子石在岩浆洋早期的结晶方式尚不明确，但其密度大于橄榄石，因此本文假设石榴子石完全与熔体分离并堆积在岩浆洋底部。由于石榴子石的结晶，在岩浆洋底部会存在一个相对富Al、Ti、Ca和Cr的储库。橄榄石在平衡结晶阶段结束后堆积在石榴子石之上，这一阶段的橄榄石成分变化不大，Mg#从95逐渐降低到94，基本不含Ti、Al和Cr元素。岩浆洋结晶到400km后(对应压力为2.0GPa)，斜方辉石开始结晶，由于辉石与橄榄石之间的成分差异，并且不同阶段橄榄石和辉石的结晶比例不同，月幔的SiO2和MgO含量发生波动。在结晶程度达到78%后斜长石开始结晶，岩浆洋的Al2O3被大量消耗，并且斜长石开始上浮，只有少部分留在月幔中。与此同时，低钙的易变辉石取代斜方辉石结晶，并在结晶程度达到85%后被高钙的普通辉石取代，普通辉石的结晶导致月幔中CaO含量明显增加。岩浆洋结晶后期，钛铁矿的结晶增加了月幔的FeO和TiO2含量，而MnO和Cr2O3含量的增加主要与橄榄石和辉石有关。

对于月壳的成分，如果认为斜长石月壳结晶时间越早越靠近月球表面的话，则在初始月壳表面，斜长石更接近纯钙长石端元，斜长石的An值(CaO/(CaO+Na2O+K2O)的摩尔比)=95,但随着岩浆洋的结晶，初始月壳最底部的斜长石An值下降至81。在月壳的底部还会出现石英，但由于石英相体积分数太低(千分之几)，其对月壳的SiO2含量影响有限。初始月壳成分中几乎不含MnO、TiO2和Cr2O3组分，并且斜长石的结晶上浮使得绝大部分铝(～64%)富集在月壳中。

月球内部初始的平均密度与结晶矿物相及其成分密切相关(图9a, b)。随着岩浆洋结晶的进行，主要矿物中铁含量随之增加(Mg#减少)，堆积物的密度也逐渐增加。辉石开始结晶后，由于其与橄榄石的密度存在差异，月球内部的平均密度略有下降，但随着辉石铁含量的增加，整体的平均密度仍在逐渐增加。由于假设10%的斜长石未能上浮，因此在斜长石加入结晶序列后，月球内部的平均密度随斜长石的结晶比例而出现波动。岩浆洋结晶程度达到97%后，钛铁矿的结晶使得后期堆积物的平均密度增加到3.8g/cm3左右，结晶的含钛铁堆积物厚度约为17km。钛铁矿的结晶可能导致后期含钛铁矿层由于重力不稳定而发生翻转到月幔深部，引发后续月球更复杂的演化过程(Elkins-Tantonetal., 2002)。图9a同样展示了由Garciaetal.(2011)根据月震数据约束的现今的月球内部平均密度，由于钛铁矿和石榴子石的结晶，本文计算结果的初始月幔浅部和最深部的密度均大于现今根据月震数据推测值，而在月幔其它区域则大于本文模拟的初始月球密度结构。本文通过对两条密度曲线在每1vol%月幔中的差异进行了计算，总体的差异为0.036g/cm3，相对差异在1%左右，暗示了后期月幔翻转导致月幔的密度发生变化，最终接近如图9a黑色曲线所示的现今月球内部密度分布情况。

含钛铁矿层翻转能否发生的关键参数在于其与下伏月幔的粘度对比，当粘度比值至少达到10-3以上时才可以完全翻转到月幔深部(Elkins-Tantonetal., 2002; Lietal., 2019; Yuetal., 2019)。同时，含钛铁矿层的厚度也影响着翻转的发生，本文得到的含钛铁矿层厚度为17km，这要求含钛铁矿层与下伏月幔的粘度差异更大(Lietal., 2019)。本文的模拟结果显示月球深部存在石榴子石，而石榴子石的粘度在无水条件下远高于橄榄石(Katayama and Karato, 2008)。如果认为月球内部的水含量在10μg.g-1以内(Huetal., 2021)，石榴子石相对橄榄石的粘度比值将超过102，因此含钛铁矿层与由石榴子石组成的月幔深部间的粘度比值可能达到10-5，也将更有利于含钛铁矿层翻转到月球核幔边界。

4 结论

通过热力学计算模拟的方法模拟月球岩浆洋的演化过程，对认识月球及其它类地天体岩浆洋的演化有很大帮助。本文借助FXMOTR程序对不同参数条件下的岩浆洋结晶过程进行了模拟计算，量化了月球岩浆洋的初始成分和深度对月壳厚度的影响；对该程序包进行了优化，使其可以在固定压力下进行结晶计算，探讨了高压条件下石榴子石结晶的情况；结合微量元素在不同矿物和熔体之间分配的理论模型，计算了岩浆洋结晶的残留熔体中的微量元素含量变化。

本文通过对不同初始物质组成和不同熔融深度的月球岩浆洋进行详细的结晶过程模拟计算后发现：

(1)不同初始成分的月球岩浆洋结晶的矿物序列大致相同，但是，初始物质组成中的CaO/Al2O3含量比值及Na2O和K2O元素的含量对斜长石和单斜辉石的结晶顺序有影响。

(2)岩浆洋结晶形成的初始月壳厚度主要受月球初始物质组成中Al2O3含量和岩浆洋深度的影响，但是初始物质组成中的其它元素如TiO2、Na2O和K2O等也会影响斜长石的结晶从而影响月壳厚度；

(3)如果岩浆洋初始深度接近核幔边界，LPUM组分的月球岩浆洋深部将结晶2.5%的石榴子石，90%斜长石上浮形成月壳，可满足最新的GRAIL探测数据对月壳厚度的约束；并且结晶分异最后阶段的残留熔体的主微量元素含量也与urKREEP类似。

(4)通过详细计算月球岩浆洋结晶分异过程，建立了月球初始的结构模型，并将初始密度结构与目前月球密度结构的差异进行了计算。结果显示月球岩浆洋演化后期的月幔翻转可以消除月幔深部和浅部的密度差异，使月球内部的密度接近月震推测值，而一个由石榴子石组成的月幔最深部将有利于含钛铁矿层翻转到月球核幔边界。

目前对于高压条件下，不同岩浆洋成分结晶石榴子石的实验仍然很匮乏。因此，本文探讨的月幔深部含石榴子石的模拟结果仍需要进行相关的高温高压实验对其进行验证，特别要关注石榴子石在高压下的结晶顺序、具体成分及含量。

致谢感谢Longhi和Davenport所建立的热力学模拟程序以及中国科学院地球化学研究所杨晶助理研究员在月球岩浆洋演化研究方面的帮助。两位匿名审稿人对本文提出了宝贵的修改意见和建议，在此深表感谢。感谢俞良军副主编在完成本文方面的辛勤工作。