基于高阶统计量的心音特征提取与分类研究

朱燕琼，潘家华，杨宏波，王威廉

(1. 云南大学信息学院，云南 昆明 650091；2. 云南省阜外心血管病医院，云南 昆明 650102)

1 引言

心音信号是人体重要的生理信号[1]，它反映心脏及心血管系统机械运动状况，含有心脏各部分及相互间作用的生理、病理信息[2]。心脏听诊是先天性心脏病(简称先心病)初诊的主要手段，但需要医生具有丰富的临床经验，这一过程具有一定的主观性，缺乏客观标准。高阶统计量已经在其它生理信号的分析研究方面取得良好效果，ARMA(autoregressive moving average)模型广泛用于对随机信号的参数估计。本文采用高阶统计量并结合ARMA模型对心音信号通过数字化分析手段，提取心音信号的特征进行分类，以达到机器辅助诊断的目的。

近年来对心音信号的研究，备受国内外学者的关注，心音信号预处理通常包括：去噪、提取包络、分段定位，以及特征提取等[3，4]。国内利用高阶统计量分析心音信号一般采用AR模型或MA模型进行参数估计[5]，国外对心音信号分析研究较国内早，L.Durand在1986年将传统谱分析和现代谱分析方法应用于植入主动脉位置上的人工生物瓣膜音的分析，并将两种谱分析的性能进行了比较[6]，Moukadem Ali运用高阶统计量和时频域特征对心脏压力测试下心音的分类[7]，对严重的心动过速和快速性心律失常时，提取其心音的S1、S2的特征进行分析，但利用高阶统计量ARMA模型分析心音信号尚未见报道。本研究对采集到的心音信号直接用高阶统计量的ARMA模型和梅尔对数系数[8](MFSC)进行特征提取，并用三种K近邻，决策树，贝叶斯分类器进行分类研究和比较。

2 高阶统计量的ARMA模型提取特征

2.1 高阶统计量

高阶统计量(high-order satistics，简称HOS)是指阶数大于二阶的统计量，如高阶矩、高阶累积量、高阶矩谱，以及高阶累积量谱。这些统计量对非高斯性、非最小相位、有色噪声或非线性等必须考虑的问题有着特殊作用，能揭示常规功率谱分析所不能表现得重要信息[9]。对于高斯的信号，其高阶累积量为0，因而可有效抑制高斯有色噪声。心音信号也是一种非高斯、非线性、非平稳的生理信号，传统时频域分析难以准确表征信号特征。高阶统计量已在脑电信号、心电信号、肌电等生理信号分析上取得好的效果[10]，还广泛应用于各个实际信号处理领域。例如，通信、声纳、雷达、生物工程、语音处理、地震信号处理、图象处理、时延估计、系统辩识、自适应滤波以及阵列处理等领域都得到广泛应用[9]。

r阶矩和r阶累积量的一般表达式，分别表示为式(1)、(2)

mk=mk1 k2…kn=mom(x1，x2，…，xk)

(1)

ck=ck1 k2…kn=cum(x1，x2，…，xk)

(2)

对随机过程{x(n)}，根据高阶累积量定义式(2)可知，{x(n)}的各阶累积量为

C1x=E{x(n)}=0

(3)

C2x(τ)=E{x(n)x(n+τ)}=r(τ)

(4)

Ckx(τ1，τ2，…τn-1)=0，k≥3

(5)

由高阶矩定义式(1)可推知，只有奇数阶的高阶矩才等于零，而偶数阶的高阶矩不等于零，即

(6)

高阶统计量中，最简单、最常用的是三阶累积量和三阶谱(又称双谱)，设高阶累积量Ckx(τ1，τ2，…τn-1)绝对可和，即

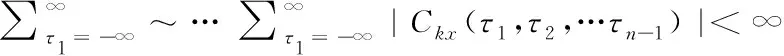
(7)

则随机信号{x(n)}的k阶累积量谱Cnx(ω1，ω2，…，ωn-1)存在并连续，且定义为k阶累积量的(k-1)维Fourier变换，即

Skx(ω1，ω2，…，ωn-1)=

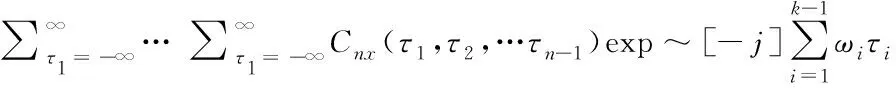
(8)

式中k=3≤π，|ω2|≤π，|ω1+ω2|≤π。

据以上分析，本研究将高阶统计量应用到心音信号的分析中，利用高阶累积量抑制高斯有色噪声，目的在于提取更能反映心音本质的特征，获取更有效的分析结果。高阶累积量具有相关函数无法比拟的优点，能够用来辨识非最小相位系统。

2.2 ARMA模型

心音信号被认为是一种随机时间序列，为随机信号建立参数模型是研究随机信号的一种基本方法，ARMA模型是研究时间序列的重要方法，在自然科学和经济学中得到了广泛的应用。ARMA模型由自回归模型与移动平均模型为基础，是现代谱估计中的参数谱估计[11]。功率谱估计是数字信号处理的重要内容和重要应用点之一，主要研究信号在频域中的各种特征，在有限数据中提取淹没在噪声中的有用信号。信号功率谱一般可以分为平谱、线谱和ARMA谱3种。平谱是白噪声谱，线谱是一个或多个正弦信号功率谱，ARMA谱介于平谱和线谱两种谱之间，是一个零极点模型，既有峰值又有谷点的谱，而AR模型则仅易于反映谱中的峰值，MA仅易于反映谱中的谷点。根据以上分析采用ARMA模型分析和计算心音信号的特征值。综上所述，将高阶统计量ARMA模型用于心音信号分析的优点：

1)高阶统计量ARMA模型不仅保留心音信号幅度信息，同时也保留了相位信息；

2)高阶统计量ARMA模型具有更好的抗噪性，根据式(2)、(5)高斯信号的高阶累积量C3，X(τ1，τ2)=0为，理论上能够抑制高斯噪声的影响，改善信噪比；

在观测数据较短的情况下，要获得高分辨率的双谱估计，必须使用参数化双谱估计方法，非参数化多谱估计是低分辨率的[15]。因此本实验采用ARMA参数模型法对心音信号进行双谱分析。设序列x(n)满足三阶平稳，由式(3)给出ARMA(p，q)模型：

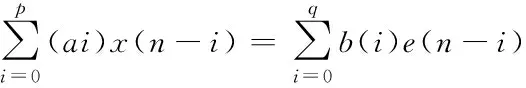
(9)

式中e(n)是具有有限的非零累积量的高阶白噪声。

2.3 心音信号提取特征

在matlab高阶统计量工具箱中，q-slice(对角切片)又称切片双谱或1.5维谱，可以去除非线性耦合，而且具有抑制噪声的能力。 残差(residual)是模型的拟合值(fitted value)与实际观测值之差。实验中调用高阶统计量工具箱中armaqs函数使用q-slice算法，调用armarts函数使用残差时间序列估计ARAM模型参数，函数中的p和q个分量组成了心音信号的特征向量，经实验对比，选取MA阶数(函数中q)为5，AR阶数(函数中p)为6时，累积量阶数取默认值3，累积量的最大滞后数目为11，FFT的计算长度为256，在二维FFT中，f1和f2分别是FFT矩阵行和列相关的频率向量，此时由频率向量，相位对角切片分量和ARMA参数向量组成特征向量，参数个数为1046。预处理的部分分析图如图1-图6所示。

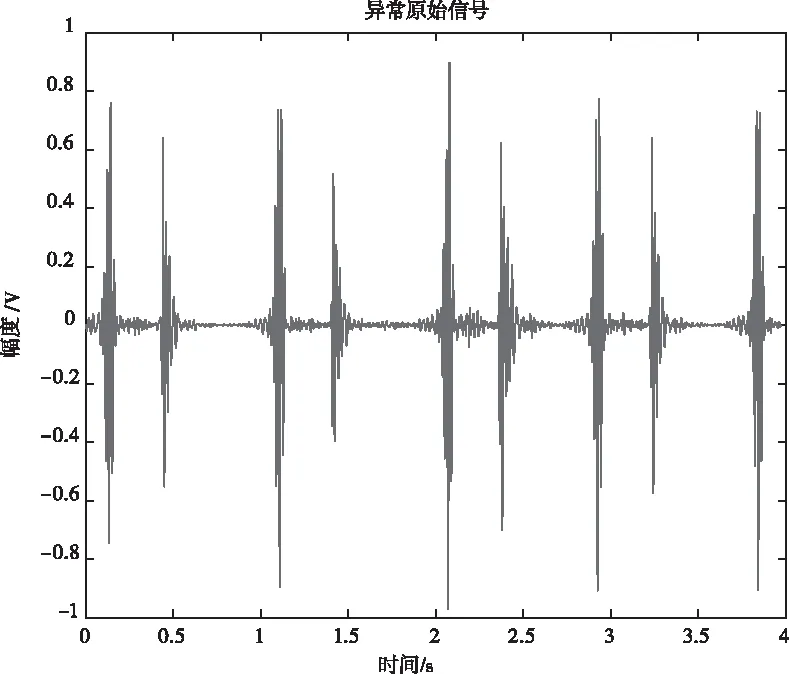
图1 房间隔缺损心音原信号

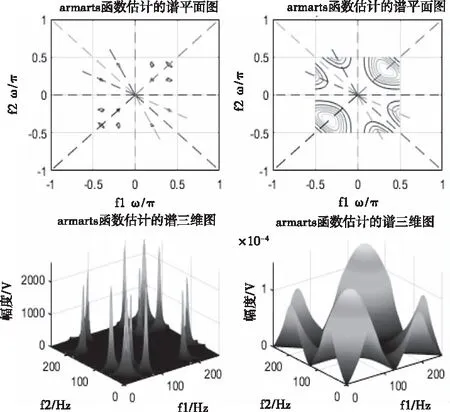
图2 房间隔缺损信号的高阶谱平面图和三维图

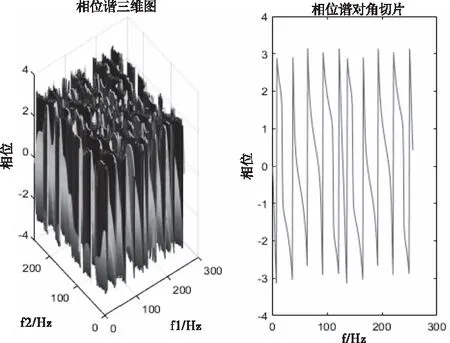
图3 室缺信号的相位谱 三维图和相位谱对角切片图

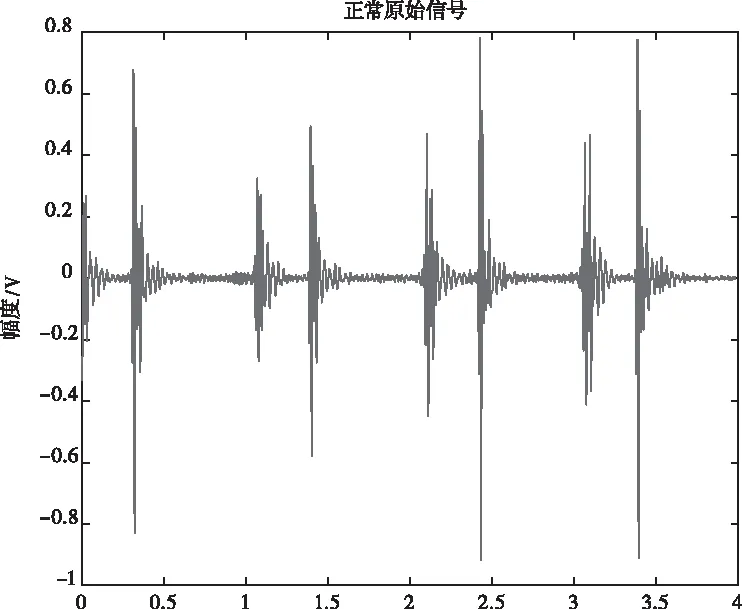
图4 正常心音原信号

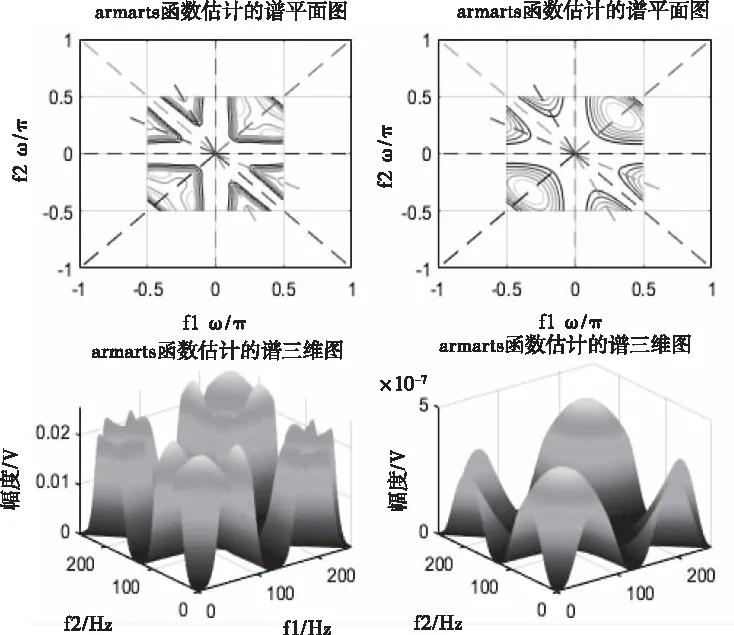
图5 正常信号的高阶谱平面图和三维图

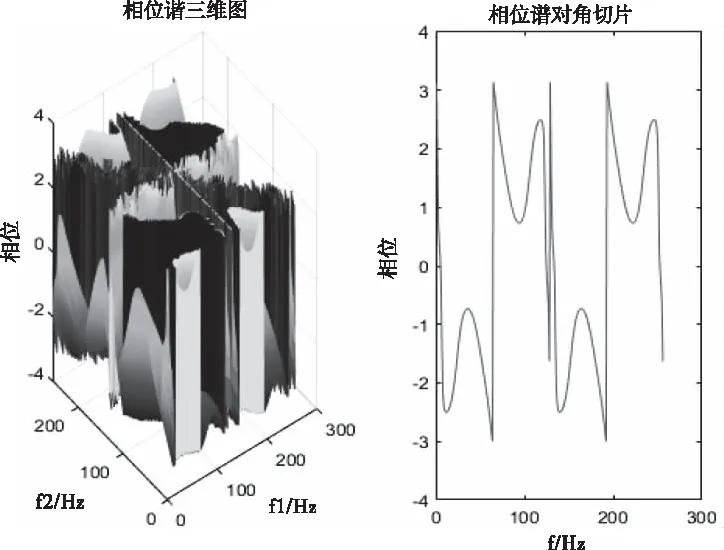
图6 正常信号的相位谱 三维图和相位谱对角切片图

图2、图3、图5、图6是特征提取过程中，原始房间隔缺损心音信号和正常心音信号及对应高阶统计量谱图。心动周期中，因血流冲击心室壁和大动脉等因素引起机械振动，产生心音。受环境噪声、呼吸音等影响，从时域直接观察4秒的异常心音信号和正常心音信号区别微小，但是观察其对应高阶统计量谱图2和图5，可以发现异常心音信号高阶统计量谱图2比正常心音信号高阶统计量谱图5中高频成分要多，异常心音信号幅度数量级是10-4，正常心音信号幅度数量级是10-7。从相位三维图3和对角切片图6可以看出，室缺心音信号相位波动大，且相位起点更多从负相位到正相位。可见采用高阶统计量易于对正常和异常心音进行区别性研究和分析，并提取更有效的特征。

3 梅尔频率系数

MFCC中的梅尔刻度是一种基于人耳对等距的高音变化的感官判断而制定的非线性频率刻度，能较好地反映人耳对声音的特点[12]。MFSC是省略离散余弦变换步骤的MFCC的特殊形式，直接对梅尔频率系数取对数能量。MFSC相比较MFCC光谱能量能保持局部特性，在频谱上更为平滑[13]。

人耳对声音的感知是非线性的，以取对数的方式可以更好的描述。分帧只能反映本帧的心音信号特性，差分更能体现心音信号时域连续性，即常用一阶差分(Δ)和二阶差分(Δ-Δ)实现，如式(10)(11)所示。把得到的mfcc参数，一阶差分，二阶差分组成一维度矩阵，即M=帧数190*3，经过34(符号表示为N)个滤波器，即得到M×N的二维特征，在保证特征参数完整的前提下，将570*34(在这里M=570为移动的帧数，34为滤波器个数)二维的矩阵，按每阶滤波器依次存放转化为一维数据。最终得到19380个参数。

Δ=y(x+1)-y(x)

(10)

Δ-Δ=y(x+2)-2y(x+1)+y(x)

(11)

式中x为自变量。Δ是一阶差分，Δ-Δ是二阶差分。

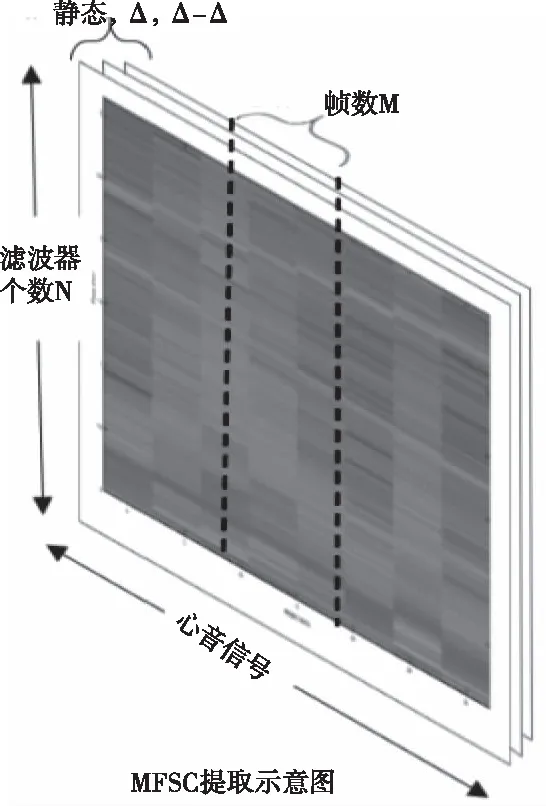
图7 心音信号的MFSC数据组织

MFSC处理的基本步骤：

1)预加重。将信号x(n)通过一个高通滤波器，其目的是补偿高频部分，突显高频的共振峰。

2)分帧、加窗。分帧是短时非平稳的心音信号近似为平稳信号，加窗可以克服频谱泄露现象。分帧时信号交叠一般为50%，以提高时间分辨率。分帧的帧数M计算如式(12)所示

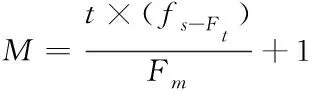
(12)

3)频域变换。信号在时域上很难观察其能量特性，通常把它转换成频域上的能量分布，能量分布来代表心音信号的特性。本文使用傅里叶变换，其计算公式如式(13)所示：

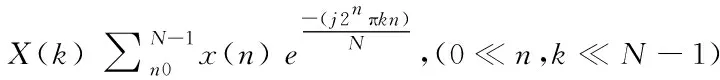
(13)

4)梅尔刻度转换。由于频域信号有很多冗余，梅尔滤波器组可以对频域进行精简，一个滤波器产生一个频段值，每一个频段用一个值表示。

5)能量取对数、差分。

4 分类识别模型

4.1 KNN

k近邻(kNN，k-NearestNeighbor)是实践中最成功的算法之一，它在理解、实践上较简单，但产生了令人难以置信的良好结果。它是一种通用分类器，在蛋白质分类，计算机视觉，计算几何和图形等方面都有应用。KNN是基于实例的学习(也称为惰性学习)，其中函数仅是局部近似的，所有计算都会延迟到分类为止。在KNN中，给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息进行预测。任何给定实例均按其“ k”个最接近的邻居按多数票进行分类，其中“ k”是一个重要参数，是正整数，通常很小，当k取不同值时，分类结果会有显著不同。给定测试样本x，若其最近邻样本为z，则最近邻分类器出错的概率就是x与z类别标记不同的概率[14]，如式(14)所示

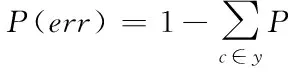
(14)

4.2 决策树

决策树是一种树形结构的分类器，通过顺序询问分类点的属性决定分类点最终的类别。本文根据心音信号的MFSC特征和高阶谱特征，构建一颗决策树。分类是按照结点依次进行判断，即可得到样本所属类别。随着划分过程不断进行，希望决策树的分支结点所包含的样本尽可能属于同一类别。即结点的“纯度越高”， “信息熵”是度量样本集和纯度最常用的一种指标[14]。假定当前样本集D中第k类样本所占的比例为pk(k=1，2，…，|y|)，则D的信息熵定义如式(15)所示

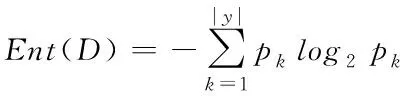
(15)

4.3 朴素贝叶斯

朴素贝叶斯分类器是一个以贝叶斯定理为基础的多分类的分类器。对于给定数据，首先基于特征的条件独立性假设，学习输入输出的联合概率分布，然后基于此模型，对给定的输入，利用贝叶斯定理求出后验概率最大的输出，如式(16)。

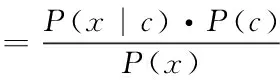
(16)

式中P(c)是类先验概率，P(c│x)是样本x相对于类标记c的类条件概率或称“似然”。

5 实验设计与评估标准

5.1 实验设计

本节重点对比讨论本文的高阶统计量特征提取和梅尔倒谱系数特征提取算法，主要研究内容是在matalb和tensorflow平台上实现。研究所用的数据源为，从云南省阜外心血管病医院临床从和全国各地先心病筛查采集的心音信号，实验取其中1000个心音样本，800用于训练，其中正常心音样本600个，先心病心音样本200个 ；200个样本进行对比测试，该测试集中有正常心音样本100个，先心病心音样本100个。实验心音信号时长为20s，采样率为5kHz。

5.2 评估标准

二分类算法常采用灵敏度(符号记为：se)、特异度(符号记为：sp)和准确率(符号记为：acc)作为算法评价指标。根据金标准准则，表示正确分类的异常信号为真阳性(符号记为：TP)；错误分类的异常信号为假阳性(符号记为：FP)；表示正确分类的正常信号为真阴性(符号记为：TN)；表示错误分类的正常信号为假阴性(符号记为：FN)，灵敏度、特异度和准确率计算如式17‐式19所示。

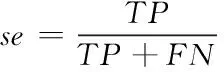
(17)

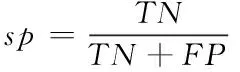
(18)

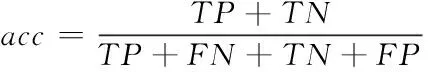
(19)

6 实验结果与分析讨论

6.1 实验结果

实验中所用的1000例心音数据均来自经临床确诊的心音信号，其中训练集800例，测试集200例。利用高阶统计量的ARMA模型直接提取先心病心音信号的特征，用K近邻，决策树，贝叶斯分类器对其进行分类识别，并与用梅尔对数系数提取特征的方法进行了对比，结果如表1所示。从数据库中随机选取正常和异常各200列原始信号进行t检验，结果P<0.01，表明正常和异常数据具有显著性差异。

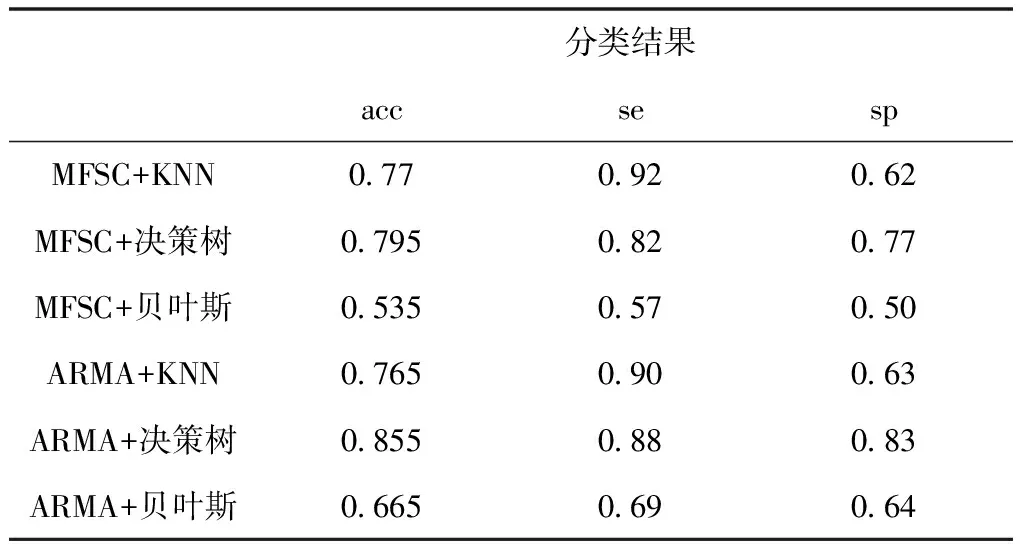
表1 各类算法的比较

表中，分类结果sp为特异度，se为灵敏度，acc为准确率。

6.2 分析讨论

从实验结果可以看出K邻近，决策树，贝叶斯三种机器学习分类模型效果的差异性，贝叶斯分类在MFSC和高阶统计量中均不理想， KNN没有决策树分类结果好，原因是本实验中对于MFSC的特征来说k取值小了，但为保证实验结果的可比性，k值根据训练集综合考虑决定。决策树更适宜于这两种特征提取后心音病例的分类，针对未去噪截取的原始心音信号，与MFSC相比高阶统计量ARMA模型总体效果好。

7 结论

本文提出基于高阶统计ARMA模型直接提取心音特征，省去了一般预处理中，对心音的降噪和分段定位过程，提高了分析效率，降低了特征参数数量，加快了运算速度。运用KNN，决策树和贝叶斯三种不同的分类器进行分类判别评测，发现决策树更适合ARMA和MFSC这两种特征提取后心音病例的分类。实验发现高阶统计量ARMA模型与梅尔对数倒谱(MFSC)相比，针对未经过去噪，分段定位的原始心音信号，高阶统计量ARMA模型在测试集上更有竞争力，计算速度更快。此方法预处理方法简便，为机器辅助诊断和远程听诊提供一种好的选择。