基于光栅传感的剪力墙结构抗侧刚度检测仿真

乔俊飞，闫永利

(内蒙古农业大学建筑工程技术系，内蒙古 呼和浩特 014100)

1 引言

剪力墙结构[1]凭借抗侧刚度大与布置灵活等优势，在住宅、写字楼等高层建筑中得以广泛应用。此类结构的受力机制与变形特征不同于其它墙体，因其多数地震侧向力均被较大的抗侧刚度所承担，导致剪力墙更易较早地进入塑性阶段。抗侧刚度[2]是墙体进行力学分析的重要弹性参数之一，特别是在遇到强震后，剪力墙结构在发生塑性变形的同时，抗侧刚度会大幅下降，影响建筑整体抗震性能，因此，对其展开深入研究具有重要的意义。

文献[3]面向低屈服点钢板剪力墙，基于内填钢板的附加作用，探讨其在水平荷载作用下的抗侧刚度与抗剪承载力；文献[4]采用ABAQUS有限元分析软件，模拟计算基础隔震双肢剪力墙结构，分析其抗侧刚度在隔震支座竖向变形阶段所受到的影响。

鉴于抗侧刚度在建筑结构中的重要程度，为更好地优化剪力墙结构设计、探讨抗侧刚度影响，本文利用光栅传感技术，完成剪力墙结构的抗侧刚度检测。该方法的主要创新点为：

1)采用光栅传感技术实时监测相关信号，可以满足抗侧刚度的即时性检测需求；

2)通过敏感元件与转换元件可以提升检测技术的精密性，有利于提升检测结果的准确性，有效降低了监测误差；

3)凭借中心波长变化量与周期、有效折射率之间的关系，使本文方法能够应用于大部分与这两个物理量有关的相关检测。

4)光栅振动传感器根据中心波长在剪力墙中所形成的位移量检测出抗侧刚度，能够有效抑制抗侧刚度影响系数的干扰。

2 光栅传感技术约束条件分析

假设反射光的中心波长及其变化量分别为l、Δl，光栅有效折射率及其变化量分别为neff、Δneff，光栅调制周期及其变化量为Λ、ΔΛ，则光栅布拉格方程式及其微分表达式分别如下所示

l=2neffΛ

(1)

Δl=2ΔneffΛ+2neffΔΛ

(2)

根据光栅的微分形式可知，其中心波长变化量与周期和有效折射率有关，也就是说，但凡是具有改变调制周期与有效折射率能力的物理量，均能够根据光栅中心波长形成的位移量而完成检测。诸如应力、温度等较为直接的物理量，由于应力作用会使光栅出现伸缩变化，故经过调制光栅周期与折射率，即可改变光栅中心波长；对于温度物理量而言，如光纤中发生的热膨胀效应与热光效应等[5]，也都会直接影响光栅的周期与折射率。

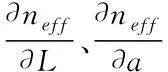
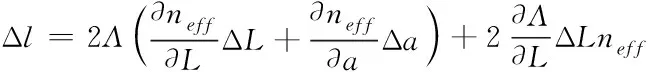
(3)

若光纤具备各向同性特征[7]，则不考虑半径对折射率的影响，因此，改写上式为如下表达式

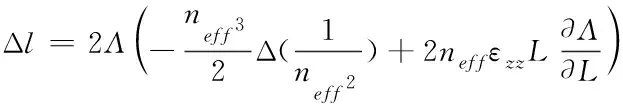
(4)

其中，εzz表示轴向应变。

结合式(3)与有效单光系数Pe，推导出轴向均匀应变情况下的光栅波长相对变化方程式，如下所示

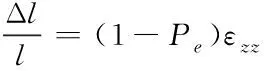
(5)

光栅传输光波阶段，光栅折射率会发生改变，各模式之间的正交状态也会随之改变，故当不同模式间产生相互耦合现象时，慢电场振幅需满足一定条件[8]。

假设理想条件下的光栅折射率可通过下式解得

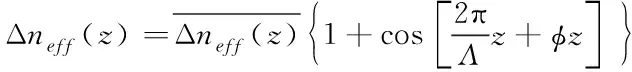
(6)

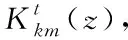
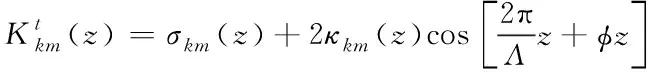
(7)

因此，若正、负方向传播的电场模式分别是Af(z)、Ab(z)，则传播方向为光纤正方向与负方向的慢电场m振幅Am(z)、Bm(z)，需满足下列约束条件

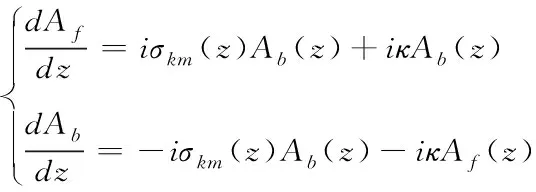
(8)

3 面向剪力墙结构抗侧刚度的光栅振动传感检测

基于光栅传感技术，创建一个图1所示的光栅振动传感器，根据墙体的惯性特点，将其a表面固定在待测的剪力墙上，并通过位移、速度以及加速度等物理指标来描述剪力墙抗侧刚度的惯性振动。

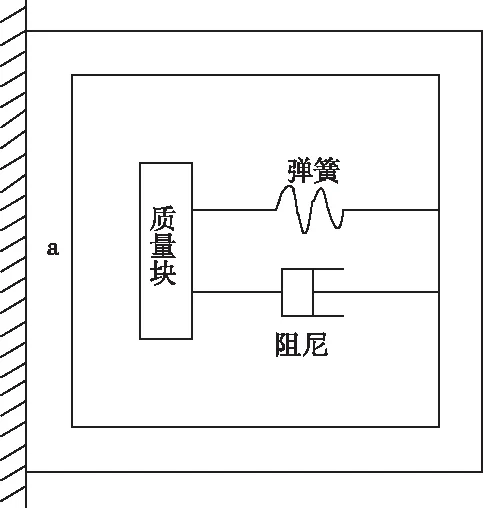
图1 光栅振动传感器

假设图1中光栅振动传感器的质量块质量是M，弹簧弹性系数是K，阻尼器阻尼是C，当质量块发生y位移量时，墙体将带动传感器发生x位移量，可用正弦信号Xsinωt表示，其中，X是输入信号位移，ω是墙体的待测角频率，t是信号周期，故基于牛顿第二定律[9]，推导出下列质量块M的动力学方程式

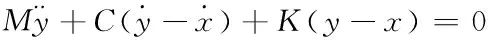
(9)

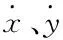
令质量块与剪力墙体间的相对位移量是z=y-x，则将上式改写成如下表达式

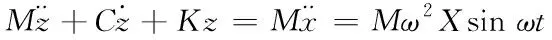
(10)

若相对位移量z是上列方程的特值，且满足z=Zsin(ωt-φ)，其中，Z是输出信号位移，φ是信号初始相位，余弦信号形式为Zcos(ωt-φ)，则代入上式后即可得到下列合并式

(K-Mω2)Zsin(ωt-φ)+CωZcos(ωt-φ)=Mω2Xsin(ωt)

(11)

按照ωt-φ与φ的形式展开等式右侧，因上式恒成立，故有下列方程组

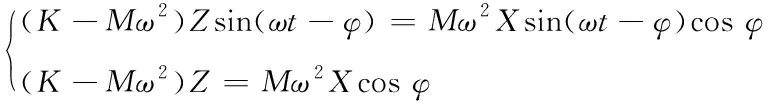
(12)

整理该方程组后得到下列简化等式组

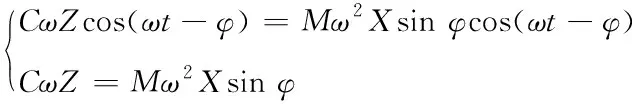
(13)

根据三角函数相关定理，改写上式为如下表达式

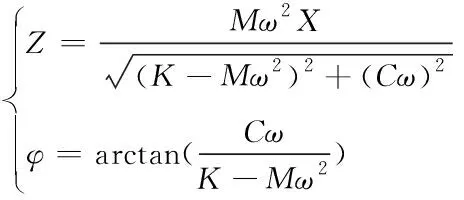
(14)

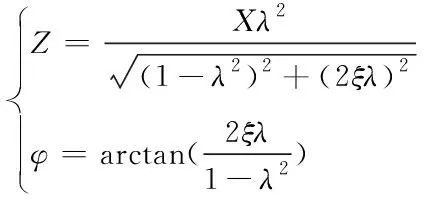
(15)

由此推导出振动传感器放大系数β的计算公式，如下所示

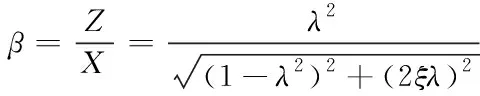
(16)

剪力墙抗侧刚度的光栅传感检测关键点是输入信号能够不失真地反复出现。不失真检测阶段存在两种情况：

1)当输入、输出信号的商结果是常数，初始振幅为A0时，有z(t)=A0x(t)；

2)当输入、输出有商结果，且输出比输入略有滞后时，有z(t)=A0x(t-t0)。其中，t0表示初始的信号周期。

采用拉普拉斯变换法处理输入、输出信号之间的关系条件，得到自变量jω的傅里叶变换方程组，如下所示，其中，e*表示欧拉函数

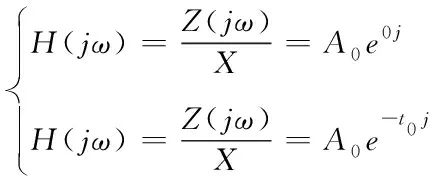
(17)

从该式可以看出，检测抗侧刚度过程中的不失真幅频特性与相频特性，可通过下列等式组合解得

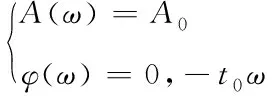
(18)

若待测角频率与固有角频率的比值λ趋近于无穷大，则将放大系数计算式(16)改写成下列表达式

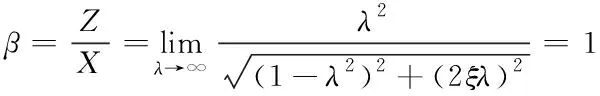
(19)

由放大系数达到1可知，检测阶段的不失真需求得以满足。当传感器固有频率ωn值较小并符合ωn≪ω时，Z≈X，这说明在反应输入位移X时，输出位移Z具备不失真能力，故基于此来检测出剪力墙的抗侧刚度振动位移。

若待测角频率与固有角频率的比值λ趋近于0，为使方法适用于抗侧刚度检测，需将(16)改写成下列表达式

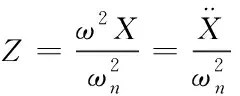
(20)

由该式可以看出，输出位移Z随的增加而上升。当传感器固有频率ωn的值较大且远超出待测角频率ω时，振动传感器能够不失真地检测出抗侧刚度的加速度。

4 剪力墙结构抗侧刚度检测仿真

4.1 仿真前期准备

采用ANSYS软件建立一个剪力墙结构建筑，编号20个传感器后，将其均匀地分布于6米、8米剪力墙等位置上，如图2所示。在实际的现场应用中，需把选取的埋入式光栅传感器铺设在建筑中，因混凝土浇筑完成后就无法更换传感器，所以，要提前记录并测试好设备是否能够精准、正常运行，待安装完所有传感器后，依据剪力墙工况，按照固定周期采集传感器数据，以便于后期对比分析。

图2 剪力墙传感器分布图

4.2 抗侧刚度检测性能影响因素研究

为验证本文方法的切实可行性，采用Origin软件模拟、分析在单调水平荷载作用下，剪力墙抗侧刚度的肋格宽度、肋格密集程度以及刚度影响系数对检测效果的影响，检验本文方法对影响因素的免疫性。基于建筑抗震试验方法规程，利用割线刚度表示结构的抗侧刚度实际结果，将其与检测结果对比，验证方法的精准性。其中，割线刚度的计算公式如下所示，第i次峰值点的正向荷载值与位移值是+Fi、+Xi，负向荷载值与位移值是-Fi、-Xi：

(21)

4.2.1 肋格宽度与检测性能相关性

图3所示为2肋梁3肋柱与3肋梁3肋柱下不同肋格宽度的实际抗侧刚度结果与检测结果。由此可以看出：剪力墙抗侧刚度值随着肋格宽度的增加而上升，且增幅也随之呈一定比例不断增加。这是因为混凝土砌块的约束作用受到了肋格宽度的强化，从整体上增强了剪力墙的结构性能，使抗侧刚度得以提高。本文方法因采用融合了光栅传感技术的振动传感器，故检测结果与实际的抗侧刚度值拟合度较高，受肋格宽度因素影响较小。

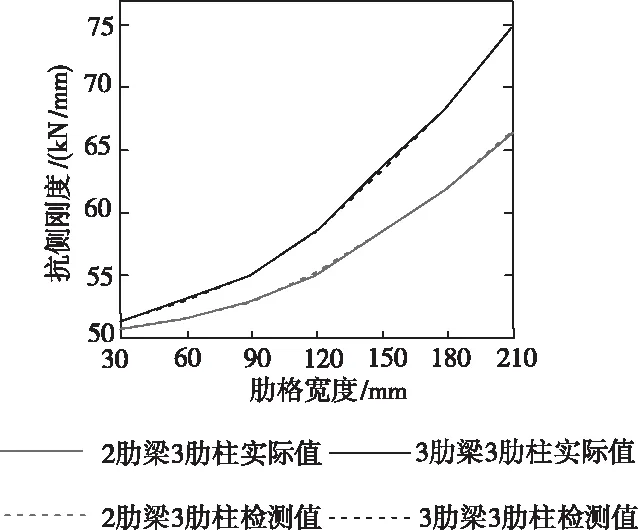
图3 肋格宽度对抗侧刚度实际值与检测值的影响

4.2.2 肋格密集程度与检测性能相关性

图4所示为肋格宽度为120mm时，2肋梁与3肋梁下不同肋柱数量的实际抗侧刚度结果与检测结果，由此可以看出：剪力墙抗侧刚度值与肋格密集程度之间呈正相关关系，这是因为较高的肋格密度约束、支撑了混凝土砌块，增强了对砌块裂缝的控制能力；随着肋柱数量增加，尽管抗侧刚度值有所上升，但增幅始终相对较小，说明肋格密集程度对剪力墙结构的抗侧刚度影响较小；通过对比抗侧刚度的实际值与检测值可知，本文方法将墙体带动传感器所发生的位移量作为检测目标，所以，具有较高的检测精准度，且几乎不受肋格密集程度的影响。

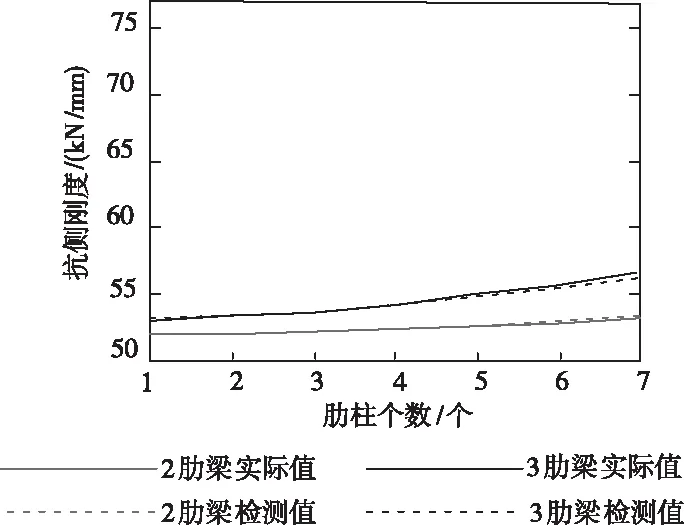
图4 肋格密集程度对抗侧刚度实际值与检测值的影响

4.2.3 抗侧刚度影响系数与检测性能相关性

在肋格宽度是120mm、肋柱数量是9根的设定条件下，模拟出抗侧刚度影响系数对2肋梁3肋柱与3肋梁3肋柱的检测影响，如图5所示。根据图中的数值分布形式可以看出：抗侧刚度值与影响系数呈显著负相关，且实际值与检测值拟合度不随影响系数变化而改变。究其原因是光栅振动传感器是根据中心波长在剪力墙中所形成的位移量而检测出抗侧刚度的，其惯性振动通过位移、速度以及加速度等物理指标完成描述，故不仅检测准确度较高，而且有效抑制了抗侧刚度影响系数的干扰。

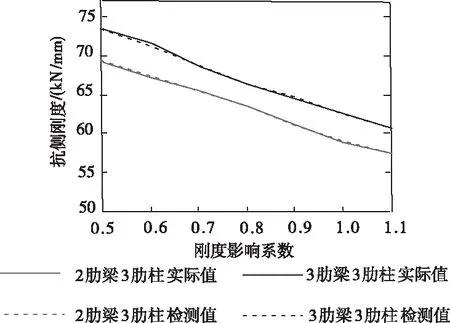
图5 刚度影响系数对抗侧刚度实际值与检测值的影响

4.3 基于肋格宽度与肋格密集程度的检测误差分析

综合肋格宽度与肋格密集程度因素，探讨不同情况下的抗侧刚度实际值与检测值误差。根据表1中不同框格形式与不同肋格宽度对应的具体数值与误差可以看出：抗侧刚度值的受影响程度符合上述实验结论；本文方法通过研究光栅传感的两种不失真检测阶段，使检测误差值即便是在肋格宽度与肋格密集程度的共同作用下，也能够一直处于理想水平。

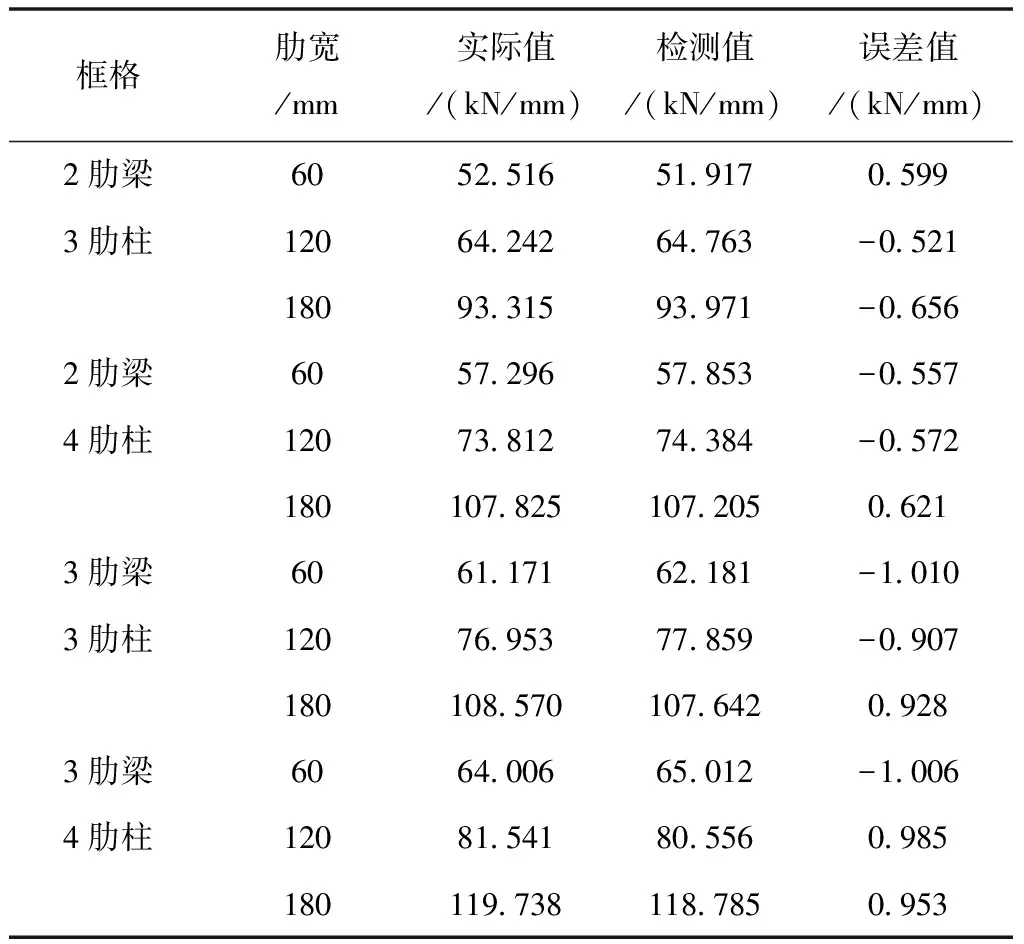
表1 肋格宽度与肋格密集程度下实际值与检测值误差

5 结论

国民经济飞速发展，大幅增加了建筑需求。在建筑承载力要求与日俱增的今天，剪力墙凭借较好的竖向荷载与水平荷载承重效果，常被用作建筑墙体的主要结构形式。该墙体结构的抗侧刚度作为承载力的主要描述指标，准确检测出其数值具有重要的现实意义与实践价值，为此，采用光栅传感技术，对剪力墙结构的抗侧刚度展开检测。下面对本文的研究成果进行如下总结：

1)考虑到中心波长变化量与周期和有效折射率有关，对光束传输过程中不同方向模之间的耦合现象进行分析，获取由墙体带动传感器所发生的位移量。

2)借助传感技术中的敏感元件与转换元件提升检测技术的精密性，提高了检测结果的准确性。

3)实验结果表明：肋格宽度为120mm时，2肋梁与3肋梁下不同肋柱数量的实际抗侧刚度结果与检测结果；所提方法有效抑制了抗侧刚度影响系数的干扰，提高了检测精度。