基于神经网络和路侧单元指纹的车辆定位方法

张月霞，刘 冲

(1. 北京信息科技大学信息与通信工程学院，北京 100101；2. 北京信息科技大学现代测控技术教育部重点实验室，北京 100101；3. 高动态导航北京市实验室，北京 100101)

1 引言

车联网是未来智能交通系统发展的必然趋。在过去的十年里，许多智能交通应用得到了飞速的发展，如辅助驾驶、自动驾驶、车辆防碰撞、高速公路监测等。然而，这些应用需要实时且精确的车辆定位技术支撑[1]。全球定位系统(GPS)是应用最广泛的技术之一，但GPS信号在隧道、高楼密集的街区、山区、立交桥下、恶劣天气等场景中由于信号受障碍物阻挡导致其定位性能大打折扣，甚至无法完成定位[2]。另一方面，基于GPS的定位方法也无法满足未来车联网应用的定位精度需求[3]。

V2X通信是未来车联网关键技术之一，其中车与基础设施(V2I)通信是V2X通信的重要组成部分，基础设置主要包括路侧单元(RSU)与基站。以RSU为例，车辆上所搭载的车载单元(OBU)通过车联网短程通信技术(DSRC)实现信息的高速率传输[4-5]。近年来，随着车联网定位技术的不断发展，基于RSU的定位技术越来受到人们的关注。文献[6]提出一种基于加权质心算法的车辆定位方法，待定位车通过对附近路侧单元和已知坐标车辆的坐标进行加权来估算自身的位置坐标，其中权值的设定综合考虑了距离及信噪比等因素；文献[7]提出了一种基于双RSU的测距方法，其首先利用无线测距技术提取车辆与各RSU间的距离，则待定位车辆可能位于以RSU坐标为圆心距离为半径的双圆交点之上，假设车辆行驶方向已知，通过RSU广播第二轮消息后判断待定位车辆位置；文献[8]利用车辆自身的移动特性与固定RSU间联立到达时间(TOA)方程，当构建方程数量达三个及以上时，通过最小二乘法对TOA方程进行解算，从而求解待定位车辆坐标；文献[9]提出了一种基于到达角度(DOA)的车辆定位方法，待定位车辆从辅助 RSU广播信息中解算出来波角度，并利用来波角度的正切值构建包含位置的方程组解算车辆坐标。

为进一步提升定位精度，本文提出一种基于神经网络和RSU指纹的车辆定位方法。该方法将车辆所行驶的路段均匀划分为若干栅格区域，在每个栅格区域处采集不同RSU的接收信号强度(RSSI)。将所采集的RSSI作为特征值、各栅格点所对应中心坐标作为目标值构建BPNN，并估算该网络的最大预测误差值。定位阶段，待定位车辆将自身接收到各RSU的RSSI输入构建好的BPNN，并以其输出坐标为圆心，BPNN的误差最大值为半径，在约束范围内进行指纹定位来确定待定位车辆的精确位置坐标。该方法适用于对车辆定位精度要求较高的应用场景及GPS定位盲区，也可与其它定位方法相结合，实现高精度融合定位。

2 定位系统

2.1 车辆定位模型

本文所利用的车辆定位模型如图1所示，在双向二车道模型中，若干RSU交替等距部属于道路两侧且位置坐标已知，RSU在其通信范围内周期性地广播包含自身标识的数据包。网络中若干车辆在服从交通规则的情况下自由行驶于道路之中。

图1 车辆定位模型

设RSU总数为N，其中第n个RSU的坐标可表示为

Rn=(xn，yn) 1≤n≤N

(1)

设车辆V0为搭载OBU的待定位车辆，其坐标可表示为(x，y)，车辆与RSU之间的通信遵循2.2节所示DSRC链路模型。

2.2 DSRC链路模型

RSU与车辆之间的DSRC链路模型可用自由空间模型进行描述，其具体表达式可通过Friis公式[6]表示

(2)

在上式中Ps、Pr分别为RSU的发射信号功率及待定位车辆的接收信号功率，λ为信号的波长，d为RSU与待定位车辆间的距离，β为系统损耗因子，Gs、Gr为天线增益，车联网环境中通常设Gs=Gr=β=1为默认值[6]，波长λ可如下表示

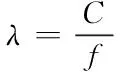
(3)

其中C是真空中光速(299，792，458m/s)，f为信号传播的频率。式(2)中功率单位为瓦特，将其进一步改写为式(4)所示dB形式[10]

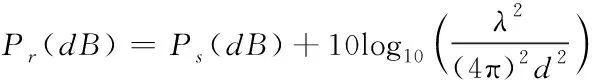
(4)

3 定位方法描述

3.1 构建RSU指纹库

将定位区域平面均匀划分为M个四边形栅格区域。在RSU指纹库的构建阶段，分别在每个栅格区域的中心处测量该位置所接收到不同RSU的RSSI并存储到数据库之中作为参考指纹点。指纹库中第m(m≤M)个参考指纹点可如下表示

Fm=(m，xm，ym，Pm1，…，PmN)

(5)

xm与ym为第m个参考指纹点的实际位置坐标，PmN为第m个参考指纹点处所接收到第N个RSU的RSSI。因此，所构建的RSU指纹库FB可如下表示

FB=(F1，F2，…FM)T

(6)

3.2 BPNN的训练

将RSU指纹库中指纹信息作为构建BPNN的训练集，用来训练神经网络。其中神经网络的特征值和目标值分别为指纹点所接收到不同RSU的RSSI和指纹点的位置坐标。本文所构建的BPNN包含输入层、隐含层及输出层。

设BPNN输入层神节点数量s0=N，在训练阶段，需将指纹库中RSSI矩阵输入网络中进行训练。设建模过程中输入矩阵为XT，可表示为

(7)

其中XM=(PM1，PM2，…，PMN)为指纹库中第M个指纹点所接收到N个RSU的RSSI向量。

设BPNN的输出层节点数量s2=2，在BPNN的训练阶段，输出层通过将XT经BPNN的所得输出值与各指纹点横纵坐标间的误差进行反向传播，对神经网络各层权值与阈值进行修正，使神经网络可以更好地拟合训练集中RSSI与位置坐标间的非线性关系，提升网络性能。

BPNN隐含层节点数数量s1可由式(8)所示经验公式求得

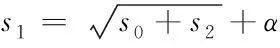
(8)

其中，s0和s2分别为输入层及输出层节点数量，α为 0～10之间的调节常数。隐含层与输出层的激励函数f1(x)和f2(x)分别选择S函数Sigmoid及线性传递函数purelin；wij与b1i分别表示神经网络中隐含层和输入层间的权值及阈值，而Wli与b2l分别表示神经网络中输出层和隐含层间的权值及阈值

因此，本文所构建的BPNN拓扑结构如图2所示。

图2 BPNN拓扑结构

由上图可知，神经网络隐含层中第i个节点的输出a1i如下所示

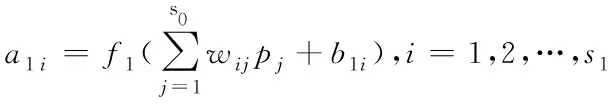
(9)

其中pj=(P1j，P2j，…，PMj)为输入层第j个节点的输入向量，输出层第l个节点的输出值a2l如下所示

(10)

性能函数为军方误差函数其定义如下

(11)

tl用来表示训练集各指纹点所对应坐标值，由于s2=2，故当l=1时，tl表示对应指纹点横坐标值；l=2时，tl表示对应指纹点纵坐标值。

在BPNN的训练过程中，若每次正向传播输出值与实际值间的的均方根误差值大于误差阀值时另该误差反向传播，并通过梯度下降法修正BPNN的权值和阈值，直到正向传播满足误差阀值要求或达到指定迭代次数后训练结束。

3.3 确定指纹匹配半径

在定位区域随机选择Q个点进行采样，用来确定后续指纹匹配算法的匹配半径，其中每个采样点表示方法同式(5)所示。

将Q个采样点对应的RSSI矩阵输入训练好的神经网络中，其中输入X′T可如下表示

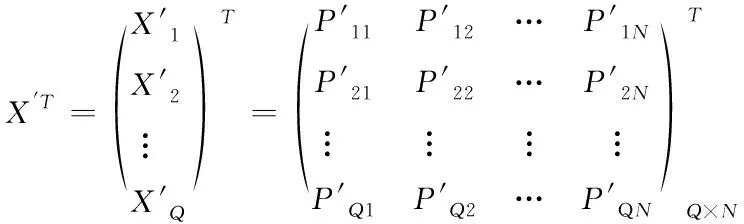
(12)

(13)

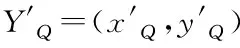
(14)

其中(xQ，yQ)为第Q个采样点的实际坐标。分别计算Q个采样点的的定位误差，并将最大误差值rmax=max{r1，r2，…，rQ}作为指纹定位的匹配半径εr。

3.4 车辆实时定位

3.4.1BPNN粗定位

定位阶段，假定待定位车辆V0所接收到各RSU的RSSI向量为

Xr=(Pr1，Pr2，…，PrN)

(15)

Yr=(xr，yr)

(16)

横坐标xr可表示为

纵坐标yr可表示为

(18)

其中wij、Wki、b1i、b2k分别为BPNN训练完成后最终的权值和阈值。

3.4.2 指纹精确定位

以神经网络的预测坐标Yr为匹配圆心，采样点最大误差值rmax为匹配半径εr，确定局部指纹匹配范围S，具体如图3所示。

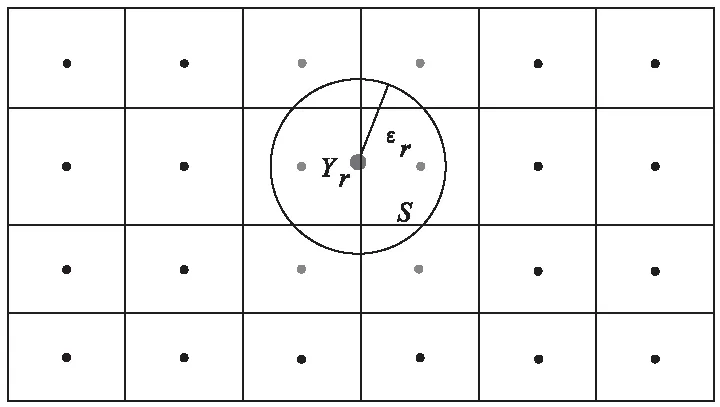
图3 局部匹配范围示意图

设局部范围S内指纹点个数为H，Rh为第h(h≤H)个指纹点接收到各RSU的RSSI向量。分别计算H个指纹点所对应RSSI向量与Xr的相似度，相似度的衡量标准是Xr与S区域内各指纹点中RSSI向量间的欧式距离，Xr与Rh间的欧式距离L2如下所示

(19)

其中，‖‖2为二范数算子，其数值越小则向量间相似度越高。将Xr与S内H个指纹点的RSSI向量进行指纹匹配，设第k(k≤H)个指纹点中的RSSI向量与Xr间具有最高匹配度，该指纹点对应的真实坐标为Tk(xk，yk)。令待定位车辆的最终位置坐标T(x，y)等于局部范围S内第k个指纹点的真实坐标，即待定位车辆最终位置坐标T(x，y)可表示为

T(x，y)=Tk(xk，yk)

(20)

4 仿真结果及分析

为验证本文所提方法性能，在MatlabR2016a中进行数值仿真。设四车道模型中单车道宽度L1=3.75m；四个RSU交替部署于道路两侧1m处，其中RSU1～RSU4的发射功率为40dB，位置坐标分别为(0，0)、(200，17)、(400，0)、(600，17)。在210～390的横坐标范围及1～15的纵坐标范围内构建大小为2700m2的定位区域，设定位区域位于四个RSU的有效通信范围内。在定位区域中均匀构建边长L2=5m的栅格区域，取每个栅格区域的重心作为参考指纹点，其中参考指纹点总数为108。默认RSU与OBU间通信距离为视距距离，记录各参考指纹点的坐标及接收RSSI值，构建RSU指纹库。RSSI值可由2.2节中DSRC信号路损模型计算求得。

设神经网络最大训练次数为1000，学习率为0.02，参数α=1。利用指纹库中数据对BPNN进行训练，并将Q=300个采样点的的RSSI值输入训练完成的BPNN，记录其输出的预测位置坐标值。通过计算Q个采样点的预测坐标与真实坐标间的差值，绘制该仿真场景下本文所构建BPNN的定位误差分布，具体如图4所示。

图4 BPNN定位误差分布图

由上图可计算求得，本文所构建BPNN的平均定位误差为3.6278m，最大定位误差rmax为6.9397m，令误差半径等于最大定位误差值，即εr=rmax。

以BPNN预测坐标为圆心，εr为误差半径，构建局部指纹匹配范围S。在S内，进一步利用指纹匹配方法求解待定位车辆的精确坐标。其中定位误差随实验次数变化折线如图5所示。

图5 本文方法定位误差折线图

由上图可计算求得本文所提车辆定位方法的平均定位误差为2.45m，与基于BPNN的车辆定位方法相比，平均定位精度提高了32.5%。为了进一步论述本文所提定位方法的定位性能，通过对比仿真，绘制本文定位方法、BPNN定位方法及无多径干扰的GPS定位方法的的累计误差分布，具体如图6所示。

图6 不同定位方法累积误差分布

从图6可看出，本文所提定位方法、BPNN定位方法、无多径GPS定位方法，定位误差小于1m的概率分别为14%、9%、9%；定位误差小于3m的概率分别为71%、29%、20%；定位误差小于5m的概率分别为100%、89%、57%。因此，本文所提车辆定位方法在定位精度方面与BPNN定位方法、无多径GPS定位方法相比具有更好的表现。

另一方面，传统指纹定位方法在指纹匹配阶段中，待定位车辆接收信号强度向量需与待定位区域内的所有指纹点进行指纹匹配，这在待定位区域范围较大即指纹点数量较多时会耗费较大的指纹匹配时间。而本文所提方法在指纹匹配阶段中，待定位车辆接收信号强度向量只需与局部范围内较少的指纹点进行指纹匹配，大大节约了指纹匹配时间，提高了定位的实时性。

5 总结

为解决车联网中常见车辆定位方法定位精度较低问题及GPS定位盲区的车辆定位问题，本文提出了一种基于神经网络和RSU指纹的车辆高精度定位方法。仿真结果表明，所提方法平均定位误差为2.45m，与基于BPNN的定位方法相比，平均定位精度提升32.5%。现阶段，车辆高精度定位问题是车联网的重要研究方向之一，其定位性能决定着车联网未来的发展与前景。而随着科技的不断发展，利用人工智能、融合定位等手段去提升车辆的定位性能也必然会成为未来车联网的重要研究方向。