势能代价PRM 算法的机械臂避障路径规划研究

张许有，刘有余*,

（1.高端装备先进感知与智能控制教育部重点实验室，安徽芜湖 241000；2.安徽工程大学 机械工程学院，安徽芜湖 241000）

路径规划算法是解决机械臂避障规划问题的核心，为此，学者们给出了如A*算法[1-2]、人工势场法[3]、强化学习法[4-5]、RRT(Rapidly exploring random tree)[6-7]、PRM[8]等，其中PRM 算法具有规划复杂度受规划空间维数和复杂度影响小的特点，对解决高自由度、强耦合的机械臂路径规划问题具有优势。

基于PRM 算法的路径规划缺点：在规划空间采点时，落于障碍间狭窄区域的节点数目少，使算法在路径搜索时，无法通过狭窄区域，导致结果大幅偏离最优路径或规划失败。最直接的解决途径是通过增加采样点，提高自由空间中采样点数目。但该方法存在两个问题：自由空间节点的增加，不能有效增加障碍间狭窄区域内的节点，使规划依旧易失败或大幅偏离最优路径；采样点的增加，提升了PRM 算法采样阶段、路径检查阶段和路径规划阶段的时间消耗，使算法的时间复杂度大幅提升。为此，从PRM算法的采样阶段入手，通过提高采样点的质量，增加处于障碍间狭窄区域的节点数目[9-12]。Amato 等[9]提出了基于障碍物的PRM 算法，该算法在采样阶段以均匀分布方式，一次生成两个节点，当两个节点中一个处于自由空间，另一个处于障碍空间时，以二分法，查找两节点间恰好处于自由空间的节点，并将该节点加入路径规划器。Boor 等[10]提出了基于高斯采样的PRM 算法，在采样过程中，该算法先以均匀分布生成一个节点，再以该节点为中心，以高斯分布生成另一节点，当上述两节点，分别处于自由空间和障碍空间时，将自由空间节点加入路径规划器。但上述两种算法，易使采用点落于障碍区域外侧，狭窄区域节点的采样效率低。Hus 等[11]将桥试验法引入PRM 算法，该算法需检测线段的两端点和中心点，当两端点处于障碍空间，中心点处于自由空间时，将中心点加入路径规划器。钟建冬等[12]用星形试验法增加狭窄通道的节点密度，该算法需检测2 个正交线段的2 对端点和中心点，当中心点处于自由空间，至少1 对端点处于障碍空间时，中心点即为所需。但上述两种算法使狭窄区域节点过多，使开阔区域的规划差。上述4 种改良算法，对机械臂避障路径规划，由于关节空间与笛卡尔空间具有复杂的映射关系，故采样过程会有很大的时间消耗。

本文建立节点势能评价指标，定义困难区域节点，将障碍空间节点利用Metropolis 准则向困难区域调整，获得一个性能更优良的PRM 算法，将该算法应用于机械臂路径规划，并验证方法的有效性。

1 引入势能函数的PRM 算法

1.1 势能函数和困难区域节点的定义

对节点进行评价，需建立其势能评价标准，势能函数包含引力势能和斥力势能，分别为：

由式（1）和式（2）得势能函数为

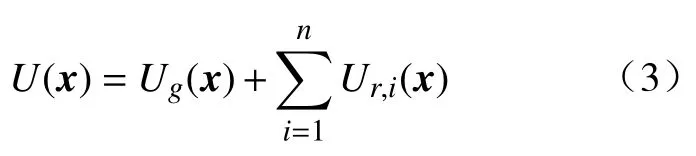
式（1）～（3）中：x为规划空间中一点；goal为目标点；Oi和Ri为障碍i的中心点和危险距离；n为障碍数目；l为避障刚体的危险距离；s为安全距离；Dg(x,goal)是关于x和goal的距离函数；Dr(x,Oi)是关于x和Oi的距离函数；Ug(x)为引力函数；Ur,i(x)为x相对i的斥力函数；λ和 η为引力常数和斥力常数，且λ ＞＞η ＞0，以保证处于障碍空间的点对应的势能大于处于自由空间的点。

欲实现障碍空间点向障碍间狭窄区域调整，需定义x*：对∀k,z=1,2,···,n且k≠z，若

则x*为困难区域节点。

式中：Cobs为障碍空间；σ为困难区域节点的判定距离，σ通过将原有的障碍空间增大，从而寻找出至少离两个障碍较近的节点。

1.2 调整策略

先求得障碍空间节点集合、困难区域节点集合，再将障碍空间节点集合中所有节点，随机的向困难区域节点集合中的某一点调整，并根据势能指标，依概率决定调整是否成功，直至所有障碍空间节点均完成调整。节点位置调整和概率选择式分别为：

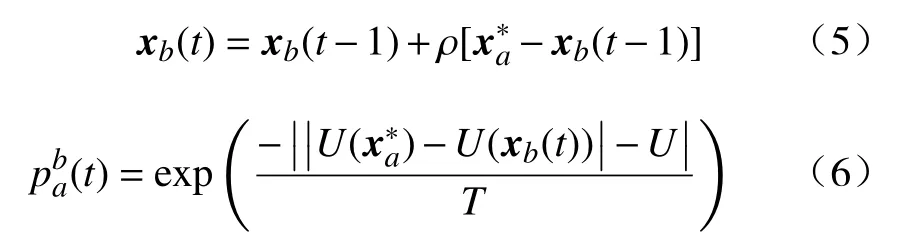
式中：T是正常数；t为调整次数；ρ为（0,1）上的随机数；xb(t)和xb(t-1)为障碍空间节点b调整后和调整前的坐标；为困难区域节点a的坐标；U为正的势能常数，用以防止困难区域节点距离过近造成的节点多样性丧失；为调整次数为t时，调整成功的概率，操作中，随机生成一个（0,1）的随机数p，当＞p时，b接受调整；反之，b不接受，随机再选择一个困难区域节点，以b更新后的位置重新调整。

式（6）是依据模拟退火算法Metropolis 准则[13]设置，当调整后节点b离a较远或依然处于障碍空间时，较大，使得较小，调整成功率低；当调整后节点b离a过近时，由于U使得较小，调整成功率低，从而防止过多的困难区域节点聚集在一起；当节点b离a距离合适时，接近0，较大，调整成功率高。

1.3 势能代价PRM 算法流程

步骤1 在需规划的状态空间中随机采点，求出障碍空间节点集合H、自由空间节点集合I，困难区域节点集合G，计算G中元素的势能，初始化U，令t=0，集合record为空集；

步骤2 判断H是否为空集，若为空，则执行步骤6；否则，计算t=t+1，h=1，M=size(H)（M为集合H中节点数），执行步骤3；

步骤3 判断h≤M是否成立，若不成立，则将H中record对应的h元素全部删除，跳转至步骤2；否则，执行步骤4；

步骤4 用式（5）将H中元素xh(t-1)向G中随机一个元素调整，计算p，xh(t)，U(xh(t))，

步骤6 安全路径检查，设置距离d，将安全路径中节点距离小于d的节点作为其相邻节点，并用A*算法进行路径规划；

步骤7 算法结束。

2 势能代价PRM 算法机械臂避障规划

机械臂关节空间搜索的优点：1）无需考虑机械臂逆运动学解[14]的存在性和唯一性；2）可避免机械臂的奇异位形[15]；3）避免笛卡尔空间中机械臂末端姿态难以测量的问题。选择在q1q2,···,qN（N为机械臂自由度）的关节空间中进行路径搜索。

2.1 连杆势能函数的建立

机械臂的规划空间中，障碍和其连杆的形状不规则，难以建立精确的势能表达式，因此需对连杆和障碍简化。对连杆作圆柱包围体简化，障碍作球包围体简化。∠Okαj(q)βj(q)与∠Okβj(q)αj(q)均小于90°，如图1 所示，∠Okαj(q)βj(q) 与∠Okβj(q)αj(q)有一角大于90°，如图2 所示。

图1 ∠Okαj(q)βj(q) 与∠Okβj(q)αj(q)均小于90°

图2 ∠Okαj(q)βj(q) 与∠Okβj(q)αj(q)有一角大于90°

令图1 和图2 中∠Okαj(q)βj(q) 为φ，∠Okβj(q)αj(q)为θ，建立连杆的势能函数。

1）如图1 所示，当φ与θ 均小于90°时

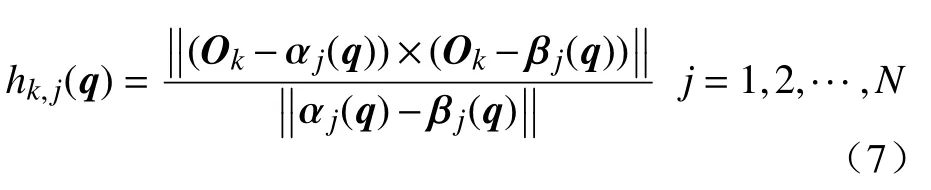
式中：q=[q1,q2,···,qN]；αj(q)和βj(q)分别为连杆两端中心的位置矢量，均是q的函数，由机械臂正向运动学[16]求出。

2）如图2 所示，当φ 与θ 有一个角大于90°时

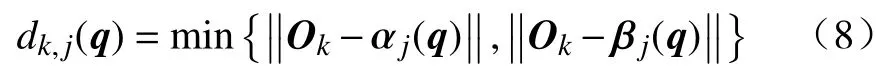
综合图1 和图2，连杆j与障碍k的距离distk,j(q)定义为：

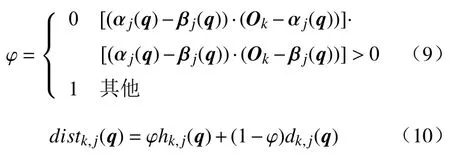
由式（1）～式（3），连杆势能函数U(q)为：

式中：rj为连杆j的圆柱半径；Rk为障碍k的半径。

2.2 安全路径检查

构建算法路线图时，需要判断两个构型qA，qB之间是否经过障碍。对机械臂，两个不同构形的同一连杆的空间关系存在异面、相交、平行、重合，难以用连续的方式判断，因此用离散方式，具体步骤如下：

步骤1 令m=1，初始化阈值E，a=‖qB-qA‖。

步骤3 计算K=0,1,···,2m-1-1，qtext=qA+，判断distk,j(qtext)＞Rk+rj+s是否全部成立，若成立，m=m+1，执行步骤2，否则，执行步骤4。

步骤4 算法结束，qA，qB间经过障碍。

步骤5 算法结束，qA，qB间不经过障碍。

上述方法，依次将qA与qB在N维状态空间中连线2m(m=1,2,···)等分，并依次判断所有2m等分点处的碰撞情况，当发现等分点处存在碰撞时，认为qA，qB间经过障碍；当≤E且所有等分点均不碰撞时，认为qA，qB间不经过障碍。

2.3 机械臂避障路径规划算法流程

步骤1 在q1,q2,···,qN空间中随机采点，求出障碍空间节点集合H、自由空间节点集合I，困难区域节点集合G，计算G中元素的势能，初始化U，令t=0，集合record为空集。

步骤2 判断H是否为空集，若为空，则执行步骤6；否则，计算t=t+1，h=1，M=size(H) (M为集合H中节点数目)，执行步骤3。

步骤3 判断h≤M是否成立，若不成立，则将H中record对应的h元素全部删除，跳转至步骤2；否则，执行步骤4。

步骤4 用式（5）将H中元素qh(t-1)向G中随机一个元素调整，计算p=rand，由式（5）计算qh(t)，由式（13）计算U(qh(t))，由式（6）计算

步骤6 用2.2 节的方法进行安全路径检查，设置距离d，将安全路径中与节点距离小于d的节点作为其相邻节点，并用A*算法进行路径规划。

步骤7 算法结束。

3 仿真验证

3.1 势能代价PRM 算法性能分析

为了测试势能代价PRM 算法（提出算法）的性能，本文将其与PRM、OBPRM[9]、高斯采样PRM 算法[10]进行对比测试。在自由空间节点数目相同的条件下，规划结果优劣的评价指标：成功率SUC和规划路程代价S，表达式为：

式中：M为算法独立运行的次数；Msuc为在M次独立运行中，算法规划成功的次数；Sγ为第 γ次路径规划成功时，规划路程代价；mγ为第 γ次路径规划成功时，相邻节点的间隔总数。

规划的时间消耗也是算法的重要性能指标，如果一个算法优化结果质量的提升，是以大幅增加其时间复杂度为代价，该算法往往不能被接受。本文在自由空间采用点数目相同条件下，比较各算法的规划时间。

为了直观体现所有算法在规划空间的采点情况，先将其用于3 种不同环境下的质点避障规划；同时为了提高结果的可信度，将所有算法对同一问题独立运行20 次。所有算法的参数设置见表1；所有算法的成功率SUC、规划路程代价S和优化时间t指标的均值见表2；所有算法的某次采样及规划情况如图3～ 图5 所示（图中黄线表示规划路径，红点表示自由空间采样点，圆表示障碍空间，图3b）、图4b）和图5b）中绿点表示障碍空间节点向困难区域节点调整成功后的位置)。

表1 算法的参数设置

由表2 可知：环境1 下，提出算法的SUC比PRM、高斯采样PRM、OBPRM 算法分别多75%、15%、15%，其S相对PRM、高斯采样PRM、OBPRM 算法分别降低了7.19%、4.28%、2.84%，其t相对PRM、高斯采样PRM、OBPRM 算法分别降低了4.33%、12.82%、6.91%；环境2 下，提出算法的SUC比PRM、高斯采样PRM、OBPRM 算法分别多80%、20%、25%，其S相对PRM、高斯采样PRM、OBPRM 算法分别降低了8.98%、5.17%、4.31%，其t相对PRM、高斯采样PRM、OBPRM 算法分别降低了8.11%、15.44%、10.55%；环境3 下，提出算法的SUC比PRM、高斯采样PRM、OBPRM 算法分别多30%、0%、5%，其S相对PRM、高斯采样PRM、OBPRM 算法分别降低了8.04%、3.95%、4.88%，其t相对PRM、高斯采样PRM、OBPRM 算法分别降低了4.33%、10.39%、10.29%。可见，势能代价PRM算法的规划结果优于其他3 种算法，且规划时间少。由图3b），图4b)和图5b）知，障碍空间节点调整成功后，其中绝大部分节点落在了障碍间狭窄区域，提高了PRM 算法通过狭窄区域的能力。

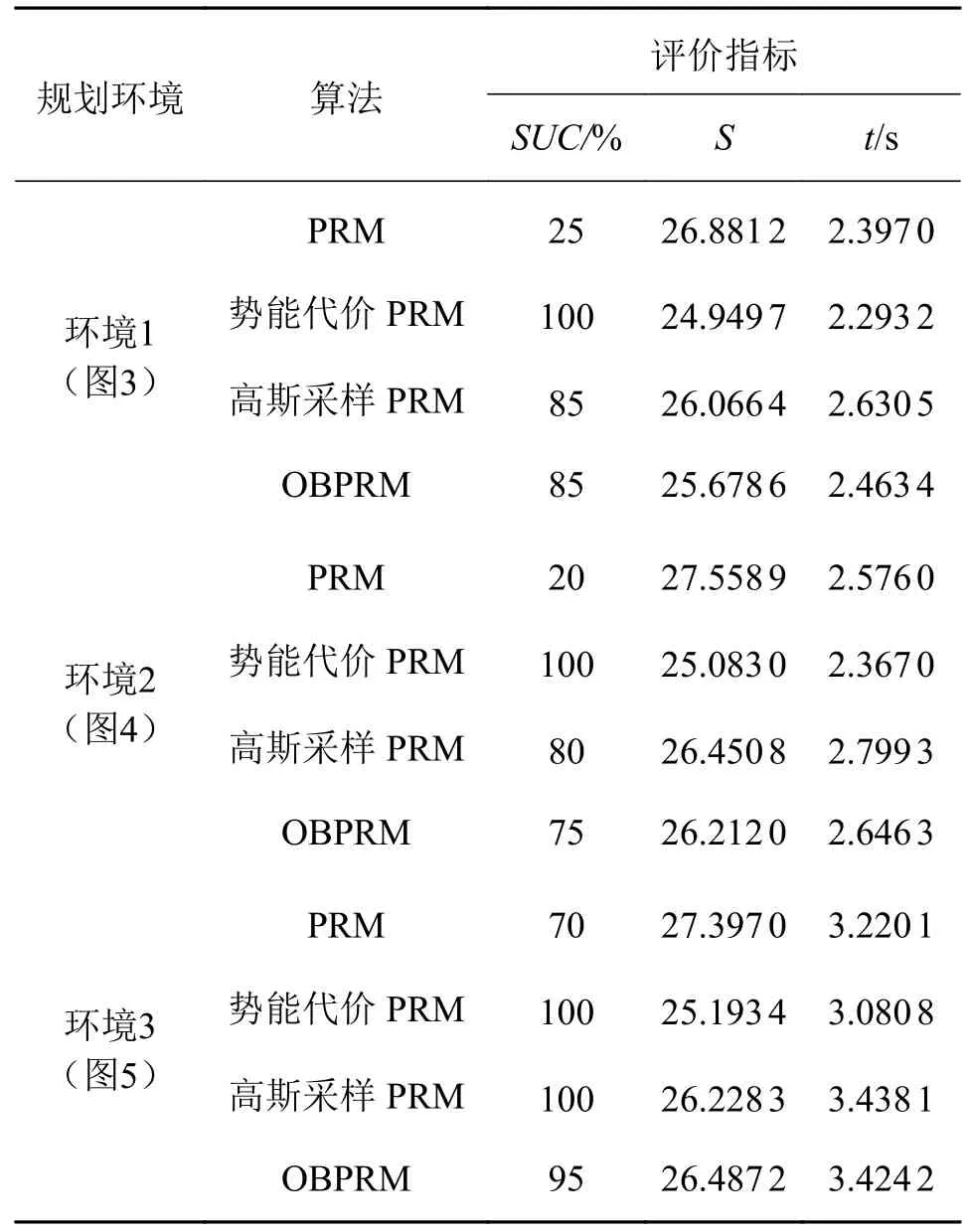
表2 算法的SUC、S 和t

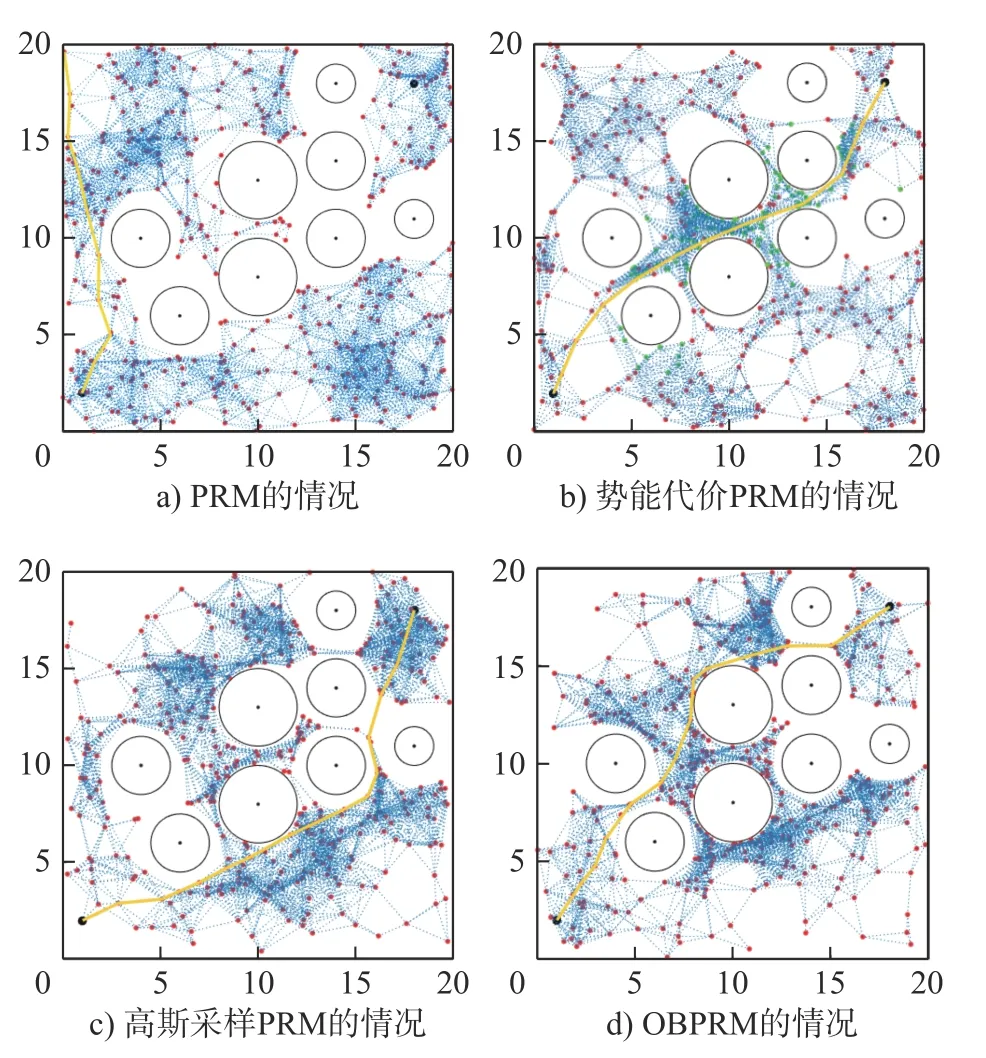
图3 环境1 下4 种算法的采样及规划情况

图4 环境2 下4 种算法的采样及规划情况

图5 环境3 下4 种算法的采样及规划情况

3.2 机械臂避障规划问题的结果分析

将上述4 种算法应用于机械臂避障路径规划问题，测试环境同3.1 节，且每种算法均对同一问题独立运行20 次。选取的KR5 机械臂的D-H 参数[16]如表3 所示。算法的参数设置如表4 所示。所有算法的SUC、S和t的均值如表5 所示。提出算法的规划情况如图6～ 图9所示（图中绿线、黑线、粉线、蓝线、红虚线分别表示关节2、3、4、5、6 在笛卡尔空间的运动轨迹，左侧机械臂为起始位姿）。

表3 KR5 机械臂D-H 参数

表4 算法的参数设置

由表5 可知，在环境1～ 2 下，虽PRM 算法的规划时间显著低于势能代价PRM 算法，但由于其SUC在两种环境下分别为5%和15%（即20 次运行只有1 次和3 次规划成功），且在环境3～ 4 下，PRM 算法没有规划成功，而提出算法在4 种环境中SUC均为100%，因此提出算法的规划性能优于PRM 算法；在环境1～ 4 下，提出算法的SUC比OBPRM 算法分别多70%、45%、100%、100%，在环境1～2 下，其S相对OBPRM 算法分别降低了4.67%和3.61%，其t相对OBPRM 算法分别降低了32.00%和32.50%，因此提出算法的规划结果和时间均优于OBPRM 算法；在环境1～ 4 下，提出算法的SUC比高斯采样PRM 算法分别多0%、0%、10%、0%，其S相对高斯采样PRM 算法分别降低了6.63%、4.79%、11.03%、7.67%，其t相对高斯采样PRM 算法分别降低了57.12%、56.44%、63.03%、57.91%，因此提出算法的规划结果略优于高斯采样PRM 算法，规划时间优于高斯采样PRM 算法。

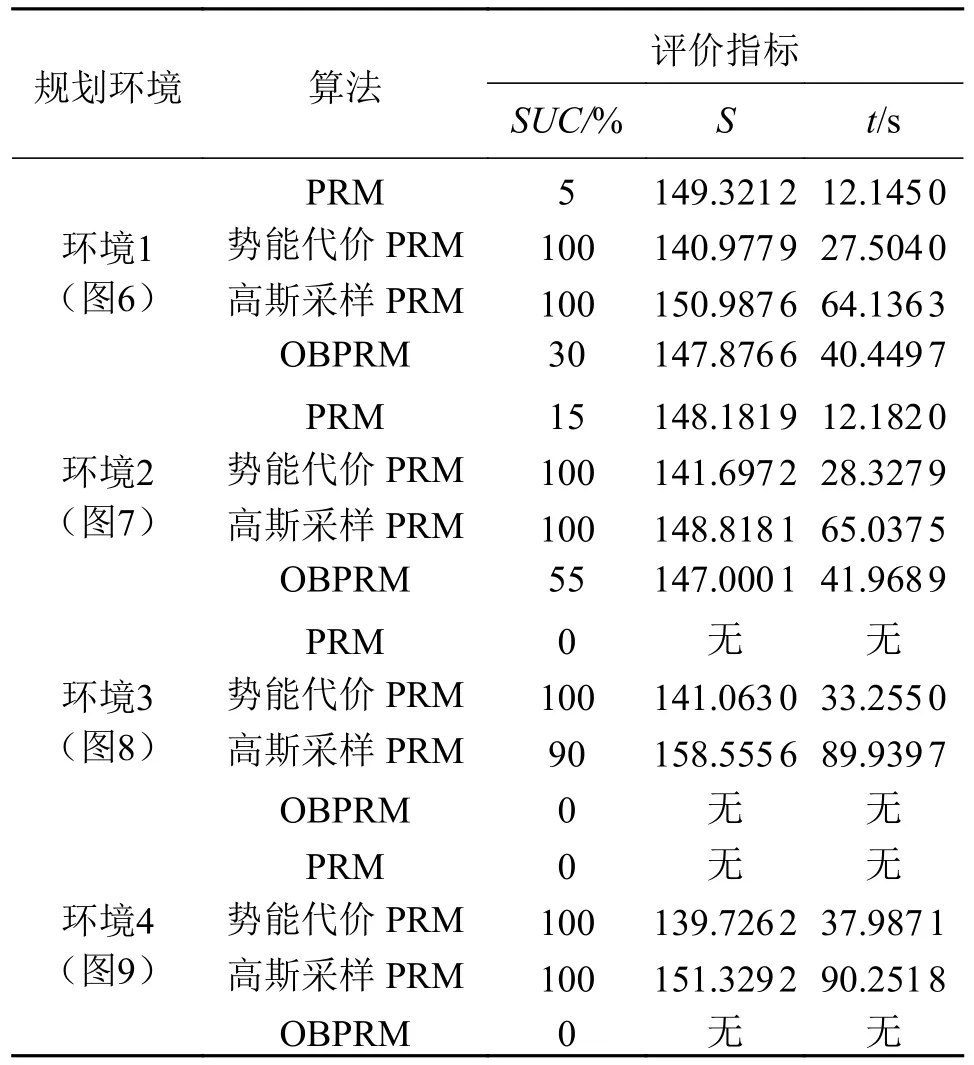
表5 算法的SUC、S 和t 均值

由图6～ 图9 可知，提出算法能使机械臂躲避所有障碍，并到达目标位姿。

图6 提出算法在环境1 下的规划情况

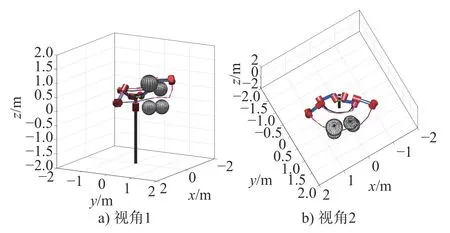
图7 提出算法在环境2 下的规划情况

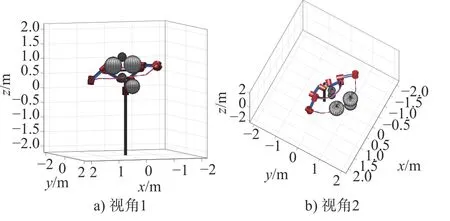
图8 提出算法在环境3 下的规划情况

图9 提出算法在环境4 下的规划情况

4 结论

1）在算法的性能分析中，势能代价PRM 算法的SUC相对PRM、高斯采样PRM、OBPRM 算法分别至少多30%、0%、5%，其S相对PRM、高斯采样PRM、OBPRM 算法分别至少降低了7.19%、3.95%、2.84%，其t相对PRM、高斯采样PRM、OBPRM 算法分别至少降低了4.33%、10.39%、6.91%，由此可见在性能上，提出算法在规划结果和时间上均优于PRM、高斯采样PRM 和OBPRM 算法；且障碍空间节点调整成功后能落在了障碍间狭窄区域。

2）在机械臂避障路径规划问题上，势能代价PRM 算法的规划时间虽多于PRM 算法，但提出算法的SUC至少比PRM 算法多85%，且其SUC分别至少比高斯采样PRM、OBPRM 算法多0%、45%，其S分别至少比高斯采样PRM、OBPRM 算法降低了4.79%、3.91%，其t分别至少比高斯采样PRM、OBPRM 算法降低了56.44%、32.00%，由此可见在该问题上，提出算法的规划性能优于PRM、高斯采样PRM 和OBPRM 算法。

3）势能代价PRM 算法能使机械臂在规划中避开所有障碍，并到达目标构型。