多维性能极限状态下基于模糊失效准则的结构概率地震风险分析
2022-05-14贾大卫吴子燕何乡
贾大卫 吴子燕 何乡





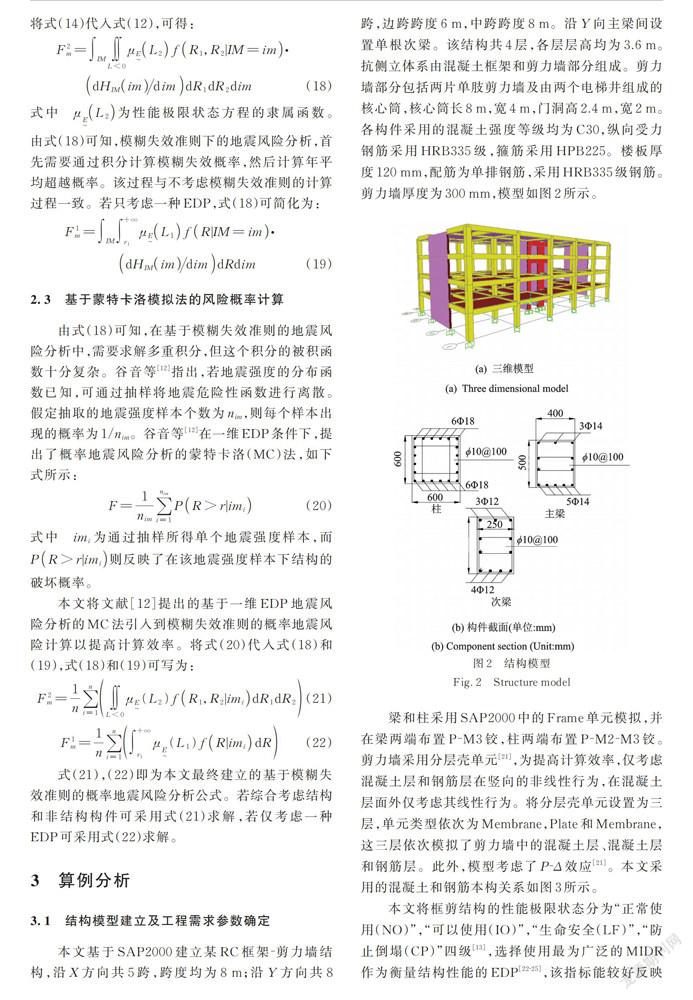
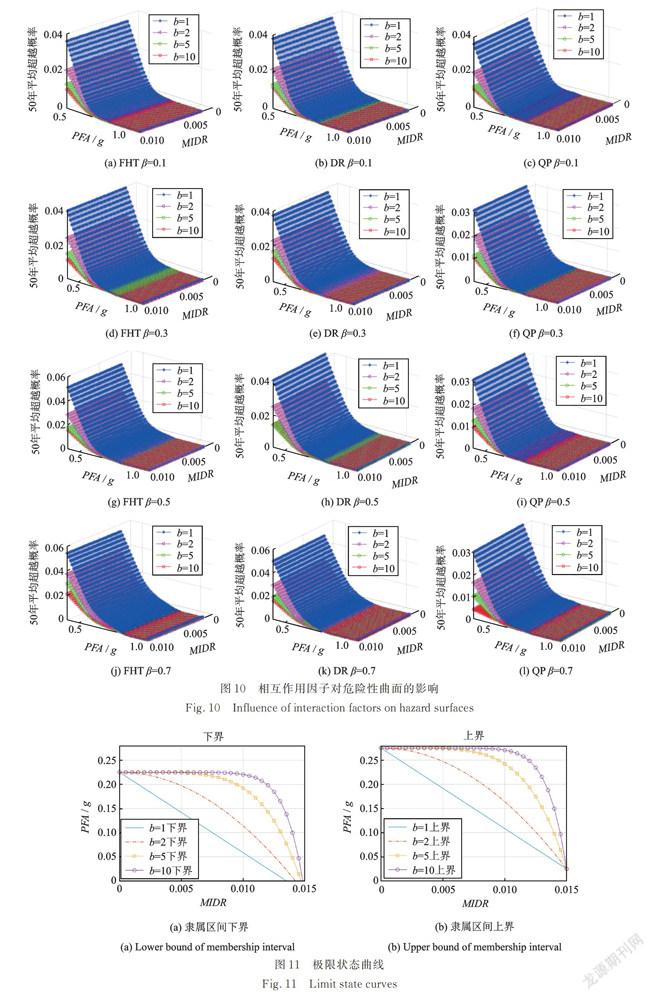

摘要: 考虑了结构多维性能极限状态的模糊不确定性,建立基于模糊失效准则的概率地震风险分析方法。综合考虑结构和非结构构件的抗震性能,建立多维性能极限状态方程。选择三种隶属函数描述极限状态的模糊性,包括降半梯形分布、降岭型分布和二次抛物型分布,基于地震烈度概率模型,建立基于模糊失效准则的概率地震风险分析表达式。基于SAP2000建立RC框剪结构模型进行分析。研究表明:基于二次抛物型分布的年平均超越概率会随着隶属区间的扩大而减小,而基于降半梯形分布和降岭型分布的年平均超越概率会随着隶属区间的扩大而增大;若隶属区间相同,三种隶属函数的年平均超越概率,从大到小依次为降半梯形分布、降岭型分布、二次抛物型分布;忽略不同工程需求参数性能极限状态的相关性会使年平均超越概率偏低。
关键词: 概率地震风险分析; 框剪结构; 多维性能极限状态; 模糊失效准则; 隶属函数
中图分类号: TU311.3; TU352.1 文献标志码: A 文章编号: 1004-4523(2022)02-0307-11
DOI:10.16385/j.cnki.issn.1004-4523.2022.02.006
引 言
建筑结构的抗震性能通常受到结构构件和非结构构件的共同影响,而且实际使用功能绝大多数都依赖于非结构构件,因此在进行抗震性能评估时需要同时考虑结构性能和非结构性能。美国太平洋地震工程研究中心(PEER)对此进行了大量研究,率先提出新一代“基于性能的地震工程”(PBEE)概率决策框架。近几年第二代PBEE理论也逐渐完善,该研究框架的基础为概率地震风险分析,主要用来计算结构在具体场地条件下超过给定性能极限状态的年平均超越概率。概率地震风险分析是场地概率地震危险性分析与结构地震易损性分析相结合的产物,是指在考虑场地风险的情况下,结构发生不同损伤程度的可能性。
国内外学者开展了大量有关概率地震风险的研究,并取得了丰硕的成果,例如:Banihashemi等基于最大层间位移角(MIDR),进行了钢框架的地震易损性和可靠性分析;Moradi等通过代理模型法,基于MIDR和局部支撑结构的应变,建立了参数化易损性分析方法;Alih等研究了机场塔台结构,考虑到各层承担功能的不同,通过非线性时程分析法进行了结构整体的抗震性能研究;Javidan等基于神经网络,建立了结构地震易损性分析的快速评估模型;蒋亦庞等考虑结构参数的不确定性,建立了无筋砌体结构的地震易损性曲线,并探讨了结构参数的不确定性对结构性能的影响;盛金喜等考虑了近断层地震的方向性对框架结构的影响,分别建立了易损性曲线和易损性指数曲线;Khaloo等基于桥墩柱的最大弯曲延性响应,考虑结构的时变损伤模型,建立了易损性曲线;钟剑等基于全概率理论进行了桥梁结构的地震风险分析。上述研究存在不足之处:其一,部分研究仅针对结构构件进行地震易损性分析,未考虑非结构构件的性能;其二,绝大多数研究仅考虑了在不同地震强度下结构达到指定性能极限状态的概率,即只进行了易损性分析,并未涉及场地风险分析;其三,在基于性能的地震工程研究中,需要将结构的性能极限状态分为多个等级,目前研究人员划分的依据主要是工程需求参数(EDP)在性能极限状态下的阈值,当EDP超过阈值则代表进入新的状态。绝大多数研究采用精确的失效准则,即不同性能极限状态下阈值为固定值。固定阈值的失效准则假定结构完全处于某种状态,是一种“一刀切”的抽象方法。但在实际工程中,极限状态的边界是模糊不确定的,结构从状态A进入状态B,中间通常存在一个过渡带。例如《建筑抗震设计规范》 (GB 50011—2010)中规定RC框架类结构最大层间位移角(MIDR)在彈塑性状态下不能超过1/50。若震后MIDR为1/49.5,此时有很大可能结构仍处于安全状态,若采用固定阈值则会认为结构已经发生破坏。因此该方法并不完全符合工程实际。
为解决上述问题,本文将模糊失效准则引入概率地震风险分析理论。以RC框架⁃剪力墙结构为例,首先建立多维性能极限状态下基于固定阈值的概率地震风险分析公式,然后引入隶属函数,将极限状态边界视为模糊不确定的,建立基于模糊失效准则的地震风险分析公式,最后将年平均超越概率用危险性曲面的形式表示,并探讨不同的隶属函数和隶属区间对年平均超越概率的影响。
