混凝土单轴受拉断裂行为的近场动力学模拟

张晨明，侯东帅，张洪智，张 伟

(1.青岛理工大学土木工程学院，青岛 266520；2.山东大学齐鲁交通学院，济南 250002)

0 引 言

作为建筑结构中最重要的材料之一，混凝土的用量巨大。然而混凝土中裂缝的存在会导致其力学性能劣化甚至破坏。因此，研究混凝土中裂缝的萌生和扩展机理对预测和预防混凝土开裂具有重要意义。尽管国内外众多学者[1-2]对混凝土开展了众多研究，但其破坏机理仍有待深入探索。目前数值模型是研究混凝土断裂问题的有效途径，传统的混凝土数值模型主要包括粘聚区模型(CZM)[3-6]、有限元模型(FEM)[7-10]、扩展有限元模型(EFEM)[11-14]，以及格构模型[15-17]等。其理论基础是基于空间偏微分方程和连续性假设的断裂力学理论，而裂缝出现时会造成裂缝尖端位移场不连续，即此处的偏导数不存在，因而偏微分方程中的空间导数便失去了意义。传统力学的另一个假设是局部性假设，即认为某质点的应力状态只取决于该质点处的变形。该假设在宏观尺度一般是可接受的，但当尺度进一步缩小时，局部作用假设的精度就会降低。此外，传统数值模拟方法在分析断裂问题时需要划分网格或者预设裂纹路径，因此在预测裂缝萌生和扩展方面还存在着精度和计算效率方面的困难[18-19]。

近年来，一种新兴的非局部理论近场动力学[20-22](peridynamics，PD)的提出，为进一步研究混凝土的断裂机理提供了另一种方案。与基于连续性假设的断裂力学理论不同的是，前者采用偏微分方程，而PD理论采用空间积分方程和时间微分方程来描述不连续现象，质点与一定距离内的其他质点相互作用，而不仅仅是与相邻的质点相互作用。因此，在没有附加修正准则的情况下，可以避免裂纹尖端位移场的不连续性，使裂纹能够在物体中自然萌生、扩展和分支。基于此，利用PD理论可以对许多传统的混凝土动、静态断裂问题进行更加合理的研究。如Huang等[23]建立了混凝土板的数值模型，采用PD理论分析了其在冲击荷载和静态荷载作用下的损伤形式。考虑到水泥砂浆在细观尺度上的非均质性，Hou等[24]利用PD理论对水泥砂浆的断裂性能和应力应变响应进行了研究。此外，已有文献报道了PD理论和FEM的耦合工作。Oterkus等[25]研究了复合结构加筋板在轴向拉伸荷载下的损伤过程，结果与实验现象吻合较好。为了充分利用PD和FEM的优点，Liu等[26]引入界面单元对PD区域和FEM区域进行耦合，通过对三维杆件的研究，验证了耦合损伤方法的合理性。在这些研究中，PD理论在处理断裂、失稳和冲击等方面的可靠性得到了成功验证。但目前应用PD理论研究混凝土却较少涉及其多相非均质性，因此，本文通过构建由多相材料组成的混凝土数值模型，对其在单轴拉伸作用下的力学性能和断裂特征进行了研究。

1 模拟方法

1.1 近场动力学简介

图1为原始微观弹脆性模型(original micro-elastic brittle model)中质点间的相互作用力。如图1所示，近场动力学理论假定物体占据空间某一区域，通过研究某一质点x与其影响区域(近场范围δ)内的其他质点间的相互作用来分析物体的运动。在任一时刻t，质点x近场范围内的质点称为x的族Hx，超出族Hx以外的质点将不与x发生相互作用。类似地，质点y也仅与族Hy内的质点存在相互作用。根据牛顿第二运动定律，其基本运动方程可用式(1)表示：

图1 原始微观弹脆性模型中质点间的相互作用力

(1)

两质点的位置矢量和位移矢量可分别表示为ξ=y-x和η=u(y)-u(x)，则运动方程可简化为：

(2)

根据牛顿第三运动定律，本构力函数f必须满足：

f(-η,-ξ)=-f(η,ξ)

(3)

作为键基近场动力学理论中最常用的一种，原始微观弹脆性模型忽略横向和剪切变形，假定质点间的成对等值相互作用力(又称为键力)只取决于质点间键的伸长率。对于由单层材料组成的近似二维物体，本构力函数f可表示为：

(4)

(5)

(6)

式中：c为质点间的键刚度；s为键的伸长率；k为材料的体积模量；h为单层材料点的厚度。

原始微观弹脆性模型的本构模型可用图2表示。在线弹性阶段，本构力函数f与伸长率s呈线性增加关系，当伸长率s超过某一阈值s0，质点间的相互作用将会不复存在。键的状态μ可用式(7)表示：

图2 材料受拉的本构模型

(7)

质点x的损伤可被定义为：

(8)

损伤D(x,t)的取值范围为0～1，当损伤为0时代表质点处于弹性阶段，损伤为1时表示质点完全发生破坏，一般认为，当损伤≥0.5时就会有裂缝产生[27]。

1.2 模型构建和参数设置

本文基于随机骨料模型[28]和蒙特卡罗法[29]开展研究。模型尺寸如图3所示，骨料形状为球形，粒径范围为3～8 mm，符合富勒级配，骨料体积比为40%。模型分辨率为0.4 mm，共包含76 576个质点。根据数值模型中的质点位置将其分为两类：骨料质点和砂浆质点，因此形成了砂浆-砂浆键、骨料-骨料键以及砂浆-骨料(ITZ)键。近场作用范围δ=1.2 mm，各类型键刚度c可通过式(5)计算，模型在x和y方向均为自由边界。借助LAMMPS软件，对数值试件上下端25 mm范围内赋予1 μm/s的初始速度开始拉伸直至完全破坏。

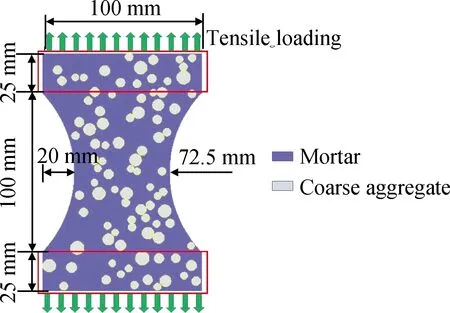
图3 单轴拉伸模型

2 结果与讨论

2.1 数值算例

采用表1所示的各相材料力学参数(下文各相材料的弹性模量和抗拉强度分别用EA、EM、EITZ、fTA、fTM以及fTITZ表示)，数值试件的应力-应变关系和断裂过程如图4所示。在单轴拉伸荷载作用下，数值试件首先进入线弹性阶段(O-A段)，此过程质点间的键几乎不发生断裂，没有微裂缝萌生；随着变形的增大，试件应力逐渐增大直至达到峰值应力(A-B段)，此过程质点间的键开始发生断裂，裂缝从ITZ区域的多个位置萌生；接着进入下降段(B-C段)，此时质点间键的断裂数量急剧增加，裂缝逐步扩展并形成贯通的主裂缝(C-D段)，导致试件发生破坏。值得注意的是，本文中的力学曲线中基本没有出现软化段，这主要是因为键基近场动力学本构关系忽略了砂浆在更小尺度的延性[30-31]。根据结果可知，正是骨料和砂浆之间存在的薄弱区域(ITZ)造成了混凝土在外荷载下的开裂以致破坏。从力学曲线和断裂过程来看，所建立的数值模型能较好地对应混凝土在单轴拉伸作用下的力学行为。

表1 数值模型的各相力学参数

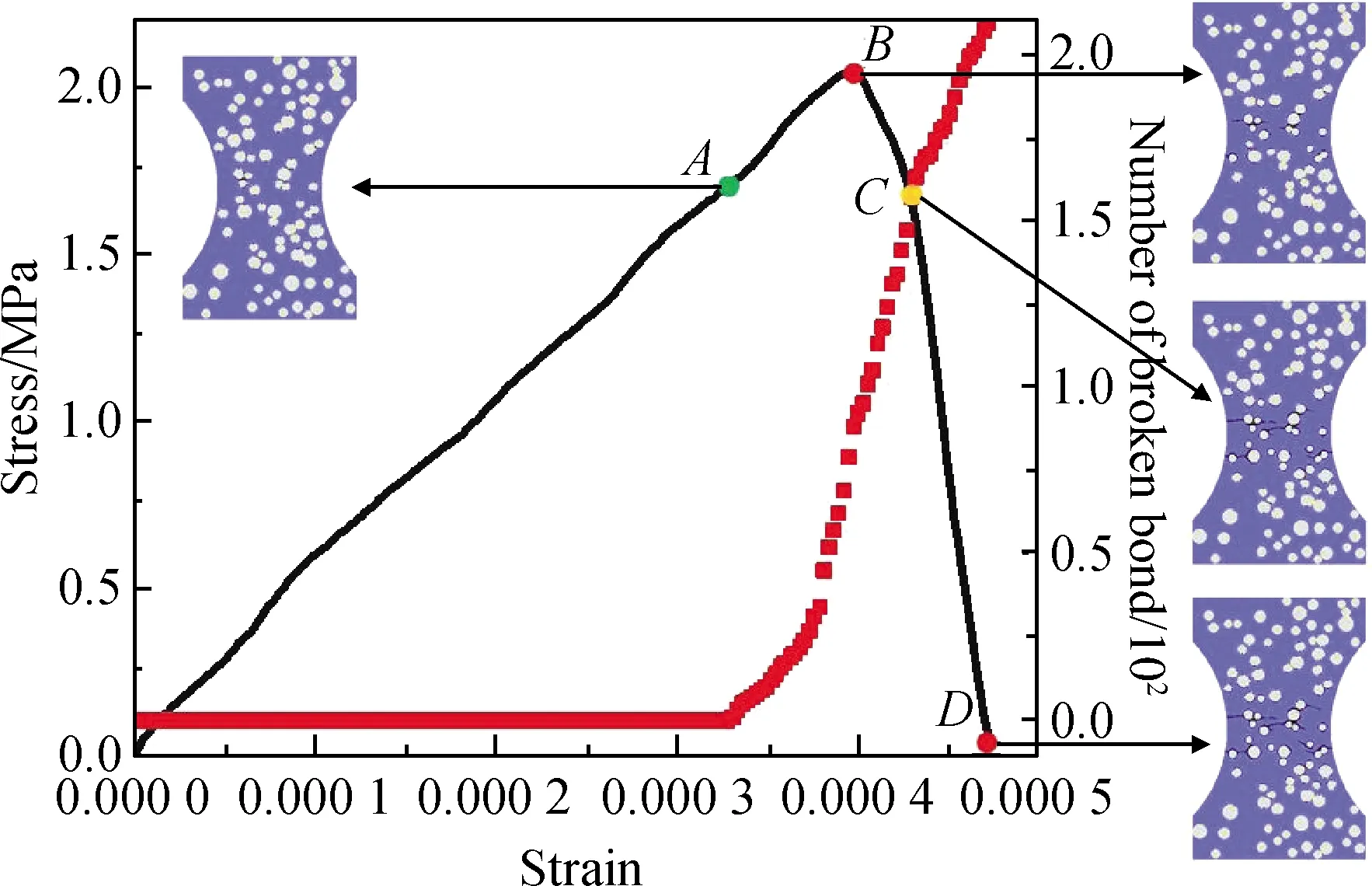
图4 单轴拉伸载荷下数值模型的应力应变关系及断裂键数与应变的关系

2.2 粗骨料含量的影响

保持各相力学参数不变，对粗骨料含量分别为30%、40%和50%(均为体积分数)的数值试件进行单轴拉伸模拟。图5为三种粗骨料含量下的应力-应变曲线。如图5所示，随着粗骨料含量的升高，在线弹性阶段，各试件弹性模量和抗拉强度均逐渐降低，达到峰值应力时所对应的峰值应变逐渐减小。具体来说，在达到峰值应力时，粗骨料含量为30%、40%和50%对应的应变分别为4.06×10-4、3.98×10-4和3.42×10-4。这是因为随着粗骨料含量的增多，砂浆与粗骨料之间的薄弱区域(ITZ)也随之增加。将应力-应变曲线进行归一化处理后(见图6)，结果表明50%粗骨料含量的试件延性最高。这主要是因为随着粗骨料含量的增加，ITZ也随之增加，结合三种粗骨料含量下数值试件破坏形态(见图7)可知，与含30%和40%粗骨料的数值试件相比，含有50%粗骨料数值试件的ITZ区域萌生了更多的裂缝，因而拉伸过程中消耗了更多能量，延性较前两者略好。

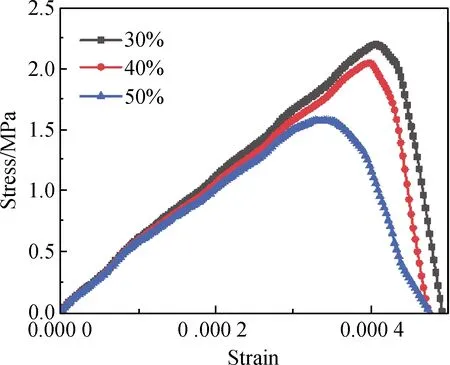
图5 三种粗骨料含量下数值试件的应力-应变曲线

图6 三种粗骨料含量下数值试件的归一化应力-应变曲线

图7 三种粗骨料含量下数值试件的破坏形态

2.3 ITZ抗拉强度的影响

数值算例中fTA∶fTM∶fTITZ=20∶10∶1，通过改变fTITZ的值研究了其对数值试件力学性能的影响。图8为不同ITZ强度下的应力-应变曲线。由图8可知，在单轴拉伸荷载作用下，数值试件的抗拉强度随着fTITZ的增强而提高。当ITZ不存在(即fTM=fTITZ)时，数值试件抗拉强度提高比较明显，说明混凝土均质性的提高有助于力学性能的提升。图9为不同ITZ强度下的归一化应力-应变曲线。图9表明，随着fTITZ的增大，数值试件脆性也呈现逐渐增大的趋势。

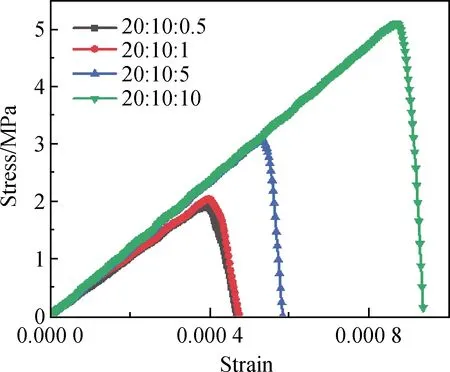
图8 不同ITZ强度下数值试件的应力-应变曲线

图9 不同ITZ强度下数值试件的归一化应力-应变曲线

通过对图10数值试件破坏的过程分析可知，当fTA∶fTM∶fTITZ=20∶10∶0.5和20∶10∶1时，随着变形的增加，裂缝均从多个ITZ区域萌生和扩展，最终形成贯通裂缝导致混凝土破坏。当fTA∶fTM∶fTITZ=20∶10∶5时，裂缝基本上只在试件截面中间位置的ITZ区域萌生，截面尺寸最小位置处的砂浆内部也会有少许裂缝萌生。随着进一步加载，两区域的裂缝逐渐扩展、交叉形成贯通裂缝。当fTA∶fTM∶fTITZ=20∶10∶10时，裂缝不再从ITZ区域萌生，而是从截面尺寸最小的位置萌生并逐步向试件内部扩展。此外，随着fTITZ的提高，出现损伤的ITZ区域逐渐减少，这也是造成含有较低强度ITZ的试件有较大延性的原因。

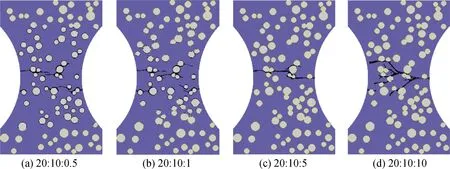
图10 不同ITZ强度下数值试件的最终破坏形态

2.4 粗骨料强度的影响

以数值算例为基准组(fTA∶fTM∶fTITZ=20∶10∶1)，保持砂浆和ITZ的力学参数不变，通过等比例改变粗骨料的弹性模量和抗拉强度，模拟了数值试件的力学响应和断裂形态。

图11为不同粗骨料强度下数值试件的应力-应变曲线。由图11可知，随着粗骨料力学性能的降低，数值试件的抗拉强度总体呈现降低趋势，但当fTA∶fTM∶fTITZ为10∶10∶1和5∶10∶1时，数值试件的抗拉强度反而上升。图12为不同粗骨料强度下数值试件的归一化应力-应变曲线。由图12可知，当fTA∶fTM∶fTITZ=10∶10∶1和5∶10∶1时，数值试件的延性要更好。

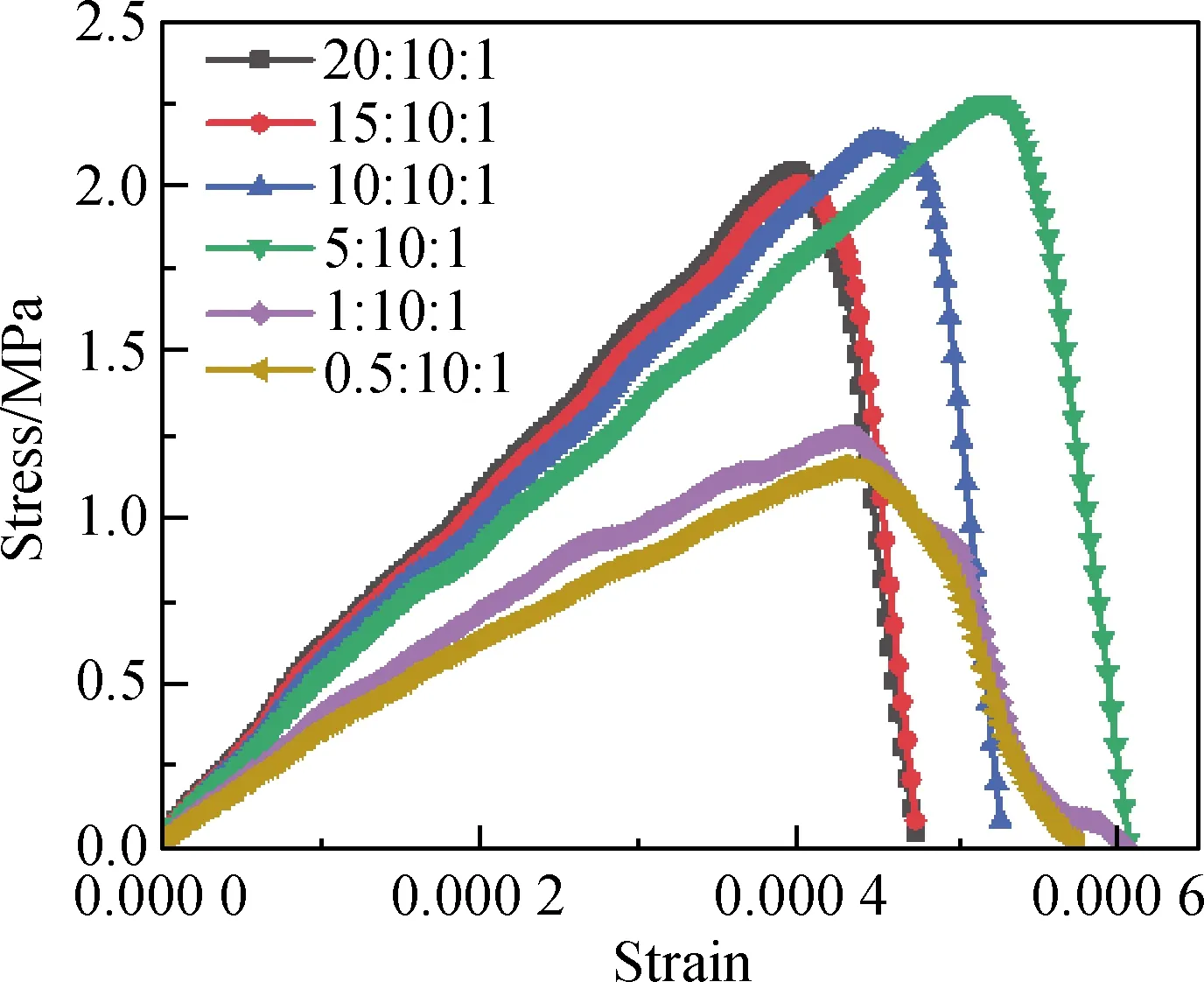
图11 不同粗骨料强度下数值试件的应力-应变曲线

图12 不同粗骨料强度下数值试件的归一化应力-应变曲线

图13为不同粗骨料强度下数值试件的最终破坏形态。由图13可知，当fTA∶fTM∶fTITZ=20∶10∶1、15∶10∶1、10∶10∶1和5∶10∶1时(见图13(a)～(d))，数值试件中裂缝的萌生、扩展以及最终断裂形态与基准组类似。与(a)、(b)两组相比，(c)、(d)两组在破坏时除了存在一条主裂缝以外，还萌生了一条次裂缝，因此断裂的键数更多，抗拉强度更高。当fTA∶fTM∶fTITZ=1∶10∶1和0.5∶10∶1时(见图13(e)和(f))，裂缝不只从ITZ区域萌生，而是在骨料内部和ITZ区域同时萌生并扩展，最后穿过骨料内部形成主裂缝，该情况与轻骨料混凝土的破坏形式[31]类似，因此通过改变骨料力学参数，本文所建立的模型也能较为合理地模拟出单轴拉伸荷载下轻骨料混凝土的破坏过程。

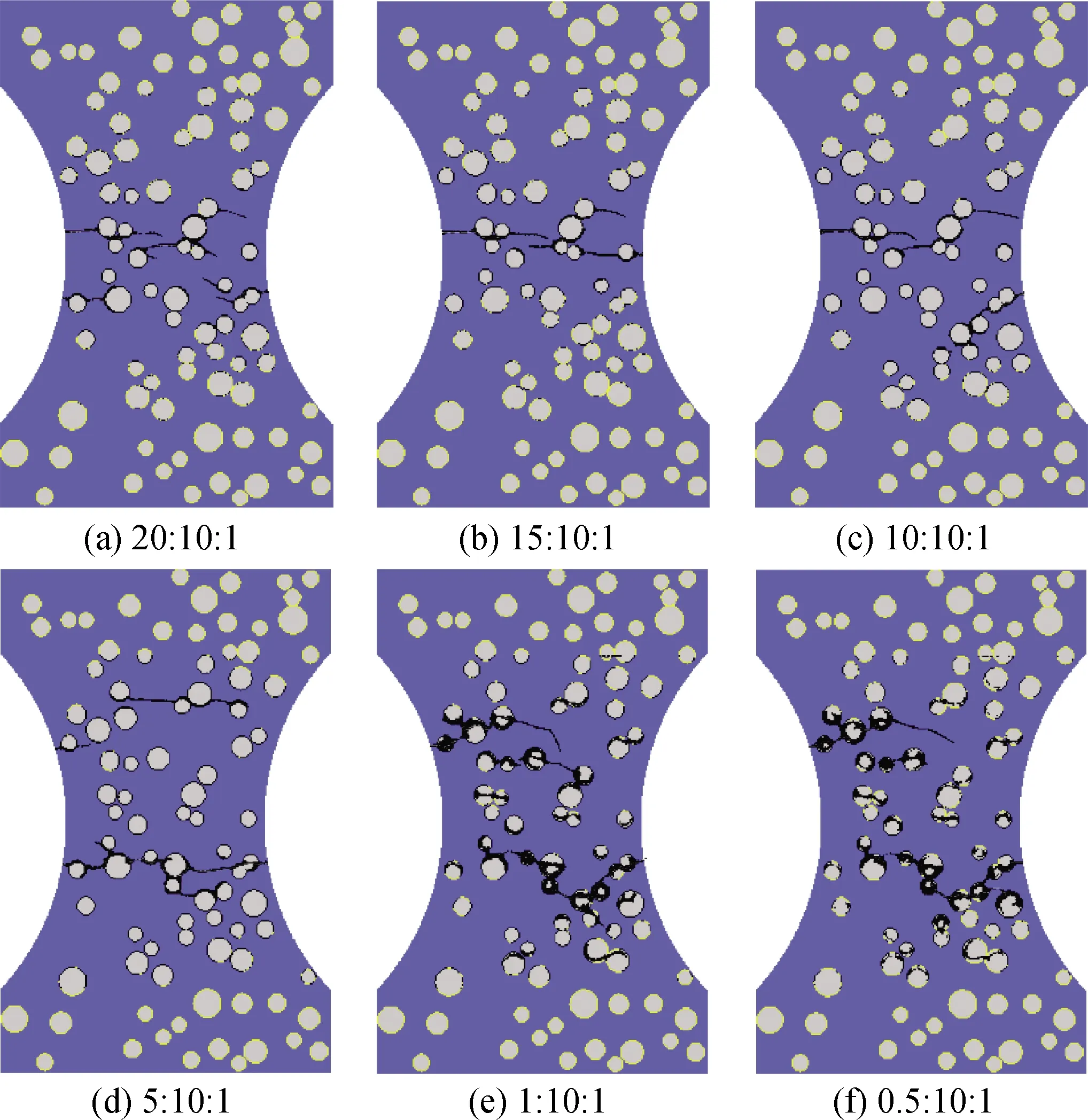
图13 不同粗骨料强度下数值试件的最终破坏形态

2.5 砂浆和ITZ抗拉强度的影响

以数值算例为基准组，保持骨料的力学参数不变，通过同比例增大砂浆和ITZ的弹性模量和抗拉强度，对数值试件的力学曲线和断裂形态进行了模拟。

图14为不同骨料和ITZ强度下数值试件的应力-应变曲线。如图14所示，砂浆和ITZ力学性能的提升会带来数值试件弹性模量和抗拉强度的明显增大，这主要是因为裂缝一般从ITZ区域萌生并沿砂浆内部扩展，因此砂浆和ITZ性能提高会使裂缝在萌生和扩展时消耗更多能量，因而数值试件的弹性模量和抗拉强度逐渐增大。此外，不同骨料和ITZ强度下数值试件的归一化曲线(见图15)表明，随着砂浆和ITZ的弹性模量和抗拉强度的增大，数值试件的延性逐渐降低，脆性逐渐增大。

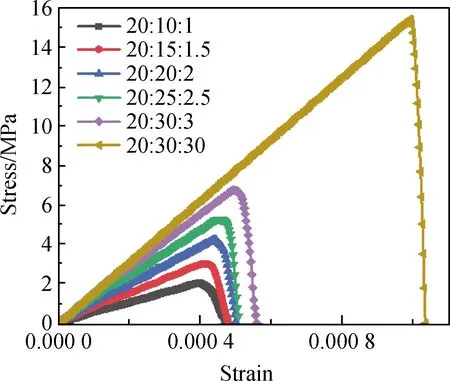
图14 不同骨料和ITZ强度下数值试件的应力-应变曲线

图15 不同骨料和ITZ强度下数值试件的归一化应力-应变曲线

图16为不同骨料和ITZ强度下数值试件的最终断裂形态。如图16中(a)～(c)所示，当fTA∶fTM≥1时，砂浆和ITZ力学性能的提高对混凝土断裂的最终形态基本没有影响，裂缝的萌生和扩展过程也与基准组相似。当fTA∶fTM<1时，ITZ虽仍是体系中的最薄弱区域，但砂浆强度超过骨料强度，骨料成为体系中的次薄弱区域，因此骨料表面出现少量损伤。当fTM∶fTITZ=1时，裂缝从骨料表面萌生并向试件截面尺寸最小的中间部位扩展，数值试件的抗拉强度出现大幅度提升，模拟结果可以与高强混凝土的断裂过程对应[32]。

图16 不同骨料和ITZ强度下数值试件的最终断裂形态

3 结 论

(1)本文所建立的基于近场动力学理论的数值模型可以较好地模拟混凝土在单轴拉伸作用下的力学曲线和断裂形态。但由于键基近场动力学本构关系忽略了砂浆在更小尺度的延性以及二维数值模型不能很好地再现实际三维混凝土试件，因而试件在达到峰值应力之后，力学曲线出现急剧下降趋势，不能很好地再现软化段的曲线。后续研究对键基近场动力学理论进行修正,同时也应结合CT断层扫描、图像识别技术和有限元方法对三维试件进行模型重构，使其能更加精确地预测混凝土的破坏过程,从而对工程结构的材料设计起到指导作用。

(2)粗骨料含量的增加会在混凝土中引入更多的界面过渡区，从而导致抗拉强度降低，但存在阈值。粗骨料含量小于此阈值时，随着粗骨料含量的增加，混凝土的延性降低；粗骨料含量大于此阈值时，界面过渡区萌生了更多的裂缝，因此延性有所提高。此外，不同粗骨料含量下，裂缝的萌生均从界面过渡区开始，沿着骨料边缘或砂浆内部扩展和交叉，最终形成贯通的主裂缝。但粗骨料含量较高时，多个位置的界面过渡区萌生裂缝。

(3)砂浆基体和界面过渡区力学性能的提高会提升混凝土的抗拉强度，同时导致混凝土延性降低，脆性增加。改变骨料、砂浆和界面过渡区的力学参数比值可以较好地模拟出不同类型的混凝土在单轴拉伸荷载下的力学性能和断裂形态。轻骨料混凝土中的轻骨料取代界面过渡区成为体系中较为薄弱的区域，而高强混凝土中截面尺寸最小位置和界面过渡区共同成为体系中较为薄弱的区域，因而轻骨料混凝土和高强混凝土裂缝发展规律与普通混凝土有所不同。