考虑山洪灾害影响的贝叶斯径流模拟方法

梁冀雨，刘曙光，周正正，钟桂辉，方 琦，甄亿位

（同济大学土木工程学院，上海 200092）

山洪灾害是山丘区由降雨、融雪等引起的洪水、泥石流河滑坡灾害的总称[1］，其导致泥沙超量补给现象壅高河道水位产生流量高估现象[2］，使流域出口断面实测径流大于响应流域降雨的清水流量，破坏了流域水量平衡关系，增加了山丘区流域径流模拟结果的输入不确定性。现有水文模型受限于其简化的物理过程、参数估算方法及资料观测条件，在模拟复杂的山丘区小流域水文过程中也会产生来自模型输入、模型参数及模型结构的不确定性[3-4］。在校准水文模型时，上述所有来源的不确定性将集中传递给模型参数[5-6］，降低了径流模拟结果的准确性并造成“异参同效”现象[4］。

贝叶斯方法通过模拟径流的后验分布定量计算其不确定性，提供了较确定性模拟方法更加合理的系统描述，增加了径流模拟结果的可靠性[7-8］。贝叶斯方法通常假定观测径流可分解为由水文模型输出表示的确定性分量及代表残差的随机分量[9］。其中，随机残差的统计模型确定了似然函数及径流预测分布的形式，直接影响着模型参数及贝叶斯径流预测分布估计的鲁棒性和准确性[10］。模拟径流残差具有2个重要统计特征，即时间上的自相关性与异方差性（残差方差随流量增加）[11］。大量的研究证明[6，11-14］，湿润流域径流残差序列的自相关性可使用一阶自回归模型描述，而对于具有明显丰枯变化的流域，则可利用Copula函数建立更加灵活的残差自相关形式[6，11-14］。另一方面，对径流残差的异方差性的处理可分为2种思路：直接处理法和转换方法。直接处理法通过建立残差标准差与协变量（如流量）的函数关系，以此对残差进行标准化处理后，假定残差为零均值、同分布[6，14-17］。转换方法则是在对观测和模拟径流进行函数变换后，直接假定转换后的残差服从均值为零的常方差正态分布[18］。

虽然贝叶斯径流模拟方法能够提升水文模型参数估计的鲁棒性并给出径流预测分布[19］，但是，目前的贝叶斯径流模拟方法皆没有考虑水文过程之外的不确定性来源[20］，特别是忽略了山丘区流域山洪灾害引起的流量放大作用，使其在山丘区流域应用时仍存在以下不足：①假定的残差分布无法描述山洪灾害导致的流量残差极大值，影响了似然函数的合理性；②参数后验估计为补偿山洪灾害导致的观测径流极大值而产生偏差[21］，降低了后验径流预测分布的整体可靠性；③频繁出现的山洪流量极大值增大了模拟残差的方差，令径流预测分布跨度过大、预测精度差。因此，在山洪频发的山丘区流域，贝叶斯径流模拟方法需要进一步优化和改进。

本文以汶川地震后山洪灾害频发的都江堰白沙河流域为研究区域，探究引发山洪灾害的临界雨量，引入线性放大系数修正山洪灾害对径流量的放大作用，耦合一阶自回归残差模型与不同异方差转换函数构建了6种贝叶斯径流模拟方案。选用适用于山区小流域的概念性水文模型GR4J[22］，模拟不同方案下流域出口日径流过程。通过比较不同模拟方案的表现，分析在山区贝叶斯径流模拟中考虑山洪灾害流量放大作用的必要性。

1 研究方法

1.1 模拟残差模型

令t（t=1，2，…，n）时刻山洪灾害流量放大作用导致的附加洪水流量为QF，t，则该时刻的观测流量Q͂t可表示为

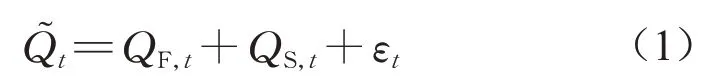
式中：QS，t为t时刻模拟流量；εt为t时刻的原始残差。若假定QF，t是QS，t的线性函数，式（1）可改写为

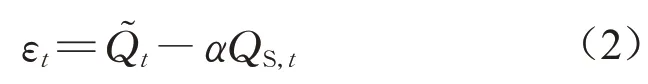
式中：α为模拟流量线性放大系数，α≥1。传统的自相关异方差残差模型不考虑山洪对流量的放大作用，可视为α=1。进一步假定山洪灾害触发条件为前期累积雨量超过临界雨量，有

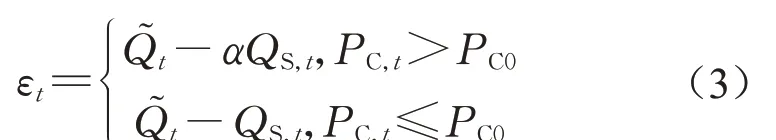
式中：PC，t为t时刻的前期累积雨量；PF为相应的山洪临界雨量。为消除εt的异方差性，在计算残差前，选定转化函数Z将流量正态化，得到正态化残差ηt，即

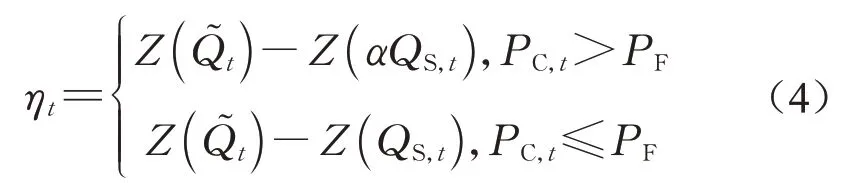
利用一阶自回归模型（AR1）描述ηt的自相关性，有

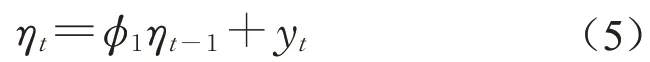
式中：ϕ1为一阶自回归系数；yt为正态化流量残差新息（innovation）。通常假定yt服从均值为零的同方差正态分布[14，17，23］，于是

其中σy为新息yt的标准差。式（1）至式（6）构建了考虑山洪影响的径流量残差模型，其基本假定为流量残差在去除异方差性、自相关性及山洪放大作用后服从均值为零的同方差正态分布。于是，残差模型参数θε={α，ϕ1，θT}，其中θT为转换函数的参数。

1.2 似然函数

令水文模型参数为θH，根据贝叶斯原理，在给定输入资料序列X͂及观测流量序列Q͂时，θH、θε的后验分布可表示为

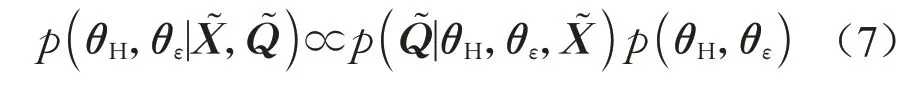
式中：p(θH，θε)为水文、残差模型参数的联合先验分布；p(Q͂|θH，θε，X͂)为似然函数，可看作残差的联合分布，即p(Q͂|θH，θε，X͂)=p(ε(θH，Q͂，X͂)|θε)。若给定异方差转换函数Z，在式（1）至式（6）的假定下，可以得到似然函数

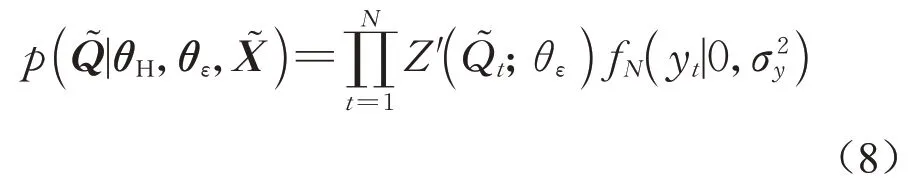
式中：Z′(Q͂t)=dZ(Q͂t)/dQ͂t；fN为正态分布的概率密度函数。本文采用的转换函数及其相应的似然函数表达式见表1，其中A1、A2、A3、λ1、λ2为转换函数参数。若λ2=0，则BC（Box-Cox）转换变为LG（对数）转换。确定转换函数后，似然函数p(Q͂|θH，θε，X͂)通过残差新息构建观测数据与模型、残差参数之间的联系，并以此更新参数的先验分布。

表1 异方差转换函数与似然函数Tab.1 Transformation functions and corresponding likelihood functions

1.3 径流的预测分布

将式（8）代入式（7），利用马尔科夫链蒙特卡罗（MCMC）抽样方法，可以得到水文、残差模型参数的后验分布p(θH，θε|X͂，Q͂)。本文选择Vrugt[24］提出的 DREAM（Differential Evolution Adaptive Metropolis algorithm）算法作为抽样算法，该方法采用自适应随机子空间采样技术（即自适应调整的交叉概率函数），并能在抽样过程中去除无用的马尔可夫链，提高了传统MCMC方法的抽样效率和解的精度，在水文模型的校准方面得到了广泛的应用[24-26］。基于概念水文模型及残差模型参数的后验分布，可以 生 成 模 拟 流 量 的 预 测 分 布Q̂={Q̂r，t；r=1，2，...，Nr，t=1，2，...，n}，其中Nr为采样次数，n为样本容量，其具体步骤如下：

（1）对t=1，2，...，n，从参数后验分布中抽取θH，r、θε，r，对给定的水文模型f，。计算

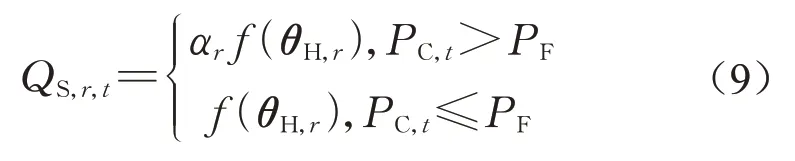
（2）根据式（1）-（6），计算新息标准差σy，r。

（3）生成t时刻的随机残差新息yr，t～N(0，σy，r)。

（4）根据式（5）计算ηr，t。

（5）根据式（4）对转换流量进行逆转换，得到预测流量

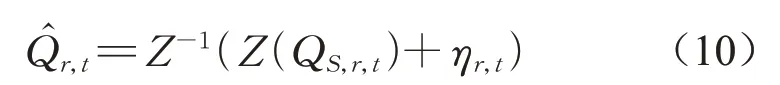
完成Nr次采样后，集合Q̂就是径流的预测分布，其每一个现实Q̂r={Q̂r，t；t=1，2，...，n}可以看作径流过程的一个点估计。于是t时刻径流的后验中位数估计Q̂m，t即为流量预测分布Q̂的横截面Q̂t={Q̂r，t；r=1，2，...，Nr}的中位数，而Q̂t的其余分位数可作为相应置信水平下t时刻预测流量置信区间上下限。

2 研究区域与模拟方案设置

2.1 研究区域

以汶川地震后山洪灾害频发的都江堰市白沙河流域为研究区域，其集水面积为363 km2。该流域位于亚热带湿润季风气候区，降雨充沛，多年平均降雨量约1 134 mm，降雨量年内分配不均匀性显著，5至9月降雨量占全年的80%。同时，降雨是该流域山洪灾害的主要诱发因素[27］。白沙河流域内共有3个雨量站（杨柳坪站、大火地站和虹口站），其中杨柳坪站也是位于流域出口的水文站（见图1）。选用白沙河流域2009—2018年的逐日降雨、蒸发及径流序列进行模拟。

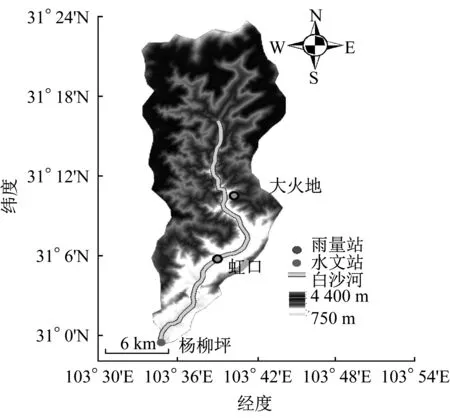
图1 白沙河流域概况Fig.1 Water system,gauging sites,and DEM in the Baisha River Basin

2.2 水文模型

选用Perrin等[22］建立的GR4J概念水文模型，该模型适用于山区小流域的日尺度径流模拟[28］。GR4J模型含有1个产流单元以及1个汇流存储单元，并使用2个单位线方程来描述降雨与径流产生之间的时间间隔，能够模拟流域从降水、蒸散发到产流、汇流的整体过程。模型仅含4个参数，分别为产流单元最大容量S1（mm）、地表水交换系数EX（mm·d-1）、汇 流 单 元 最 大 容 量S2（mm）及 单 位 线 系数U（d）。

2.3 山洪临界雨量

根据白沙河流域内31处山洪沟的监测数据及流域山洪灾害调查报告，白沙河流域内各山洪沟2009—2018年间发生山洪事件天数共347d，包含361次山洪事件。白沙河流域内山洪沟主要分布于上游无人区，少量山洪沟发生洪水时仅会影响河道径流过程，而不会构成严重灾害。

杨柳坪站、大火地站和虹口站3站中，大火地站雨量序列存在缺测情况，为减少缺测资料影响，采用通过等权重的算术平均法估算流域平均逐日面雨量Ṗt，t=1，2，...，n。以山洪当日的前DC日（含当日）累积雨量为判别条件，计算日尺度山洪灾害判别准确率

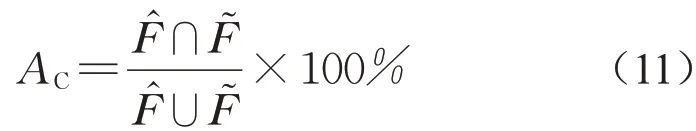
式中：AC为山洪灾害判别准确率；F̂为判别山洪发生的日期集合；F͂为实测山洪发生的日期集合。选取DC=1，2，...，10d，计算流域前期累积面雨量

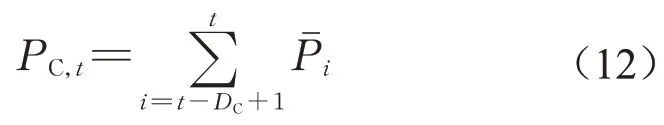
以累积雨量集合PC={PC，t；t=1，2，...，n}的百分位数作为临界雨量PF，令Pe为相应的百分比。根据田述军等[27］的研究，汶川地震后，白沙河流域泥石流临界雨量较震前有所减小，其中DC取1时，临界雨量为51.2 mm，相应Pe值为98.6。针对这一现象，以0.1为步长，取Pe∈[90.0，99.9]，根据不同前期累积日数DC分组，计算山洪灾害判别准确率AC，绘制每组AC样本的箱型图于图2。

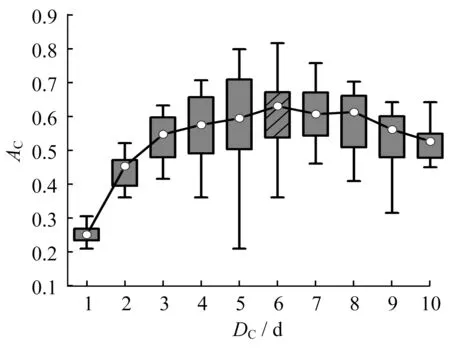
图2 不同累积日数下山洪判别准确率箱型图Fig.2 Box plot of accuracy of flash flood identification

由图2可知，山洪判别准确率AC的均值随前期累积日数DC的增加先增后减，其中当DC取6d时，AC样本具有最高的中位数0.63。选取AC均值最大的DC=5，6，7，8d共4组，绘制AC随Pe的分布于图3。如图所示，当DC=6d，Pe=96.4时，即山洪临界雨量取前6日流域平均雨量18.9mm、累积雨量113.9mm时，AC得到最大值0.81。

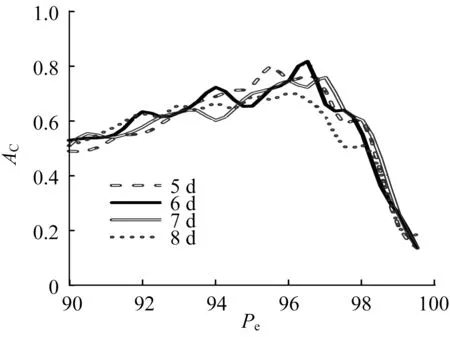
图3 山洪判别准确率随临界雨量百分比分布图Fig.3 Distribution of accuracy of flash flood identification with rainfall percentile

为进一步确定山洪灾害对径流的影响，根据图3中的先验信息，本文选择平均判别准确率最高的DC=6d作为计算前期累积雨量及临界雨量的日数，并将Pe作为残差模型参数，在校准模型时与其余参数一起估计。

2.4 径流模拟方案

选取山洪灾害发生频繁的2013年1月1日至2018年12月31日为模型校准期，以2009年1月1日至2012年12月31日为模型验证期，模型校准、验证期均以其第1年的资料对模型进行预热，调整模型的状态参数S1、S2。为探究本文提出的残差模型对贝叶斯径流模拟方法表现的影响，采用6种模拟方案对白沙河流域杨柳坪站的流量序列进行模拟，模拟方案的设置见表2、表3。

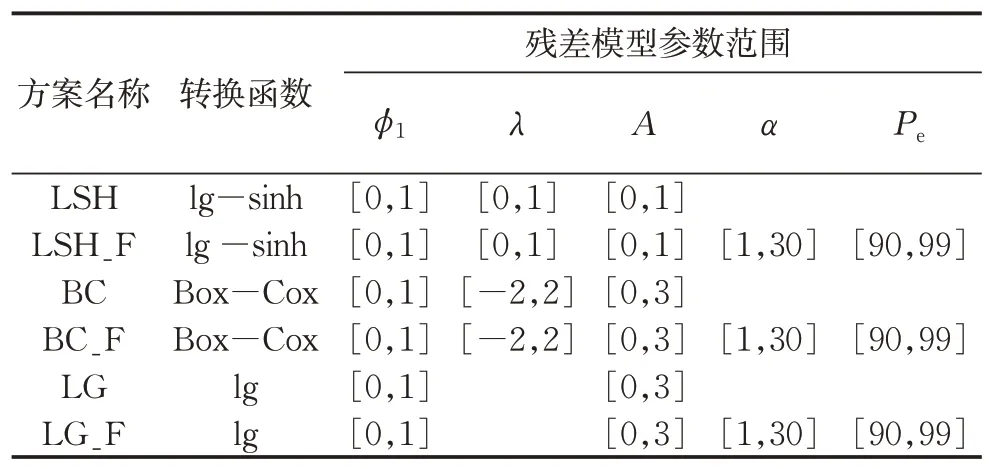
表2 方案设置及残差模型参数范围Tab.2 Simulation schemes and corresponding parameter ranges

表3 GR4J模型参数Tab.3 Parameter ranges of the GR4J model

表2给出了模拟方案的名称，使用的异方差转换函数及残差模型参数范围，以后缀F表示方案采用考虑山洪影响的残差模型。表3给出了GR4J的模型参数取值范围。本文假定所有参数在其取值范围内服从均匀先验分布。同时，设定DREAM算法马尔可夫链数为各方案参数总个数的2倍，参数后验分布样本均取MCMC收敛后的2 000次抽样。

2.5 径流模拟结果评价指标

根据选定的径流模拟方案，为系统性比较不同异方差转换方法及残差模型的模拟表现，选取了不同的统计指标来描述各径流模拟方案的准确性、预测分布可靠性、预测分布精度及残差模型合理性。

2.5.1 模拟准确性

通过径流的后验中位数估计的纳什效率系数（Nash-Sutcliffe model efficiency coefficient）描述径流模拟的准确性，其表达式

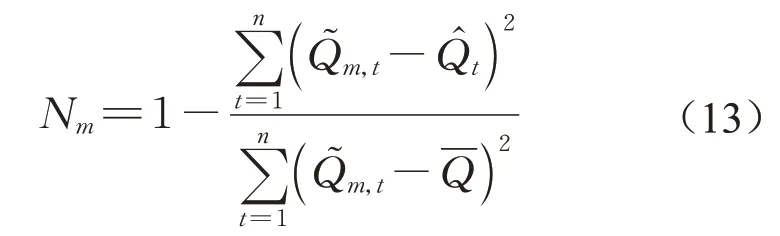
式中：-Q为观测径流序列的平均值。Nm的取值范围为(-∞，1]，越接近1则模拟准确度越高，反之模拟准确度越差。

2.5.2 径流预测分布可靠性

若径流预测分布能捕捉观测资料的分布特性，即径流观测值能看作从径流预测分布中抽取的样本，则称该预测分布是可靠的。采用预测QQ（predictive quantile-quantile plot）图[18，29-30］可 视 化 表征径流预测分布的可靠性，并采用Evin等[17］提出的可靠性指标π对其定量计算，即

2.5.3 径流预测分布精确性

径流预测分布精确性指1.3节中由径流预测分布分位数得到的置信区间宽度，可用精确性指标Pc计算。

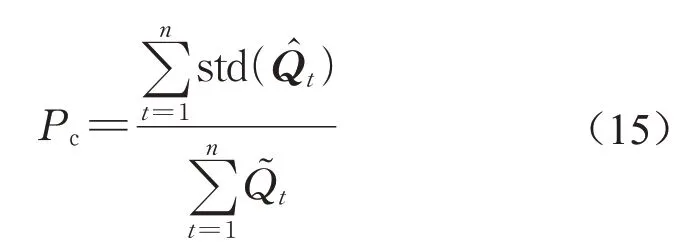
式中：std(Q̂t)为径流预测分布在t时刻的横截面标准差。Pc≥0，Pc值越小，流量预测分布的精度越高、预测置信区间越窄。

3 径流模拟结果分析

3.1 不同方案的径流预测分布

根据表2、表3，利用贝叶斯方法对白沙河流域杨柳坪站的日径流资料进行模拟。不同方案去除模型预热期后的验证期（2010年1月1日至2012年12月31日）径流模拟结果如图4所示。

图4分别展示了考虑山洪灾害影响（图4a、4c、4e）与未考虑山洪影响（图4b、4d、4f）情况下模拟径流分布的95%置信区间与其后验中位数估计，同时，图4a与4b、图4c与4d、图4e与4f分别代表同一种异方差转换函数。

比较图4b、4d、4f可知，在未考虑山洪影响时，3种异方差转换函数中，BC方案低流量模拟的95%置信区间最窄，然而在模拟高流量时出现了较大的不确定性。图5给出了BC、BC_F方案下残差模型参数λ2的后验核密度分布，如图所示，BC方案λ2的后验众数为-1.24，且其后验样本均小于零。图6给出了残差模型后验众数下（λ2=-1.24，A2=0.009，A1=0.017）BC与LG方案的转换流量分布图。如图所示，相比于LG转换，BC转换大幅减小了高低流量差，这弥补了山洪灾害的流量放大作用，减小了残差的整体方差，使BC方案的整体精度在未考虑山洪影响的径流模拟方案中最优。然而，BC方案按式（10）利用逆转换生成流量预测分布时，有预测流量由于A2的后验估计趋于零，当λ2＜0且QS，t较大时，λ2ηt+(QS，t+A2)λ2可能接近零，此时Q̂t→01/λ2，导致流量预测分布频繁采样到不合理的大值，因此出现图4d中的高流量区的高尖峰，降低了高流量区径流预测分布的可靠性和精确性。LSH及LG方案的逆转换函数较为稳定[31］，不易产生不合理的高流量预测，但也无法弥补山洪灾害导致的残差方差增大，导致其低流量区域的置信区间较宽。

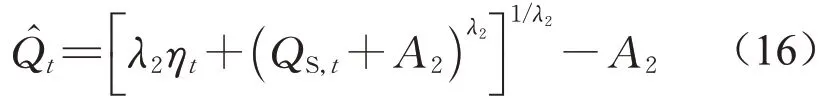
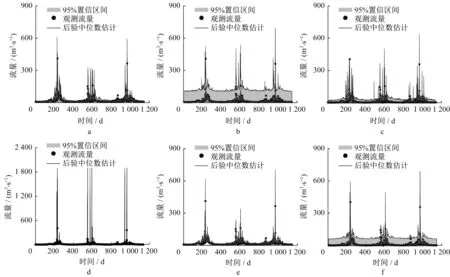
图4 杨柳坪站验证期不同方案径流模拟结果Fig.4 Simulation performance of different schemes in validation period

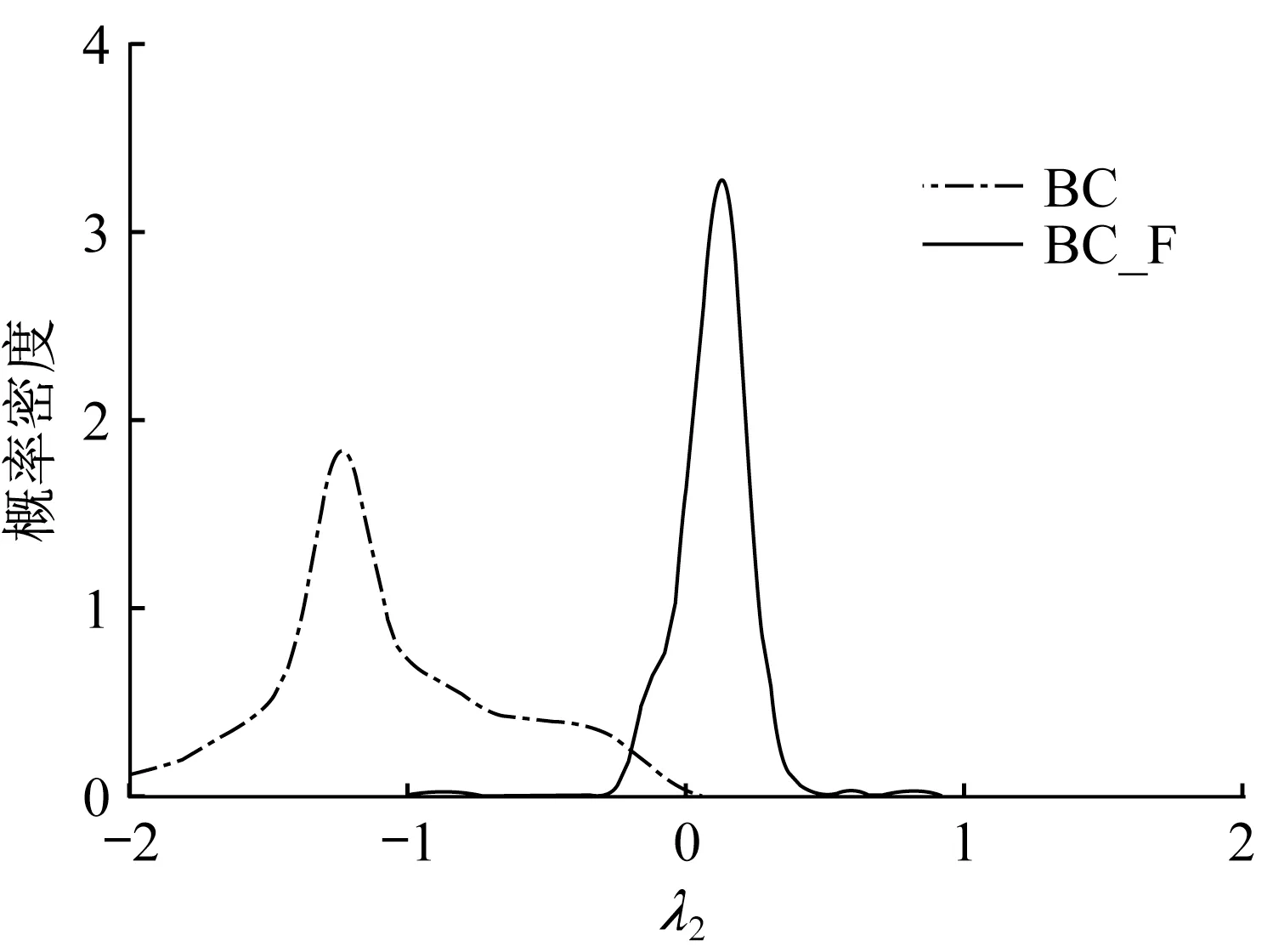
图5 λ2后验核密度分布Fig.5 Posterior kernel density ofλ2

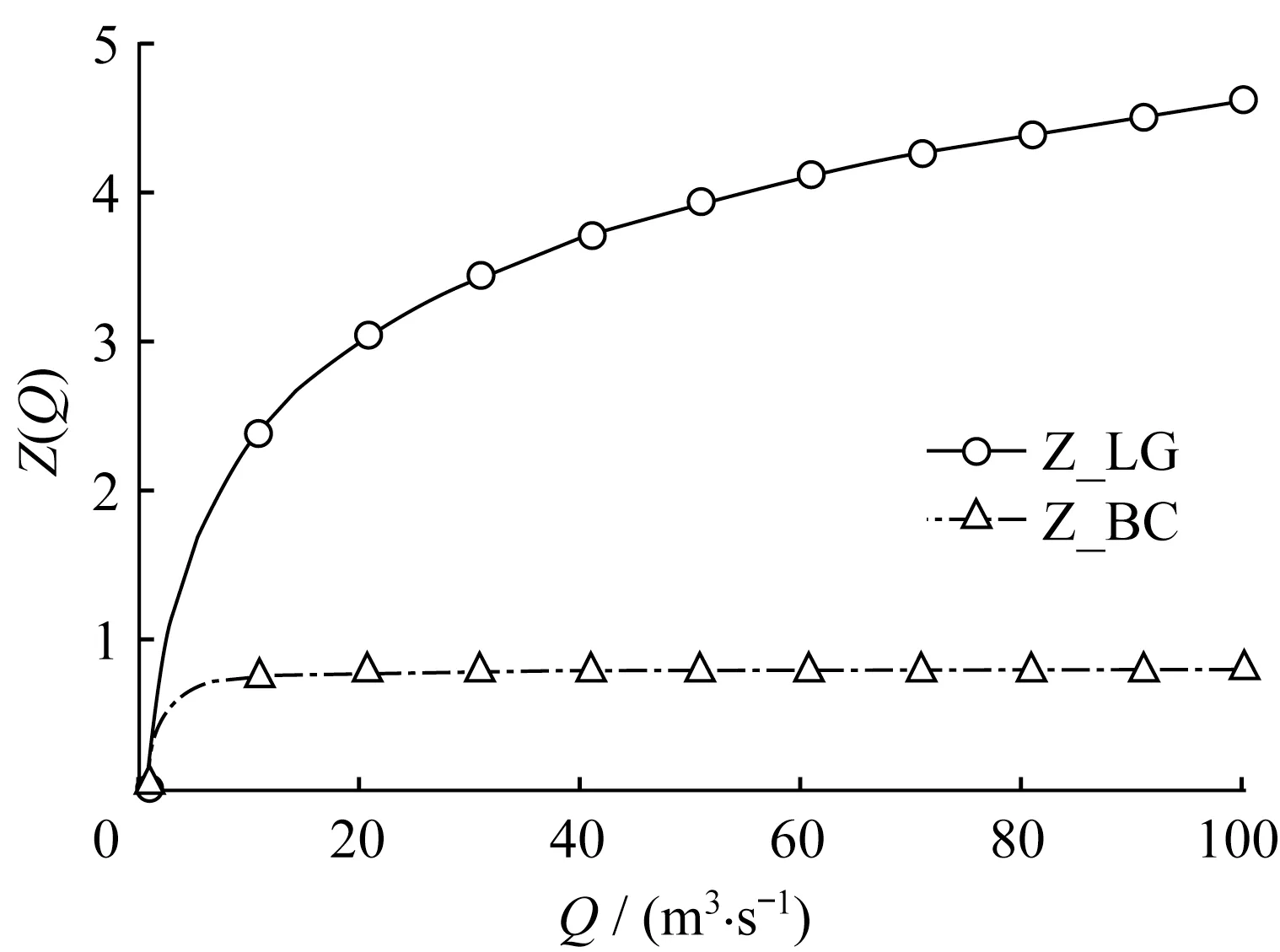
图6 LG、BC方案转换流量对比Fig.6 Transformed runoff of LG and BC scheme

对比图4a、4c、4e与图4b、4d、4f，易见考虑山洪灾害对流量的放大作用后，模拟径流的95%置信区间宽度皆明显减小。其中，BC_F方案参数λ2的后验众数为0.12（图5），仅19%的λ2后验样本小于零，显著减小了流量预测分布采样到异常值的概率，增加了BC逆转换下高流量径流预测分布的可靠性和精确性。

除转换函数本身的性质外，对应于残差标准差的残差新息标准差σy对流量预测分布的精确性也有着直接影响，较大的σy值对应较宽的径流预测分布及较大的预测不确定性。表4给出了6种方案下σy的后验样本的5%分位数、中位数及95%分位数。根据表4，采用考虑山洪影响的残差模型后，LSH、BC、LG这3种方案的σy中位数分别减小84%、25%、23%，σy的90%置信区间宽度分别减小15%、90%、17%。

表4 不同方案后验σy分位数表Tab.4 Quantiles of posterior distribution ofσy

表5列举了6种模拟方案的准确性指标Nm、可靠性指标π及精确性指标Pc。由表5可知，与前述一致，未考虑山洪影响时，BC方案在径流预测分布精确性指标Pc及准确性指标Nm上表现最优。综合考虑全部6种方案后，模拟准确性最优方案为LSH_F，而预测分布可靠性及精确性的最优方案皆为LG_F。

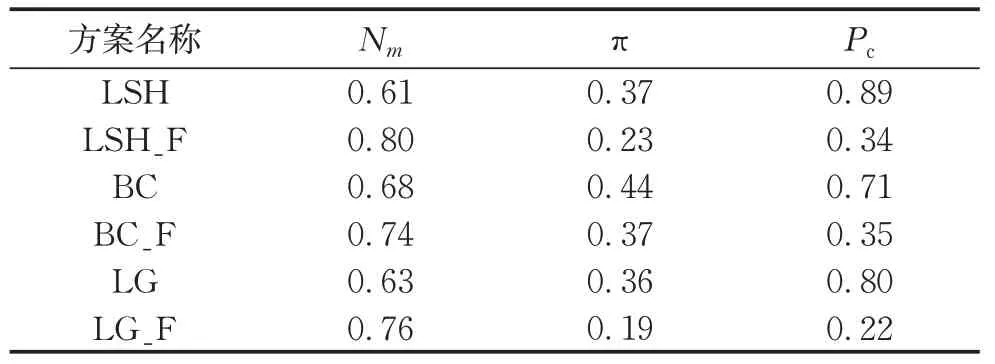
表5 不同方案模拟结果评价指标Tab.5 Performance metrics of different schemes

值得注意的是，除最优方案外，亦可发现在采用考虑山洪影响的残差模型后，径流模拟结果评价指标都有所改进，其中，Nm平均提升19%，π平均降低32%，Pc平均降低62%，而对于不同的异方差转换函数，LG方案3项评价指标平均提升45%，LSH及BC方案分别平均提升43%和26%。

3.2 残差新息的后验分布

以LG方案为例，分别绘制LG、LG_F方案标准化残差新息v的直方图于图7、图8。如图7所示，与标准正态分布相比，LG方案的标准化残差新息分布呈较强的正偏态，右侧有长尾并有较大的峰度。相较之下，图8中LG_F方案的标准化残差新息与标准正态分布更为一致。为进一步比较，将LG和LG_F方案下v的均值、偏态系数及峰度系数列于表6。

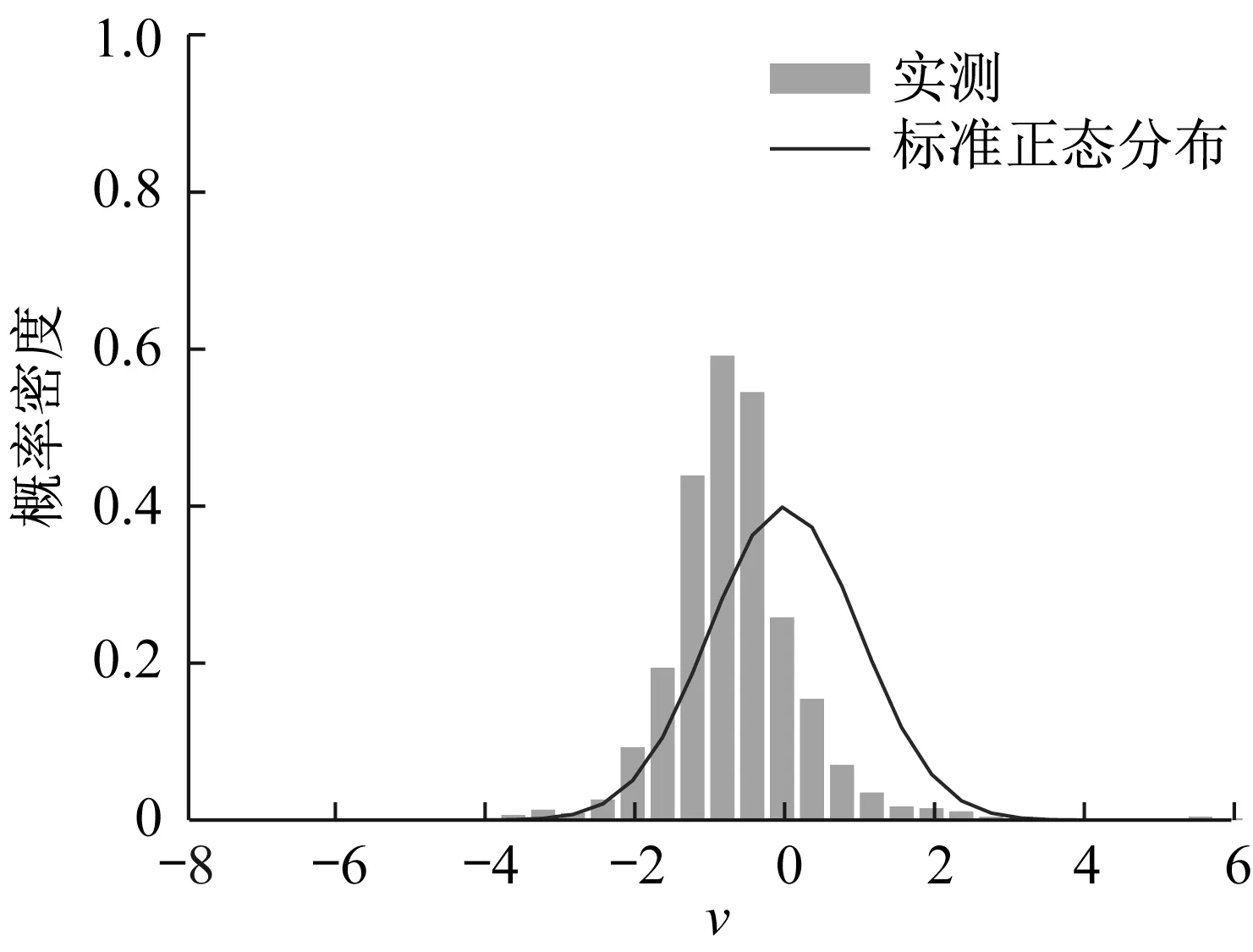
图7 LG方案标准化残差新息直方图Fig.7 Histogram of standardized innovation of LG scheme

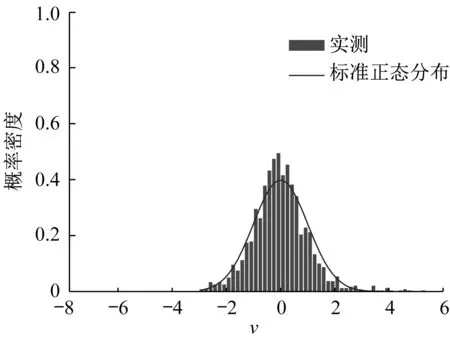
图8 LG_F方案标准化残差新息直方图Fig.8 Histogram of standardized innovation of LG_F scheme

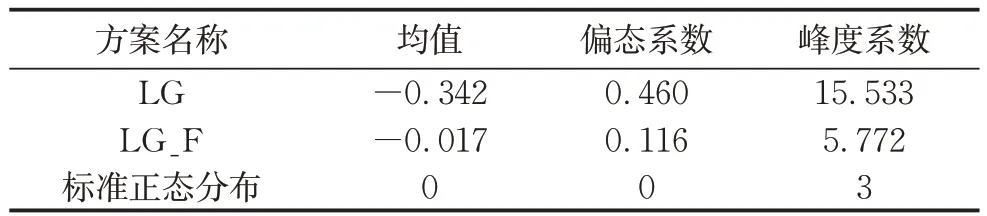
表6 考虑山洪灾害影响前后标准化残差新息v统计参数Tab.6 Statistics of standardized innovation of LG and LG_F schemes

由表6可知，相较于LG方案，LG_F方案下v的统计参数更接近残差模型所假定的标准正态分布的统计参数。由于2种方案中v的标准差均为1，因此具有更大峰度系数的LG方案中v包含更多的特大值，根据式（3）-（6）可知，某些时间点的模拟径流远小于观测流量。分别记LG方案v中较大的前5%、3%为v5及v3。v5与山洪灾害发生时间重合的天数占v5总数的65%，v3相应重合比例为83%，表明v出现特大值与山洪灾害发生具有较强的相关性。而这些特大值也是LG方案下v的分布出现较强正偏性的主要原因。同时，MCMC参数估计方法过多关注这些特大值[32］，导致参数的后验估计使模型模拟径流QS整体偏大，造成低流量区域QS频繁大于观测流量Q͂，使LG方案下v的均值小于零。

另一方面，LG_F方案通过流量线性放大系数α放大山洪灾害发生时的模拟径流QS，减小了这些时间点上QS与观测流量Q͂的偏差；LG_F方案下v5、v3的均值较LG方案分别降低39%、57%。v的特大值的下降进一步提升了MCMC参数估计的准确性，降低的低流量区域负残差的出现概率使v的均值由-0.342增至-0.017。综上，考虑山洪影响的残差模型通过识别并修正山洪灾害导致的转换残差特大值，使其更接近假定的同方差正态分布，LSH与BC方案下得到的结论与LG方案相似。

3.3 山洪修正参数的后验分析

相较于未考虑山洪灾害影响的自相关异方差残差模型，本文通过引入参数Pe、α识别并修正山洪灾害对流量的放大作用。图9、图10给出了3种考虑山洪影响的残差模型参数Pe、α的后验核密度分布。

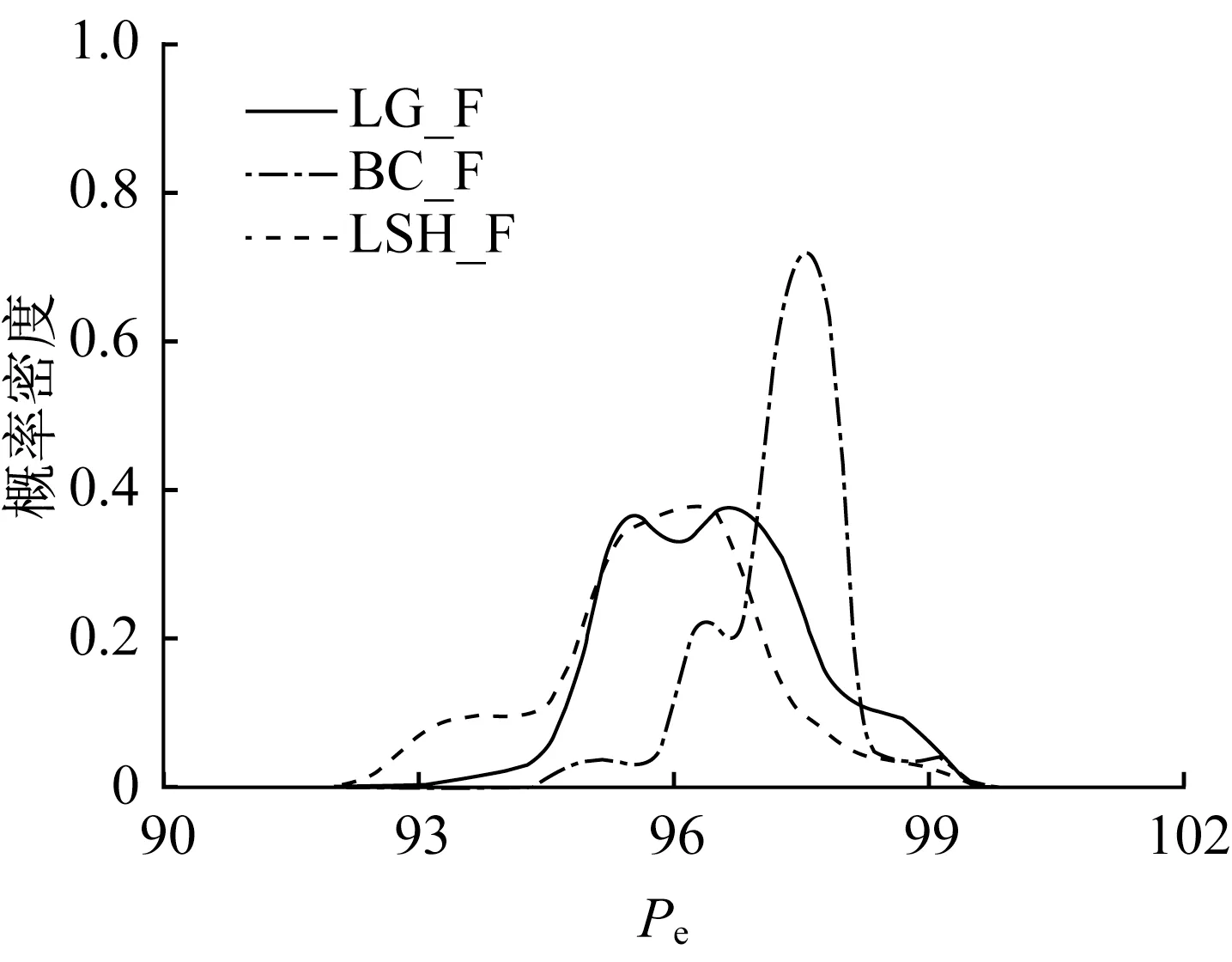
图9 各方案P e后验核密度分布Fig.9 Posterior kernel density of P e

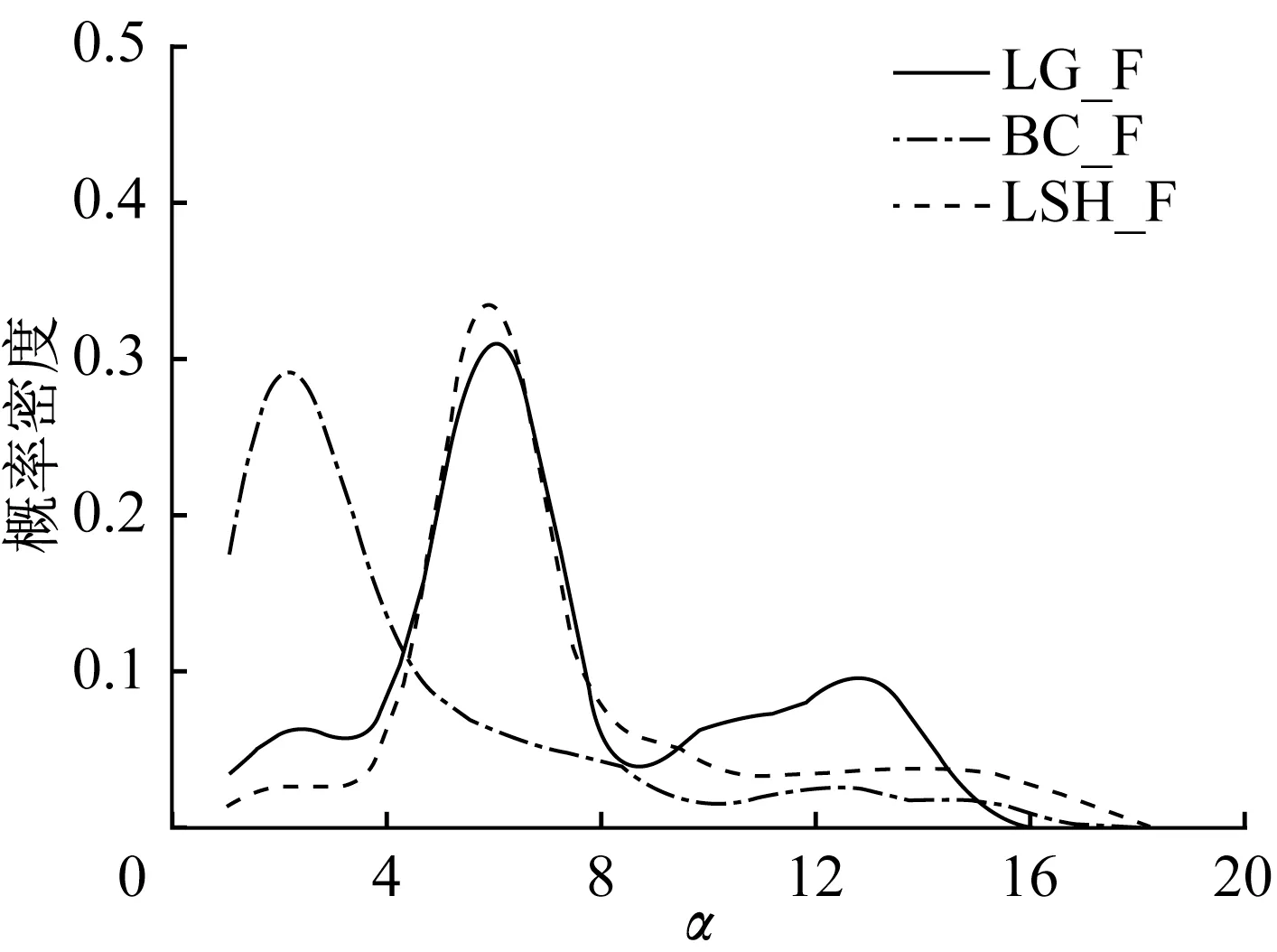
图10 LG_F方案α后验核密度分布Fig.10 Posterior kernel density ofα

根据图9，LG_F方案Pe的后验分布集中于95至98之间，其最大后验估计为96.5，对应的前6日临界累积雨量为115.1mm。值得注意的是，该雨量并非传统意义上的山洪临界雨量，其含义是，当前期雨量超过该值时，流域响应径流发生明显增大，需要进行修正。因此，该雨量应称为“流量修正临界雨量”。同时，根据图10，LG_F方案α的后验众数为6.0，在式（3）的假定下，即判断山洪发生时，径流量将被放大6倍，这一结果与胡凯衡等[33］得到的非线性流量修正系数结果相近。

LSH_F方案Pe、α的后验分布与LG_F方案相似，而BC_F方案的Pe后验众数为97.7，判别验证山洪灾害发生的日数较LG_F、LSH_F方案减少约14d，山洪灾害识别准确率AC为0.59。同时，BC_F方案α的后验众数为2.8明显小于LG_F、LSH_F方案。造成这一差异的一个可能原因是BC转换函数Z2（表1）在λ2较小的情况下，减小了高流量观测值与模拟值，因此平缓了山洪灾害导致的较大模拟残差与普通残差的区别，使残差模型无法完全识别、修正某些场次的模拟残差。同时，这种残差平缓效应也使得参数α的后验估计偏小。

4 结论

山洪灾害壅高河道水位带来的流量放大作用影响了贝叶斯径流模拟方法在山丘区流域的表现。以汶川地震后山洪灾害频发的都江堰白沙河流域为研究区域，基于引发流域山洪灾害的临界雨量，引入线性放大系数修正山洪灾害对流量的放大作用，耦合一阶自回归残差模型与不同异方差转换函数构建了6种贝叶斯径流模拟方案，利用GR4J模型模拟不同方案下流域出口日径流过程，得到如下主要结论：识别并修正山洪灾害的流量放大作用后，①山丘区流域径流残差新息更接近残差模型假定的同方差正态分布；②贝叶斯径流模拟表现明显提升，其中准确性、可靠性及精确性指标平均提升19%、32%、62%；③不同异方差转换函数中，LG转换得到了最优的径流预测分布可靠性及精确性，log-sinh转换得到了径流过程的最优后验中位数估计，而BC转换受限于其转换函数特性，对山洪灾害的识别及修正效果较差，径流模拟表现的提升有限。

提出的考虑山洪影响的贝叶斯径流模拟方法理论基础扎实，修正了山洪灾害对山丘区流域径流量的放大作用，优化了径流模拟结果，可在汶川地震后山洪频发的山丘区流域推广应用，为径流预报提供更为准确的科学依据。同时，为进一步提升山丘区贝叶斯径流模拟的表现，除临界雨量、线性放大系数外，更加高效、准确的山洪灾害识别及流量修正方法值得继续深入研究。

作者贡献声明：

梁冀雨：数据收集整理、模型脚本编写、模拟结果分析及论文撰写。

刘曙光：提供研究思路及设计模拟实验方案。

周正正：数据校核及论文修订

钟桂辉：数据校核及论文修订

方 琦：数据校核及论文修订

甄亿位：数据校核及论文修订。