广义微极近场动力学模型及三维断裂行为模拟

陈希卓，禹海涛，朱建波，刘建锋

（1.同济大学土木工程学院，上海 200092；2.四川大学深地科学与工程教育部重点实验室，四川成都 610065；3.同济大学土木工程防灾国家重点实验室，上海 200092；4.深圳大学土木与交通工程学院，广东深圳 518061）

材料的裂纹扩展和破坏问题一直都是固体力学研究和工程领域面临的关键难题[1］。目前学者们已经提出了众多的力学模型和数值方法来模拟固体材料断裂过程，如扩展有限元[2-3］、内聚力模型[4-5］和边界元方法[6］等。然而，这些方法都需要引入特定的附加函数和断裂准则来描述不连续行为，无法有效模拟裂纹的自发萌生和扩展过程[7-8］。此外，由于传统的数值方法大都是基于连续性假设，因此在处理断裂等非连续行为时必须面对导数奇异性问题，从本质上难以准确模拟破坏问题。

为了解决这一难题，Silling[7］提出了近场动力学（PD）理论，采用考虑非局部作用的积分模型代替传统理论的微分模型，有效避免了传统连续介质力学方法在处理断裂行为时的导数奇异性问题。该方法实现了由连续到不连续、微观到宏观力学作用的统一描述，尤其在分析裂纹扩展等非连续力学问题时具有显著优势。近些年来，PD方法已逐渐成为计算力学及相关领域的关注热点，其主要可以分为键基和态基2种模型[8］。对比态基近场动力学模型，键基模型的计算量更小，同时不存在零能模态的问题，因此广泛应用于岩石和混凝土等准脆性材料的断裂行为模拟。朱其志等[9］运用近场动力学方法对含有预制裂隙的岩石类材料试件的单轴压缩试验进行数值模拟，分析了不同裂隙倾角对裂纹扩展模式的影响。Rabczuk和Ren[10］基于带对偶-近场作用的近场动力学（DHPD）模型实现了岩石内部裂纹扩展和准脆性断裂过程模拟。Wang等[11］发展了一种新型共轭键基模型，模拟了单轴压缩条件下预先含有裂隙的岩石试样中裂隙的分叉和合并行为，揭示了单轴压缩条件下岩石的裂纹扩展机制。Gerstle等[12］提出了微极近场动力学（MPPD）模型，采用Euler-Bernoulli梁模型描述物质点之间的相互作用，有效模拟了混凝土构件失稳和破坏过程。Diana等[13］运用微极近场动力学分析了砂岩在三点弯曲试验中的力学特性，有效捕捉到了试件的I型和混合型断裂过程。

上述近场动力学模型在准脆性材料断裂过程的模拟中均取得了不错的效果，但其主要还是集中于二维断裂问题。实际上，准脆性材料在三维条件下会出现更复杂的体破坏现象，裂纹的空间扩展模式也会呈现较大差别[14］。而传统的微极近场动力学模型对复杂条件下材料三维断裂行为的模拟精度不高，主要原因在于其无法保证不均匀应变场下近场动力学和传统连续介质力学的能量一致性以及缺乏相应的三维断裂准则。

本文提出一种广义微极近场动力学（GMPD）模型，在传统微极近场动力学（MPPD）模型基础上进一步考虑三维状态下键的轴向变形、切向变形、相对转角之间的耦联作用，可有效提高三维断裂问题的模拟精度。通过引入对应于键拉、剪、弯力学行为的3种近场动力学参数，以保证复杂荷载条件下近场动力学与传统连续介质力学应变能的一致性。另外建立基于能量的新型断裂准则，旨在实现准脆性材料的三维断裂过程模拟与准确预测。

1 广义微极近场动力学模型

基于非局部作用的思想，近场动力学理论假定物体内的任一物质点位置矢量xi与其周围一定区域Hx内的其他任意物质点位置矢量xj之间存在相互作用，这种作用可以理解为键，而力通过键在物质点间进行传递。为了消除泊松比的限制，微极近场动力学模型引入了Euler-Bernoulli梁模型来描述物质点之间的相互作用，但是该模型忽略了键的剪切变形和转动惯量，无法对复杂加载条件下的力学行为尤其是三维断裂问题进行准确模拟。鉴于此，提出了一种广义微极近场动力学模型，引入了Timoshenko梁来模拟物质点间的相互作用，进一步提高模型的模拟精度与适用性。

1.1 控制方程

基于Timoshenko梁理论，xi在t时刻的运动控制方程可表示为

式中：ρ为物质密度；u（xi，t）为xi的位移向量；Hx为xi的作用域；f为xi和xj间的相互作用力；θi和θj分别为xi和xj的相对转角；b（xi，t）为作用于xi上的外部体力；I为转动惯量；A为键的截面面积；m为xi和xj间的弯矩相互作用；n（xi，t）为作用于xi上的外部弯矩；η和ξ分别为物质点间的相对位置向量和相对位移向量，可表示为

基于局部坐标系，键的对偶力函数f与对偶力矩m可分解为

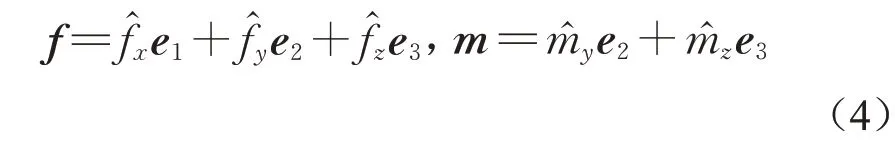
式中：e1、e2和e3分别为局部坐标系下沿x、y和z轴的单位向量。

引入分别对应拉伸、剪切和弯曲刚度的键参数CN、Cθ和CM，并结合Timoshenko梁单元受力方程，可得到单根键上的力和弯矩在局部三维坐标系下的表达为

1.2 应变能与键参数

通过对键的微势能w进行域内的积分，可以得到该模型的应变能密度WPD。

式中：d为局部坐标系下键的变形分量的统一表达；K为键的刚度矩阵。

建立如图1所示的球面坐标系OX′Y′Z′，三维条件下GMPD模型的应变能密度可以进一步表示为

图1 球坐标系下键的变形构型Fig.1 A bond with the deformed configuration in global spherical coordinate system

式中：δ为作用域的半径大小；α为键与球坐标系中z′轴的夹角；β为键在Ox′y′平面的投影与x′轴的夹角。

基于近场动力学应变能WPD和传统连续介质力学应变能WCM的等价关系可以得到三维条件下键参数的表达为

将式（5）和式（6）代入式（8），并通过局部到整体的坐标变换可以得到GMPD模型的应变能密度表达，如式（9）：

而传统连续介质力学的应变能密度WCM为

1.3 断裂准则

为了有效捕捉准脆性材料的破坏过程，提出了一种基于能量的新型键基断裂准则。在该模型中，假定当穿越某一平面的键AB全部断开时，物质点A的域内形成相应的宏观裂纹，如图2所示，因此材料的平面断裂能应等于所有断开键的应变能总和，如式（13）：

图2 断裂演化过程示意Fig.2 Evaluation of fracture energy

展开求解式（13），可以得到键的轴向变形、剪切变形以及相对转角的限值s0、γ0和θ0，分别为

当键的变形达到相应的峰值后会自动断开，即键两端的物质点不再产生相互作用，从而在宏观上形成裂纹。这里引入标量函数μ（xi，xj，t）描述物质点间键是否发生破坏，如式（15）：

基于上述标量函数，xi的损伤度d（xi，t）可以表示为

损伤度为0，代表物质点完全无损伤；损伤度为1，表明物质点周围的键完全断裂。

2 数值实现

为了求解GMPD模型中的控制方程，首先在空间上对求解域进行离散化处理，在这里将求解域离散成物质点，每个物质点都占据一定空间体积且拥有一定物理性质，离散后的运动控制方程可以表示为

式中：ΔVj为空间离散化处理后xi域内的xj所占据的空间体积。

采用显示中心差分方法求解上述控制方程，用有限差分近似代替位移对时间的导数，可以得到物质点的加速度和速度的表达为

将式（19）代入式（17），可以得到位移的递推求解格式为

将式（20）代入式（18），可以得到转角的递推求解格式为

该模型的边界条件主要包括位移边界和力边界。其中外力P（x）是通过转化为体力b（x）作用于最外层的物质点Lr上，如图3所示，其中Δ为物质点间距。具体的转换关系为

位移边界主要是作用于物质点外的虚拟边界上，通过虚拟边界层带动内部物质点一起运动。如图3所示，虚拟边界的尺寸和作用域半径δ一致。

图3 力和位移边界条件Fig.3 Force and displacement boundary conditions

GMPD模型的完整数值求解流程如图4所示。

图4 数值求解流程Fig.4 Computational flowchart of proposed model

3 三维断裂模拟

为了说明GMPD模型对于三维断裂问题的适用性，基于该模型模拟单轴压缩条件下准脆性材料试件的准静态破坏过程，并通过与传统微极模型以及文献中已有试验结果进行对比来验证模型的有效性。

选取含单条初始裂隙的立方体试件为对象，如图5所示。基于文献[14］的试验参数，试件的弹性模量取E=3.81×109Pa，密度ρ=1.21g·cm-3，泊松比v=0.4，表面断裂能G0=452N·m-1，初始裂纹半径a=5mm，裂纹倾角α=30°，在两侧施加速率为2mm·min-1的轴向压缩荷载。在近场动力学模拟中，假定试件为均匀和各向同性的，采用间距Δ=0.001m的物质点对试件进行离散，作用域的大小取δ=3Δ。

图5 压缩荷载下含初始裂隙试件[14］（单位：mm）Fig.5 Single flawed samples under uniaxial compression[14](unit:mm)

图6为加载过程中本模型预测的试件裂纹扩展状态。由图6a可知，预制裂纹边缘最先开始发生破坏并逐渐形成翼型裂纹。在翼型裂纹不断延伸的同时，反翼型裂纹（方向和翼型裂纹相反的拉伸裂纹）也开始在预制裂纹尖端萌生并扩展（见图6b、图6c）。随着荷载的逐渐增加，翼型裂纹边缘产生了次生裂纹，裂纹沿水平方向延伸至试件边缘造成材料破坏（见图6d）。本文模拟所得裂纹类型及其扩展路径与试验结果[14］基本一致（如图7），有效捕捉到了三维空 间内产生的翼型裂纹、反翼型裂纹以及次生裂纹。

图6 加载过程中GMPD模型预测的裂纹扩展过程Fig.6 Predicted crack propagation in specimen under axial compression

图7 压缩荷载下试验观测的试件裂纹扩展过程[14］Fig.7 Experimental observation of crack development of specimen under axial compression[14]

为了进一步说明二维断裂与三维断裂模拟的差异性，图8给出了相同荷载作用下传统MPPD模型预测的二维裂纹的扩展模式。

由图8可见，二维裂纹发展主要以翼型裂纹为主，且扩展方向与荷载施加方向基本一致。进而，通过与图6对比可以发现：三维条件下裂纹的扩展过程更为复杂，会演化生成更多不同类型的裂纹，从而进一步证明本文所建立的GMPD模型在模拟准脆性材料三维裂纹扩展问题方面的准确性和优越性。

图8 传统MPPD模型预测的最终裂纹扩展模式Fig.8 Final growth path obtained from the original MPPD model

4 结语

提出了一种广义微极近场动力学（GMPD）模型，可以有效模拟准脆性材料的三维断裂行为。模型采用Timoshenko梁来模拟物质点间的相互作用，从而充分考虑键在三维受力条件下的轴向变形、切向变形、相对转角以及三者之间的耦合作用。引入了可分别表征键的拉伸、剪切以及弯曲刚度的3个键参数，实现了任意变形场下近场动力学和传统连续介质力学的能量一致。同时基于能量提出了一种新型断裂准则，给出了键轴向变形、切向变形以及相对转角的临界值，实现准脆性材料的三维破坏模拟。

基于所提出的GMPD模型模拟了单轴压缩荷载作用下试件的三维破坏过程，结果表明该模型可以有效捕捉复杂荷载条件下不同类型裂纹的萌生和扩展，包括翼型裂纹、反翼型裂纹以及次生裂纹的发展过程。通过模型预测结果与试验结果对比，进一步验证了模型的准确性，表明本模型可以有效应用于准脆性材料的三维断裂行为模拟，可为工程破坏问题提供分析依据。

作者贡献声明：

陈希卓：模型构建、数据分析呈现及论文撰写。

禹海涛：项目负责人、论文构思、指导模型构建及数据分析，论文修改。

朱建波：论文修改，提供试验数据。

刘建锋：论文修改。