扩展键基近场动力学的几何非线性扩展
2022-05-13朱其志李惟简曹亚军
朱其志,李惟简,尤 涛,曹亚军
(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京 210098;2.河海大学土木与交通学院,江苏南京 210098)
传统的基于经典连续介质力学的数值方法,如有限元法,能够通过迭代求解线性方程组较好地处理线性连续问题。然而在处理非连续问题时,由于难以定义非连续界面的应力导数,所以这类方法的数学模型在裂纹开展处存在一定的缺陷。为了解决这个问题,学者们提出了多种替代性的数值方法,其中近场动力学方法因其非局部的键力描述[1]以及无网格离散的特性[2]而备受关注。该方法通过对键力密度积分的形式重构控制方程,从而能够有效处理位移不连续问题。通过近些年的发展,近场动力学方法已经具备可靠的弹性预测能力和断裂预测能力[3-5],在此基础上,许多学者开展了大量的研究使其能够更加精确地捕捉断裂响应[6-8]。
在原始的键基近场动力学公式[1]中,2个相互作用的粒子在法线方向上只有成对的中心力,导致模型的泊松比不能自由定义。为了克服固定泊松比的限制,一些学者在本构关系上进行了相应的扩展[9-13],其中应用最广泛的是态基近场动力学模型。该模型根据经典弹性力学思路将近场动力学变形态分解成净体积变化部分以及剩余部分。Madenci等[14]通过应变能密度中偏量部分与等效应力的关系提出了一种基于态基近场动力学的塑性模型,但是其相关研究[15-18]受限于冯米塞斯屈服准则。同时,与常规态基近场动力学一样,其测量体积应变的方式是基于小变形假设条件,所以在进行几何非线性分析时需进行特殊处理[19-20]。
Zhu等[21]和Li等[22]开发的扩展键基近场动力学模型(XPD)将剪切应变项引入原始公式,解决了泊松比的限制问题,并且建立了宏观弹性常数与微观键模量之间的关系。基于局部应变的数值实现方法可以准确描述二维、三维任意泊松比的各向同性材料模型的线性弹性行为。在该扩展模型中,通过计算小变形理论下的“局部应变”来确定键剪应变效应,其中假设材料粒子的位移远小于物体的任何相关尺寸,因此其几何形状和空间各点处材料的本构关系不随变形而改变。然而,这种近似对于薄壁或细长结构,例如梁、板和壳这类容易受到显著旋转和位移影响的结构,结果不可靠。
对于细长结构或薄壁结构,Diyaroglu等[23]引入了近场动力学模型来预测梁的弯曲和横向剪切变形。O’Grady等[24]引入了非常规态基近场动力学模型来分析基于基尔霍夫洛夫理论的弯曲变形平板。Nguyen等[25-26]针对壳结构开发了一种常规态基近场动力学模型,该模型可以用于预测加筋结构的损坏。在这些薄的柔性体中观察到大位移和大旋转是很常见的,但是Nguyen等[19]提到上述近场动力学(PD)模型都基于线性分析中的小变形假设。
对于某种数值方法,将其从小变形预测延伸至大变形分析,是对其应用范围的重要扩展。它需要考虑结构的几何非线性特性,这也是众多工程应用中需要解决的关键问题。因此学者们发展了多种数值方法,如无网格方法[27-29]、格子方法[30]、大变形边界元方法[31-32]等。其中无网格法不依赖网格划分的质量,在处理流体大变形问题中具有独特的优势,然而其数值精度较难提高并且施加本质边界条件比较困难;格子方法类似于将材料离散为有限数量的颗粒,颗粒间通过直接接触相互作用,虽然其在应对材料断裂问题时有一定优势,但格子法模拟材料的力学特性严重依赖于颗粒的排布方式,从而影响了该方法的普适性。大变形有限元方法[33-36]由于其在连续变形预测方面的成熟度和可靠性,已被一些基准研究用作参考方法,但有限元方法的网格依赖性以及在处理非连续问题时的局限性也限制了其应用的范围。
本文主要考虑几何非线性影响,旨在将扩展键基近场动力学模型应用于大变形问题。考虑到连续体的变形构型与未变形构型存在显著差异,采用变形梯度张量来表示从初始构型到当前构型的映射。变形梯度张量可以表示为位移场相对于初始坐标的导数,因此利用Li等[22]提出的拟合方法计算局部位移函数,从而得到局部变形梯度场。通过极坐标分解,可以将变形梯度张量分解为2个独立的运动过程即刚性旋转和变形,从而正确计算出每个扩展键的变形部分。
1 扩展键基近场动力学
在经典近场动力学模型中,局部平衡方程被描述为力密度函数f(X)的积分,其中属于彼此近场域的2个物质点沿着连接键的方向相互作用,如图1。对于某一物质点(所在位置记为X,HX代表物质点X的近场域范围),它在时刻t的运动平衡方程为
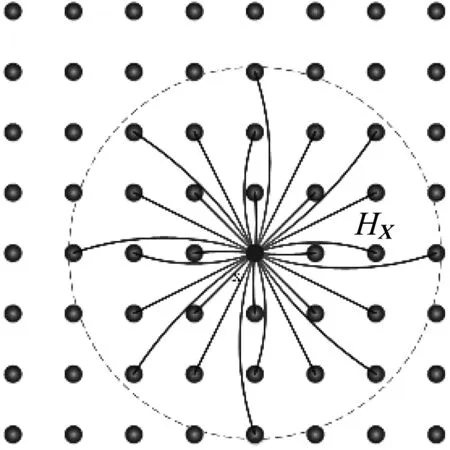
图1 物质点分布以及近场域示意Fig.1 Material distribution and definition of horizon

式中:ρ为材料密度;ü为加速度向量;b(X,t)为体力密度;VX′为物质点X′所占体积。
取2个位置不同且相互作用的物质点,X和X′分别为其位置坐标,则其相对位置向量可以定义为

假设两物质点在时刻t时分别产生了位移u(X,t)以及u(X′,t),那么这两点的相对位移向量η可以写成

局部键本构关系可以描述为

式中:C为键刚度张量。文献[1]在键的拉压变形以外引入了一种局部剪切机制,将键刚度张量表示为

式中:ξ=‖ξ‖,n=ξ/ξ表示键方向向量;c和κ分别表示键在法向以及切向方向的刚度,可以直接由材料的基本参数求得(杨氏模量E和泊松比ν)。近场域H的大小由δ来表示。
在三维模型中,有

1.1 有限变形理论下的键变形计算方法
使用X标记未变形构型中某一位置,x(X,t)表示运动变形后构型中对应位置,变形梯度张量F是变形后向量的每个分量对于未变形向量的每个分量的导数

式中:δij为克罗内克符号。
极分解定理表明,任何二阶张量都可以分解为纯旋转和对称张量的乘积,因此固体的旋转和变形可以分解为

式中:R和S分别为旋转张量以及右伸长张量。
经过刚性旋转后的键相对位置向量可表示为

由几何视图(图2)可知,有效相对位移为
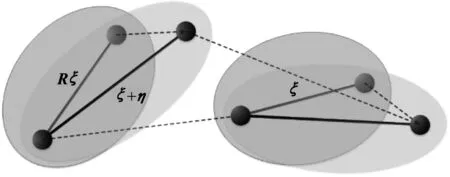
图2 键位移、旋转、变形示意Fig.2 Bond displacement,rotation and deformation

则键的实际变形量可由式(13)、式(14)计算得到:

1.2 变形梯度张量的拟合
局部位移函数使用局部的物质点位移来拟合,此位移函数可近似为一多元线性函数u。

式中:a为系数矩阵的组合;b为刚体位移。从而有

应用最小二乘法最小化每个位移分量的残差总和,得到

式中:A为系数a组成的矩阵;Ulocal为局部物质点位移组成的矩阵;T为

式中:Xlocal为物质点坐标组成的矩阵 。
当得到变形梯度张量F后,便可以求得R和S。在大变形理论中,S与右柯西-格林张量Q的关系为
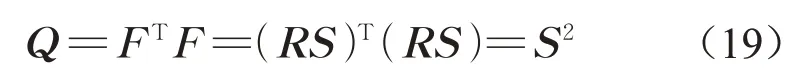
对于二维模型,当得到S的特征值λ1和λ2后,可以定义

使用矩阵特征值的特性,λ21和λ22为矩阵S2的特征值。

由于S为正定对称矩阵,所以λ1>0,λ2>0。

1.3 键断裂准则
为了描述材料损伤,标量函数μ(u,ξ)被引入了力密度-位移函数关系f(u,ξ)=μ(u,ξ)C·η。

式中:ℓc和γc分别为键伸长及键剪切的临界值。将能量释放率G分解为径向部分以及切向部分,有

式中:θ为键与球坐标系z轴的夹角;ϕ为键在Oxy平面的投影与x轴的夹角。可得

式中:Gc和Gs分别为Ι型能量释放率和ΙΙ型能量释放率。物质点x处的损伤值d(x)可按式(28)衡量:
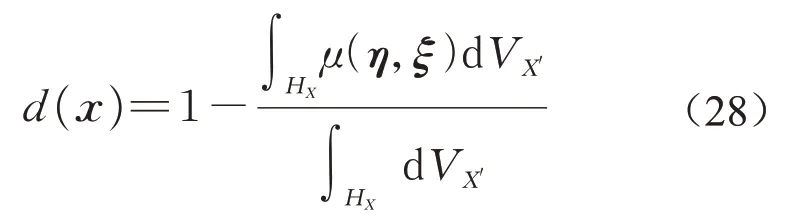
2 数值求解系统
利用动态松弛法模拟结构的准静态力学行为。对于整个系统,引入自适应阻尼系数cn结合虚拟对角质量矩阵M[38],建立加速度向量Ü、速度向量U̇和力向量F之间的关系,如式(1):

利用中心差分显式积分,相邻迭代步间的位移关系可以写成

其中初始迭代步的速度向量为

随后迭代步的速度向量通过式(32)计算:

对角质量矩阵M中的主对角元素必须满足

式中:Kij可采用文献[22]方法组成的刚度矩阵。每一迭代步的自适应阻尼系数取决于

式中:L为对角局部刚度矩阵,通过式(35)计算:
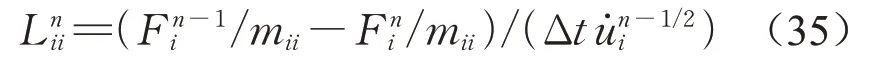
需注意,如果遇到速度为零的情况,Lii便设为零。
3 算例验证
进行相关基准测试以验证所提出的XPD模型在大变形分析中的可靠性。3.1节分析承受集中荷载的悬臂梁,这是一个经典的基准问题。3.2节引入了一个L形板来测试XPD大变形预测的有效性。最后将大变形XPD结果与大变形有限元结果进行对比,以验证所建立模型的准确性。假设模型为平面应力情况,单位厚度。
3.1 承受集中力的悬臂梁
悬臂梁的几何形状、边界条件和加载条件如图3所示。其中,杨氏模量为1 000MPa,泊松比为零。对于XPD离散,近场域δ=0.175m,网格间距Δx=0.05m(与有限元分析的网格尺寸相同)。为了在左边缘施加边界条件,将物质点的虚拟层添加到离散化模型中(见图4左端面外侧物质点,宽度为δ,高度为1m),并且这些虚拟点的所有自由度都设置为零。

图3 悬臂梁的几何尺寸与边界条件(单位:m)Fig.3 Cantilever beam:geometry and boundary conditions(unit:m)

图4 物质点分布与变形示意Fig.4 Material point distribution and its deformation
图5、图6展示了线性XPD、非线性XPD和非线性FEM预测的位移分布。通过对比可以看出,图5结果与图6结果有显著差异,因为在小变形理论中,位移随着外力的增加呈线性增长,即计算仅依赖模型的初始位置,而在大变形理论中,每对物质点之间的相互作用力由模型刚体位移转动后的变形确定。由图6可知,大变形XPD预测与大变形有限元预测结果吻合较好,2个方向的位移分量都显示出非常好的一致性。图7呈现了整个加载过程中记录的挠度荷载信息,表明大变形XPD方法与大变形有限元方法的加载路径几乎相同。

图5 使用小变形理论预测的x2方向位移云图Fig.5 Contour maps predicted by using small deformation theory

图6 使用大变形理论预测的x2方向位移云图Fig.6 Contour maps predicted by using large deformation theory

图7 悬臂梁的挠度-荷载分析Fig.7 Cantilever beam:deflection-load analysis
3.2 承受竖向面力的L型板
考虑几何非线性和材料损伤行为的共同影响。L形板在其右上侧面承受竖直载荷,几何尺寸和边界条件如图8所示。杨氏模量设置为1 000MPa、泊松比设置为ν=0.1。对于XPD离散化,δ=0.35m且Δx=0.1m。

图8 L形板的几何尺寸与边界条件(单位:m)Fig.8 L-shaped plate:geometry and boundary conditions(unit:m)
记录F=70 000kN时的位移分量的云图,图9和图10的结果表明,这2种方法在求解结果上产生的差异很小。

图9 L形板的使用大变形理论预测的x2方向位移云图Fig.9 L-shaped plate:displacement distribution predicted by using large deformation theory

图10 L形板的上表面位移Fig.10 L-shaped plate:x2-direction displacement on upper surface
图11描绘了L形板上表面在2个不同加载阶段的x2方向的位移。图12记录了板上表面3个不同点的位移-荷载曲线。从这些比较中可以看出,大变形XPD预测与大变形FEM的解几乎一致。

图11 L形板上3个指定点的位移-荷载曲线Fig.11 L-shaped plate:x2-direction displacementload curves of three specified points
图12是大变形XPD的断裂模拟。将临界能量释放率设为456 J·mm-2时,损伤在F=74 000kN处开始演化。如果检测到任何键断裂,加载将不会继续,而是等待系统迭代收敛再检测断裂,直至没有断裂发生才会继续加载。在大约F=131 000kN时,载荷不会增加,而L形板将继续向左侧尖端撕裂。图12中呈现的变形模式与文献[39]中的结果非常吻合。

图12 L形板的大变形XPD预测的损伤模式Fig.12 L-shaped plate:damage patterns predicted by large deformation XPD
4 结语
基于扩展键基近场动力学模型提出了一种数值实现方法。通过应用变形梯度张量在新的求解框架中很好地解决了几何非线性问题。在几组基准测试研究中,通过新框架模拟结果与大变形有限元结果之间的对比验证了模型的有效性和准确性。同时,该模型还能很好地模拟伴随大变形的材料非线性行为,包括裂纹扩展等。与小变形模型相比,除了每一步需要更新粒子的位置外,并没有增加额外的计算消耗。鉴于其预测变形的能力以及编码简单的优势,扩展键基近场动力学模型有望成为解决工程实践中复杂问题的有效工具。
作者贡献声明:
朱其志:提供研究平台以及理论基础,进行研究指导以及写作指导。
李惟简:进行方法创新以及程序实现。
尤 涛:提供编程帮助。
曹亚军:提供理论及创新思路。
