双向二维快速伺服刀架的前馈控制研究
2022-05-13武志士李国平邓益民赵琪啸徐少岩杨依领宁波大学机械工程与力学学院浙江宁波315211
武志士,李国平,邓益民,赵琪啸,徐少岩,杨依领(宁波大学 机械工程与力学学院, 浙江 宁波 315211)
0 引言
快速伺服刀架是指伺服控制的快速进给刀架系统[1],主要用于精密制造。配合快速伺服刀架,可使刀具产生快速而微小行程的高精度进给运动(位置精度可达纳米级)。此外,快速伺服刀架还可实时跟踪设计表面形状,能在一次加工中获得高精度表面轮廓及可用于复杂表面形状的精密加工[2]。基于这些优点,快速伺服刀架技术已成为一种重要的微结构表面加工方法。快刀伺服系统具有的快速性要求其驱动器能产生高频运动,压电陶瓷致动器可以满足这一要求。因此,许多学者提出并实现了由压电陶瓷致动器驱动快速伺服刀架系统。通过引入柔性铰链作为位移放大机构,快速刀架能实现大位移输出[3]。引入放大机构使刀架位移输出有较大的增长[4],但同时导致了响应频率降低[5]。压电陶瓷致动器的另一个特点是正向运动的性能比反向运动的性能好,反向运动时间较长使整体运动时间长。通过对向放置压电陶瓷致动器能有效地消除反向运动的负面影响,从而减少快速伺服刀架的响应时间。当一个制动器前进同时另一个制动器后退,反向力夹持下比单个制动器驱动时响应快。因此,双向驱动的快速伺服刀架比单向驱动的快速伺服刀架频率响应快[6-7]。由于一些复杂轮廓的加工需较复杂的伺服运动,而单自由度快速伺服刀架无法实现。因此,多自由度快速伺服刀架[8-9]已倍受关注。
压电陶瓷制动器存在迟滞特性,将降低快速伺服刀架的输出定位精度。为了消除迟滞的影响,需要通过构建迟滞模型建立前馈控制。已有研究中,建模方法主要有Preisach模型[10]、Prandtle- Ishlinskii模型[11]及Maxwell模型等[12- 14],但由于数学理论发展的局限性,这些模型的准确率已达极限。近年来引入了其他一些滞后模型(如Bouc-Wen模型[15-16]、LuGre模型[17]等),并取得了较好的效果。与其他迟滞模型相比,Bouc-Wen模型具有计算简单,易得到逆模型,待求参数少的优点,但其存在参数冗余问题,导致经典Bouc-Wen模型的参数难以识别,阻碍了其应用。通过归一化处理能保证Bouc-Wen只依赖于一组特定的参数。
本文搭建了基于双向压电驱动的二自由度快速伺服刀架的实验测试平台,获得了具有迟滞特性的位移曲线。然后采用基因遗传算法求解了Bouc- Wen模型的参数,对其进行求逆运算解得逆模型。最后依据逆模型构建了前馈控制环节,对快速伺服刀架进行了不同电压信号下的运动补偿及二自由度运动性能测试。
1 Bouc-Wen模型及其归一化
1.1 经典Bouc-Wen模型回顾
Preasch、PI、Bouc-Wen和Duhen模型等都对迟滞特性有准确描述。经典Bouc-Wen模型是由Bouc提出,被Wen进一步修改以模拟振动力学的滞后现象。Bouc-Wen模型具有能描述多种迟滞类别的能力和易计算的优点,这使大多数研究人员致力于探索该新兴模型的广泛使用。该模型输入和输出间的关系为
y(V,t)=αkV(t)+(1-α)Dkh(t)
(1)
(2)
式中:y(V,t)为滞后输出位移;V(t)为输入到快刀伺服刀架的电压;αkV是模型中弹性项和由参数α、k、D组成的纯滞后项(1-α)Dkh;h(t)为迟滞效应的辅助变量,它是非线性一阶微分方程(2)关于参数A、β、γ、n(n≥1)的解。通过正确选取这些参数值,可获得范围广泛的迟滞曲线。
1.2 归一化处理
迄今为止,许多研究工作都聚焦在Bouc-Wen模型的不对称性上,而经典Bouc-Wen模型中存在的参数冗余问题同样制约着模型的应用。因此,有必要对Bouc-Wen模型进行归一化处理,以避免参数冗余问题。为了准确描述普遍的参数冗余问题,现给出两组不同参数:n1=n2=n,A1=A2,α1=α2,k1=k2,β2=cnβ1,γ2=cnγ1,D2=cD1,其中c为正常数,初始条件h1(0)=h2(0)=0。因此,式(1)、(2)中Bouc-Wen模型可改写为以下两种形式:
(3)
及:
(4)
根据给定参数,方程(4)可转化为
(5)
令ha(t)=ch2(t),则方程(5)可表示为
(6)

y(V,t)=kvV(t)+khћ(t)
(7)
(8)
图1为归一化Bouc-Wen模型在一组特定参数下得到的迟滞曲线。

图1 模型生成迟滞曲线
1.3 模型求逆
除了避免参数冗余问题外,归一化后Bouc-Wen还具有逆模型易取的特点。根据式(7)、(8)可以求得归一化后Bouc-Wen模型输入、输出间的关系为
(9)
式中:yd(t)为预期位移;Vb为对输出电压施加的偏置电压,从而避免信号电压中出现负值;h(t)是由非线性微分方程求解得到,代表逆模型中的迟滞环节。kv、kh是模型中待求取的参数,由遗传算法得到。因此,通过简单的运算可得补偿后的输入电压。
2 实验测试平台搭建
为了对快速伺服刀架进行任意信号的输入控制及输出测量,搭建了实验平台。其中4个压电陶瓷驱动器(直径∅7 mm,长28 mm,自由行程30 μm)用于产生高精度输入位移。使用两个光学位移传感器(Keyence,LK-G80,分辨率为0.15 μm)测量末端执行器的响应。电压放大器的电压调节范围为0~150 V。使用的A/D模块型号为NI-PCI-6221。整个测试系统基于Labview软件实现。
3 参数识别
归一化Bouc-Wen模型中仅含有kv、kh、ρ、σ和n5个未知参数,因而求解工作减少。最小均方根算法、粒子群优化算法和差分进化算法等智能算法常被用以求取Bouc-Wen模型参数。本文使用了在稳定性和收敛速度上均优于传统遗传算法的自适应遗传算法,其流程图如图2所示。

图2 参数求解流程图
本文选择均方根误差来评判模型与真实值之间的偏差:
(10)
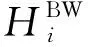
验证实验中所使用的输入为正弦波电压信号及由实验所测得快速伺服刀架的位移。虽然在自适应遗传算法中设置更多的种群数和遗传代数会提高拟合精度,但增加了时间。因此,本文选择初始种群为50,遗传代数为100,求解后结果如表1所示。

表1 Bouc-Wen模型参数表
由表1可看出,正弦波最佳适应度为0.28 μm,这说明归一化Bouc-Wen模型预测的结果与实验拟合度较高。
将求得参数代入归一化后Bouc-Wen模型中,可获得预测的位移曲线如图3所示。图中,实验曲线是通过施加一个正弦波电压信号(振幅75 V,频率1 Hz)到快速伺服刀架测得。

图3 模型预测曲线(正弦波)图
由图3可看出,模型值与实验值产生的误差主要位于峰顶处。由图3中误差曲线可知,在初始加载过程中实验与模型出现最大误差,每个峰值的偏差比其他时间大。这是因为归一化Bouc-Wen模型存在非线性微分方程,其求解结果为近似值,具有一定偏差,且在每个峰顶处,电压信号的变化率最大。这些因素一起作用导致了归一化Bouc-Wen预测曲线在每个峰顶偏差较大。初始部分出现最大偏差的原因是实验获取的位移曲线在开始阶段表现出较强的非线性,这使模型无法准确预测。
4 补偿与验证
图4为对快速伺服刀架进行迟滞补偿的结构图。图中,yd(t) 为期望得到的位移,u(t) 为Bouc-Wen逆模型产生的驱动电压,y(t) 为得到的驱动电压u(t)施加到快速伺服刀架后得到的实际位移,FTS为快速伺服刀架。以期望位移作为输入,输出为补偿电压,将得到的具有补偿效果的电压信号施加到快速伺服刀架,可得补偿后的实验位移。通过实验可知,前馈控制下快速伺服刀架能准确地得到期望轨迹。
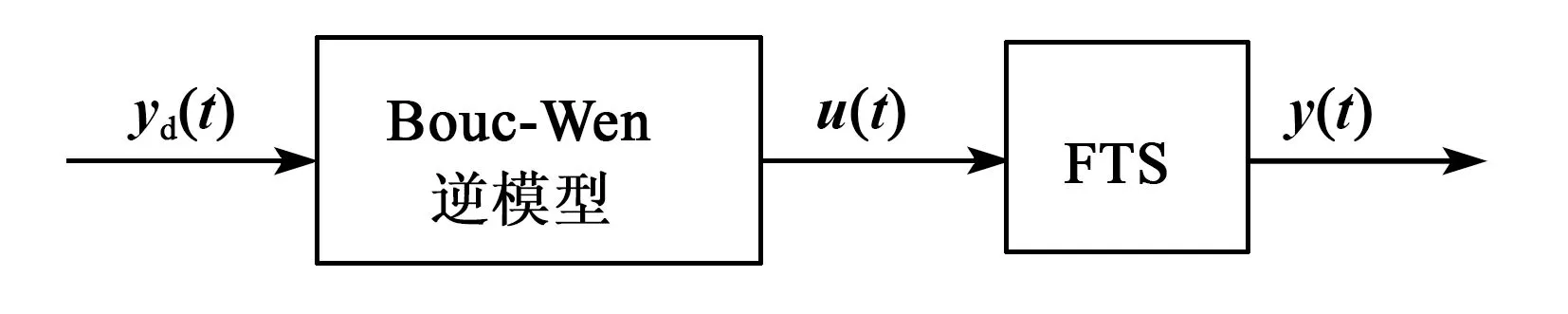
图4 前馈迟滞补偿流程图
为进一步验证模型的有效性,采用幅值45 μm、频率1 Hz的等幅正弦波期望位移信号进行轨迹跟踪实验。式(9)得到了补偿电压在每一时刻的数值。因为有偏置电压Vb的存在,所以理想电压与补偿电压的起点都不为0,如图5所示。由图可看出,在上升阶段,补偿电压大于理想电压;下降阶段,补偿电压小于理想电压。这种反差可补偿快刀伺服刀架中存在的迟滞特性。

图5 电压对比图
通过激光位移传感器测得消除迟滞后的位移,其与理想位移的对比如图6所示。由图可看出,前馈控制下快速伺服刀架的末端位移输出与期望位移吻合,最大轨迹跟踪误差发生在初始时刻。计算得到期望与实验的线性度为4.5%。由此可推断,基于Bouc-Wen模型的前馈控制能有效地消除快速伺服刀架的迟滞效应,从而提高快速伺服刀架的运动定位精度。
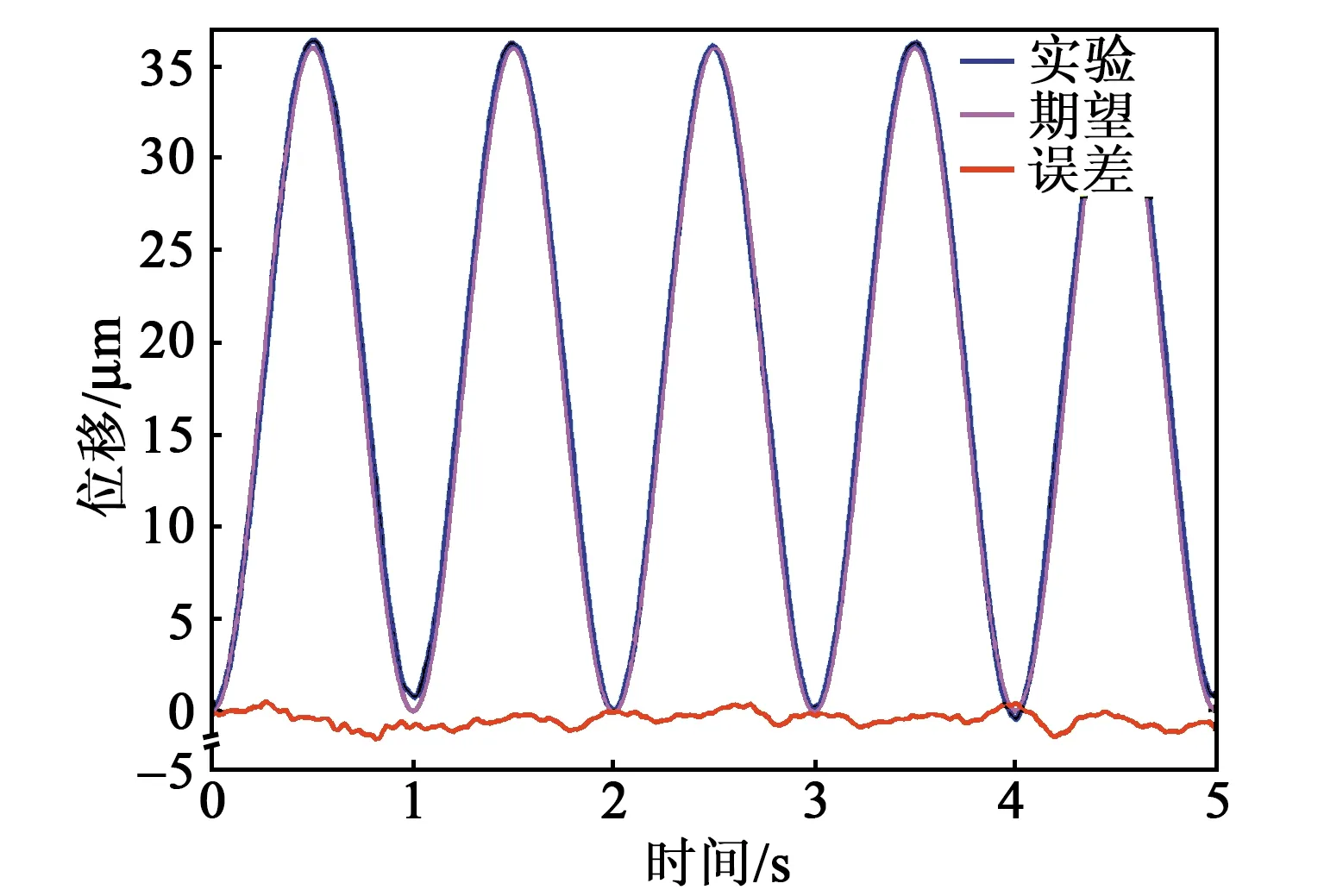
图6 实验位移曲线(正弦波)图
为进一步验证前馈补偿法,执行了快速伺服刀架在变幅正弦波位移轨迹下的运动性能测试实验。测得实验曲线与期望位移如图7所示。由图可看出,迟滞补偿下实验位移消除了迟滞特性的影响,与理想位移基本吻合。再次证明了基于Bouc-Wen模型迟滞建模的前馈补偿对快速伺服刀架中存在的迟滞特性消除的有效性

图7 实验位移曲线(变幅正弦波)图
表2为基于归一化Bouc-Wen模型的前馈补偿控制在不同期望跟踪位移下对快速伺服刀架定位精度的改善效果。由表可知,本文使用的基于归一化Bouc-Wen迟滞模型的补偿法能在很大程度上削弱由压电陶瓷驱动器所引起的迟滞误差,有效地提高了快速伺服刀架的驱动定位精度。为进一步提高快速伺服刀架的轨迹跟踪精度及模型的稳定性,有必要引入反馈控制。

表2 不同驱动信号的误差比较
5 二维性能测试
一些复杂曲面的加工要求快速伺服刀架能实现多维运动,因此,本文对提出的快速伺服刀架进行了两自由度运动性能测试。为了实现两自由度运动,两个压电陶瓷制动器分别安装在x、y方向上。对每个方向上预紧的压电陶瓷致动器施加特定电压信号,最终快速伺服刀架的末端位移输出曲线即是所选定的二维曲线。为了体现提出的快速伺服刀架二自由度运动性能,以圆轨迹为参考,选择余弦信号驱动x方向的压电陶瓷致动器A,正弦信号驱动y方向的压电陶瓷致动器B。两路激光位移传感器同时测得两个方向的快速伺服刀架末端的位移输出,将测得位移作图可获得快速伺服刀架输出的圆形轨迹。然而,由于压电陶瓷致动器中存在的迟滞特性,导致了测得的轨迹更偏向于椭圆。因此,为获取更精确的轨迹跟踪,有必要在二自由度运动中引入前馈控制。将期望位移分解成两个方向上的单向期望位移,并将其输入Bouc-Wen逆模型中,求得两个方向上的补偿电压。将求得的补偿电压作为输入,可获得了迟滞补偿后的位移曲线。图8为补偿前、后快速伺服刀架输出的二维曲线对比图。


图8 二自由度运动曲线图
由图8可看出,补偿后二维轨迹曲线更接近于圆。而补偿前曲线由于受迟滞特性的影响,在实验位移x=0,y=45 μm或x=45 μm,y=0部分与参考轨迹偏差较大。补偿前、后曲线在峰顶处偏差较大,一方面因受模型制约,另一方面因两个方向的预紧力不同。以实验与参考曲线对应点的欧式距离作为两者之间适应度d的表征值,能对快速伺服刀架的二自由度运动性能进行定量分析。适应度d为
(11)
式中:xi,yi分别为由激光位移传感器测得的x、y方向上的实验位移;xri,yri为对应的参考曲线上点的位移。
将实验数据代入式(11)可得到补偿曲线的最大拟合误差为4.486%,远小于未补偿曲线的最大拟合误差(14.683%)。表明提出的二自由度快速伺服刀架在前馈控制的补偿下具有较好的运动性能及优良的轨迹跟踪能力。而引起误差的原因,除控制模型本身存在的因素,两个方向上存在的制造误差也使输出位移与期望位移不同。
6 结束语
由压电陶瓷制动器驱动的快速伺服刀架具有频率高及输出力大等优点。但压电材料中存在的迟滞特性严重影响了其输出位移定位精度。简化后的Bouc-Wen模型具有参数少及易取逆的优点,利用自适应遗传算法可求得模型中的参数。实验结果表明,归一化后Bouc-Wen模型能很好地描述双向压电驱动的具有二自由度运动的快速伺服刀架中的迟滞现象。基于简化后Bouc-Wen模型搭建了前馈控制环节,并对快速伺服刀架进行了运动性能测试。结果表明,在前馈控制的补偿作用下,快速伺服刀架定位精度得到提高。同时,也证明了该快速伺服刀架具有优异的二自由度运动性能。
