基于有限元分层级联技术SAW滤波器精确计算

陈正林，赵雪梅，贺 艺，潘虹芝，白 涛，杜雪松，李桦林，肖 强，陈彦光，马晋毅(1.模拟集成电路重点实验室, 重庆400060；.中国电子科技集团公司 第二十六研究所, 重庆400060)

0 引言

声表面波(SAW)器件因具有低插损、高矩形度、小体积和低成本等优良特性而被广泛应用于雷达、通信和电子对抗等领域[1-3]。随着系统的快速发展，对SAW器件的损耗、带宽和频率温度系数等指标提出了越来越高的要求。因此，迫切需要发展能快速精准分析各种复杂边界条件下SAW器件的理论模型，并实现工程化应用和突破。

SAW器件精确理论计算过程复杂。2004年南京大学水永安教授和王为标[4]率先在国内实现了有限长结构SAW器件有限元/边界元法(FEM/BEM)精确计算方法，对于具有200根叉指电极的SAW谐振器每频率点计算时间约需5 min，且随着指条数的增加，计算时间也将增加，使得FEM/BEM难以满足高效率工程化应用[5]。K.Hashimoto等[6]提出了有限元/谱元法(FEM/SDA)方法，通过简化边界元计算实现了多层复合薄膜结构SAW器件的精确分析，然而对于近年来出现的多样化、复杂化新型多层薄膜结构SAW器件，FEM/SDA法无能为力[7]。与FEM/BEM和FEM/SDA法相比，FEM可分析具有任意多层薄膜结构、几何结构、边界条件及材料类型的SAW器件，并实现声学模式完整信息的获取[8]。但是FEM模型必须有足够细的网格和自由度，才能得到较精确的解。因此，FEM需要消耗大量的计算机资源[5]。

为了能够利用FEM可灵活处理任意结构、电极形貌及材料选型的优势，且兼顾计算效率和工程化应用，2016年，Koskela等[9]创新性地给出了二维有限元分层级联技术(HCT)模型，尽管计算效率有较大改进，但仍存在因各种理想假设导致的精度不足问题。近年来，K. Hashimoto等[10]和Koskela等[11]在分层级联技术基础上结合图形加速器(GPGPU)加速技术，对各类型的SAW器件进行了计算，由于该模型未充分考虑SAW器件实际工艺因素，从而限制了该方法的工程化应用。

本文基于分层级联算法推导用于描述有限长结构SAW器件的有限元数学模型。该有限元数学模型充分考虑了压电材料的传播损耗、介电损耗、电极粘滞损耗及电阻损耗等因素，结合GPGPU加速技术，提高了有限长SAW器件的计算速度，缩减了完整SAW器件的计算时间。基于全波仿真技术，考虑了管座及键合线等封装模型电磁效应，对漏波型42°Y-XLiTaO3温度补偿型声表面波(TC-SAW)器件进行计算并研制了样品，计算所得结果与实验结果吻合较好。

1 分层级联基础理论

HCT是以FEM为基础，结合有限元自由度降阶技术，从而实现快速计算。因此，分层级联技术既保留了FEM可任意处理多层薄膜结构、几何结构、边界条件及材料类型的优势，又克服了FEM自由度庞大的缺点。

1.1 分层级联理论

图1(a)为TC-SAW器件的分层级联单元结构示意图。压电材料上覆盖一层SiO2作为温度补偿层，底部完美匹配层(PML)用于吸收反射波，级联单元结合实际工艺情况，并考虑电极的倾斜形貌。图1(b)为相应的分层级联单元有限元网格示意图。其中，XL，XR分别为单指结构有限元模型的左、右边界自由度。

由于有限长SAW器件结构由具有周期性或非周期性的单指单元构成，根据级联单元左右边界力学量和电学量的连续性原理，将2个或2个以上的单指单元联成完整SAW结构(见图2)，每次级联都是以2n的形式增加，级联9次可完成512根指条的计算。

压电体是各向异性的电介质，在外力作用下发生形变时，物质结构变化引起介质电极化，称为压电效应。压电效应反映了力学量和电学量间的相互耦合作用。除弹性应变场和应力场外，同时还存在电场和电位移场，且其相互作用。本文仍将讨论局限于线性范围，可任意取1个力学量和1个电学量作为自变量。因此，本文将应变和电场强度作为自变量，根据胡克定律和电学关系可得到应力和电位移的本构方程。应力及电位移[3]以张量的形式可表示为

(1)

(2)

根据胡克定律，应变S和位移u间的关系以张量的形式表示为

(3)

其中：

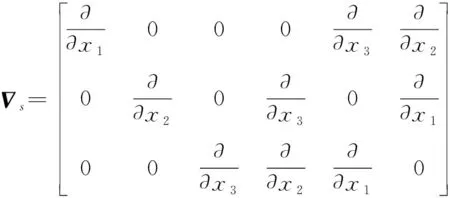
(4)

根据电学可知，电场强度E和电势φ之间的关系为

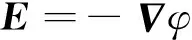
(5)

根据牛顿第二定律和麦克斯韦方程，得到SAW器件的压电平衡方程以张量形式表示为

(6)

(7)

式中ρ为电荷密度。采用FEM求解式(6)、(7)可得表征分层级联单元(见图2)的系统矩阵:

(8)

式中:K为刚度矩阵;M为质量矩阵;XL，XI，XR分别为单指结构有限元模型的左边界、内部、右边界自由度(分别包括位移和电势自由度)；RA，RI，RB为左边界、内部及右边界外力；v为电极表面电势自由度；q为电极表面电荷量;ω为角频率。

在无外力作用时，则RA=0，RI=0，RB=0，对式(8)进行整理可得：

(9)

其中，A=K-ω2M。

采用有限元降阶技术和自由度压缩法，将内部自由度XI消除，XI为

(10)

对式(9)消除XI，可将系统矩阵由4×4矩阵降维为3×3矩阵，即：

(11)

对式(11)进行整理可得表征SAW结构单指单元的B矩阵，即：

(12)

式(12)只包含XL、XR、v自由度，等价于分层级联单元的系统矩阵方程(9)，但系统矩阵方程(12)所包含的自由度远小于系统矩阵方程(9)，减少了需要计算的自由度。式(12)结合图1(b)中单指结构左右边界声学量和电学量连续性条件，得到级联单元A和级联单元B的级联系统矩阵方程：

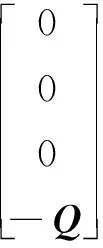
(13)

式中：X′L为级联单元A的左边界；X′I为级联单元A、B的相邻边界；X′R为级联单元B的右边界自由度；V=[VA,VB]，Q=[qA,qB]分别为级联单元A、B级联后的电压自由度。由式(13)可看出，分层级联的本质和P矩阵级联相同，即将声学参量串联、电学端并联。

通过式(13)重复采用式(9)～(12)进行自由度消除和级联，得到包含整个器件的电压自由度和电荷量，并能表征完整有限长结构的矩阵方程：

(14)

求解式(14)需考虑传播方向上的左右二端PML吸收层，同时根据整个器件电荷量为0，求取有限长SAW滤波器结构的Vref。

1.2 全波仿真理论

从SAW器件单指结构式(9)到能够表征有限长SAW器件的系统矩阵方程(14)，分层级联算法采用有限元降阶技术和GPGPU加速技术相结合，求解式(14)可得有限长SAW器件的声/电响应特性。

对于更高频率和更小尺寸的器件，封装结构对SAW器件的电学性能影响明显。图3为基于全波仿真分析准确地模拟SAW器件特性的模型。设计过程中，考虑了整个封装的电磁效应，该模型包括SAW滤波器电路拓扑结构及在HFSS软件中构建的射频滤波器封装结构。

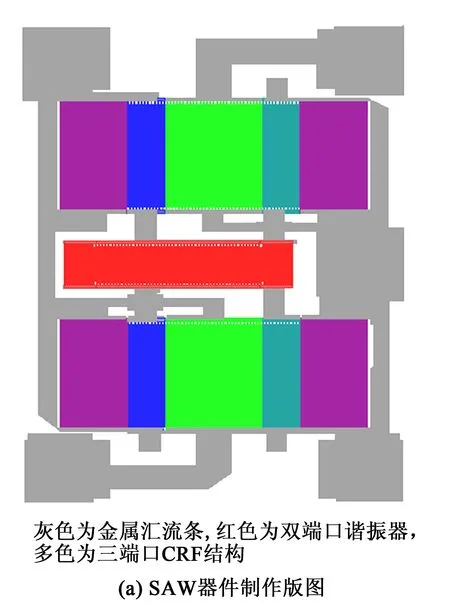
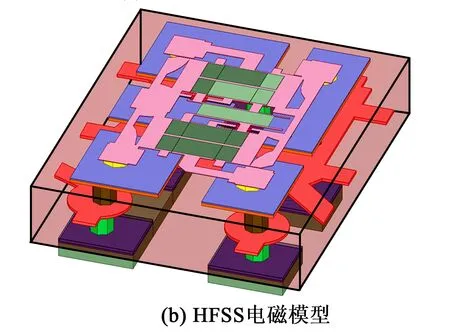
图3 全波仿真模型

根据图3(a)的电路拓扑结构研制了相应的SAW滤波器，其中以42°Y-XLiTaO3作为衬底，Al电极厚为210 nm，SiO2厚为1 430 nm，滤波器中心频率设计为804.14 MHz，相对带宽为3.1%，频率温度系数为-8.5×10-6/℃。图4为SAW滤波器的计算结果与实测的插损曲线。由图可知，仿真曲线与测量结果吻合良好，通带内的微小差异主要是由于有限元模型的声传播损耗设置所致。

图4 42°Y-XLiTaO3 TC-SAW滤波器计算结果和实测结果对比

2 结束语

基于有限元数学模型引入分层级联算法，从数学论证和物理意义上严格推导了有限长结构SAW器件的有限元数学模型。该模型充分考虑压电材料的传播损耗、介电损耗、电极粘滞损耗、电阻损耗及基于实际工艺条件下的电极形貌，使SAW器件的有限元模型尽可能地接近实际，得到用于表征有限长结构SAW器件的系统矩阵。引入有限元降阶技术和自由度压缩法，实现了有限长结构的系统矩阵降维和降阶。基于全波仿真分析，并结合有限元降阶技术和GPGPU加速技术，对42°Y-XLiTaO3TC-SAW滤波器进行了精准快速计算，经实验验证了该方法的准确性。