开口圆柱壳结构挠曲电传感特性分析

张旭方,刘 丽,王鹏飞,傅佳宏(浙大城市学院 工程学院机械电子工程学系，浙江 杭州 310015)

0 引言

为了分析工程中常见的开口圆柱壳结构振动特性，需要各种振动传感器。基于压电材料的压电传感器是常见的振动传感器，其利用压电材料的力-电耦合特性，设计传感器并进行传感特性分析[1-6]。但压电材料需预极化，使用时间过长，存在退极化现象。此外，压电材料(如PZT陶瓷等)通常含有铅元素，制备过程中会污染环境。因此，挠曲电材料作为一种新兴的力电耦合智能材料而备受关注。

正挠曲电效应反映了应变梯度与电场间的力-电耦合关系。近年来研究者基于挠曲电材料进行了大量的理论与实验研究，通过不同的理论与实验方法确定各种挠曲电材料的正、逆挠曲电系数的大小[7-8]。研究挠曲电材料的挠曲电系数是为了更好地掌握材料特性，为进一步设计各种挠曲电器件以应用于不同的工程中提供了良好的基础。

WANG等[9]论述了固体中的挠曲电效应近年来的发展、挑战与前景，给出了宏观与微观挠曲电效应的理论发展时间轴和里程碑成就。由于挠曲电效应是与梯度有关的效应，挠曲电效应在纳米微小尺度有广泛的应用[10-12]。近年来，基于宏观材料尺度的挠曲电效应引起了人们的关注。基于正挠曲电效应设计出各种挠曲电传感器、俘能器等，并对智能结构进行传感监测与能量采集研究[13-14]。HU等[15]已设计了基于一般双曲率壳结构的挠曲电传感器，根据不同结构的拉梅常数与曲率半径可将该传感器模型应用于不同的板壳结构。

基于正挠曲电效应，本文将建立基于开口圆柱壳结构的挠曲电传感器模型。首先分析开口圆柱壳在外部激励作用下的动态响应特性。根据正挠曲电效应建立挠曲电传感理论，并推导出外部负载两端的输出模态电压的表达式。当挠曲电片无限小时，基于挠电片的挠曲电传感理论简化为点的分布式传感特性。最后分析了不同参数对挠曲电传感信号的影响，对比不同方向弯曲应变引起的挠曲电信号的不同作用。

1 开口圆柱壳挠曲电传感器模型

1.1 挠曲电传感器模型

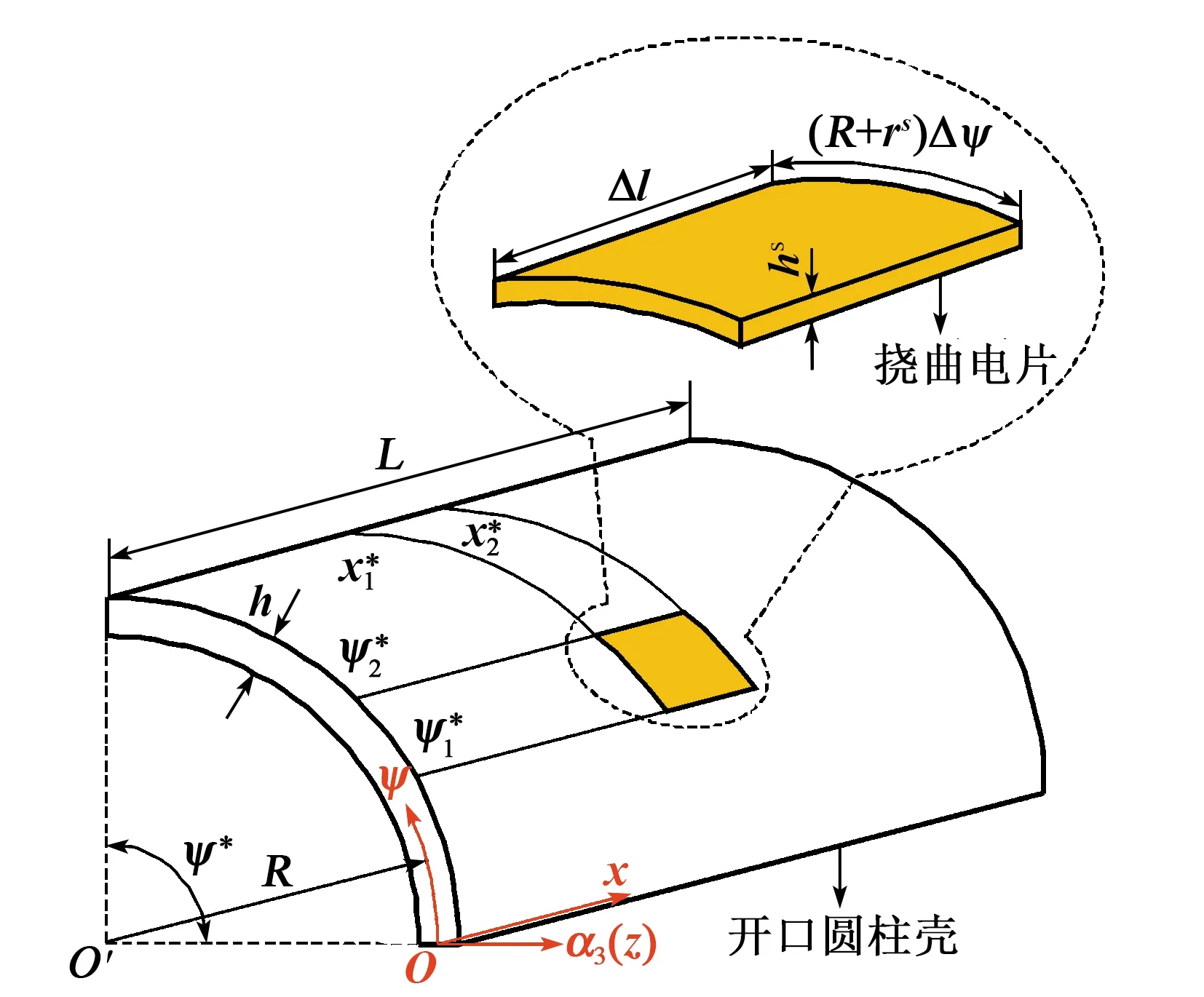
图1 开口圆柱壳挠曲电传感器模型

假设挠曲电片理想粘贴于开口圆柱壳的外表面上，根据Kirchhoff-Love薄壳理论，开口圆柱壳的应变[16]为

(1)

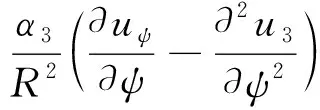
(2)

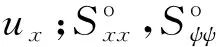
挠曲电效应主要与壳结构的应变梯度，即弯曲应变有关，弯曲应变为

(3)

(4)

1.2 挠曲电传感器动态响应

根据模态扩展法，动态位移响应uψ、u3可用模态参与因子ηmn(t)和模态函数Uimn(x,ψ)(i=x,ψ)[17]表示为

(5)

(6)

式中：∑∑表示所有参与模态的叠加；m,n分别为长度、周向方向(x、ψ方向)的模态数；Uψmn(x,ψ),U3mn(x,ψ) (下文简写为Uψmn，U3mn)分别为周向与横向振动的(m,n)阶模态函数。

结构的模态函数取决于结构的边界条件与结构尺寸。当开口圆柱壳四边简支时，结构的周向与横向振动模态函数[17-18]可表示为

(7)

(8)

式中B,C分别为模态函数的幅值。

ηmn(t)揭示了每阶模态振动响应在总的振动响应中所占比，模态参与因子的大小与每阶模态力的大小相关。当结构边界条件与尺寸确定后，模态阵型决定了传感信号的分布特性，模态参与因子决定了传感信号的大小幅值。

2 挠曲电传感信号分析

基于正挠曲电效应，不同方向的应变梯度在法向的梯度引起了法向的电位移。根据一般双曲率壳结构的挠曲电传感公式[15]，代入开口圆柱壳的曲率半径R与拉梅常数可得:

μ12(kxx+kψψ)+ε33E3

(9)

式中：μ12为挠曲电系数；ε33为介电常数；E3为法向电场强度。

通过将电位移在有效的传感面积Se上积分，求出开路状态下的信号电压[15]为

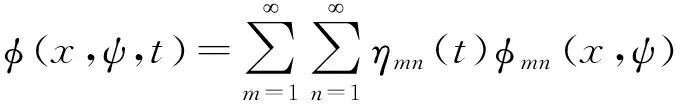
(10)

式中t为时间。

考虑每阶模态在共振状态下的传感信号，则(m,n)阶模态的模态电压[15]可表示为

(φmn)xx+(φmn)ψψ

(11)

对于挠曲电传感信号，模态电压信号φmn可分成(φmn)xx与(φmn)ψψ，分别表示为

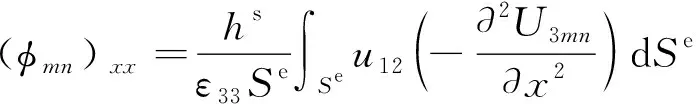
(12)

(13)

(14)

(15)

(16)

式中Lψ=Rψ*为开口圆柱壳圆周方向的长度。

根据式(14)～(16)可知，不同点对应的传感信号表示开口圆柱壳不同位置的传感信号。

3 变曲率开口圆柱壳分析

当L和Lψ保持不变时，ψ*对挠曲电传感特性有影响。Rψ*=Lψ保持不变时，此时ψ*与R成反比。y*=150°、120°、90°、60°、 30°时，R为Lψ/ψ*(见图2)。

当L和边界条件固定时，不同的ψ*对应的结构频率不同。每阶模态的固有频率分别为

(17)

(18)

(19)

(20)

(21)

(22)

(23)

a2=[1/(ρh)2](k11k33+k22k33+k11k22-

(24)

2k12k23k13-k11k22k33)

(25)

(26)

(27)

f1mn=ω1mn/2π

(28)

式中：ρ为板质量密度；Y为板杨氏模量；μ为泊松比；K为弯曲刚度;kij(i=1～3,j=1～3)、ai(i=1～3)、α均为求解过程中的系数ω1mn、f1mn为结构横向振动的固有频率。

4 数值仿真与优化

本文开口圆柱壳采用聚丙烯材料，挠曲电片使用a-聚偏氟乙烯(PVDF)薄膜材料。开口圆柱壳结构及挠曲电片的尺寸、材料参数如表1所示。

4.1 频率分析

讨论开口圆柱壳的挠曲电传感特性需首先明确开口圆柱壳结构每阶模态的固有频率。结构的固有频率越大，在相同模态力作用下，结构的振动响应越小。根据结构尺寸与参数，不同模态及弯曲角度下固有频率分布如图3所示。

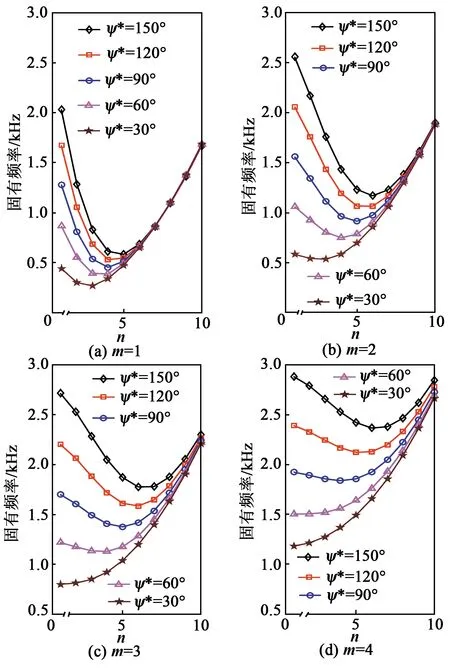
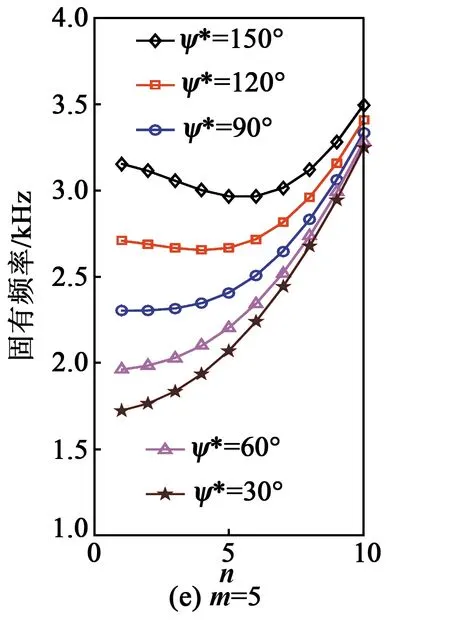
图3 不同模态下不同曲率的固有频率分析

由图3可看出：

1) 当m保持不变时，随着n增大，固有频率先减小再增大。ψ*越大，固有频率越大。即同样尺寸的开口圆柱壳结构周向越弯，固有频率越大，相同力作用下越难被激励，响应越小。

2) 当m增大时，n与ψ*下的固有频率增大，固有频率的变化趋势类似。m越大(如m=5)，ψ*越小。当开口圆柱壳周向越平(如ψ*=30°)时，固有频率随着n的增大而增大，即模态数越大，频率越大。

4.2 挠曲电传感特性分析

当ψ*=150°时，模态函数的幅值B、C分别为-1、1。模态分别为(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)时挠曲电传感特性如图4、5所示。

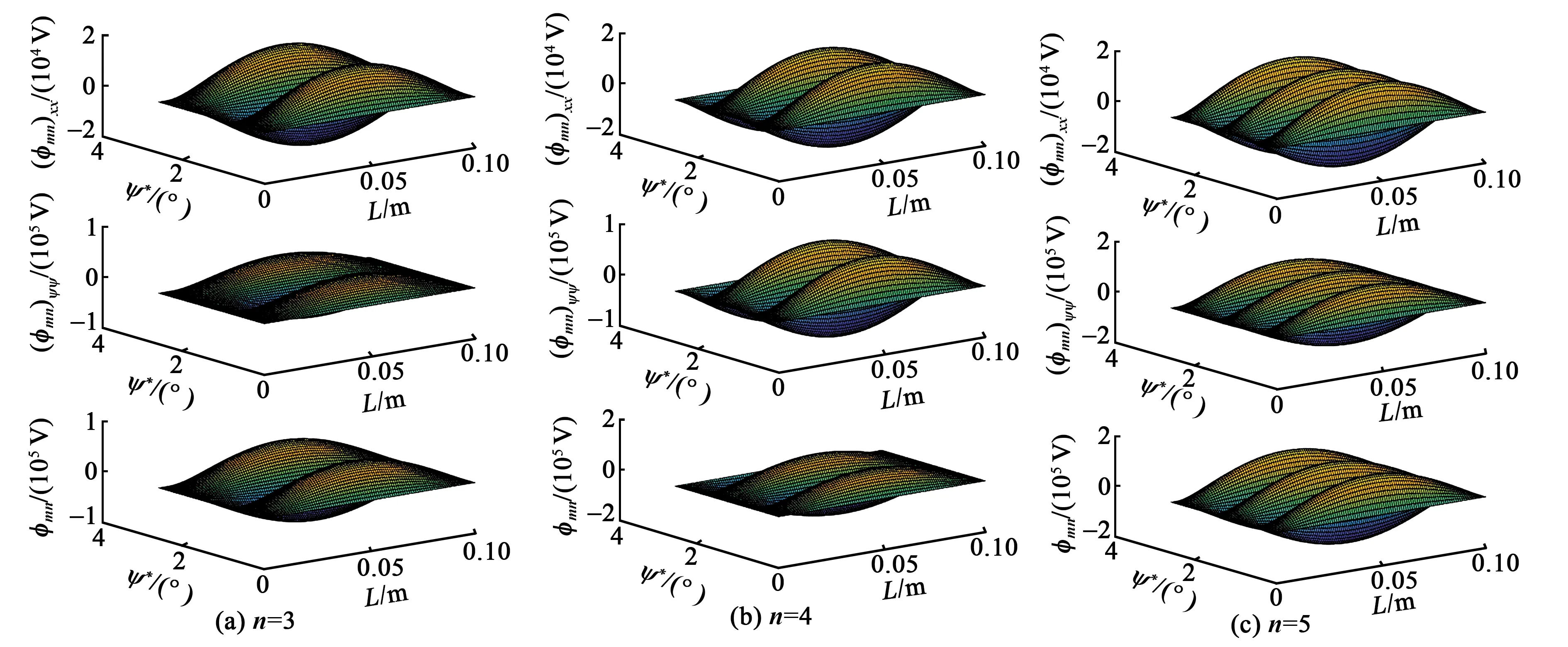
图4 m=1、n不同时挠曲电传感特性

图5 m=2、n不同时挠曲电传感特性

不同模态下挠曲电传感特性与模态的阵型有关。由图4可知，(φmn)xx较小， (φmn)ψψ占主导。对比图4、5可知，随着m的增大， (φmn)xx增强。

4.3 不同曲率对挠曲电传感特性影响

当L确定时，开口圆柱壳挠曲电传感器的传感特性与ψ*有关。不同模态下，分布式传感特性如图6所示。

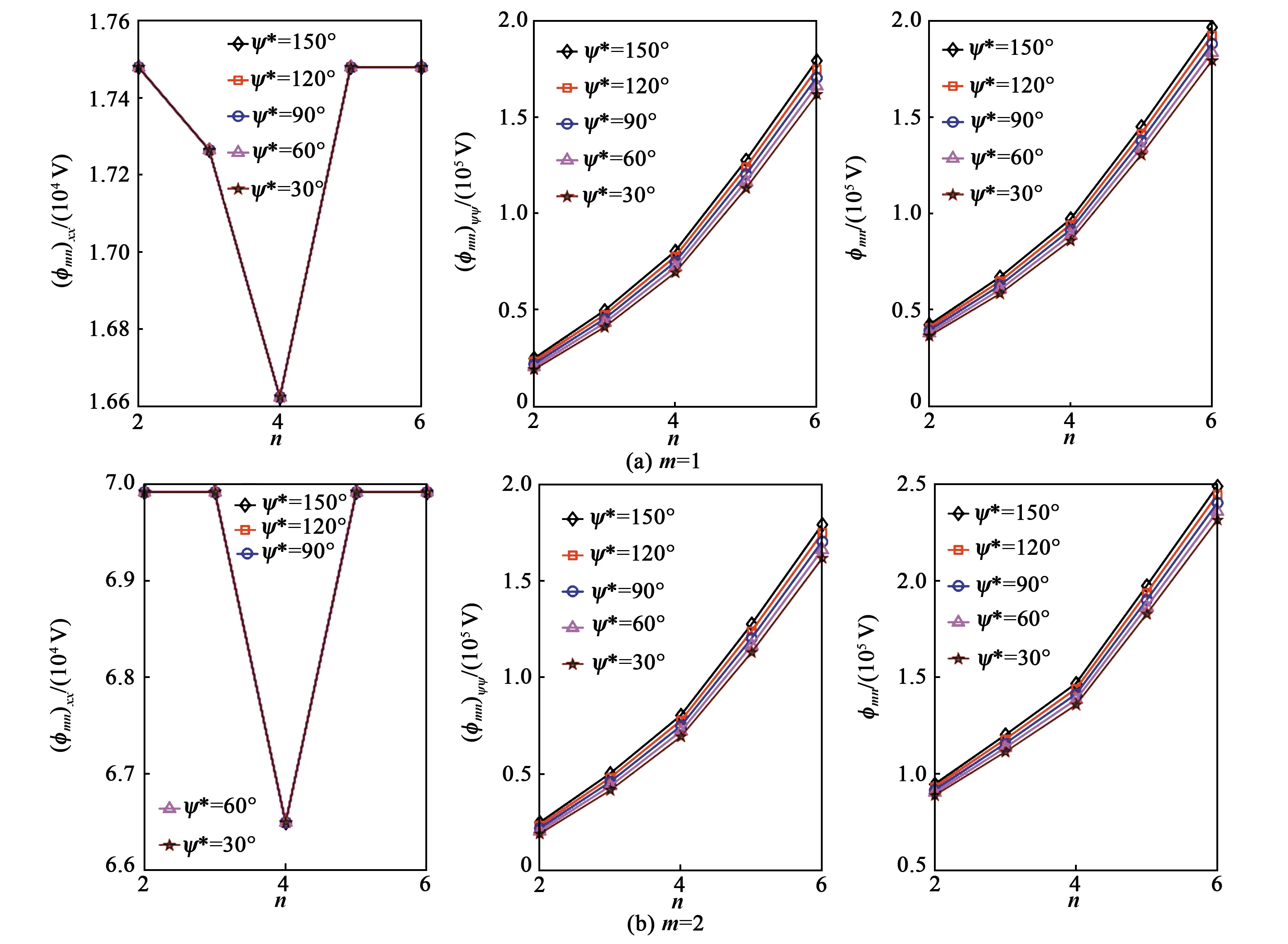
图6 不同ψ*的模态电压

当m=1或2且保持不变时， (φmn)xx不随ψ*的变化而变化。 (φmn)ψψ随着ψ*增大而增大，且随着n的增加而增大。弯曲角度与模态数越大，kψψ越大，则 (φmn)ψψ越大。

随着ψ*的增加，总弯曲应变引起的挠曲电传感信号增大；随着n增加，总弯曲应变引起的挠曲电传感信号增大。总弯曲应变作用中，kψψ占主导作用。

5 结论

本文基于正挠曲电效应建立了开口圆柱壳结构的挠曲电传感器模型，并分析了开口圆柱壳的挠曲电传感特性，讨论了不同的参数对传感特性的影响。根据分析结果可得如下结论：

1) 不同模态下固有频率不同，m不变时，随着n的增加，固有频率先减小再增加。

2) 随着周向方向弯曲角度的增大，固有频率增大。即周向越弯，固有频率越大，相同力越不易被激励。

3) 当m不变时，周向方向弯曲应变引起的挠曲电信号占主导，且挠曲电传感信号随着n的增加而变大。

4) 随着周向弯曲角度的增大，周向方向的弯曲应变引起的挠曲电信号增大，即周向方向越弯，圆周方向的应变梯度越大，引起的挠曲电传感信号越大。