低插损高频SAW滤波器的研究

王 巍,周杨春,王 方,谭纪伟,滕洪菠,李俊峰(重庆邮电大学 微电子工程重点实验室，重庆 400065)

0 引言

作为射频前端实现通信和导航等信号交互的关键芯片，声表面波(SAW)滤波器广泛应用于移动通信领域。梯形结构的SAW滤波器具有带宽、带外抑制设计灵活和低插损等特性，可适应不断升级的通信设备对SAW滤波器的性能要求，因而已作为设计高频低插损SAW滤波器时的首选结构[1-3]。为了获得更低插损，本文分析了SAW传播时能量分布随电极厚度的变化关系，采用0.33λ～0.36λ(λ为波长)的厚膜电极使声波能量限制于材料表面，降低了SAW传播时压电材料和模式转换对能量的消耗。

梯形SAW滤波器由串并联谐振器级联而成，谐振器性能直接影响器件的整体性能，其叉指电极在压电材料表面除激发和接收所需模式的SAW外，还有其他(如横向模的杂模)干扰[4-8]。横向模引入的尖峰损耗直接增大了滤波器的带内波动，且尖峰损耗出现的位置靠近中心频率，无法避免在通带内出现。研究发现，该干扰模主要由换能器、间隙和汇流条等不同结构区域的声速不同引起[9]。为了提高高频SAW滤波器的性能，减小带内横向模的干扰，本文研究了占空比、反射栅周期和叉指对数对通带的影响，并设计了一种叉指换能器(IDT)型反射栅结构，该结构对谐振器和一阶梯形滤波器的带内最大尖峰损耗在采取常用优化措施基础上进一步减小了0.55%和0.65%。

本文分析了“T”型和“π”型镜像拓扑结构与频率响应的关系，以4阶梯形结构为基础设计了“T+π”型镜像型拓扑结构，优化了器件的矩形度，并改善了普通梯形结构通带左右边缘的凹陷问题。基于COMSOL的有限元仿真结果表明，“T+π”型镜像型拓扑结构的中心频率为2.520 5 GHz，插入损耗为-0.502 12 dB，带内波动为0.646 89 dB,带宽大于98 MHz,带外抑制大于30 dB。

1 低插损特性的研究

如图1所示，SAW传播时，损耗主要来自边缘辐射、横向能量泄漏、材料的粘性损耗、电极的欧姆损耗及SAW向材料深度方向的能量泄漏和模式转换损耗[10]。瑞利波主要集中于材料表面，为了减小瑞利型SAW滤波器的插入损耗，应尽量使声能限制于材料表面，从而减小SAW传播时的能量泄漏。

1.1 模型的建立

瑞利波不存在声孔径方向上的位移[11],且孔径长度远大于电极宽度，因此，可采用平面假设[12]。基于COMSOL建立SAW器件的二维周期性结构如图2所示。底部设置为固定约束，左右两侧分别在固体力学和静电物理场中设置为周期性条件[13]，底部设置1个0.5λ(波长λ=1.6 μm)、材料为128°YX-LiNbO3的完美匹配层(PML)，以降低底面反射的影响[14]，电极材料为金属Al。

图2 二维周期性结构

1.2 结果分析

为了减小SAW在压电材料中传播时的损耗，应尽量使声能限制于LiNbO3材料的表面[15-16]。基于二维模型(见图2)将研究类型设置为“特征频率”，使用参数化扫描工具以0.05 μm为步长依次改变电极厚度，求解得到SAW传播时的能量密度分布随材料深度的变化关系如图3所示。图中，hAl为金属电极厚度，H为压电材料厚度。

图3 能量密度随渗入材料深度的变化

为了便于分析，已将图3的横坐标取反，小于0的部分对应二维形变图的0上部分(即金属电极的厚度)，大于0的部分对应二维形变图的0下部分(即压电材料的厚度)。由图3可看出，hAl<0.2 μm,即相对于电极周期膜厚小于12.5%时(图中虚线)，随着hAl的增加，在同一压电材料内部(同一横坐标位置)由压电效应引起的能量密度增加，说明更多的能量被传播到压电材料内部，不利于减小材料的粘性损耗、纵向能量泄漏及SAW向体波的转换损耗。在hAl为0.25～0.50 μm(相对厚度为15.6%～31.25%)内，随着hAl的增加，压电材料内的能量密度越来越小，则压电材料及通过压电材料转换消耗的能量降低。而总能量不变，通过能量守恒可推断出，趋于材料表面激发的瑞利型SAW的强度将得到提高。

每条叉指电极均为长方体形状的Al金属指条，以图1所示的方向看去，其横截面积S为

S=hAl×a

(1)

式中a为电极宽度。

每条电极的电阻为

(2)

式中：W为电极孔径；ρ为电阻率。

当ρ和a保持不变(本文均采用Al作为电极材料)时，R与hAl成反比。随着hAl的增加，电极的横截面积增大，电极电阻减小，则电极的欧姆损耗降低。

分析图3电极部分可得，随着电极厚度的增加，电极承受的功率逐渐上升，如果功率太高可能发生电极烧毁，这不利于器件的耐功率特性。设总体积为1，则单位面积下电极所承受的最大能量为

(3)

式中Pmax为不同电极承受的最大能量。

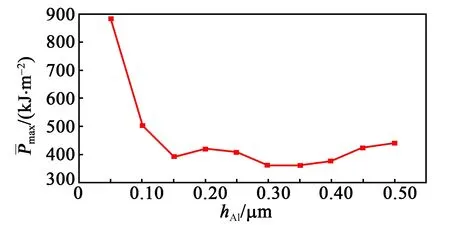
图4 单位电极面积承受的最大能量

2 减小横向模干扰

2.1 占空比的分析

占空比为

η=a/p

(4)

式中p=0.5λ为指间距。

对于均指结构，η=0.5。表1为器件结构参数。表中，N为叉指对数，Ng为反射栅对数。在COMSOL中分别建立串、并联谐振器及一阶梯形带通滤波器的二维等效模型[17]，并计算得到器件的频率响应，如图5所示。

表1 器件结构参数

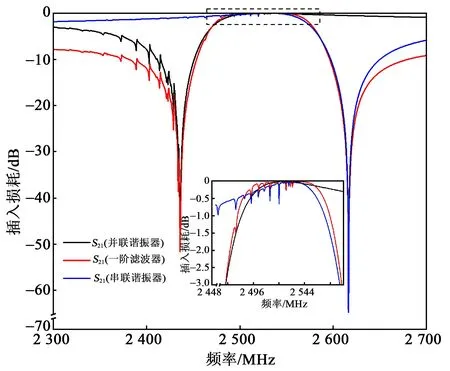
图5 器件的频率响应

由图5可知，采用厚膜电极(hAl=0.40 μm，即相对厚度>10%λ)的并联谐振器通带平滑，串联谐振器通带内出现横向模式干扰，并引入了尖峰损耗。而梯形SAW滤波器由串、并联谐振器相互级联，并通过电耦合实现，其通带内尖峰损耗出现的位置与串联谐振器中横向模式的谐振点位置一致。因此，对于梯形滤波器，其通带平坦度和纹波主要受串联谐振器影响。

图6为参数化扫描串联谐振器占空比η得到的一阶梯形SAW滤波器的频率响应。由图可得，带外抑制随着η的增大而减小，当η=20%时，滤波器的带外抑制最高，但通带出现凹陷，且插入损耗大，不适用低插入损耗指标的实现。η为40%～60%时，插入损耗降低至-1 dB内，但带宽随着η的增加而减小；当继续增加η=80%时，带宽反转增大，损耗降低，这有利于完成宽带低插入损耗的结构设计。为了提高梯形SAW滤波器的频率选择性，通常采取多级级联的方式，而η=40%的一阶滤波器的频率响应带内平均损耗较大，多级级联时通带损耗随着级联阶数的增加而增大，对实现低插入损耗指标不利。而η为50%、80%时，带宽基本相同，除尖峰损耗外，在η=80%时，带内整体损耗达最低，其频响特性适用于低插入损耗宽带滤波器的设计。但在2 515.5 MHz引入了一个尖峰损耗，使得滤波器的纹波和通带平坦度增大。由文献[10]可知，该损耗及其他幅值较小的尖峰损耗主要由换能器、间隙等区域的声速不同而造成的横向模式干扰。该模式因靠近中心频率而在通带内出现，但可采取级联不同叉指对数的串联谐振器、调整占空比和反射栅周期等措施削弱该模式的影响，使其降低到可接受范围内。

图6 不同η器件的频率响应

2.2 反射栅结构的分析

反射栅阵列的每根电极都会反射波，其中相位不同的波相互干扰并在一定波段内相互抵消，而相位相同的波相互叠加形成强烈的反射波[18]。因此，可采取调整反射栅结构的措施减小该干扰模式引入的损耗，并使其降低。

2.2.1 反射周期对横向模式的影响

图7 改变反射栅周期器件的频率响应

改变反射栅的周期大小，削弱反射栅阵列对尖峰损耗所对应的横向模式反射是针对横向模式干扰的常规优化措施。在hAl=0.4 μm的基础上，调整串联谐振器的η=80%，再次参数化扫描改变反射栅周期计算得到反射栅周期与一阶梯形滤波器频率响应的关系，如图7所示。由图可知，带内整体损耗和带宽变化较小。反射栅周期为0.6 μm时，最大尖峰损耗最小，通带最平坦，纹波最小。与图6相比，最大尖峰损耗由-1.254 45 dB降低至-0.708 85 dB，降低了43.49%，保障了η=80%时宽带宽、低插入损耗特性，同时使通带横向模式干扰引起的尖峰损耗降低到小于-1 dB，是可接受范围内。

2.2.2 IDT型反射栅

反射栅电极作为压电材料表面的金属电极阵列，在反射IDT激励的SAW时，由于压电效应，电极金属指条内将生成感应电荷。如果把这些电荷类似于接收IDT收集起来，则在反射栅汇流条中将产生频率为f0的感应电流。再通过逆压电效应，感应电流所产生的电场将反馈激励SAW，这将为SAW的传播提供能量补充，从而减小传播损耗。因此，为了进一步减小传播损耗和带内波动，本文设计了一种IDT型反射栅结构，如图8所示。每个反射栅周期内有一对叉指电极，类似于换能器的输入输出叉指电极，反射栅电极交错排列并分别接入4个不同的汇流条。

图8 采用IDT型反射栅的谐振器

对于谐振器的二维等效有限元模型，反射栅阵列不同的汇流条分别在静电物理场中设置为不同的悬浮电位端口，即每个谐振器的反射栅电极阵列1～4分别设置为4个不同的悬浮电位端口，对于由串、并联两个谐振器级联的一阶梯形滤波器，则需设置8个不同的悬浮电位端口。总之，设置反射栅边界条件的悬浮电位端口的数量为谐振器数量的4倍。

图9、10分别为采用IDT型反射栅和短路反射栅谐振器的频率响应对比图。由图可得，IDT型反射栅对未调整反射栅周期(λg=λ)的均指谐振器的带内最大尖峰损耗优化效率为8.84%，对采取占空比和反射栅周期优化措施后，谐振器的带内最大尖峰损耗进一步降低了0.55%。与采用短路反射栅的器件结构相比，采用IDT型反射栅的一阶梯形滤波器的传播损耗进一步降低，带内最大尖峰损耗降低了0.65%，如图11所示。这在选取厚膜电极和采取占空比和反射栅周期优化措施基础上，进一步减小了横向模式引入的尖峰损耗，提升了滤波器的通带性能。

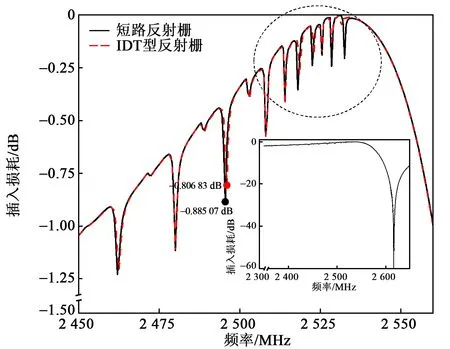
图9 IDT型反射栅对未采取均指谐振器的优化对比

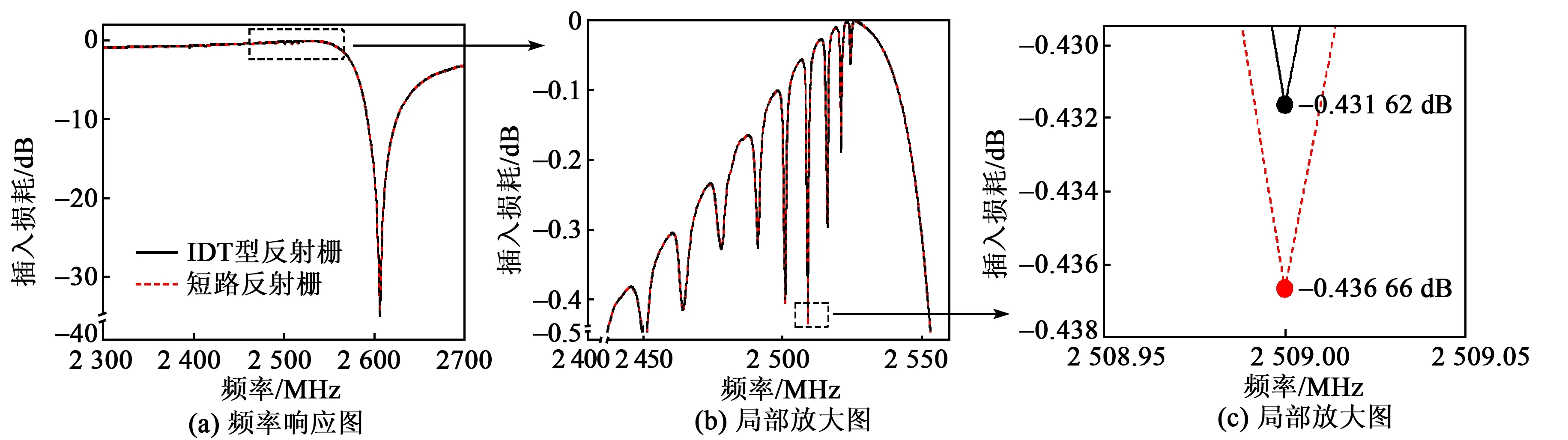
图10 IDT型反射栅对采取占空比和反射栅周期措施后的优化对比图

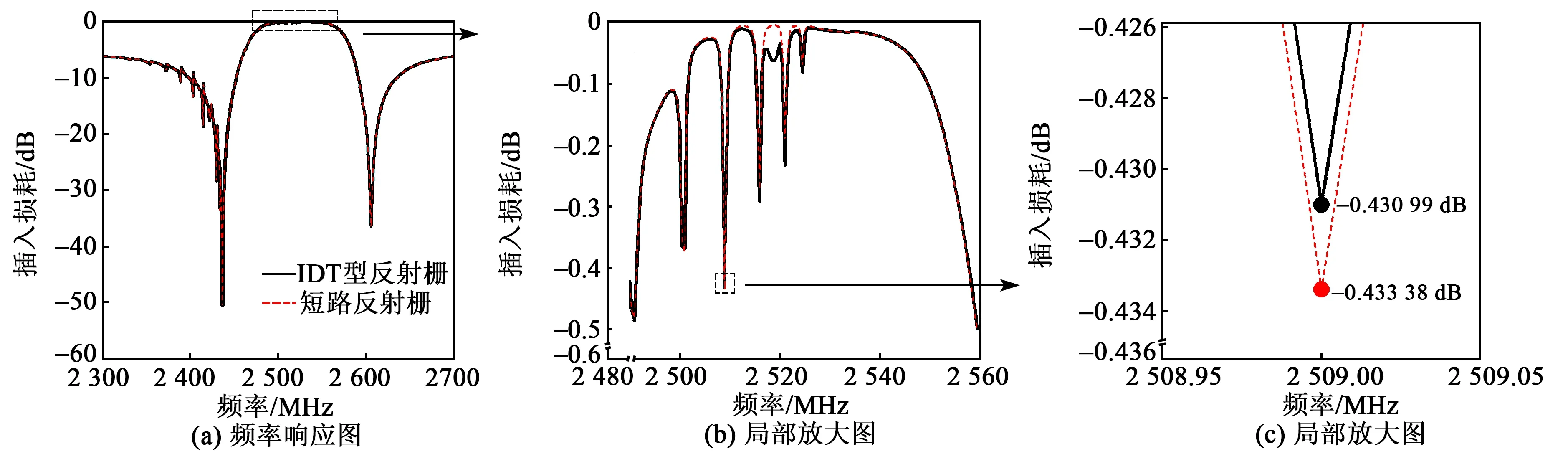
图11 采用不同反射栅结构的一阶梯形滤波器频率响应对比图

2.3 梯形拓扑结构的分析

常用梯形拓扑结构分为普通型和镜像型，其中镜像型的级间匹配较好。图12为不同拓扑结构的频率响应。由图可知，“π”型和“T”型镜像结构分别优化了普通结构通带左右边缘的凹陷问题，通带更平整。结合“T”型、“π”型结构的优点，器件采用两种结构相互级联而成的4阶“T+π”型镜像结构，如图13所示。图中S、P分别表示串、并联谐振器，P1、P2和S1、S2及P3、P4和S3、S4分别构成两个“π”型结构，P1、P4和S1～S4构成整体的“π”型结构；而P2、P3和S1～S4构成“T”型结构。设计时串联谐振器的叉指对数依次相差1～2对，以避免带内同一横向模式干扰随着级联阶数的增加而叠加。

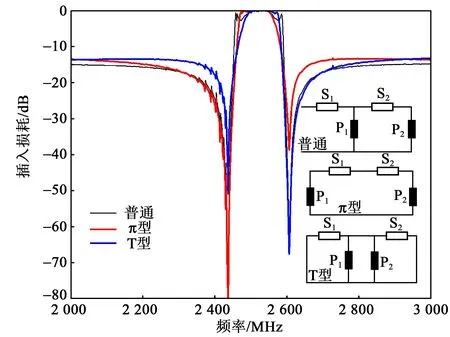
图12 不同拓扑结构的频率响应

图13 4阶“T+π”型结构和普通结构

综合以上设计和优化方法，最终设计的4阶梯形SAW带通滤波器的部分结构参数如表2所示。基于COMSOL的有限元仿真结果如图14所示。由图可看出，滤波器中心频率为2 520.5 MHz，插入损耗为-0.502 12 dB，-1 dB损耗带宽大于81 MHz，-3 dB损耗带宽大于98 MHz，纹波为0.646 89 dB，带外抑制大于30 dB。

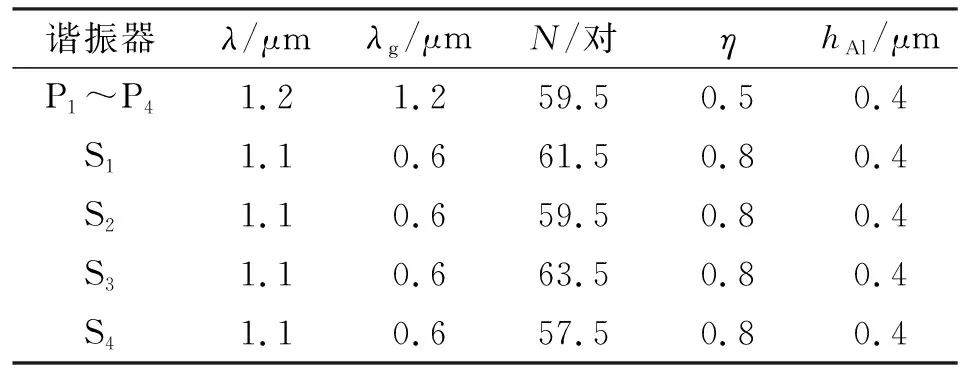
表2 器件结构参数

图14 器件仿真频率响应图

3 结束语

通过有限元结果表明，对于2.5 GHz左右的单层膜高频SAW滤波器，厚膜和非均匀电极结构有效地降低了器件的传播损耗。采用IDT型反射栅结构并通过调整反射栅周期，使带内最大尖峰损耗降低了43.49%，有效地削弱了带内由横向模式引入的尖峰损耗。最后通过级联不同叉指对数的串联谐振器，并基于4阶“T+π”型镜像拓扑结构设计的SAW带通滤波器的中心频率为2 520.5 MHz，插入损耗0.502 12 dB，带内波动为0.646 89 dB，带外抑制大于30 dB。