基于直觉模糊TOPSIS-GRA的地铁车站施工防汛应急决策研究

王心楠， 王军武， 刘一鹏

(武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070)

近年来随着全球变暖的加剧导致暴雨频发，再加上我国城市地下空间不断发展，使得大规模的地下空间建设在施工期面临一定的洪涝灾害风险。尤其是地铁车站工程，其施工场地通常在地表以下20～30 m处，雨水会自然汇入内部。施工现场一旦遭受到内涝灾害，其潜在的危险会对项目造成巨大的损失，严重时会危及城市的稳定运行以及居民生活[1]。同时由于地铁车站的施工涉及多个参建单位，施工专业多、项目多、环节多、接口多，作业时空交叉，组织协调量大，不同参与单位在内涝灾害中承担着不同的损失，各方都会制定各种应急决策方案。为了缓解甚至避免汛期洪涝灾害，在汛期到来时，地铁车站的项目管理人员进行科学合理的防汛应急预案决策具有重大意义。

目前国内外学者对应急预案的研究大致分为三类[2]：应急预案综合性研究、应急预案总体效果评价研究和针对某类具体应急预案的研究。近几年，国内学者针对地铁的应急预案研究大多是运营阶段的突发事件[3～6]，其中对地铁内涝灾害的研究大多从防涝风险评价[7,8]和脆弱性评价[9]上展开。但在施工阶段做好应急管理，可以将损失控制在最低限度以最大程度保证公众的生命财产安全，对项目的顺利实施起到了至关重要的作用。

另外，由于应急问题的复杂性、模糊性和不确定性，因此决策者得到的信息不完全，很难提供精确的数值进行预案评估。近年来，越来越多的学者将模糊集理论与多属性决策相结合来解决这一问题[1,10～15]。但单一的多属性决策方法都存在不同的缺陷，对应急预案评估时需要考虑将不同方法相结合以解决单一方法的缺陷。

鉴于此，笔者拟将直觉模糊集理论、TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)和灰色关联法(Grey Relation Analysis,GRA)相结合，构建地铁车站施工阶段防汛应急预案决策模型，以期为这类施工的防汛应急预案提供理论依据，对应急决策理论体系和评价模型进行一定的补充。

1 防汛应急预案评价指标体系

由于现有研究尚未建立能科学反映地铁防汛应急预案评价的指标体系，因此本文在构建指标体系时，首先考虑应急预案的编制原则、构成要素和内容等方面，然后再结合地铁车站汛期施工的特点和项目管理需要进行调整。

地铁车站建设期防汛应急预案的科学有效决策，集中在应急预案科学性和可操作性评价指标的选择上。此外由于地铁车站的施工阶段是一个动态过程，暴雨内涝灾害发生在不同施工阶段需要采取不同的应急措施，这导致项目管理人员无法提前编制可操作性强、内容详细完整的应急预案。同时，由于施工场地狭小、开挖深、环境复杂，应急救援的人员和设备不能无上限地进入，应急预案的制定要保证在救援时，应急措施可以有效开展，有序进行，同时要避免物资人力的浪费。

基于此，通过文献调查法、专家访谈法和问卷调查法[1,8,13,16]，本章选取应急预案编制的科学性、内容的完整性、经济性以及可操作性四个方面作为一级指标，筛选出16个二级指标构建地铁车站施工阶段的防汛应急预案指标体系，如表1所示。

表1 地铁车站防汛应急预案评价指标体系

2 地铁车站防汛应急预案决策模型

2.1 地铁车站防汛应急预案决策问题描述

2.2 确定专家权重

来自不同单位有不同的教育背景、经验(工作年限)、知识水平，这导致他们对于不同方案有不同的偏好。鉴于此，本文将专家的特点分为工作单位和自身优点两部分，按两部分特征指标进行打分汇总，得到各个专家的权重，准确描述了专家工作单位、学历、工作年限、知识水平等因素对权重的影响[1]。

当建设项目发生暴雨内涝灾害时，不同的参建单位承担着不同灾害损失，因此从减少损失的角度出发，承担损失越大的单位，专家意见的积极性和分项性越强，因此专家权重应越高。同时，不同的项目管理模式或不同的合同条款会让各方承担不同的灾害损失。因此，从工程管理学角度，在不同的项目管理模式下，不同参建单位的专家权重见表2。在表2中，承担最大风险单位的专家权重设为3，承担中等风险的单位设置为2，承担最小风险的单位设置为1。

表2 工作单位风险权重

项目实践中，由于教育背景、工作年限和知识水平等不同，不同专家对于应急预案的理解也不同。一般来说，学历越高、工作时间越长、知识水平越高的人，对应急预案的理解更加透彻，因此权重应越高。根据以往研究的结果，按照不同专家的个人特质进行打分，如表3所示。

表3 专家个人特质打分

通过上述分析，得到两方面五部分原始得分后汇总矩阵{Qk}其中k=1,2,…,s，则专家权重为：

(1)

2.3 构造集成的直觉模糊决策矩阵

由于汛期的不确定性导致做决策的时间很紧迫，决策者很难及时获得准确、完整的定量数据。因此，专家用“非常差、很差、差、稍差、中等、稍好、好、很好、非常好”的定性语言来描述每个指标的得分，通过直觉模糊数将这些语言转化为具体的数值[12]，如表4。

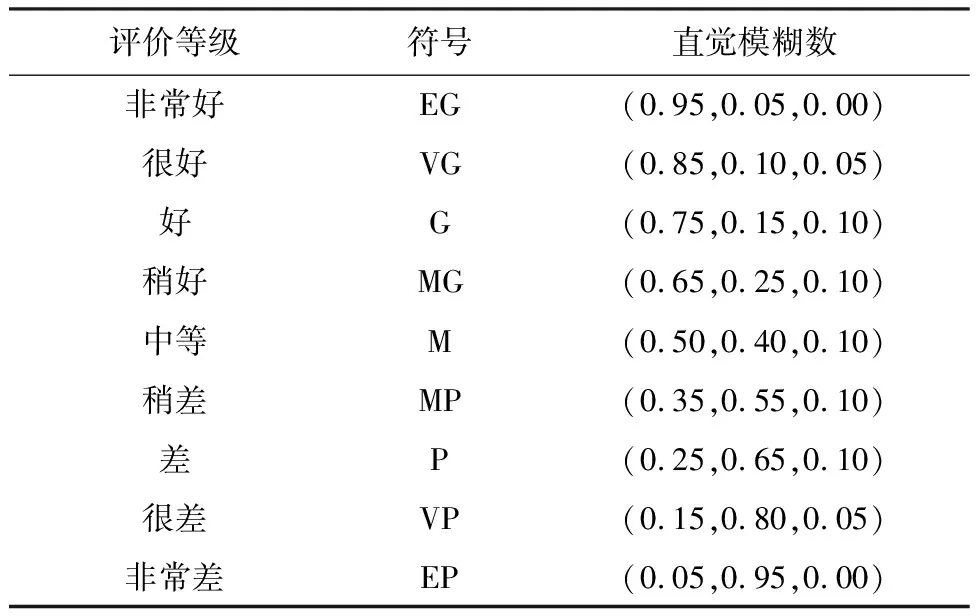
表4 语言变量转化为直觉模糊数

(1)对专家评价信息矩阵进行规范化处理

(2)

(2)构造集成的直觉模糊决策矩阵

在多目标群决策的实际运用中，为了保证决策信息的精确性以及实现对不同专家的评价信息进行有效集结，将决策信息通过直觉模糊加权平均(IFWA)算子集成，最终对所得具体实数进行排序优选，基本过程如下所述。

运用直觉模糊加权平均算子IFWA集结专家评价信息矩阵Rk和对应专家权重矩阵εk，得到综合评价信息矩阵T：

(3)

(3)计算评价指标权重

先计算直觉模糊熵值：

(4)

这里，如果uij=0,vij=0,πij=1，那么uijlnuij=0,vijlnvij=0,(1-πij)ln(1-πij)=0。

因此，指标体系第j个属性的熵权可以表示为：

(5)

2.4 TOPSIS-GRA方法求最优方案

要确定最优的应急决策预案，就必须科学地对所有备选方案进行综合评价。因为地铁车站施工防汛应急预案是在紧急情况下制定的，能获取到的汛期信息非常不充分，而TOPSIS法和灰色关联度法可以在有限条件下反映备选方案与正、负理想方案之间的位置距离和曲线形状相似度。但TOPSIS和灰色分析法在系统方案的整体评判上都存在一定缺陷[13]。因此，本文在方案评价决策中，构建了基于直觉模糊的TOPSIS-GRA评价模型，使评价结果更为科学、合理。具体步骤如下：

(1)确定正理想方案A+和负理想方案A-

(6)

(7)

式(6)和(7)中

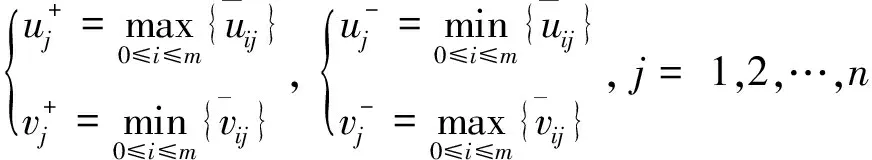
(8)

(9)

(3)计算备选方案Ai与正、负理想方案A+和A-的灰色关联度

(10)

(11)

式(10)和(11)中，

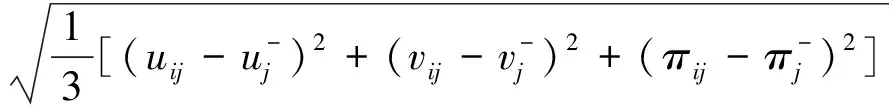
因此，可以得到灰色关联度为：

(12)

(13)

(4)合并欧式距离与关联度

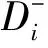
(14)

(15)

式中：α(0≤α≤1)为距离权重系数，反映的是决策者对距离的偏好程度，1-α(0≤1-α≤1)则体现了决策者对曲线形状的偏好程度，α的取值由决策者根据实际的决策问题、决策条件等具体情况而定。

(5)计算备选方案的相对贴近度向量S=(S1,S2,…,Sm)T，即：

(16)

根据Si的大小比较，Si越大说明贴近度越高，方案则为最优，反之则说明方案越差。因此选取Si值最大的应急预案作为最终的最优决策。

3 案例分析

3.1 工程概况

兰家沟车站是成都轨道交通6号线三期工程，施工现场周边多是农田和荒地，并且曾经多次爆发洪涝灾害的青兰沟穿过该车站，因此兰家沟车站具有较好的吸水能力和较差的排水能力，该项目的施工模式是BT施工总承包模式。

2018年7月6日，中国四川省成都市开始降雨，并且据当地气象台预报，兰家沟车站施工区域未来几小时暴雨持续性降临的几率很大。此时，兰家沟车站正处于主体结构施工的关键时期，现场有大量的施工人员、设备和建筑材料，一旦施工现场在暴雨期间没有得到很好的管理，将会造成巨大的人力物力损失。

因此各参建单位迅速组织起来依据实际情况制定了三个应急预案A={A1,A2,A3}，如表5所示。由于决策时间较紧急，调度的资源有限，项目管理组邀请了4名不同领域的专家(分别以e1,e2,e3,e4表示)来参与该项目的防汛应急预案决策，专家评审组4名专家的基本情况见表6。

表5 三种应急预案简介

表6 决策专家组基本情况

3.2 兰家沟车站工程的防汛应急预案评价

根据第2章给出的决策方法，本章节采用逐步分析的方法给出了案例分析的详细计算过程。

(1)收集评估信息并获得个人评价矩阵

(2)基于专家的信息构造直觉模糊决策矩阵

根据表6中4位专家的个人信息，参考表2和表3的打分制度，可以得到专家组的个人信息如表7所示。根据式(1)得到专家的权重向量ε=(0.2609,0.3043,0.1957,0.2391)T。

根据式(3)，运用直觉模糊加权平均算子IFWA将专家评价信息矩阵Rk与对应专家权重矩阵进行集结，得到直觉模糊决策矩阵T。采用式(4)(5)得到各指标权重，综合评价信息矩阵信息表和各指标权重计算结果如表8所示。

表7 专家个人信息及权重

(3)计算加权后的Euclidean距离

首先依据式(6)(7)，确定正理想方案A+和负理想方案A-，如表7所示。根据式(8)(9)得到方案A1，A2，A3与直觉模糊集正、负理想方案的加权Euclidean距离结果如表9所示。

(4)计算灰色关联度

依据式(12)(13)，计算备选方案Ai与直觉模糊集正理想方案A+和负理想方案A-的灰色关联度，如表9所示。

(5)计算贴近度

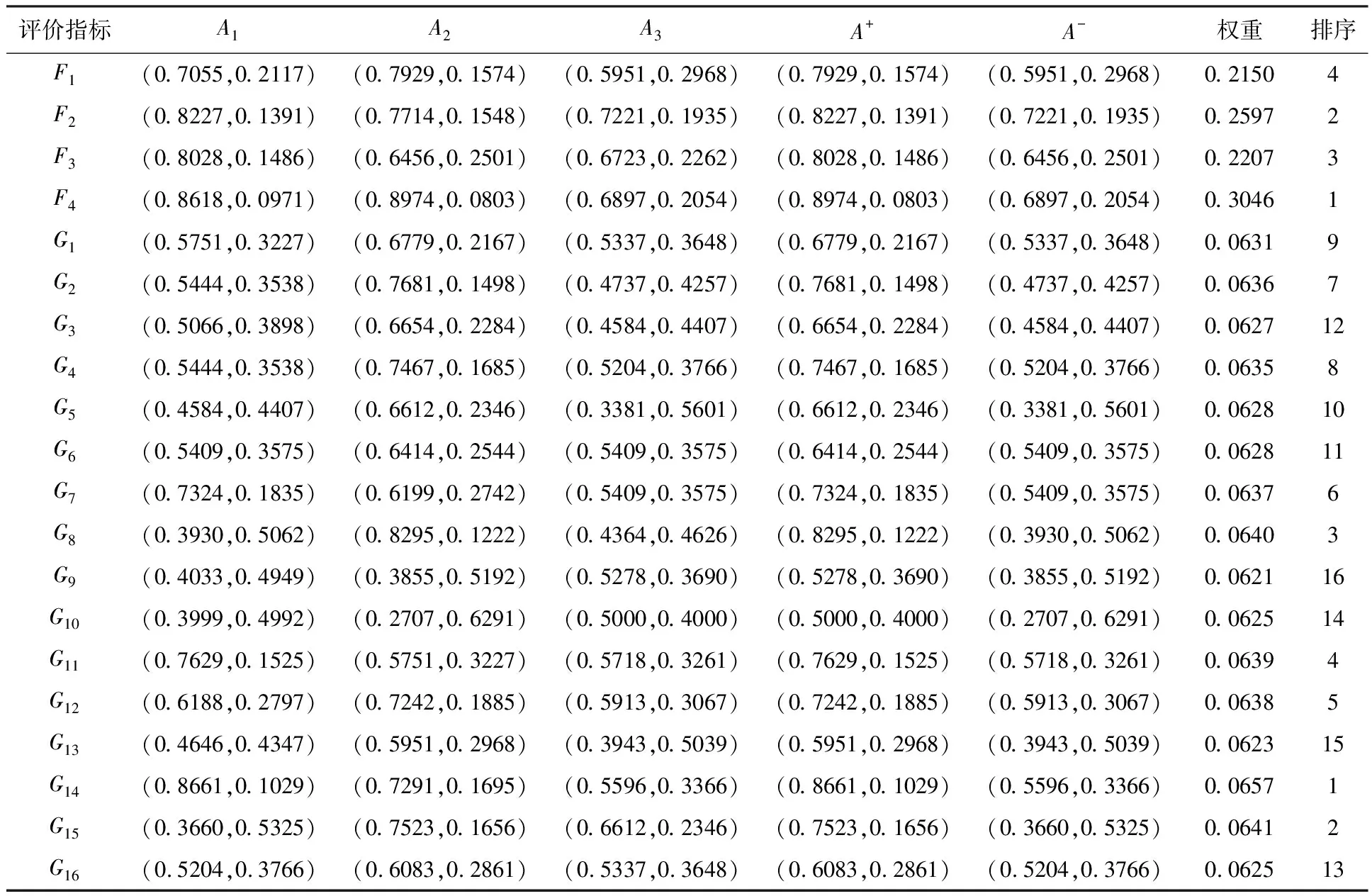
表8 综合评价信息矩阵信息、正负理想方案和权重

表9 备选应急预案到正、负理想方案的Euclidean距离、灰色关联度、贴近度

上述计算结果可以很容易地看出，相对贴近度的大小排序为：S2>S1>S3，因此兰家沟车站工程内涝灾害应急预案的优劣排序为A2>A1>A3，A2是兰家沟车站工程最优的应急预案。

3.3 应急预案决策结果分析

(1)在一级指标权重中，权重排序：F4可操作性>F2完整性>F3经济性>F1科学性；二级指标权重中，G14增加救援物资和人员的可行性和G15具有预警功能的综合权重较大，分别为0.0657和0.0641。由此可见，项目管理人员在编制类似项目的防汛应急预案时，应该首先考虑的是应急预案的可操作性，但是经济性会在一定程度上制衡，并且应急预案的重点要放在可以具有较强的预警功能，在执行措施时有增加人力物力的空间上。

(2)相对贴近度大小排序为：S2>S1>S3，因此兰家沟地铁车站工程此次防汛最佳应急预案是A2，该项目在汛期来临时应该立即停止现场的施工，撤离所有非救援人员，并向上级部门进行实时汇报。施工现场每一个易涝点增加2，3个水泵，青兰沟周边放置沙袋以提高周边的防洪能力，组织好后备力量。

(3)本文考虑到地铁车站施工的特殊性以及汛期的不确定性，认为专家的权重不应该默认相同，应根据具体情况进行讨论。因此将决策专家按不同的特征进行打分，再确定权重。这样利用了不同专家的优点，使决策结果更加科学合理。

(4)本文提出的一种基于直觉模糊的TOPSIS-GRA决策方法，解决了属性权重和决策者权重均完全未知且属性值以直觉模糊数形式给出的多属性群决策问题，与传统方法相比，该应急预案决策模型更加科学合理。

4 结 论

(1)采用文献调研法、专家访谈法，建立了初始的应急预案指标体系；考虑到地铁车站施工的特点以及汛期应急管理的要点，调整指标体系，通过两轮调查问卷建立最终地铁车站防汛应急预案指标体系。

(2)将直觉模糊集与多属性决策方法相结合，构建地铁车站防汛应急预案决策模型，直觉模糊集的隶属度、非隶属度和犹豫度，分别可以描述应急预案决策各指标的确定性、不确定性和犹豫性等信息。TOPSIS-GRA的方法解决地铁车站防汛应急预案信息获取不充分，不确定性和模糊性大的问题。兰家沟车站工程防汛应急预案决策结果与实际情况相吻合，证明了该决策模型的准确性和有效性。

(3)地铁车站汛期施工应急预案的编制要重视预案的预警功能，汛前各单位应该组织防汛应急救援演练，检验应急救援措施的可操作性，防汛物资和人员的储备是否充足以及增加人力物力的可行性。