超大地下结构施工期水位随机分布抗浮可靠性分析与应用

2022-05-13王海东尹鹏宇罗雨佳

土木工程与管理学报 2022年2期

王海东，尹鹏宇，罗雨佳

(湖南大学 a. 土木工程学院； b. 建筑安全与节能教育部重点实验室，湖南长沙 410082)

随着城镇化发展进程的推进，超大地下空间的开发利用已然成为主流，同时建筑物抗浮也面临着新的严峻考验。当下抗浮设计主要关注于项目在建成后的使用阶段，事故易发的施工阶段却研究甚微，施工期建筑自重未达到设计要求，自重小于水浮力时，就会发生抗浮失效，产生底板隆起、构件开裂等现象，甚至出现结构整体上浮，严重影响建筑物的安全性、适用性和耐久性。

近年来国内外学者对于抗浮问题的研究颇有深造。王海东等[1]例举了湖南某两小高层地下室抗浮失效事故，其主要原因为实际施工进度滞后，回填土未及时夯实导致抗浮失效；王静民等[2]提出抗浮失效的原因为地下室底板落在透水性较好的卵石层上，地下水位上升，产生很大的水浮力；李春平等[3]通过分析南京市某单建式地下室，提出在设计时未留足够的安全余量，抗浮验算时全额计入了上部平衡压重，未考虑施工期和使用期而导致的抗浮失效；施成华等[4]提出了施工阶段以排水量与时间的计算方法来实现动态降水，达到抗浮目的；徐春国[5]分别对多高层建筑地下室上浮的原因进行了分析，并介绍了锚杆抗浮加固处理的方法。已有研究逐渐开始关注施工阶段抗浮问题，但基于超大地下空间施工周期较长，容易在各种施工环境与过程中出现突发情况，现有设计和施工仍然缺乏灵活的预测及针对性措施。

目前已有不少学者将可靠性分析应用于工程结构分析中。宫凤强等[6]提出了工程结构可靠性的高阶矩方法；袁雪霞等[7]考虑了混凝土结构和模板支撑体系的主要失效模式，提出了施工期混凝土结构可靠度分析方法；贺广零等[8]提出了一种基于广义概率密度演化理论的动力可靠度分析方法；徐军等[9]基于概率密度演化方法评价了单层球面网壳结构的抗震性能；郭晓芳等[10]基于随机函数的降维思想对随机地震动作用下随机参数结构进行了抗震可靠度分析。显而易见，可靠性分析已经应用于工程结构分析的多个领域，在工程抗浮中所涉及的场地条件、地下水水位情况、工程结构本身的随机参数都具有很高的随机性，然而在已有研究中大多将这些随机条件作为确定性条件分析，忽略了其随机性，对工程抗浮问题的分析较为粗糙，导致抗浮事故频出。本文将可靠性分析用于抗浮问题中，利用ANSYS有限元软件中PDS模块对长沙某抗浮失效建筑进行建模分析，考虑施工过程中影响抗浮的几个因素，计算建筑在不同时期的可靠度，并引入一种更为高效的高阶矩可靠度算法，以此探讨可靠性分析对抗浮问题的实用性。

1 模型介绍

1.1 计算模型及参数

本文以发生抗浮失效的长沙市某住宅小区超大地下室工程为实例[11]，建立ANSYS模型；该项目为在建项目，为两层的地下钢筋混凝土结构，发生事故时所挖基坑未回填，地下室顶板尚未覆土；地表标高38.5 m，地下室底板设计标高为31.50 m，两层结构的层高均为3.8 m，地下室的建筑面积为27679 m2，抗浮设计水位为36.00 m；其平面图如图1所示；各层的梁柱截面信息及楼板厚度信息如表1所示，建模时不计入活载及除自重外恒载，将地下水位产生的浮力荷载视为均布荷载加载到地下室底板，设置水位为可变参数，通过式(1)将需要加载的均布荷载与水位关联。

P=rw(C-H+h)

(1)

式中：P为均布荷载(kN/m2)；γw为水的重度(kN/m3)；C为水位标高(m)；H为地下室底板标高(m)；h为地下室底板厚度(m)。

图1 结构平面

表1 各层梁柱截面尺寸及楼板厚度

1.2 抗浮桩的模拟

在模拟抗浮桩时考虑已发生抗浮失效的实际情况：在桩顶2 m范围内混凝土破坏，只考虑桩顶2 m范围内的钢筋受拉性能，不考虑混凝土的受拉性能，建模仅针对桩体中发挥作用的钢筋，采用Beam188单元来模拟钢筋，钢筋的弹性模量为200000 N/m2，屈服应力360 N/mm2；梁柱刚接在ANSYS中通过共用节点实现；楼板采用Shell63单元模拟，与梁共用轴线保证梁板的连接。

1.3 模型位移约束条件

结构平面图右侧的阴影部分为发生抗浮失效的区域，左边为主楼部分，在模型中用固定约束代替主楼对地下室的约束作用；桩底设置固定约束，模拟土层对桩的约束；建立的ANSYS模型如图2所示。

图2 已建好的ANSYS模型

1.4 模型验证

根据长沙某住宅小区发生抗浮失效的实际情况：抗浮失效发生在2017年的6月底到8月中旬，由现场水位的实测数据可以得知其变化主要分为四个阶段：第一阶段为6月20日起大量降雨带来的水位上升；第二阶段的转折为7月初，水位渐渐回落，但降水主要依靠现场的排水设备及自身的蒸发，由于底板以下为不透水层，排水量非常有限，并且周边的山体使得地表水继续汇入，致使现场水位未降至地下室底板以下，水位存在隐患；第三阶段为7月底的水位上升：7月底再次发生特大降水，现场水位呈现大幅度增长；第四阶段为8月中旬，已经发生抗浮失效，现场施工人员增强了设备排水并钻孔底板泄压，水位缓缓下降至底板附近，现场水位变化如图3所示。

图3 现场水位变化

课题组人员分别于7月17日与8月21日在现场进行两次实测，实测采用精密水准仪测量，实测中选取了底板构件标高的最低处作为基准点，其余各点减去该点的标高值来得到相对标高，由此得到底板的竖向变形数据；在ANSYS中利用荷载步按照水位变化逐步施加水浮力荷载，将计算得到的板的变形值数据与现场的实测数据作对比，以验证模型的合理性；实测数据与模拟数据对比图如图4，5所示，其中测点序号由a-r×a-1/n×a-3～a-16依次类推，所测数据为框架柱节点处的底板变形。

对比7月与8月的实测数据与模拟数据及变形云图，实测数值与模型中的模拟数值在各个测点的拟合较好；通过云图观察底板的变形情况，可以发现底板变形较大的区域均集中在a-r×a-1～a-m×a-9的区域中，且为上浮位移，a-k轴附近由于主楼约束的存在几乎不发生变形，模型变形情况与现场实测结果较为相符，因此该模拟可以较好地反映结构真实情况，可将ANSYS模型用于后续可靠度计算当中。

图4 现场实测与模拟数据对比

图5 现场实测与模拟云图对比

2 结构可靠性分析

2.1 参数选择

在本文抗浮可靠性分析中，将有关影响因素作为随机输入变量考虑[12]，可以分别从抗力及效应两方面考虑；抗力为结构的自重，在结构中影响自重的主要因素有：施工进度阶段、混凝土与钢筋的材料属性、梁柱板等构件的尺寸等；效应为地下室底板受到的水浮力作用，与现场的水位有关，由于施工期基坑未回填时，地表水与降水灌入基坑及地下水位上升导致现场水位较高，最高可达到地表标高38.5 m，根据现场实测将这一阶段水位分布统计数据定为截断高斯分布，均值为36.73 m，截断上限为38.5 m，基坑填埋及覆土后，水位有所降低，根据现场实测此阶段水位均值为33.51 m；使用期已满足设计要求，覆土及回填土已夯实，地表水无法灌入，水位较低，可选择一个水文年的地下水位统计数据，均值为31.24 m，最高可达到设计水位36 m；通过查找文献资料及进行大量数据实测统计，得到具有相同标准值的材料属性及构件尺寸等的变量统计特性，如表2所示。

2.2 可靠度计算

在工程结构可靠性分析理论中，根据结构工程要求和相应极限状态标志，可以建立结构的功能函数或极限状态方程；本文以抗力与效应来表达结构极限状态的数学公式如式(2)。

Z=g(R,S)=R-S

(2)

式中：S为荷载效应，表现为水浮力上浮效应；R为结构的抗力，表现为结构抗浮效应。由于抗力受材料属性及构件尺寸的影响，因此式(2)可进一步写为：

Z=g(R,S)=g(E1,v1,…,B1,H1,…,h)

(3)

令式(3)等于0，即Z=R-S=0得到结构的极限状态方程，极限状态方程用以表示极限状态面(或失效面)并将功能函数定义域Ω划分成为可靠域Ωr与非可靠域Ωf，当Z<0时，结构处于失效状态；Z=0时，结构处于极限状态；Z>0时，结构处于正常使用状态。

表2 基本随机输入变量分布

2.2.1 高阶矩法

矩法[6]首先通过随机变量的概率分布进一步计算得到功能函数的统计矩(若不特别说明，皆指中心矩)信息，再通过统计矩信息来拟合出概率密度函数，最终通过对所得概率密度函数进行数值积分得到失效概率及可靠度；相比于Monte Carol数万次的计算次数，矩方法在相同精度时只需数次计算即可，本文用高阶矩法进行计算，并与经典的Monte Carol[13,14]结果作对比，探讨高阶矩法是否可作为抗浮可靠性分析的一种简化算法。

采用高阶矩法时，重点在于统计矩的计算与概率密度函数的拟合；文献[15]中比较了几种求统计矩的方法，提出了改进的双变量降维方法来求统计矩可以保证计算的精度与效率，因此在本文中采用此方法计算统计矩；其次需准确地拟合概率密度函数以求得可靠度及失效概率，在文献[16]中详细地介绍了几种拟合方法并通过算例进行了比较，结果表明Pearson柔性系统分布法拟合得到的概率密度曲线与已有的经典分布的概率密度曲线具有较高的一致性，其他方法存在着或多或少的偏差，因此本文采用Pearson柔性系统进行拟合。

2.2.2 统计矩计算及概率密度函数拟合

首先根据文献[16]提出的改进双变量降维方法进行前四阶矩的计算；改进双变量降维方法在原有降维方法的基础上加了高阶无迹变换方法，弥补了难以兼顾精度与效率的不足；用改进的双变量降维方法表示的统计矩如式(4)。

(4)

式中：I[Zi]为Z的统计矩；H(θ)为θ的一个确定性函数，可由式(5)得到：

Z=G(X)=G(RN-1(θ))=H(θ)

(5)

式中：RN-1为Rosenblatt、Nataf或同分布变量之间线性变换的逆变换；θ为包含n个独立的标准正态随机变量，0为n维零向量，0-i1,i2表示去除掉第i1和i2个元素的零向量;0-j表示去掉第j个元素后的零向量，例如：当n=3时，i1=1，i2=3，则H(θi1,θi2,0-i1i2)=H(θ1,0,θ3)；式(4)中的第一项为二维积分，可以通过高阶无迹变换用9个积分点与权重表示，如式(6)。

(6)

式中的积分点可根据计算经验确定[15]。

式(4)中的第二项为一维积分，用3点高斯-埃尔米特积分可以直接求其解，如式(7)。

(7)

综上，统计矩的表达式可写为式(8)。

(8)

由双变量降维方法求得统计矩后利用Pearson系统拟合概率密度函数并计算失效概率，计算流程如图6所示。

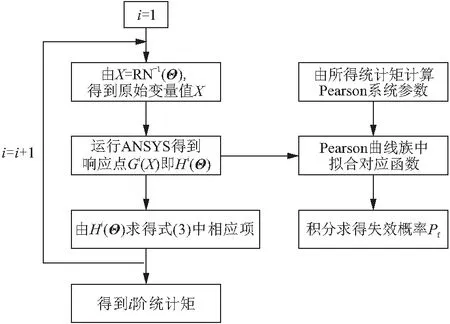
图6 高阶矩法计算流程

3 结果与分析

3.1 可靠性分析

本文在计算时选用抗浮桩拉断作为抗浮失效指标，即一次计算中存在有一根抗浮桩的轴力大于极限承载力，则视为结构抗浮失效，此问题在可靠性分析中可以表示为：将轴力中的最大值与极限承载力的差值作为随机输出变量，记为Z，即Z=Nmax-max(x1,x2,…,xn)。

本文对施工期与使用期进行可靠度计算，施工期按施工节点划分工况，共分为四个工况，分别是负二层完工、负一层完工基坑未回填、负一层完工基坑回填及覆土完成，分别计算结构的抗浮可靠度；当施工处于负二层时，考虑到地下室底板还未连成整体，各个底板之间由后浇带隔开，此时水位上涨时，上涨的水会通过后浇带等渠道排出，相当于对地下室做开孔排水处理措施，因此不考虑负二层完工阶段，而从地下室底板连成整体之后的负一层完工，水的浮力效应无法有效缓解的阶段开始考虑；负一层阶段时，根据实际情况考虑到负一层完工时未覆土且基坑未回填时的水位较高，对结构抗浮有较大影响，因此在负一层阶段还应考虑基坑未回填的工况。

应用高阶矩法与Monte Carol法计算所得的可靠度结果如表3所示，其中μz表示功能函数的平均值，σz表示功能函数的标准差，α3z表示功能函数的偏度系数，α4z表示功能函数的峰度系数。

由表3可知，随着施工进度的推进可靠度增大，失效概率减小，施工期三个阶段的可靠度指标均小于《建筑结构可靠度设计统一标准》[17]中的脆性破坏指标3.7，失效概率较大，易于发生抗浮失效，使用期可靠度指标为4.02，满足规范要求，可靠性分析结果与实际相符。施工周期较长，复杂的水文地质条件和气候条件导致现场水位变化复杂，而且在设计中缺乏对施工期针对性的抗浮设计，因此基于可靠度指标来评价施工期抗浮能力具有重要意义，在设计阶段时，可通过历史水位资料、预测水位及实测水位计算施工期可靠度，做出详细的施工期抗浮设计及抗浮措施，由此可以有效的避免施工期抗浮事故的发生。

表3 计算结果

对比Monte Carol与高阶矩法，两种方法的计算结果相对误差非常小，表明双变量降维结合Pearson系统的高阶矩法具有很好的精确度；比较两种方法的计算次数，高阶矩法仅仅需要N=4n2-2n+1=133次确定性计算便可得出与Monte Carol法107次计算接近的结果，高阶矩法也满足计算效率的要求；通过对比表明，文中所提的高阶矩法在此抗浮可靠性分析中有较好的适用性,可以作为简便算法使用。

3.2 敏感性分析

基于ANSYS平台利用CDA(Contribution Degree Analysis)[18]法对构件尺寸、材料属性及现场水位等随机输入变量进行敏感性[19]分析，分析结果如图7所示。

图7 敏感性分析

计算结果表明，影响最大的敏感因子是水位分布，构件尺寸及材料属性的影响较小，验证了可靠度与水位有映射关系，今后可重点关注水位分布的影响。

3.3 工程建议

对本文中工程实例的可靠性分析及敏感性分析表明，影响抗浮可靠性的因素主要为复杂的水位分布，其次是结构自身的材料属性及构件尺寸，

由此在实际施工及设计中提出几点建议：

(1)优化抗浮评价指标：本文分析结果表明用可靠度指标评价结构抗浮能力与实际相符，在工程中可以将可靠度指标作为预警指标指导设计与施工。

(2)加强对水位的监控：施工过程的周期较长，很容易受到周边水文地质及气候条件的影响，而结构抗浮可靠度与水位有较强的关联，在工程中应充分考虑水位的复杂变化，为抗浮可靠性分析提供足够的数据支撑。

(3)建立抗浮预警系统：基于可靠度指标与水位存在的映射关系，利用可靠性分析对大量水位数据进行计算，以可靠度结果定义预警水位，并建立预警水位与应急处理措施的映射关系；建立水位预测模型为安全施工提供施工前预测、施工中预警服务；施工前，通过预测长期水位，将长期水位与预警水位对比得到对应预警等级，为整个施工过程提供抗浮专项施工建议；施工中，基于短期的天气预报及可能存在的极端恶劣天气利用水位预测模型进行短期预测，对比预警水位，为当时的施工提供预警及应急处理措施；并在施工过程中将水位实时变化与预警水位对比，根据预警水位与应急处理措施的映射关系给出应急处理建议。