电动摩托车车架刚度与模态分析*

杨润泽 文少波 许屹洲 朱冠瑜 李潇雨

（南京工程学院汽车与轨道交通学院 江苏 南京 211167）

引言

电动摩托车车架承载着所有部件的质量，且在行驶过程中还受到各种载荷的作用。电动摩托车车架刚度是指车架结构抵抗弯曲变形的能力，对车架疲劳耐久性以及整车NVH 性能有很大的影响。同时车辆在行驶过程中，受到外在激励的情况下，如果外在激励与车架固有频率接近，会产生共振影响车架乃至整车的安全[1]。因此，本文拟对所设计的双摇篮式电动摩托车车架进行刚度与模态分析。

传统车架的设计需要进行试制和现场测试，存在投入资源多、研发周期长的缺点。随着计算机技术的发展，各种计算机软件已广泛应用于产品设计。在此采用CATIA 和ANSYS 软件相结合，综合CATIA的建模能力和ANSYS 的有限元分析能力，进行车架的刚度和模态分析，为新型电动摩托车的研发提供理论依据。

1 电动摩托车车架三维模型

在CATIA 软件中建立电动摩托车车架三维模型，对车架结构进行简化，重点突出对刚度与振动特性影响较大的部件。在结构简化的过程中，依据部件受力情况划分承载件和非承载件。保留位于较高应力区的承载件，如车架主管、支管、电动机上支撑管、发动机下支撑管、前撑管等。对于非承载件，如安装空洞、固定螺栓、车身套件等，适当合并或者去除。经过车架结构简化后，在CAITA 中建立的三维模型如图1 所示。

图1 电动摩托车车架三维模型

2 电动摩托车车架有限元模型

2.1 材料设置

进入ANSYS workbench，选择Static Structural 模块进行车架材料设置。材料采用Q235A，其主要属性为：弹性模量212 GPa、泊松比0.288、密度7 860 kg/m3、抗剪模量82.3 GPa、张力强度390 MPa、屈服强度235 MPa。

2.2 有限元模型的修整

电动摩托车车架由不同截面的钢管焊接而成，因此需要将在CATIA 中建立的几何模型导入ANSYS Geometry 模块进行清理，消除边界错位和车架弯管处的缝隙，压缩相邻曲面之间的边界，以提高有限元分析的效率和准确性。

2.3 有限元模型的网格划分

钢管管径和壁厚与构件长度相比很小，使用六面体实体单元虽然精度很高，但是网格划分困难、计算时间过长，因此对管件采用MultiZone 即多域扫掠型网格划分法，单元尺寸设为5 mm。划分后的网格如图2 所示，包含了2 052 个单元，4 088 个节点。

图2 车架有限元网格划分

3 电动摩托车车架刚度分析

车架刚度指标分为扭转刚度和弯曲刚度两种。车架的扭转刚度是指车架结构抵抗扭转变形的能力，弯曲刚度是指车架结构抵抗弯曲变形的能力，会影响整车轴距，进而影响整车的操纵稳定性。运用ANSYS workbench 模块对车架结构进行分析，得到车架扭转与弯曲时的位移与应力云图，以此作为校核车架刚度的依据[2-3]。

3.1 扭转刚度分析

在分析车架扭转刚度时，对车架与后悬架的4个连接点施加x，y，z 三个方向的平动自由度约束。在车头的转向立管的上下端点施加强制位移约束1 mm，通过模拟仿真分析与计算得出两端点的支反力。具体的约束如表1 所示。

表1 车架扭转刚度分析时的约束

经过车架扭转刚度仿真计算，在强制1 mm 的位移约束下，转向立管的支反力为908 N，两个力加载点的距离L 为180 mm。车架扭转刚度可由公式（1）得出[4]。

式中：Cr：扭转刚度，单位为N·m/rad；F：让端点强制位移Xmm 所产生的支反力，为908.72 N；L：转向立管上载荷加载点的距离，单位为180 mm；X1、X2：端点的强制位移量，单位为1 mm。

将上述参数带入公式（1）计算可得电动摩托车车架的扭转刚度为14 709.6 N·m/rad，高于摩托车车架扭转刚度所要求的指标11 000 N·m/rad。车架位移云图与应力云图如图3、图4 所示。

图3 扭转刚度位移云图

图4 扭转刚度应力云图

从图3 可知，最大位移量发生在左右前撑管上，大小为0.52 mm，位移量较小，因此对车架结构影响较小。

从图4 可知，车架整体应力水平不高，最大应力88.271MPa，发生在转向立管与前撑管连接处，此处为多个管件连接处，容易出现应力集中，并且由于转向立管受到方向向左的强制位移，所以产生了较大的应力。扭转引起的最大应力小于Q235A 的屈服极限，符合要求[5]。

3.2 弯曲刚度分析

在分析车架弯曲刚度时，将摩托车车架视为如图5 所示的简支梁，支点A 为转向立管上端点，支点B 为后悬架硬点。在简支梁中部施加作用力F，对前支点施加xz 方向平动自由度约束，对后支点施加xyz 方向平动自由度约束，就能够通过仿真计算得到车架所有位置的弯曲刚度。具体的约束如表2 所示。

图5 简支梁弯曲刚度计算参数示意图

表2 弯曲刚度分析时的车架约束

图5 所示刚度计算公式如下：

式中：EI：弯曲刚度，单位为N/m；F：集中载荷，单位为N；a：加载点到支点的距离，单位为m；x：测量点到支点的距离，单位为m；f：测量点挠度，单位为m；L：两支点间隔，单位为m。

经过车架弯曲刚度仿真计算，在F=1 000 N 的载荷下，测量点挠度f=0.04 mm，加载点到支点的距离a=0.2 m，测量点到支点的距离x=0.71 m，两支点间隔L=0.91 m。将数据带入公式（2）计算可得电动摩托车车架的弯曲刚度为184 652 N/m，高于摩托车车架弯曲刚度所要求的指标100 000 N/m。车架弯曲刚度位移云图与应力云图如图6、图7 所示。

图6 弯曲刚度位移云图

图7 弯曲刚度应力云图

从图6 可知，最大位移量发生在发动机支撑管与下横管处，大小为0.095 mm，位移量较小，因此对车架结构影响较小。

从图7 可知，车架整体应力水平较低，最大应力21.99 MPa，发生在上横管与边管连接处，此处为多个管件连接处，容易出现应力集中，所以产生了较大的应力。弯曲引起的最大应力小于Q235A 的屈服极限，符合要求。

4 电动摩托车车架模态分析

摩托车在路面上行驶时，路面的不平整度会对车架产生激振，当激振频率与车架某一固有振动频率相近时就会产生共振，严重影响电动摩托车的机械性能并有可能对车架结构造成破坏。

由于电动摩托车上的轮胎与悬架具有非线性特性，且在行驶过程中电动摩托车车架的实际边界条件极为复杂，因此采用自由边界条件，即自由模态分析[6]。

采用Block Lanczos 算法获取车架的模态参数，获得前12 阶固有频率和振型。因为是自由模态，前6阶固有频率为0，因此分析结果从第7 阶开始。通常车架结构的前几阶振动容易被激发，可以有效地表现车架的整体性能，所以取7～12 阶的模态分析结果来表达车架的振动特性，相应的固有频率和振型描述如表3 所示。

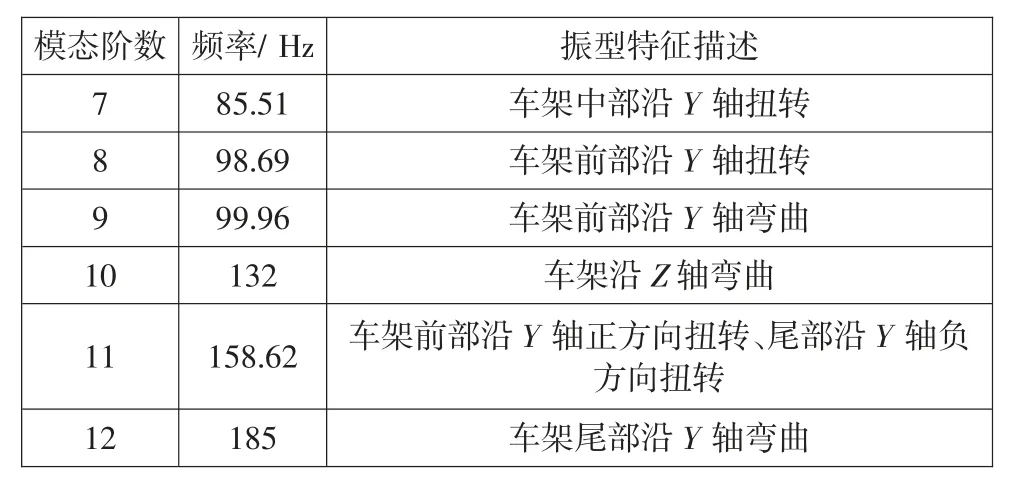
表3 各阶固有频率和振型描述

电动摩托车行驶时，会受到不平路面的激励而产生振动，即路面不平度激励[7]。当路面激励频率与车架固有模态频率相近时，车架产生共振，共振频率为

为了防止产生共振，车架结构的第一阶固有频率应大于路面激励所产生的最大频率，此时需要代入电动摩托车的最高时速为80 km/h，我国路面不平度波长为0.32 m。将数据带入公式（3）可求得车架即将发生共振时路面激励产生的最大频率为69.4 Hz。由表3 模态分析结果可知，车架的一阶固有频率为85.51 Hz，因此路面不平整度激励不会使车架产生共振。因此本文电动摩托车车架结构符合标准[8]。

5 结论

本文基于CATIA 对电动摩托车架进行三维建模，再将模型导入ANSYS workbench 模块对扭转和弯曲两种刚度进行了分析与计算，均达到了摩托车的刚度指标，驾驶性能良好。最后对车架进行了自由模态分析，选取了前6 阶模态分析结果，并通过计算证明路面不平度激励不会使车架产生共振，结构设计合理。为电动摩托车车架结构的设计、分析与计算提供了理论指导，缩短了电动摩托车的研发周期。