基于Duffing振子参数估计的伪码调相引信干扰信号设计
2022-05-13闫晓鹏王珂刘强郝新红于洪海
闫晓鹏, 王珂, 刘强, 郝新红, 于洪海
(1.北京理工大学 机电动态控制重点实验室, 北京 100081;2.北京宇航系统工程研究所, 北京 100076;3.中国兵器科学研究院, 北京 100089)
0 引言
伪码调相引信具有定距精度高、抗干扰能力强等优势,在舰载低空导弹、地空导弹等精确制导弹药上逐渐得到广泛应用[1-2]。由于伪码调相引信具有较强的抗干扰能力,传统的预置波形干扰难以对其实现高效率干扰[3-4]。为此常采用重构式欺骗干扰,即先搜索、截获引信信号,对引信信号进行分析、估计,从而构造合适的干扰信号,在引信工作频率上实行欺骗干扰[5-6]。
现有文献对伪码调相引信信号的参数估计主要有两类:一是估计引信载频信号参数;二是已知载频或其他参数估计伪随机序列。文献[7-9]分别基于循环谱密度、2阶循环统计和随机共振3种方法估计载波频率和伪码码率,但是无法计算伪随机序列。文献[10]提出了一种同步解调的伪随机序列估计方法,但需要先对载波频率进行精确估计。文献[11-12]基于循环谱密度函数进行伪随机序列估计,但需已知码片时宽和载频。上述估计方法中,仅有载频信息无法重构出干扰信号,而对于伪随机码的估计需要先验知识,或需要额外的计算从而耗时较久,难以满足引信干扰系统对实时性的要求,且在低信噪比下性能较差,无法适用于实际战场的复杂电磁环境,因此也不能完全满足干扰信号重构的要求。
由于Duffing振子对噪声的免疫力以及对特定频率周期信号的敏感性,在微弱信号检测领域有广阔的应用前景[13-15]。本文在混沌理论基础上,提出具有低信噪比和高估计精度特性的Duffing振子参数估计方法,避免了传统伪码调相引信信号估计方法对信号载频等先验信息的高度依赖性,在超低信噪比下基于Duffing振子的参数盲估计结果仍能重构出有效的干扰信号。仿真和实验结果表明,基于Duffing振子参数估计重构的干扰信号效果明显优于传统的周期调制干扰信号。
1 伪码调相引信基本原理
由于m序列伪随机码容易产生、规律性强,具有许多优良的性能,伪随机码体制引信通常应用m序列。利用m序列产生器产生的伪随机序列的数学表达式[16]为
(1)

伪码调相引信发射信号为经过伪随机序列0/π调相后的射频连续载波,其数学表达式为
s(t)=Ap(t)cos (ω0t+φ0)
(2)
式中:s(t)为伪码调相引信发射信号;A为发射信号幅值;ω0为射频载波频率;φ0为信号的初始相位。(2)式表示用1和-1形式伪随机码对载频幅值进行调制来实现0/π相位调制,将其表示为相位形式,则有
s(t)=Acos (ω0t+φ0+φi)
(3)
式中:φi为伪码调相信号相位编码,
(4)
伪码调相引信信号具有很强的抗干扰能力,传统的干扰方法很难对其实施有效的干扰,侦察- 重构的欺骗性干扰通过捕获和估计引信参数,重构出与引信信号相似度极高的干扰信号,对引信实施欺骗性干扰。从(3)式中可以看出,伪码调相引信信号的参数主要由载波频率ω0和相位编码φi两个成分组成。若能对这两个参数进行有效的估计,则可重构出该引信信号,从而实现对该引信的有效干扰。
2 基于Duffing振子参数估计的伪码调相引信干扰原理
为了实现对伪码调相引信重构式干扰波形的设计,需要先对该引信信号的载频和相位编码进行参数估计,本文提出基于Duffing振子的参数估计方法。
2.1 基于Duffing振子的参数估计方法
2.1.1 Duffing振子微弱信号检测模型
Duffing方程具有较为简单的表达式和结构,当其受不同类型和不同参数的信号驱动时,其系统输出的相轨迹表现出鲜明各异的特性,可利用这些状态特性进行微弱信号的检测。Duffing振子微弱信号检测系统[17-18]可表示为
(5)
式中:x为位移;y为速度;-ax(t)+bx3(t)为非线性恢复力,a、b均为大于0的正实数,称为系统参数;Fcos(ωt)表示幅值为F、角频率为ω的周期内策动力信号;Acos(ω0t+φ0)为外部待测信号,此时为一般的正弦信号;n(t)为随机扰动。Duffing振子在k=0.5、a=b=1时有明显的混沌状态[19-20]。用Δω表示待测信号和内策动力信号之间的频率差,即|Δω|=|ω0-ω|。系统存在临界阈值Fc:当F
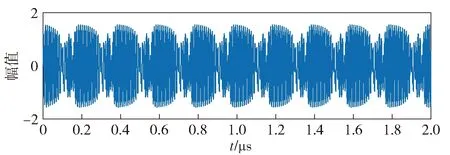
图1 普通正弦信号激励的Duffing振子输出时域图Fig.1 Time-domain diagram of Duffing oscillator output excited by ordinary sinusoidal signal
2.1.2 伪码调相信号激励的Duffing振子检测模型
当Duffing振子受伪码调相信号激励时,其检测模型可表示为
(6)
类似于正弦信号,先令F=Fc,则系统处于临界混沌状态。如果忽略噪声,则总的内策动力信号可表示为
Fccos (ωt)+Acos (ω0t+φ0+φi)=
a(t)cos (ωt+Φ(t))
(7)
式中:
(8)
(9)
φ(t)=φ0+φi。因为待测微弱信号的振幅远小于内策动力信号的振幅,即A≪Fc,所以Ф(t)可以被忽视,且
(10)
如果Δω=0,则由(10)式可以看出,由于φi的影响,等效幅值a(t)和Fc的大小关系不断变化,从而导致Duffing振子输出在混沌态和大尺度周期态间不断转换,且其变化与φi的变化一致。其状态如图2所示。因此,当已知载频时,可以根据Duffing振子的输出状态直接得到伪随机序列。
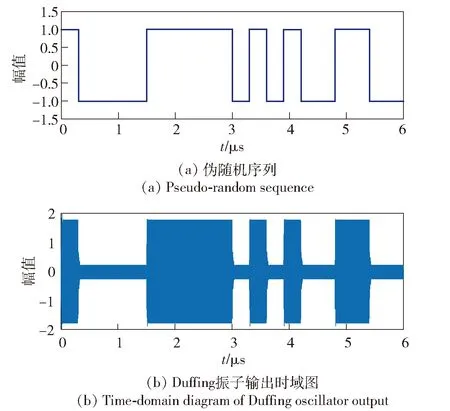
图2 Δω=0时伪随机序列与Duffing振子输出Fig.2 Pseudo-random sequence and Duffing oscillator output for Δω=0
当0<|Δω|≤0.03ω时,由于待测信号相位的不断变化和载频不一致的影响,伪码调相引信信号激励的Duffing振子的间歇混沌状态虽然有一定规律性,但与正弦信号有所不同,也不再与伪随机序列一一对应,其时域图如图3所示,其中各项参数与图1中的正弦信号一致。
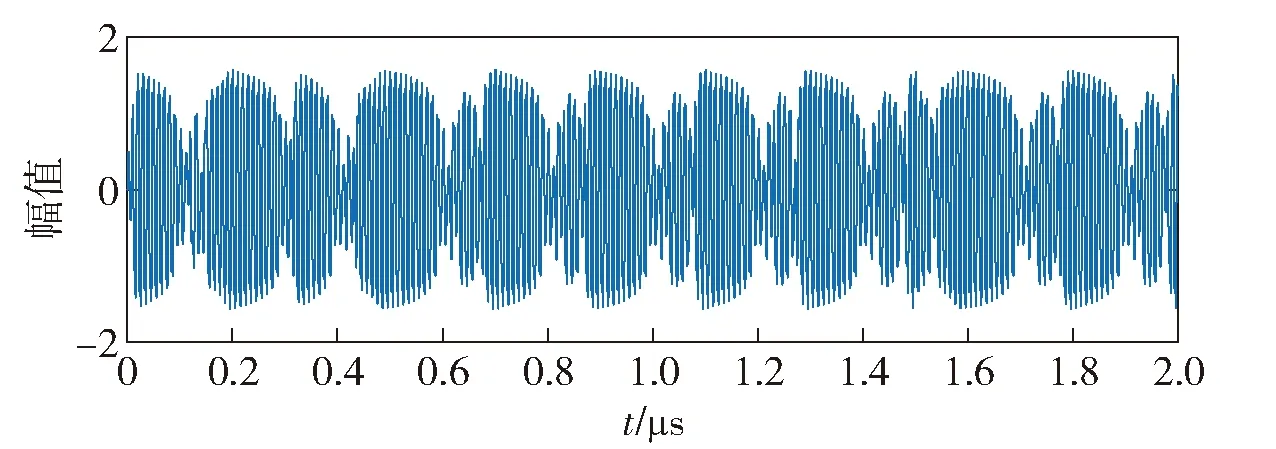
图3 伪码调相引信信号激励的Duffing振子输出时域图Fig.3 Time-domain diagram of Duffing oscillator output excited by pseudo-code phase modulation fuze signal
2.1.3 伪码调相信号激励的Duffing振子输出特性
由(10)式可以得到
sgn (a(t)-Fc)=sgn (cos (Δωt+φ(t))),
(11)
式中:sgn(数值)表示符号函数,如果数值>0,则sgn=1,如果数值=0,则sgn=0,如果数值<0,则sgn=-1。根据(11)式,伪码调相引信信号通过Duffing振子后并没有一个稳定的间歇混沌周期,信号在某一时刻所处的状态由相位调制码φi和差频Δω共同决定,即Duffing振子输出信号与相位编码φi、差频余弦函数cos(Δωt+φ0)之间具有乘法关系,具体表示为
sgn (a(t)-Fc)=sgn (cos (Δωt+φ0))×cosφi
(12)
由(12)可知:当系统处于大尺度周期态时a(t)>Fc,则sgn(a(t)-Fc)=1;当系统处于混沌态时a(t)≤Fc,sgn(a(t) -Fc) =-1或0.因此可以对Duffing振子的输出状态进行二值化处理,得到Sys(t),
(13)
对伪码调相引信信号与Duffing振子内策动力信号的差频取余弦,并进行二值化处理,得到Df(t):
(14)
对接收的伪码调相引信信号的相位编码进行二值化处理,得到伪随机序列Pc(t):
(15)
因此(12)式可转化为
Sys(t)=Df(t)×Pc(t)
(16)
由于Sys(t)、Df(t)和Pc(t)均为只有1和-1的二值函数,(16)式的等效形式为
Df(t)=Sys(t)×Pc(t)
(17)
Pc(t)=Df(t)×Sys(t)
(18)
综上,Sys(t)、Df(t)和Pc(t)3种信号之间若是知道其中二者,第三者即可通过(16)式~(18)式得到。
2.1.4 基于Duffing振子隐含周期性的伪随机序列和载频估计方法
根据2.1.3节中得到的乘法关系式可知,伪码调相引信信号激励的Duffing振子系统输出信号已知,若能够根据Duffing振子系统输出信号的特性得到载频和伪随机序列的任意一项参数估计值,则另一个参数可由乘法关系式求出。
如图4所示,根据红色虚线的标注,虽然Sys(t)没有表现出直接的周期性,但是在其看似无规律的数值改变之中隐含了Df(t)的周期。如果在一个Df(t)周期内,仅存在有限次由Pc(t)引起的Sys(t)数值改变,则将这几次数值改变所经历的时间求和,即可得到一个Df(t)周期T=2π/|Δω|。Sys(t)每一段1或-1状态保持时间的长度可标注为1~16(相同的长度不再重复标注),而2+3+4,2+5+6,2+7+8,2+9+10,2+11+12,2+13+14,2+15+16(2表示所有与标注2时间长度相等的部分)等时间和正好为一个Df(t)周期。首先计算出Sys(t)每一段幅值为1或-1时该状态保持时间的长度,随后将每相邻两段、三段和四段的时长相加(分别为T2i、T3i和T4i),在3×10-5s时间内统计得到相邻不同段数的点数,结果如图5所示。由于本文设置Δω=2π×3×106rad/s,采样频率fd=1×1012Hz,则周期T的点数为3.333×105。由图5可以看出,虽然存在一些T2i和T3i不足一个周期或超出一个周期的情况,但从统计上,T2i和T3i的点数值基本与Df(t)的周期T对应的点数值相等或接近,而T4i与周期T的点数值相差较大,因此Df(t)的周期T可以根据T2i和T3i求取,这就是Duffing振子的隐含周期性。因此,舍弃T2i中小于0.95×T3min的值(T3min为T3i的最小值),对剩余的T2i求平均,即可得到Df(t)的周期T。
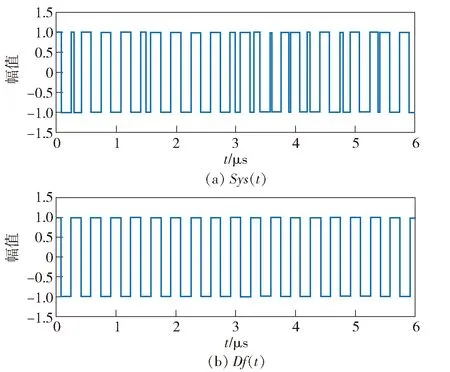
图4 Sys(t)和Df(t)的时域波形图Fig.4 Time-domain waveforms of Sys(t) and Df(t)
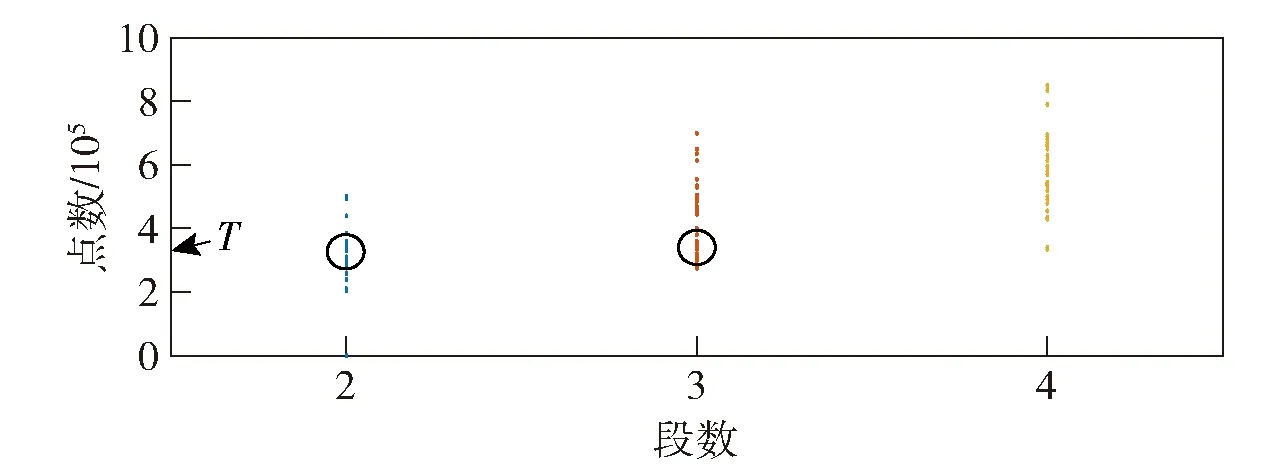
图5 Sys(t)中相邻段数的点数统计图Fig.5 Statistical diagram of the points of adjacent segment in Sys(t)
由于隐含周期T=2π/|Δω|,先令Δω>0,则根据Δω=2π/T得到频率差Δω,随后构建出与Df(t)具有相同周期的二值信号Df0(t),
(19)
根据(14)式和(19)式,Df(t)与Df0(t)相差一个初始相位φ0。根据求到的隐含周期T,在Sys(t)信号中找到正好满足相邻两段相加的长度为隐含周期T的位置,选择其中一段,令其起始点为t0,将其作为参考,则φ0满足
(20)
式中:q为任意整数,选择q值使Df0(t)右移φ0,通过补偿相位得到重构信号Dfrc(t),即可实现所述差频信号的重构。值得注意的是,在k值取奇数或偶数时,得到的Dfrc(t)可能与Df(t)相差半个周期,换言之Dfrc(t)= -Df(t)。如果将重构信号Dfrc(t)代替Df(t)与Duffing振子系统输出码Sys(t)相乘,则得到的伪码序列也满足Pcrc(t)=-Pc(t)。而伪码调相引信通常采用在相关之后采用检波、比较的方式确定是否起爆,因此即使Pcrc(t)=-Pc(t),对于伪码调相引信造成的干扰效果是一样的。因此在对Df(t)进行重构时,无需考虑q的奇偶。由于一般Df0(t)信号构建时都是从时间0开始的,q只需要满足qT/2>t0即可。
此前先令Δω>0,为判别Δω的符号,可以采取多路内策动力频率不同的Duffing振子同时进行参数估计的方式,每路Duffing振子对应得到相应的差频绝对值,通过比较相应的差频绝对值大小,再结合不同的内策动力信号频率,判断出频率差值Δω1,Δω2,…,Δωm的正负,m表示Duffing振子的个数,进而得到载频ω0=ω+Δω的估计值。
2.2 干扰信号重构
基于Duffing振子参数估计结果,可构建得到的伪码调相引信干扰信号sj(t)为
sj(t)=Ajpj(t)cos (ωjt)
(21)
式中:Aj为干扰信号幅值;pj(t)为估计得到的伪码调相引信的伪随机码;ωj为估计得到的引信载频。
引信接收到的干扰信号可表示为
sj(t)=Ajpj(t-τj)cos (ωj(t-τj))
(22)
式中:τj为预定随机时延。
由于本地延时τd未知,为确保干扰信号与引信本地延迟信号相关,从而使引信启动,在设计干扰信号时,干扰信号可以以一定步长不断改变延时τj,则引信接收到的干扰信号可以表示为
(23)
式中:Δt为转发延迟步长;n为延时个数;N为设置的转发延迟次数。
引信接收到的干扰信号与本振信号混频并滤除谐波后,得到的含有伪随机码的视频输出信号经过视频放大后可表示为
(24)
式中:AI为视频输出信号的幅度;ωd为多普勒频率。
将该信号与经过伪随机码延迟器延迟τd后的信号在相关器中进行相关处理,可以得到
(25)
由于cos(ωdt-φ0)在积分时间内为缓慢变化信号,可以视为常数,则(25)式可以表示为
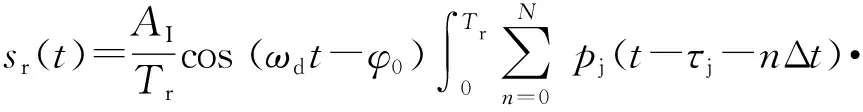
(26)
式中:R(τd-τj-nΔt)为盲估计的伪随机码经转发延时后与引信本地伪随机码的相关函数。
由(26)式可以看出,在干扰信号作用下,伪码调相引信相关器输出为估计出的伪随机码与引信本地伪随机码互相关函数经不同延时后的叠加与多普勒信号的乘积,当干扰信号延时与本地固定延时一致时,即τd=τj+nΔt时,相关器的输出最大。当相关器输出满足设定条件时,干扰信号能够突破引信的相关检测,对引信产生有效的干扰。
3 仿真验证
3.1 基于Duffing振子参数估计方法仿真
对于2.1节中设置的伪码调相引信信号,基于本文提出的Duffing振子隐含周期性仿真实现伪随机序列及载频的估计,且为了验证低信噪比下该检测方法的有效性,通过调节高斯噪声方差σ2来实现不同信噪比下的伪码调相信号检测。设置伪码调相信号幅值为0.01,调整σ2分别为0.000 5、0.005 0、0.050 0和0.158 1,对应信噪比SNR分别为-10 dB、-20 dB、-30 dB和-35 dB. 在这种条件下,基于Duffing振子隐含周期性得到的载频估计结果如表1所示。由表1可知,在-35 dB信噪比下,基于隐含周期性的伪码调相信号参数估计方法仍可以实现高精度的载频估计。
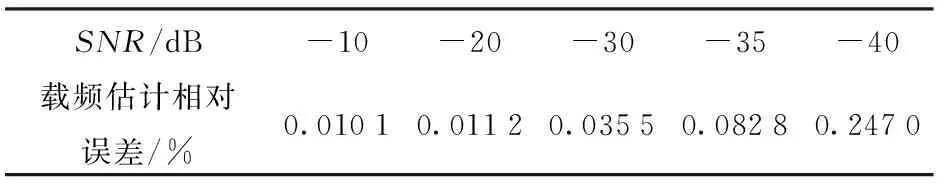
表1 不同信噪比下载频估计仿真结果
得到差频后,还需要与Sys(t)相乘得到伪随机序列。在伪码调相信号参数估计中,使用伪随机序列与原序列的互相关函数峰值与原序列自相关函数峰值的比,即相关相似系数,来表征伪随机序列的估计准确程度。表2所示为不同信噪比下基于Duffing振子隐含周期性和已知载频两种方法得到的伪随机序列与原序列相关相似系数。由表2可见,基于Duffing振子隐含周期性的盲估计方法,在 -35 dB 超低信噪比下估计得到的伪随机序列与原序列仍具有较好的互相关性能(相关相似系数>0.9)。该方法的估计性能非常接近已知载频的情况,且打破了需要先验知识的限制,因此有更好的实用性。
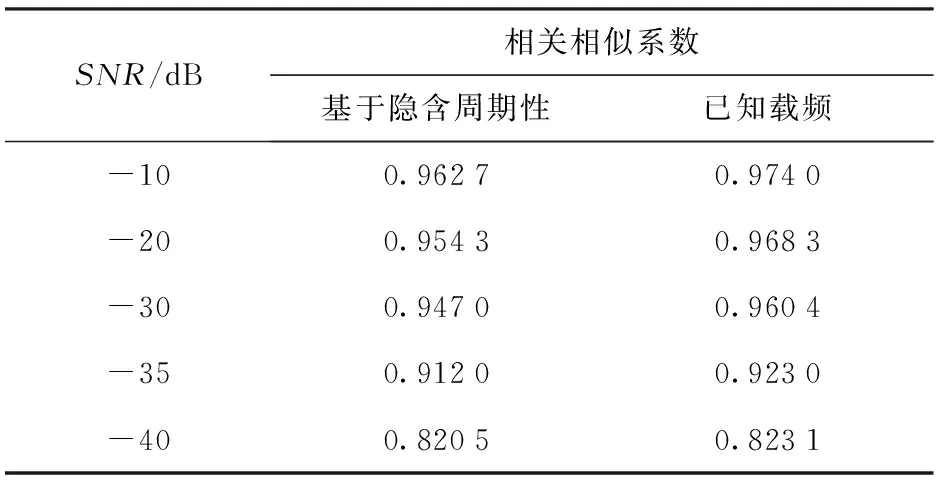
表2 不同信噪比下伪码序列相关相似系数仿真结果
3.2 干扰效果仿真
得到伪随机码和载频的参数估计结果后对干扰信号进行重构,将-20 dB信噪比下重构的干扰信号对引信实施干扰,得到的引信相关器输出信号波形如图6所示,其中图6(a)为目标回波作用下的引信相关器输出及启动信号,图6(b)为基于Duffing振子参数估计的重构干扰信号作用下的引信相关器输出及其启动信号。从图6中可以看出,在重构干扰信号作用下,引信可以启动并且相关峰可以完全覆盖目标回波信号作用下引信相关器输出的相关峰,能够对引信产生有效的欺骗性干扰。
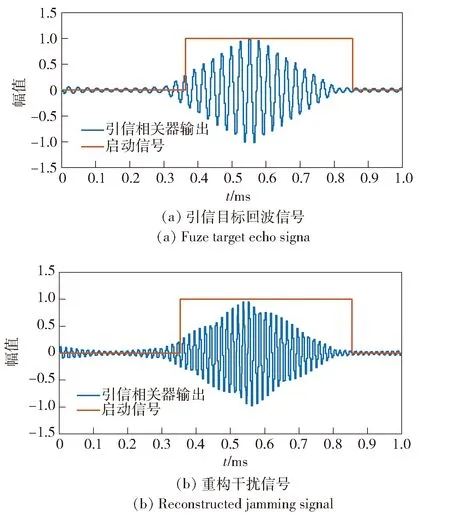
图6 不同信号作用下引信相关器输出Fig.6 Outputs of fuze correlator under the action of different signals
为验证基于Duffing振子参数估计的重构式干扰波形相比于传统干扰波形的有效性,仿真采用方波调幅信号、正弦波调幅信号、正弦波调频信号对伪码调相引信实施干扰,不同干扰信号在相同干扰功率下对伪码调相引信的干扰效果如图7所示。对比图7与图6的结果可知,在相同干扰功率条件下,传统干扰波形下引信相关器输出信号幅值很小,不能达到引信设置的阈值而不能正常启动。此外,求取不同干扰信号作用下引信输出信号与回波信号作用下引信输出信号的相似性系数,并与文献[22]所提出的基于3阶相关函数法进行参数估计和重构的干扰方法进行了对比分析,结果如表3所示。由表3可以看出,基于Duffing振子隐含周期性方法进行参数估计并实现重构式干扰作用后,引信相关器输出信号与回波信号作用下相关器输出信号之间的相似性系数高于典型周期调制的干扰信号,因此能够获取更好的欺骗式干扰效果。
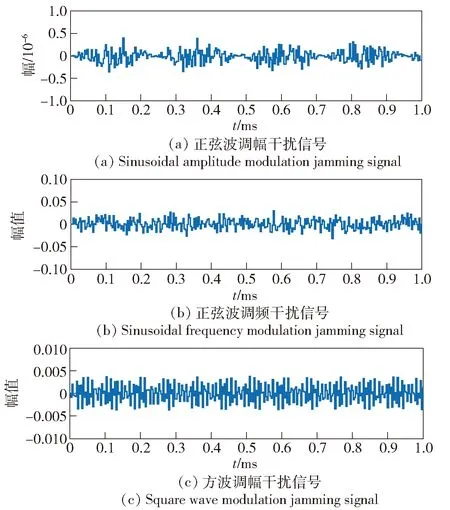
图7 不同干扰信号作用下引信相关器输出波形Fig.7 Outputs of fuze correlator under the action of different jamming signals

表3 不同干扰信号作用下相似系数仿真结果
4 实验验证
为实现基于Duffing振子的伪码调相引信干扰信号验证,建立半实物仿真实验系统,利用伪码调相引信样机发射信号,通过天线进入数据采集系统,经下变频后输入计算机;在计算机中进行载波和伪随机序列的估计,参数估计的结果传入干扰信号生成系统;干扰信号经射频信号源进行上变频并发射,再经天线进入引信样机,观察其检波和启动信号,检验引信是否启动,从而实现对引信干扰效果的验证。
为了对比不同干扰方式对伪码调相引信的影响,将各个干扰波形在相同实验条件下对伪码调相引信进行干扰,调整干扰信号的功率,找出能够使引信启动的最低干扰功率,结果如表4所示。由表4可知,基于Duffing振子隐含周期性进行参数估计的干扰信号使引信启动的最小干扰功率最低,仅为-1.3 dBm,具有最优的干扰效果,与仿真分析的结论一致。

表4 不同干扰波形作用下引信启动最小干扰功率
5 结论
为能够在低信噪比环境下提高对伪码调相引信的干扰效率,本文提出基于Duffing振子参数估计的伪码调相引信干扰信号设计方法。在建立Duffing振子输出信号、引信信号的伪随机码信号、引信信号与Duffing振子内策动力信号差频信号的乘法关系式的基础上,结合Duffing振子的隐含周期性,实现了引信载频和伪随机序列的盲估计并基于估计结果重构了引信干扰信号。得出主要结论如下:
1)基于Duffing振子的参数估计算法能够在超低信噪比下人具有较好的性能。
2)基于本文方法重构的干扰信号与传统引导干扰信号相比与引信目标回波信号具有更高的相似度,干扰效率更好。
