基于可射击概率约束的防空作战火力优化分配

智洪欣， 赵鹏， 李中， 彭祥新， 鲁旭阳， 王琛

(陆军炮兵防空兵学院郑州校区， 河南 郑州 450052)

0 引言

火力分配(WTA)作为防空作战中的一个重要环节，能够依据作战任务、战场实时态势及武器装备性能等因素，将空中来袭目标合理地分配给各防空火力单元，实现作战效益最大化。因此，WTA问题是关系到作战效能的决定性因素之一。

WTA问题主要涉及两个步骤：一是综合各种战场因素进行数学建模，构建合理的目标函数和约束条件；二是根据构建的数学模型，采用合适的最优化方法进行最优化计算。其中，数学建模是核心，最优化计算是关键。针对这两个步骤，已有大量研究，取得了丰硕成果。

文献[2-5]提出了以联合毁伤概率最大为目标的WTA模型，但是该模型忽视了火力资源消耗情况，在追求联合毁伤概率最大的同时易造成火力资源浪费，致使防空系统无法提供持续有效的防空作战能力。针对这一问题，文献[6]在传统模型中引入了联合毁伤概率均值，即将联合毁伤概率除以分配的火力单元总数，以尽可能少的火力资源消耗取得满足阈值的联合毁伤概率。文献[7]构建了一个多目标优化模型，同时将最大联合毁伤概率和最小分配火力单元数作为目标函数进行优化。文献[8-10]通过设置约束条件限制拦截同一目标的火力单元数，尽可能减少火力资源消耗。文献[6-10]单纯从数量上限制火力资源消耗，未考虑目标距离所分配火力单元射击区的距离，即未考虑目标到火力单元的飞临时间，生成的分配方案易贻误战机。针对该问题，文献[11]提出一种基于先期毁伤准则的WTA模型，在保证联合毁伤概率的前提下，以尽量少的火力资源消耗优先拦截飞临时间短的目标。文献[2-11]分别提出了基于不同约束条件最大化联合毁伤概率的WTA模型，然而这些模型都忽略了一个事实：只有在防空武器对来袭空中目标可以射击的前提下，计算联合毁伤概率、约束火力资源消耗、约束目标飞临时间等才有实际意义。

另外，WTA问题本质上是整数型非线性组合优化问题，属于一种NP难问题，目前常用群智能优化算法求解。文献[2]采用遗传算法求解WTA问题。文献[11]提出了一种混沌和粒子群混合优化算法，以提高算法的全局搜索能力。文献[12]改进了布谷鸟算法，引入了移民算子和柯西变异算子等，采用贪婪方式逐维更新，以提高算法的局部和全局搜索能力。综合分析这些算法，都不同程度地存在易陷入局部最优值、收敛速度慢或者算法设计复杂、实现困难等问题，不能满足战场实际要求，有待进一步提升。Faramarzi等受控制容积质量平衡物理现象的启发，提出了一种新的智能优化算法，平衡优化器(EO)算法。该算法控制参数少、鲁棒性强，易于实现，在多个标准函数测试中表现出较高的优化性能。然而，该算法未能有效平衡全局搜索与局部搜索能力，在一定程度上限制了算法的收敛速度，且增大了寻得全局最优值的难度。

针对以上问题，本文提出一种基于可射击概率约束的WTA模型，该模型在基于先期毁伤准则模型的基础上，引入了基于空袭强度和火力单元转火时间的可射击概率约束，从而使模型更贴近战场实际。在此基础上，提出一种非线性自适应惯性权重的改进EO算法。该算法首先采用Tent映射方法代替原算法中的随机方法初始化种群，实现种群多样性；其次，在位置更新公式中引入非线性自适应惯性权重，来平衡算法的全局搜索和局部搜索能力，加快收敛速度、提高求解精度。

1 基于可射击概率约束的WTA模型

假设在某次防空战斗中有批来袭空中目标，编号为(=1,2,…,)，进入个火力单元的责任防区，编号为(=1,2,…,)。令表示决策变量，其含义为：若分配火力单元拦截来袭空中目标，则=1，否则=0；令表示火力单元拦截来袭空中目标的毁伤概率，为火力分配方案对目标的联合毁伤概率，则

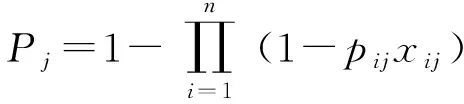
(1)

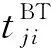
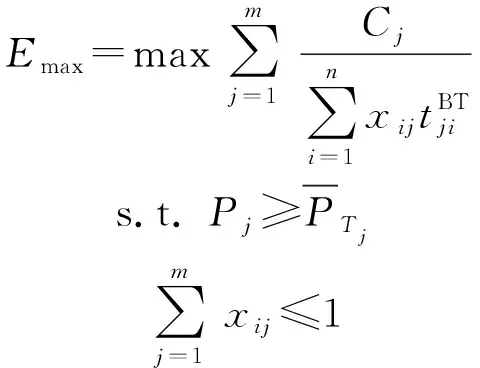
(2)

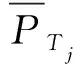
该模型在确保满足联合毁伤概率阈值的前提下，以尽量少的火力资源消耗，优先分配威胁度大、飞临时间短的目标。但是，该模型忽略了联合毁伤概率只有在火力单元对来袭空中目标可以射击的前提下才有实际意义的事实。因此，本文提出一种基于可射击概率约束的WTA模型。

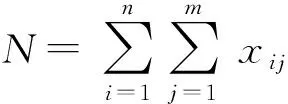
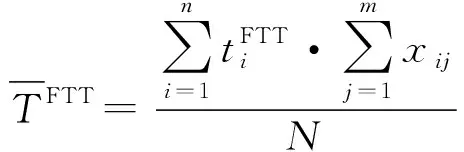
(3)

令表示空袭强度，根据排队论中的爱尔兰公式可得分配方案的可射击概率为

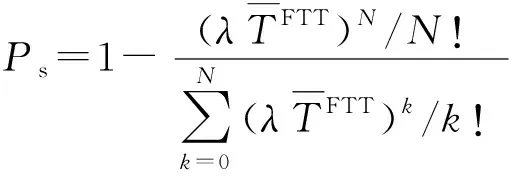
(4)

则基于可射击概率约束的WTA模型为

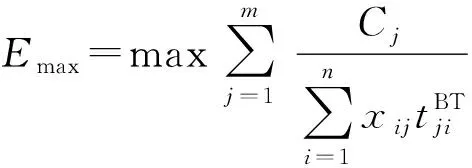
(5)

式中：为可射击概率阈值，可由指挥员根据战场态势确定。

从(5)式中可以看出，该模型保存了原基于先期毁伤准则模型的优势，即在满足联合毁伤概率阈值的前提下，以尽量少的火力资源消耗，优先分配威胁度大、飞临时间短的目标。同时也引入了基于空袭强度和火力单元转火时间的可射击概率，使联合毁伤概率计算具有实际意义，使模型更贴近战场实际。

由于(5)式带有非线性约束，在最优化计算过程中属于求解有约束的优化问题，本文采用罚函数法将其转化为一个求解无约束优化问题，设计罚函数如下：

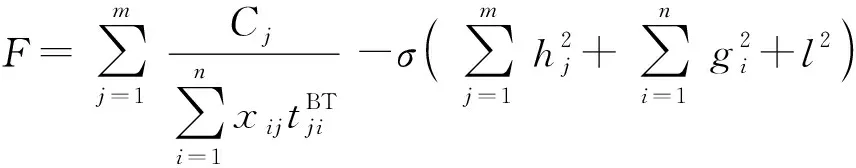
(6)

式中：为罚参数，表示惩罚的力度，开始为一个较小的正数，随着迭代次数逐渐增加到一个很大的值。

因此，把求有约束的优化问题转化为如下求解无约束优化问题：

(7)

(7)式是一个无约束优化问题，求得的最优解会使、和为0，因此(7)式的最优解是(5)式的最优解。

2 基于非线性自适应惯性权重的EO算法

2.1 标准EO算法

EO算法是一种模拟环境工程中控制容积完全混合(流入和流出控制体积的体积流量相同)的质量动态平衡物理现象(质量衡算)的智能优化算法，将控制容积内的浓度作为问题的解。

完全混合的质量动态平衡常用质量平衡方程描述为

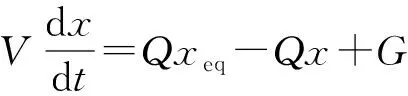
(8)

式中：为控制容积；为控制容积内的浓度；为流入、流出控制容积的流体体积；为平衡状态(控制容积内无质量生成)下的浓度；为控制容积内的质量生成速率。

(8)式描述了控制容积中质量流入、流出和生成过程中动态平衡的内在机理，对该1阶微分方程求解，可得

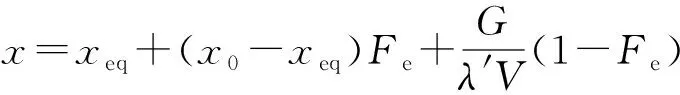
(9)

式中：为控制容积在时刻的浓度，即初始浓度；为指数项；′为流动率。

EO算法将(9)式进行优化改造后作为解向量更新公式，改造后的公式为

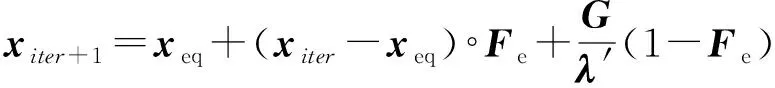
(10)

式中：为迭代次数；为当前解；为全局最优解；+1为更新后的解；′表示取值范围为[0，1]的随机数向量。

算法将当前4个最优解(,,,)以及它们的均值()组成平衡池：={,,,,}，在迭代计算中，(10)式中的全局最优解以相同概率从平衡池中选择，增强了算法的全局搜索能力。

为加强算法的局部搜索能力，算法将质量生成速率设计为

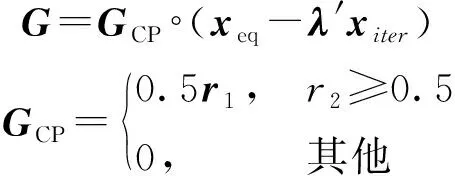
(11)

式中：为生成速率控制参数；为取值范围为(0，1)区间的随机数向量；为(0，1)区间的随机数。

同时为了平衡算法的局部搜索和全局搜索能力，改造为

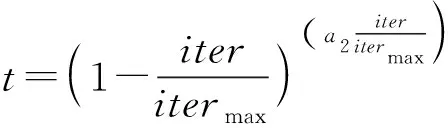
(12)

式中：为控制全局搜索能力的常系数，设置为2；sign(·)为符号函数；为取值范围为[0，1]的随机数向量；为最大迭代次数；为控制局部搜索能力的常系数，设置为1，EO算法通过和平衡全局搜索和局部搜索能力。

2.2 基于混沌序列的初始方法

有研究表明，初始种群对智能优化算法的优化效率有较大影响，分布均匀、多样性好的初始种群可以提高算法的收敛速度乃至提高算法的求解精度。然而，EO算法采用在搜索空间内随机生成的方式产生初始种群。这种随机生成的方式容易导致初始种群分布不均匀、多样性差。针对这一不足，本文提出使用Tent混沌映射产生初始种群，增强种群的多样性，从而提高算法效率。

Tent混沌映射的数学表达式为

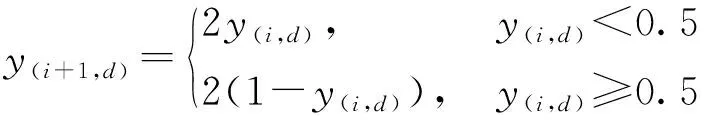
(13)

式中：为生成的混沌序列；为种群数量；为解的维度。

利用Tent混沌映射产生初始种群的主要思路是：首先根据(13)式生成混沌序列，然后将生成的混沌序列线性映射到解空间作为算法的初始种群。Tent混沌映射具有较好的遍历均匀性和随机性，因此使用Tent混沌映射产生的初始种群可以提高优化算法性能。

2.3 非线性自适应惯性权重

通常，智能优化算法在初期侧重于全局搜索，以便快速到达最优解附近；在后期则侧重于局部搜索，在最优解附近进行精确搜索。因此，算法性能在很大程度上取决于平衡全局搜索和局部搜索的能力。EO算法主要通过指数项来平衡，然而从解更新公式(10)式中可以看到，只作用于后两项，算法完全继承了最优解，仅依靠并不能有效平衡算法的局部搜索能力和全局能力。因此，本文提出在解更新公式(10)式中引入非线性自适应惯性权重，作用于最优解，与指数项配合共同协调算法的局部搜索和全局搜索能力，从而提高算法的性能。

基于非线性自适应惯性权重的解更新公式为

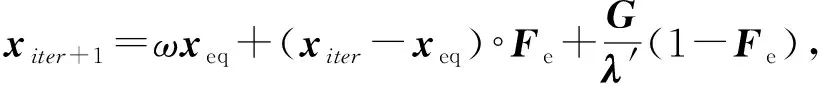
(14)

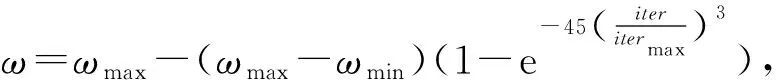
(15)

式中：和分别为惯性权重的初值和终值，本文设置为09和04，则随迭代次数的变化曲线如图1所示。

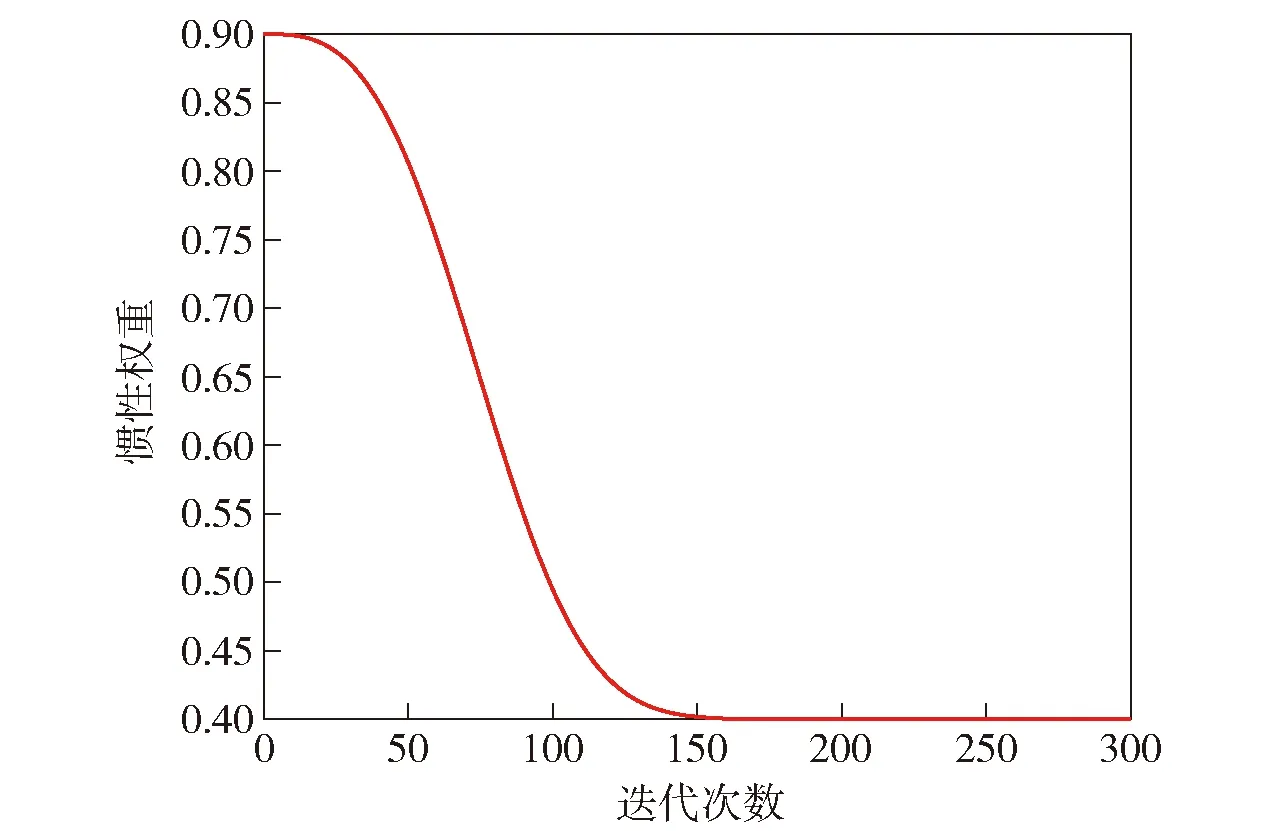
图1 惯性权重变化曲线Fig.1 Change curve of inertia weight

从图1中可以看出，惯性权重是迭代次数的非线性递减函数，在迭代初期和迭代末期递减速度相对较慢，从而使算法在迭代初期的一段时间能够保持较大的惯性权重，增强了算法全局搜索能力；在迭代后期的一段时间保持了较小的权重，增强了算法的局部搜索能力。由此可见，非线性自适应惯性权重提高了算法平衡局部搜索和全局搜索的能力，进而提高了算法的性能。

本文提出的改进EO算法流程图(见图2)主要步骤如下：

种群数量，迭代次数，解的维度；

全局最优解以及相应的适应度值。

初始化参数，=2，=1，=09，=04，=1，=-inf，=-inf，=-inf，=-inf

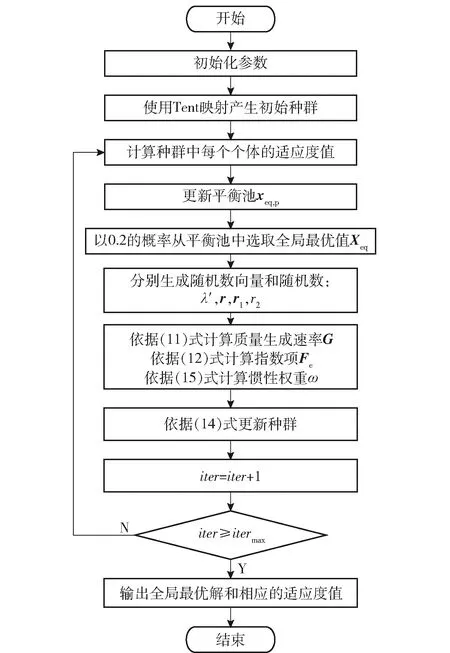
图2 基于非线性自适应惯性权重的EO算法流程图Fig.2 Flow chart of EO algorithm based on nonlinear adaptive inertia weight

使用Tent映射在解空间内产生初始种群。

计算种群中每个个体的适应度值。

比较适应度值，计算并更新平衡池：

={,,,,}。

以02的概率从平衡池中随机选出全局最优解

分别生成随机数向量′、、和随机数

依据(11)式计算质量生成速率，依据(12)式计算指数项，依据(15)式计算惯性权重

依据(14)式更新种群。

=+1

判断是否达到最大迭代次数，若达到则停止计算，输出最优解以及相应的适应度值；否则，转步骤3。

3 算例仿真计算及结果分析

为验证本文基于可射击概率的WTA模型的优点，以及所提基于非线性自适应惯性权重EO算法的有效性，进行算例仿真计算。

3.1 仿真设置

仿真配置为Intel(R) Core(TM) i7-6700 CPU，8 GB内存，Windows 7操作系统，利用MATLAB 2019b软件进行仿真计算。

假设在某次防空战斗中有8批来袭空中目标，进入10个火力单元的责任防区，各个目标的威胁度为=[060 070 035 056 081 076 066 083]，目标到火力单元的飞临时间为

各火力单元对来袭目标的毁伤概率为

各火力单元的转火时间为

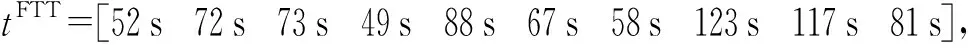
空袭强度设置为与来袭空中目标数相同：=8架min；预期联合毁伤概率阈值设置为08，可射击概率阈值设置为07，种群数设置为30，最大迭代次数为300

3.2 仿真计算结果及分析

3.2.1 模型有效性验证

分别基于本文提出的基于可射击概率约束的防空火力分配模型(以下简称Model 1)以及文献[11]提出的防空火力分配模型(以下简称Model 2)，使用改进的EO算法进行火力优化分配，分配结果如表1、表2所示。

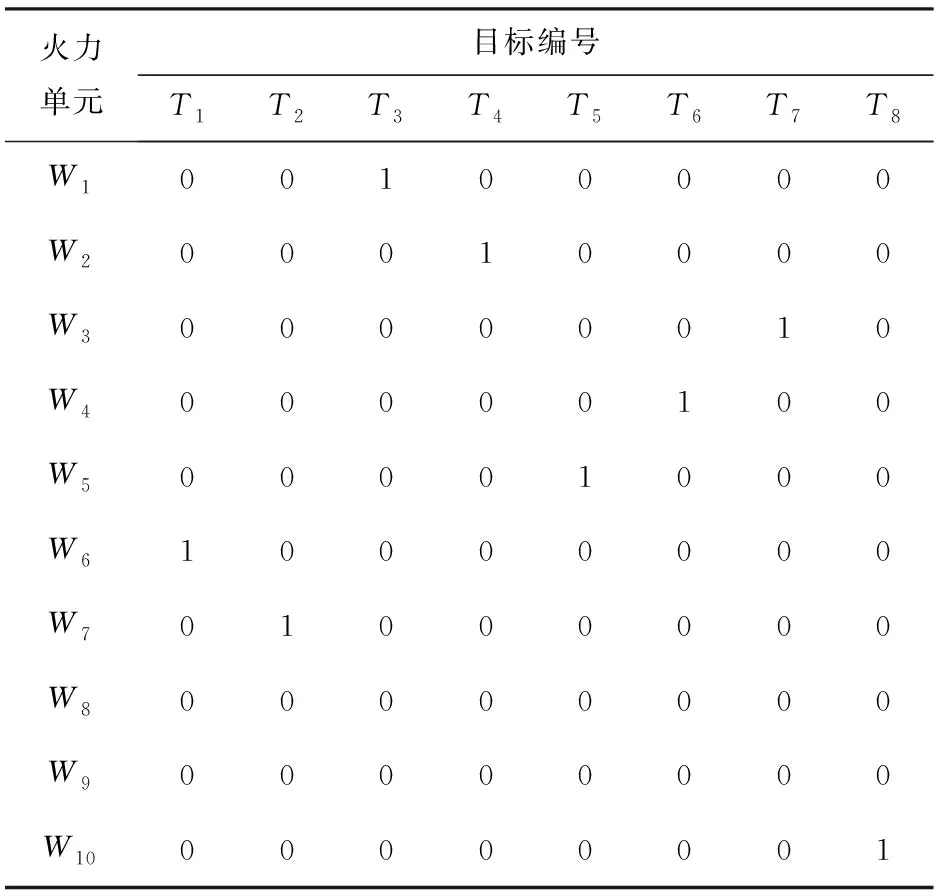
表1 Model 1的分配方案

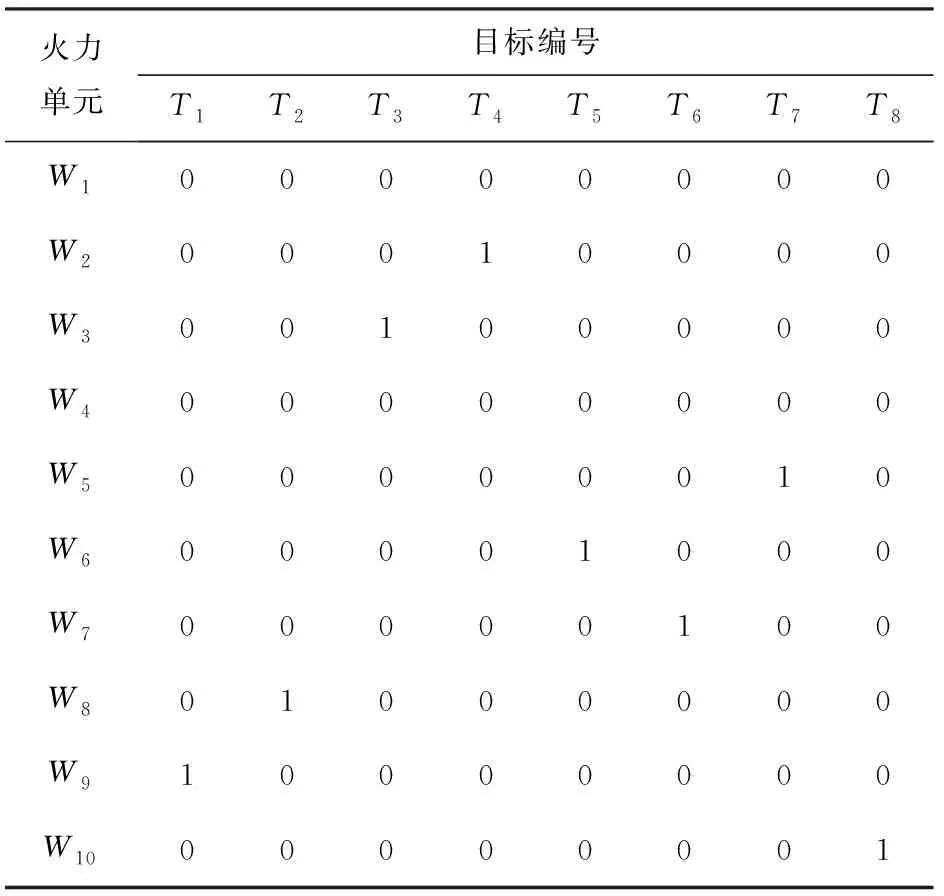
表2 Model 2的分配方案

从表1和表2中可以看到，Model 1和Model 2均能够约束火力资源消耗，分别选用8个火力单元拦截来袭的8个目标，节约火力资源，为防空系统提供持续作战能力。两种分配方案的联合毁伤概率和性能分别如表3、表4所示。

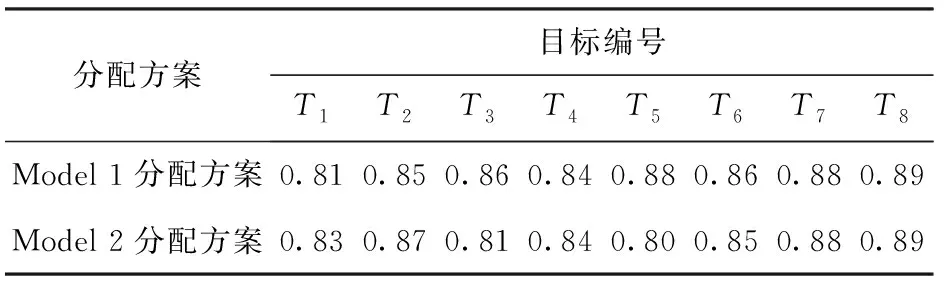
表3 分配方案联合毁伤概率

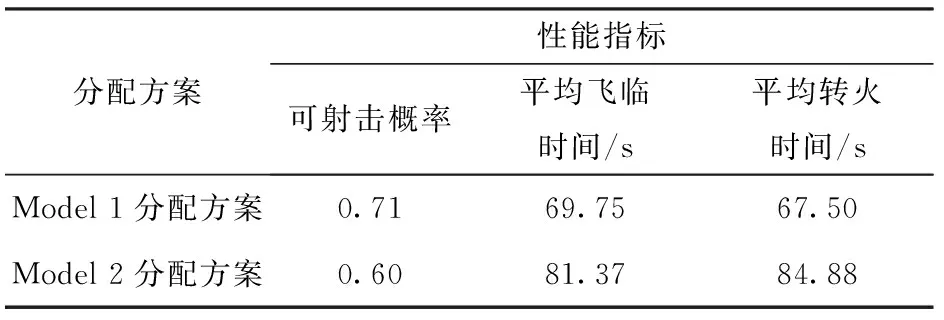
表4 分配方案性能

从表3中可以看到，两种模型的分配方案均满足设定的联合毁伤概率阈值0.8. 从表4中可以看出：Model 1分配方案的可射击概率为0.71，满足指挥员设定的阈值要求，但是Model 2分配方案的可射击概率为0.60，没有达到设定的阈值；Model 1分配方案的平均飞临时间和平均转火时间均比Model 2分配方案的短，表明Model 1在可射击概率的约束下，能够有效平衡联合毁伤概率和平均转火时间，且能够优先使用反应快的火力单元拦截飞临时间短的目标。上述仿真结果验证了本文提出的基于可射击概率约束的WTA模型优点。

3.2.2 优化算法有效性验证

为检验本文提出的基于非线性自适应惯性权重EO算法的性能，分别使用原始EO算法和改进后EO算法进行仿真计算，最大迭代次数为300，种群数量为30，算法随迭代次数的收敛情况如图3所示，算法最优适应度值如表5所示。

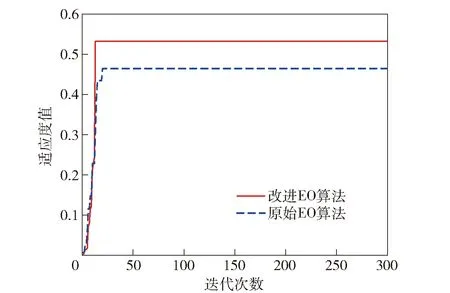
图3 适应度值随迭代次数的变化Fig.3 Change of fitness with iterations

表5 算法的最优适应度值

从图3以及表5中可以看出，改进后EO算法和原始EO算法均能收敛至全局最优解，然而改进后EO算法在收敛速度上和适应度值上都明显优于原始算法，表明非线性自适应惯性权重能够有效平衡算法的局部与全局搜索能力，从而提高算法的寻优效率。

3.2.3 与其他WTA优化算法比较

为进一步验证本文算法的有效性，分别与粒子群优化算法和遗传算法进行对比计算。其中，遗传算法中的杂交概率设置为0.9，变异概率设置为0.04，粒子群优化算法的学习因子设置为2.05，3种算法的最大迭代次数均设置为300，种群数量均设置为30。各算法随迭代次数的收敛情况如图4所示。

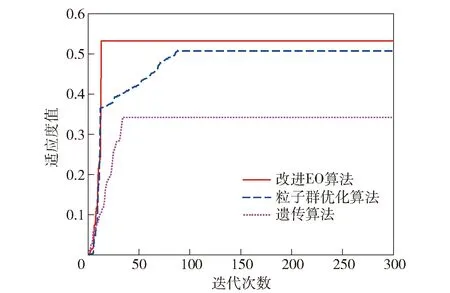
图4 与其他WTA优化算法对比Fig.4 Comparison of the proposed algorithm and other WTA optimization algorithms

从图4中可见：本文所提算法收敛速度最快，遗传算法次之，粒子群优化算法最慢；本文所提算法最优适应度值优于粒子群优化算法，粒子群优化算法优于遗传算法，表明本文所提算法在收敛速度和最优适应度值两方面均优于粒子群优化算法和遗传算法，进一步验证了本文基于非线性自适应惯性权重的EO算法的有效性。

4 结论

本文针对WTA问题建模中未考虑可射击因素的问题，建立一种基于可射击概率约束的防空作战火力优化分配模型；提出了一种基于非线性自适应惯性权重的改进平衡优化器优化算法，对该模型进行求解。通过仿真实验，得到以下结论：

1)在WTA模型中加入可射击概率约束，可在模型中融入影响防空作战的空袭强度、火力单元转火时间等多种因素，使WTA模型更加贴近战场实际。仿真结果表明，该模型能够在保证满足可射击概率和联合毁伤概率阈值的前提下，优先使用反应快的火力单元拦截飞临时间短的目标，并尽量减少火力资源消耗，为防空系统提供持续作战能力。

2)优化算法在初期侧重于全局搜索，在后期则侧重于局部搜索，非线性自适应惯性权重能够引导EO算法更好地平衡局部搜索和全局搜索能力，进而提高寻优能力。