基于压缩感知的多载频随机抖动FMCW信号处理研究

吴宏昊，李 琦，韩壮志，李豪欣，杨晓倩

(1.河北工业大学电子信息工程学院，天津 300000；2.陆军工程大学石家庄校区，石家庄 050000)

0 引言

相对于一般雷达，多载频调频连续波(Frequency Modulation Continuous Wave，FMCW)雷达具有获取目标信息丰富、抗干扰性强、抗噪声性能好、低截获等特点。针对多载频FMCW雷达信号，传统的处理方法是对多载频系统中各通道的回波信号进行距离-多普勒二维FFT处理后合成检测数据[1]。但用二维FFT处理方法对目标进行探测时，会出现多普勒模糊的问题[2]，且直接合成检测数据的方法不能有效利用雷达发射信号的能量，造成能量损失。

压缩感知(Compressed Sensing，CS)[3-4]于2006年被提出，CS理论可以利用信号的稀疏特性，在远小于奈奎斯特采样率的条件下对信号进行重构，因此，可以应用CS理论对多普勒维进行压缩采样，同时结合CS理论的随机性，扩展多普勒无模糊范围。针对多载频信号，文献[5]对每个载波频率均应用MUSIC方法，并利用匹配算法从得到的多个检测数据中提取正确的检测数据；文献[6]提出了一种基于ESPRIT算法的目标识别和雷达散射截面重构方法。这些方法都是应用于均匀采样信号，而对于具有随机性的非均匀采样信号却需要采用协方差插值等复杂的处理过程，因而检测性能和稳定性有所下降。

综上，本文以多载频FMCW雷达为背景，提出一种多载频、调频周期随机抖动的FMCW信号模型及合成处理方法。该方法基于压缩感知理论，将随机性引入多载频FMCW信号；从信号多普勒维的特点出发，采用Keystone变换的方法实现多载频信号合成；采用距离维FFT+多普勒维压缩采样匹配追踪(Compressive Sampling Matching Pursuit，CoSaMP)方法处理合成信号，解决多普勒模糊问题；同时利用互相关补偿相位的方法提升检测精度。经过处理后的多载频、调频间隔随机抖动FMCW信号可以直接进行相参合成，有效扩展了测速范围，同时具有较高的目标检测精度和较好的抗噪声性能。

1 多载频、调频周期随机抖动FMCW信号

1.1 信号模型

文献[7]将随机性引入发射信号波形，提出了一种随机抖动FMCW波形，波形的频率与时间的关系如图1所示，该波形中包含M个调频周期，每个调频周期的调频起始时刻是在均匀间隔的时刻附近随机抖动。其中:f1为发射载频频率；B为发射信号带宽；γ为多普勒维抖动采样因子；Tc为每个调频周期的调频时长；Tar为每个调频周期的重复间隔；ξ为控制随机抖动区间的抖动参量。

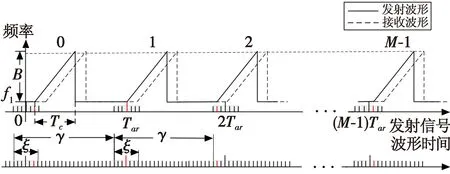
图1 随机抖动波形时频图Fig.1 Time-frequency diagram of random jitter waveform

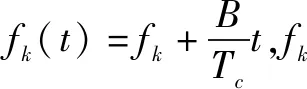
(1)

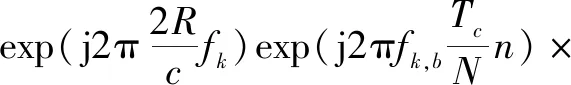
(2)

可以看出，差频频率中既包含目标的速度信息，也包含目标的距离信息，直接通过差频频率求解目标的速度信息就会出现距离速度耦合现象。传统的处理方法是距离-速度二维FFT方法，但该方法存在严重的多普勒模糊问题，需要在多普勒维采用新的处理方法。

1.2 距离维FFT

在多普勒维处理之前，还应先在距离维使用FFT处理，假设每路发射信号发射M个调频周期，对每个调频周期的采样点数为N。首先对M个周期做N点的FFT，得到M×N的二维频谱矩阵，可得第m个调频周期的频域信号为

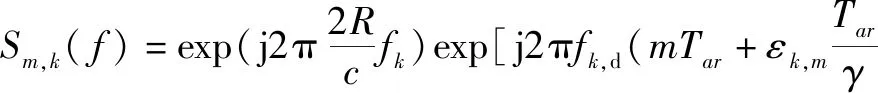
(3)

根据式(3)，在进行距离维FFT处理后，会在f=fk,bTc处出现峰值，它反映了目标所在的距离差频单元，Sm,k(f)在Sm,k(fk,bTc)处取得频谱峰值，它表示目标所在差频单元内的多普勒信号的表达式，即

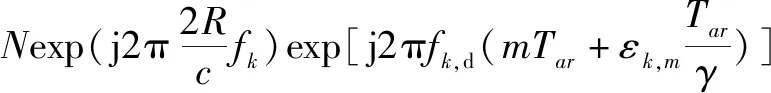
(4)

可以看出，不同载频发射信号的多普勒维信号中fk和εk,m不同，导致相位不同，无法直接合成。

2 多载频、调频周期随机抖动FMCW信号合成处理方法

根据式(4)可知，各路多普勒信号无法直接合成，所以需要一种新的合成处理方法，以其中一路信号为标准信号，将各路多普勒信号不同的载频和不同的抖动随机变量变换为与标准信号相一致。

2.1 Keystone变换信号合成方法

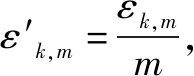
(5)

则第k路信号的多普勒信号可以表示为

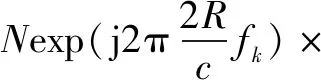
(6)

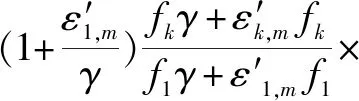
(7)

变换后的信号形式为

(8)

由式(8)可以看出，经过Keystone变换后的各路多普勒信号与标准信号S1,d(m)的多普勒频率变换成了一致的形式，可以直接对多普勒信号合成，假设共有K路不同载频的发射信号，合成后的多普勒信号表达式为

(9)

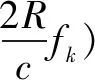
2.2 互相关补偿相位

为使各路多普勒信号的相位完全同步，采用互相关补偿的办法，对经过Keystone变换后的各路多普勒信号与参考的标准信号做互相关处理，对计算出相位差做补偿处理。经过Keystone变换后的各路多普勒信号与参考的标准信号做互相关处理，表达式为

(10)

(11)

经过互相关补偿相位的各路多普勒信号再做多普勒维处理，对目标检测的准确性会明显提升。

2.3 基于CoSaMP算法的多普勒维处理方法

由式(11)可以看出，由于随机抖动变量的存在，需要结合发射信号的随机抖动特性对多普勒信号采用随机抖动采样模式，采样方式如图2所示，其中，f(t)表示频率，t表示时间。

图2 随机抖动采样模式示意图Fig.2 Schematic diagram of random jitter sampling mode

采用CoSaMP算法[8]作为本文方法中的稀疏重构算法，CoSaMP算法采用了回溯的方法，每次迭代选择多个最佳匹配的原子，每次迭代后抛弃一些相关度较低的原子，因此具有较好的稳定特性、易于实现，同时具有较高的重构精度。

2.4 合成处理方法流程及步骤

综上所述，多载频、调频周期随机抖动FMCW信号合成处理方法流程如图3所示。

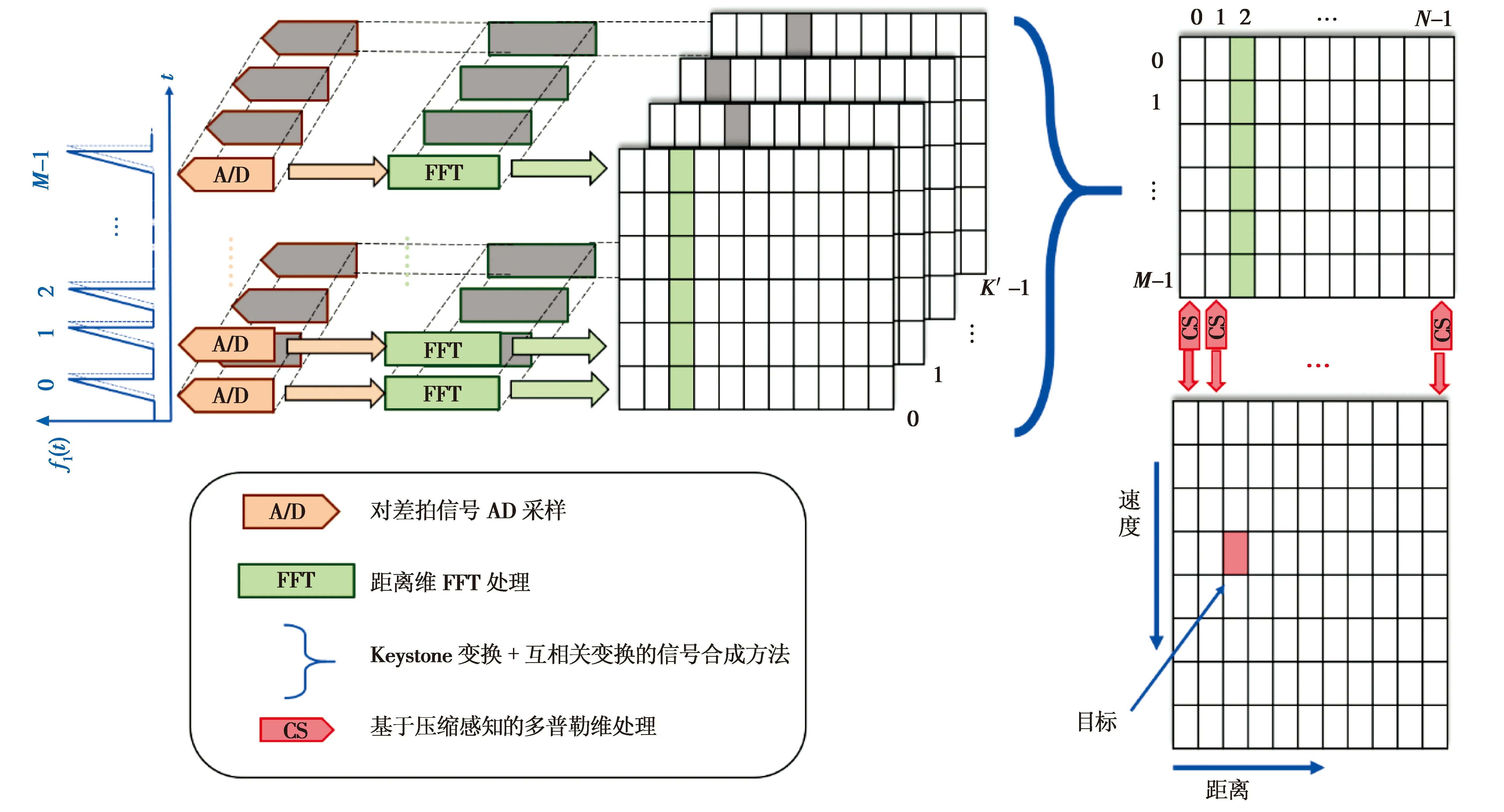
图3 信号处理流程示意图Fig.3 Schematic diagram of signal processing

处理方法具体步骤如下：

1)对接收到的各路回波差拍信号进行A/D采样；

2)对各路差拍信号的距离维做N点FFT，得到K′个M×N的距离二维频谱矩阵；

3)以其中一路信号为参考信号，利用Keystone变换将各路不同载频信号对应的抖动随机变量εk,m和多普勒频率变换为与参考信号一致；

4)对各路Keystone变换后的多普勒信号做互相关处理，进行相位差补偿；

5)直接合成Keystone变换、互相关补偿处理后的各路多普勒信号；

6)采用压缩感知理论，利用参考信号的抖动随机变量生成观测矩阵，利用稀疏重构CoSaMP算法对合成的多普勒维信号进行处理，得到扩展了的多普勒二维频谱；

7)根据所得二维频谱的峰值位置，计算出目标的距离和速度信息。

3 仿真结果与分析

仿真设置了4路不同载频的随机抖动信号，4路载频f1,f2,f3,f4分别为24 GHz，24.5 GHz，25 GHz，25.5 GHz，调频带宽B=250 MHz，调频周期数M=128，每个周期采样点数N=256，平均调频周期Tar=480 μs，每个周期的调频时长Tc=200 μs，多普勒维抖动采样因子γ=16，控制随机抖动的区间的抖动参量ξ=9，4路信号的抖动随机变量ε1,m,ε2,m,ε3,m,ε4,m分别在抖动范围[-4,4]中随机取一组整数。为便于对比效果，假设仅有一个匀速运动目标，初始时刻目标距离雷达42 m，径向速度66 m/s。同时，为了改善频谱泄露的状况，每次距离维FFT处理之前和多普勒维CS处理之前都做了加汉明窗处理。

3.1 最大可测速度范围分析

为验证基于压缩感知理论稀疏重构CoSaMP算法的多普勒维处理方法对解决多普勒模糊、提升最大可测速度范围的有效性，仿真设置了采用传统速度-多普勒二维FFT处理方法处理固定调频间隔Tr=240 μs作为对照，对照实验以第1路f1=24 GHz单载频为例，调频时长均设置为Tc=200 μs，信噪比均为-20 dB，稀疏重构稀疏度为2。

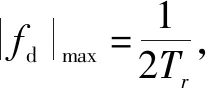
图4所示为传统方法和本文方法的结果对比。

图4 传统方法和本文方法结果对比图Fig.4 Comparison between traditional method and the proposed method

图4(a)采用二维FFT处理方法，二维频谱峰值对应差频频率为260.117 6 kHz，多普勒频率为-2.342 5 kHz，差频频率对应的距离值正确，但多普勒频率对应的速度值错误。图4(b)采用FFT+CoSaMP处理调频周期抖动波形所得差频频率为260.117 6 kHz，多普勒频率为10.196 7 kHz，相应的距离和速度信息均为正确结果。通过对比可以看出，采用FFT+CoSaMP处理的调频周期随机抖动波形有效解决了多普勒模糊问题，扩展了可测速范围。

3.2 信号合成处理方法有效性分析

根据式(9)，经过Keystone变换后的各路多普勒信号的多普勒频率一致，各路回波差拍信号经过距离维FFT处理后可以合成后做CoSaMP处理，结果如图5所示。

仿真在各路信噪比为-20 dB、稀疏度为2的条件下完成，图5(a)所得二维频谱中的一个峰值为正确检测结果，但是各路信号的初始相位项存在差异，导致二维频谱中出现了干扰峰值，从而出现目标检测判决错误；图5(b)是经过互相关补偿相位处理后的结果，二维频谱中仅包含单个峰值，且对应的距离速度信息正确。

图5 Keystone变换、互相关处理结果图Fig.5 Keystone transform and cross-correlation processing result

每次仿真生成的随机抖动变量εm不同，且每次稀疏重构结果有一定的随机性，为进一步分析互相关补偿相位方法的有效性，避免偶然性，仿真实验在各路信噪比为-20 dB下，分别设置稀疏度为1和2两种情况，每种情况做250次蒙特卡罗实验，判断每次目标检测结果是否正确，得到实验仿真结果如表1所示。

表1 互相关补偿处理前后对比结果Table 1 Comparison of results before and after cross-correlation compensation processing

从表1可以看出，当稀疏度为2时，未做互相关补偿处理的准确率明显下降，仅为69.74%，经过互相关补偿处理后准确率可以提升到95.28%左右。实验结果表明，互相关补偿相位处理有效地提升了对目标检测的准确性。

3.3 抗噪声性能分析

为分析本文信号合成处理方法的抗噪声性能，仿真实验了差拍信号分别在-30 dB，-25 dB，…，15 dB，20 dB信噪比下的输出信噪比增益，每个信噪比下做200次蒙特卡罗仿真实验，实验结果如图6所示。

图6 输出信噪比增益示意图Fig.6 Schematic diagram of output signal-to-noise ratio gain

从实验结果可以看出，本文信号合成处理方法可以有效提升输出信噪比增益，尤其在低信噪比的情况下输出信噪比增益明显，在信噪比为-30 dB的情况下可以达到4.95 dB左右的增益，具有较好的抗噪声性能。

4 结论

本文提出一种调频间隔随机抖动的FMCW信号处理方法，该方法采用多载频信号形式，利用Keystone变换在多普勒维合成了不同载频、随机抖动变量的差拍信号，从而改善了信号的抗噪声性能；利用互相关处理补偿相位方法提升了检测准确率；采用压缩感知的思想，利用距离维FFT+多普勒维CoSaMP方法提取目标的距离和速度信息，从而扩展了可测速范围，解决了多普勒模糊问题。本文所提方法可解决多普勒模糊问题，实现多载频信号相参合成，具有较高的检测精度和较好的抗噪声性能，仿真结果验证了本文方法的有效性。