隔离开关与支架体系风振响应

刘 勇，魏珍中，蒋昱楠，杨 萌，周梦瑶，毕文哲

（1.山东电力工程咨询院有限公司，山东 济南 250013；2.山东大学土建与水利学院，山东 济南 250061）

0 引言

受大风天气影响，一些地区特高压换流站直流场部分隔离开关多次出现绝缘支架大幅振动及动静触头闭合困难现象，严重影响变电站的正常运行。截至目前，关于变电站开关设备与支架体系的风振分析以及相应的防范措施研究甚少，相应的规范也未对该领域给出十分明确的理论指导。在已有的研究中，文献[1]采用k-ε 湍流模型和FLUENT软件分析了绝缘子在不同风速工况下的受荷情况，通过对比分析两种近似计算结果，给出了更精确的修正公式。文献[2-4]基于等效静风荷载方法，进行了隔离开关导电闸刀在合闸过程中动触头偏移的分析，由软件计算可知：导电闸刀的应变峰值出现在下部导电杆根部，下部导电杆的应力以及应变水平超出上部导电杆，应通过优化结构设计降低动触头端点的偏移量。文献[5]以zGW6-408 型隔离开关动端结构系统为分析对象开展仿真模拟，用理论公式计算了先导电气组件的变形，并使用ANSYS 软件对隔离开关动端结构系统进行不同风速工况下的变形研究。董新胜等[6]在结构表面脉动风场模拟的基础上，对变电站构架避雷针进行了风振响应时程计算和风振系数分析，并根据分析结果确定了新的风振系数评价指标和新的风振效应评级指标。

这些研究虽对变电站开关设备与支架体系的分析有所帮助，但对隔离开关与支架体系的动力风振响应研究较少，所以开展开关设备与支架体系的整体随机风振响应的数值模拟分析十分重要。本文采用有限元软件开展开关设备与支架结构整体随机风振响应数值模拟分析，并结合开关设备与支架结构风振响应实测数据，对现役开关设备与支架体系提出的加固和减振控制措施，提升开关设备与支架结构设计水平，为开关设备与支架体系的设计提供参考。

1 有限元模型的建立与模态分析

本文以实际工程为背景，选取某ZGW6-408 型高压直流隔离开关，在ANSYS 中分别采用壳单元SHELL181 与实体单元SOLID95 建立了隔离开关及支架体系的动侧开关分闸状态、动侧开关合闸状态和静侧开关的有限元模型，实体单元模型如图1所示。

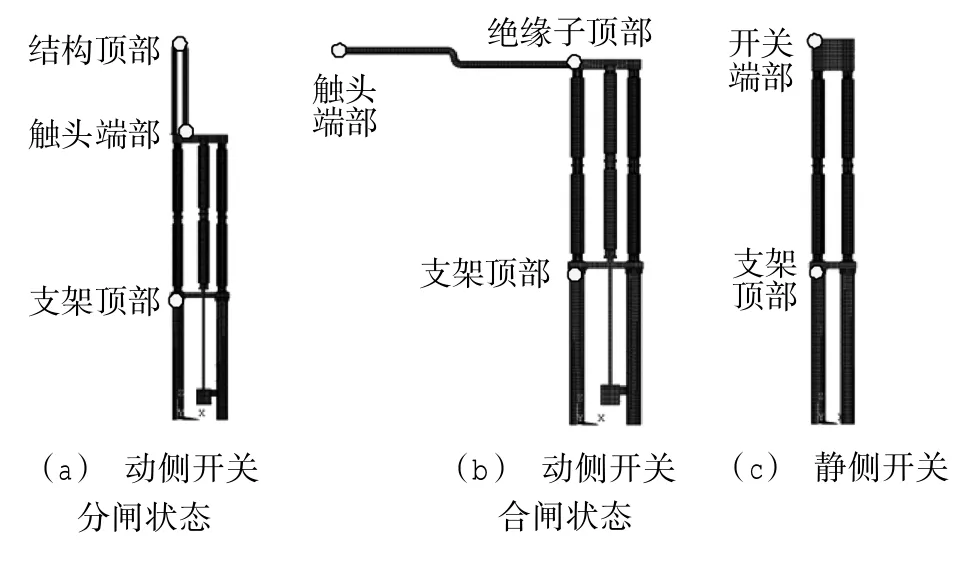
图1 实体单元（SOLID95）有限元模型

由振动系统理论分析可知，较低阶的固有频率和对应的振型对结构的振动起控制作用，较高阶频率所对应的振型在振动控制过程中对结构的振动产生影响比较小，再加上结构阻尼的存在，高频所对应的振型将迅速衰减，真正影响结构动力性能的频率主要为前几阶。因此，在模态分析时，选取隔离开关与支架体系结构的前10 阶模态进行分析，分别求解并提取动侧开关分闸状态、动侧开关即将合闸状态以及静侧开关的固有频率及对应的振型图。

2 开关设备与支架体系体型系数研究

建立包括动侧开关与静侧开关在0°、30°、45°、60°、90°等5 个风攻角下的共10 个流体域模型，计算流域尺寸取140 m×210 m×90 m（宽度×长度×高度）。整个计算流域网格划分为加密区和非加密区两部分，其中开关设备与支架体系附近为网格加密区，加密区体网格的元素主要采用四面体/混合网格；从加密区的5 个表面向外辐射，所辐射到的地方为非加密区。

计算模型的入口边界条件为速度入口，由于隔离开关支架体系高度较低，表面风压受边界层风速变化的影响较小，所以使用均匀流进行计算，取来流平均风速为10 m/s；湍流模型选用SST k-ω 模型，该模型对雷诺数适应性更广，且在工程中得到了广泛应用与验证[7]。出口边界条件为自由出口，其余则采用无滑移的壁面条件。

风荷载体型系数是指风作用在建筑物表面一定面积范围内所引起的平均压力（或吸力）与来流风的速度压的比值，常用式（3）表示。

其中，ωsj为风在建筑物表面引起的实际压力或吸力；ρ 为流体密度，取1.225 kg/m3；ν 为来流速度。

开关设备与支架体系的风荷载体型系数[8]由式（4）计算得到。

表1 给出了隔离开关静侧结构在5 个风向角下体型系数的数值模拟结果与基于规范计算的结果。由表1 可以看出，基于规范计算的下部结构式支架的体型系数明显偏大，其余部位模拟结果与规范较为接近，就结构整体而言，基于规范计算的体型系数相对保守；基于CFD 模拟得到的体型系数90°风攻角下最大，而《变电站建筑结构设计技术规程》[9]中未考虑风攻角的影响，规范中开关与支架体系体型系数的建议取值有待改进。

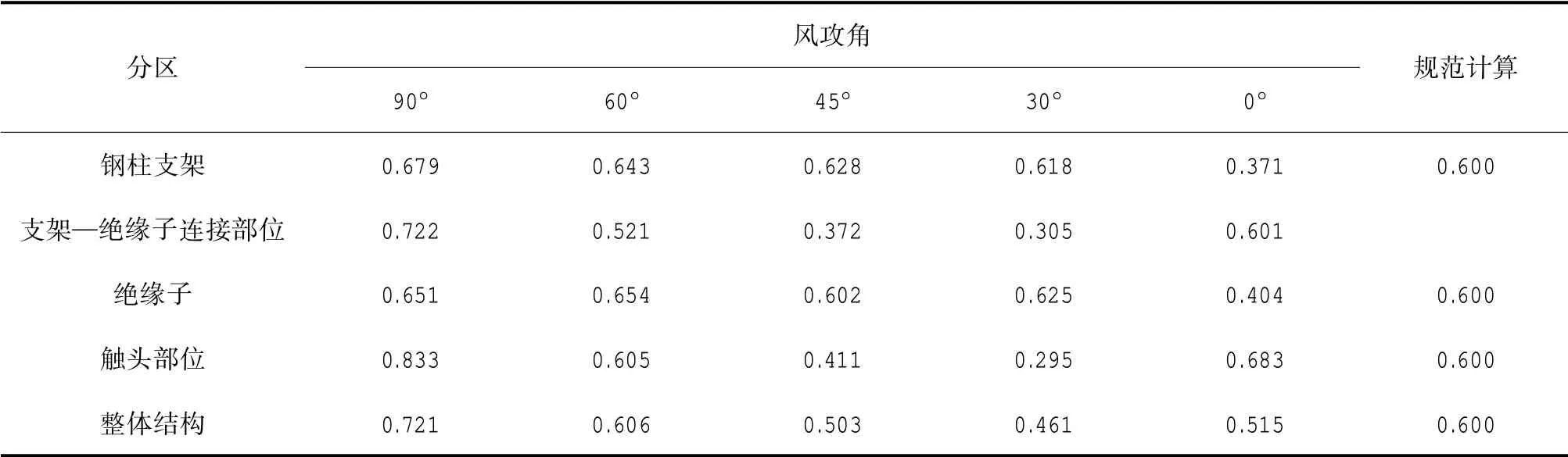
表1 静侧开关结构表面各分区风压体型系数

3 开关设备与支架体系风振响应分析

基于上述所建壳单元与实体单元模型在10 m高度风速为34 m/s 工况下分别开展静力分析，基于设计风速下的隔离开关不同单元类型模型风振响应对比结果如表2 所示，主要包括动侧开关分闸、动侧开关合闸和静侧开关模型。结果表明，采用实体单元和壳单元所建的模型在风荷载作用下结构响应接近，考虑到计算时间成本，故后续基于壳单元开展开关设备与支架体系的风振动力分析。

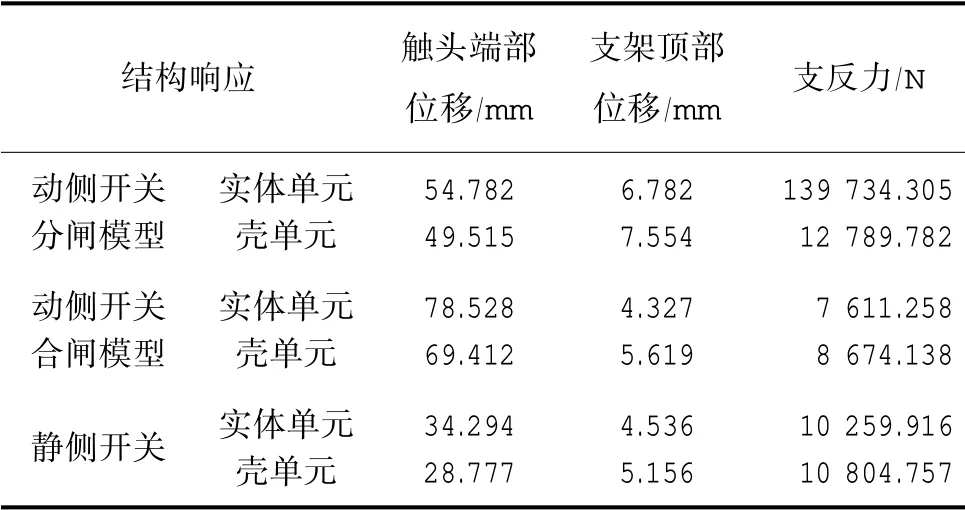
表2 隔离开关不同单元类型模型响应对比

采用Matlab 编制程序，通过基于自回归AR（auto-regressive）模型的线性滤波法模拟隔离开关设备与支架体系结构所受的风压时程，所生成的风压工况共包括动侧开关分闸、动侧开关合闸和静侧开关3 种模型、6 种风速（2 m/s、5 m/s、10 m/s、20 m/s、30 m/s、34 m/s）、5 个角度（0°、30°、45°、60°、90°）共90 个工况。

图2 给出了5 个风攻角下隔离开关与支架体系的支反力响应和支反力矩响应，包括峰值、均方根值和静力计算结果。由此可得：在动侧开关分闸状态时，相同风速工况下均方根值与静力计算结果较为接近，但峰值远大于均方根值和静力结果。在60°风攻角工况下支反力响应和支反力矩响应同时达到最大，此时最大支反力峰值和静力结果分别为36.186 kN 和12.691 kN，支反力矩峰值和静力结果分别为4.752 kN·m 和1.709 kN·m，峰值为静力结果的2.85 倍。虽然支反力矩和支反力的均方根值与静力计算结果具有较好的一致性，但峰值与静力计算结果相差太大，最大差值达23.496 kN 和3.042 kN·m，分别为同等工况下静力计算结果的1.85 倍和1.78 倍。

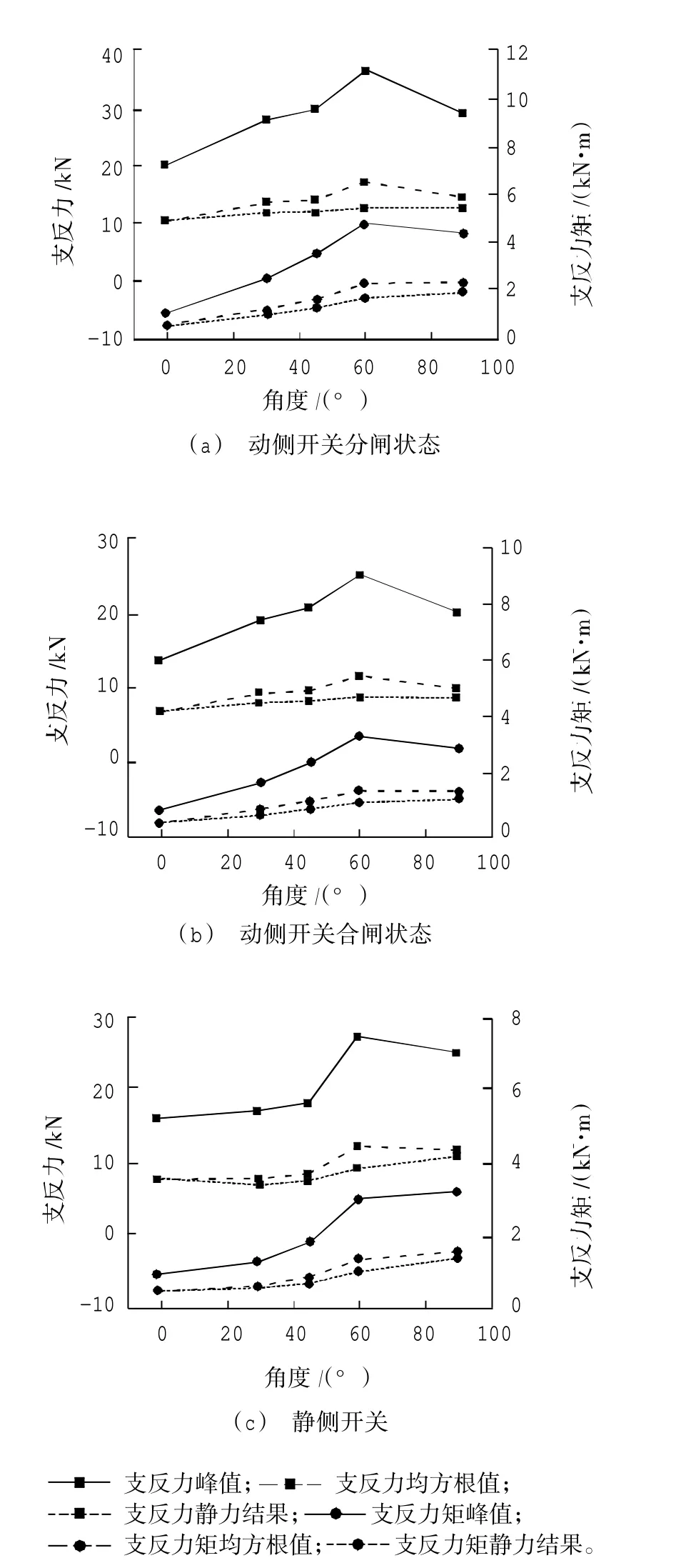
图2 不同风攻角工况下的风振响应

动侧开关分闸状态与合闸状态风振响应变化趋势相同，分闸状态支反力响应和支反力矩响应明显高于合闸状态。静侧开关支反力响应峰值同动侧开关合闸状态峰值响应相近，分别为26.891 kN 和25.354 kN。动侧开关和静侧开关在45°～60°时支反力响应和支反力矩响应变化明显，可认为在此角度范围内，风攻角的变化对结构的风振响应影响较大。相比于支反力响应，支反力矩响应的变化趋势较为平缓。

图3 给出了5 个风速工况下的动侧开关分闸模型支反力和支反力矩响应。对比可得结构响应与风速呈正相关，风速为34 m/s 时支反力响应和支反力矩响应均达到最大值。其中在10～30 m/s 风速区间时，动侧开关分闸状态支反力响应峰值从3.289 kN 升高到26.873 kN，支反力矩峰值响应从0.483 kN·m 提高到4.806 kN·m，响应变化较大，可认为动侧开关分闸状态在此风速区间风振响应较为敏感。均方根值略大于静力计算结果，动侧开关分闸状态时风振响应较大，动侧开关合闸状态与静侧开关在不同风速工况下的风振响应水平相似。

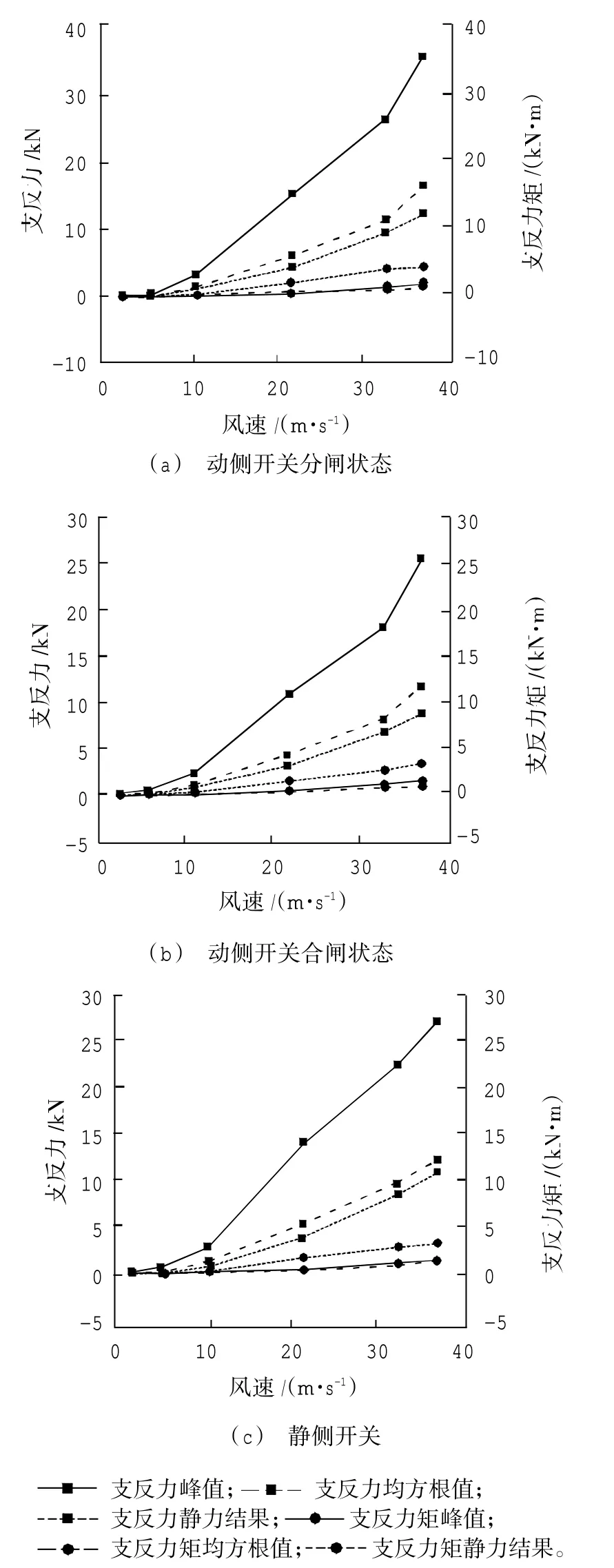
图3 不同风速工况下的风振响应

本小节取10 m 高度处风速为34 m/s，选择5个潜在的不利风攻角（0°，30°，45°，60°和90°），基于MATLAB 模拟的风荷载时程计算该结构的位移风振系数。位移风振系数定义为节点的静动力位移总和与静位移的比值为

其中，β 为风振系数；g 为峰值因子，此处参考《建筑结构荷载规范》GB 50009—2012 取2.5；σsi为位移响应标准差；y 为位移响应均值。

图4 给出了基于动力分析得到的动侧开关合闸状态代表点处的风振系数。《变电站建筑结构设计技术规程》DL/T 5457—2012 中规定，对于设备支架风振系数，500 kV～750 kV 设备支架取1.7；其他设备支架取1.0。通过与时程分析结果对比可知，《建筑结构荷载规范》给出的风振系数建议值明显偏小，动侧开关合闸状态下支架顶部和绝缘子顶部的风振系数计算结果相近，在45°风攻角工况下达到峰值，分别为1.966 和1.973，在0°风攻角工况时触头端部、绝缘子顶部和支架顶部的风振系数小于规范建议值，但在其他工况下都远超规范设计值，这在结构抗风设计中应予以注意。

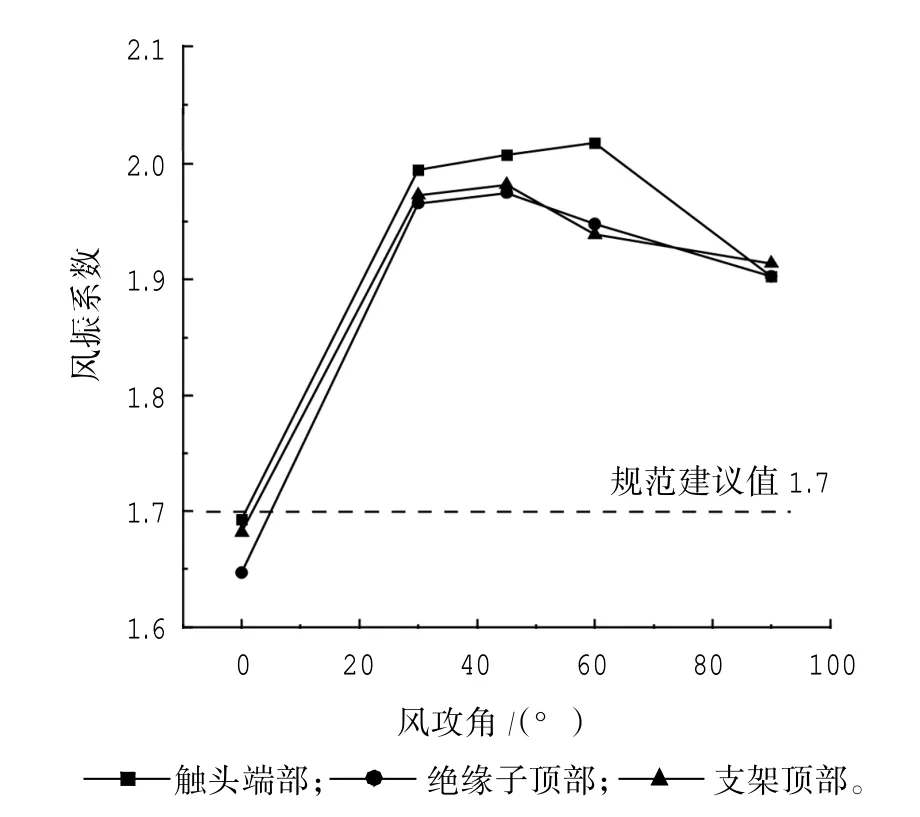
图4 动侧开关合闸状态代表点处风振系数

4 结论

本文通过数值模拟，开展了隔离开关设备与支架体系在风荷载作用下的动力响应分析，研究了其在多种风速风向下的整体风振性能。通过上述研究，得到以下结论。

a）基于实体单元与基于壳单元在风荷载下的结构静力分析结构十分接近，验证了采用壳单元模拟的高效性和正确性。

b）与CFD 模拟结果相比，基于《建筑结构荷载规范》计算的下部格构式支架的体型系数明显偏大，其余部位模拟结果与《建筑结构荷载规范》较为接近。整体而言，基于《建筑结构荷载规范》计算的体型系数相对保守。

c）动侧结构在整个风速时程中的风振响应水平高于静侧结构，开闸状态动触头偏移量较大，对风荷载更敏感；隔离开关与支架体系在60°风攻角下的风振响应最大，0°风攻角下风振响应最小，其位移响应按风攻角0°～60°的顺序呈递增趋势。

d）设备支架在不同风攻角下的风振系数存在明显差异，其中60°风攻角下的风振系数最大，但《建筑结构荷载规范》并未考虑此角度差异。在0°风攻角下模拟所得的风振系数与《建筑结构荷载规范》取值最为接近，而对于斜风向角情况，《建筑结构荷载规范》给出的风振系数建议值明显偏小。

e）设备支架在不同风攻角下的风振系数存在明显差异，其中动侧开关合闸状态触头端部60°风攻角下最大，绝缘子顶部和支架顶部45°风攻角下最大，对于斜风向角情况《建筑结构荷载规范》给出的风振系数建议值偏小。