自适应同步压缩小波变换的风电机组传动链故障诊断方法研究

王振宇，王 平，李永龙

（1.天津科信诚市政工程设计有限公司，天津 300384；2.煤炭工业太原设计研究院集团有限公司，山西 太原 030001；3.青海省绿色发电集团股份有限公司，青海 西宁 810008）

0 引言

风力发电机组由于长期处于野外艰苦环境条件下，其传动链机械部分的振动信号具有变工况、非线性等特点，尤其是齿轮箱部分，其轴承、齿轮箱中的齿轮等部件的振动是造成齿轮箱复杂多分量振动信号的主要成因，其中轴承各零件的频率分布范围较大且不同类型轴承各零件的频率相近，因此，在强噪环境下高精度提取不同轴承各零件的瞬时频率成为学者们近年来的研究热点。

在传统风机的振动监测信号提取处理方法中，傅里叶变换FT（Fourier transform）是最重要的工具之一，但对于非平稳、非线性信号却不适用，其原因是傅里叶变换缺乏时间、频率的定位功能，在非平稳信号分析中有很大的局限性[1]。时频分析技术在一定程度上解决了该问题，但现有的时频分析方法都有一定的局限性。如短时傅里叶变换STFT（short-time Fourier transform）方法[2]，其时间窗的大小、形状都是固定的，与频率无关，无法同时获得精准的时刻和频率，时频聚集性差。魏格纳-威利分布WVD（Wigner-Ville distribution）[3]虽可以获得高的时频分辨率，但在分析多分量信号时存在交叉项。Daubechies 等提出了同步压缩变换SST（synchro squeezing transform）方法，该方法通过对小波变换结果进行重组，利用小波变换后信号频域中相位不受尺度变换影响的特性求取各尺度下对应的频率，再将同一频率下的尺度相加，从而将相同频率附近的值压缩至该频率中，使得时频谱中各频率曲线显现更为清晰和精确。2011 年，Daubechies 等人提出了同步压缩小波变换SWT（synchrosqueezingwavelet transform）。SWT 是一种类似于经验模式分解EMD（empirical mode decomposition）[4]和时频重排RM（reassignment method）[5]的新方法。即在连续小波变换CWT（continuous wavelet transform）的基础上，对变换后的小波系数重新分配，既提高了时频图的能量聚集性，又保留了信号可重建的特性，并达到了消除干扰项、提高振动时频分辨率的目的[6]。结合现有研究结果，本文提出了自适应同步压缩小波变换，解决了传统时频研究方法过程中出现的问题，并利用山西某风电场的风电机组传动链故障数据进行处理验证，结果表明该方法能够很好地提高时频分辨率。

1 瑞利熵

为了能够在内容较为分散的情况下对信号的问题予以全面的体现[7-8]，也能对时频聚集的情况进行全面的衡量，以瑞利熵为基础，建立了识别参数估计算法。信号的熵值越大，时频能量分布结果也会越差[9]。

在分析x（t）信号的过程中，如果假设其中的时频分布函数为TFR（t，ξ）的前提下，另外邻域范围是[t1-τ，t1+τ]的话，那么对应瑞利熵的公式为

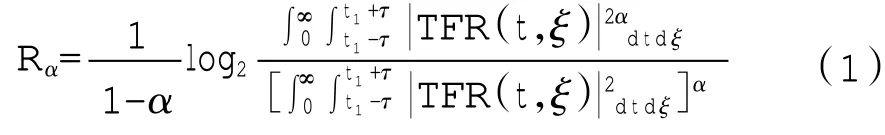
其中，α 为常量，且α>2。

给定一个固定时刻t，可根据式（1）找到一个参数σ，使得TFR（t，ξ）的时频聚集性最好。遍历所有时刻，找到最优的时变参数，具体过程如下。

步骤1：取一系列均匀离散化的尺度参数{σj，j=1，2，…，n}，其中σ1>σ2>…>σn，间隔采样为Δσ=σj-1-σj。信号x（t）离散化，即令t=t1，t2，…，tN。

步骤2：确定一个固定时刻t，计算所有的时变参数{σj，j=1，2，…，n}在时间|t-ξ，t+ξ|范围内的瑞利熵，最终得到{Rσj（t），j=1，2，…，n}。

步骤3：在该固定时刻t 下，在所有时变参数下计算得到的熵值集合中找出最小熵值所对应的σ，则σ 为此刻的最优参数。

步骤4：遍历信号的所有时刻，执行步骤1 与步骤2，找出所有时刻所对应的最小熵值，得到最优参数集合。

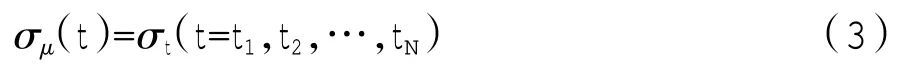
步骤5：用一个低通滤波器B（t）平滑σμ（t），其公式为

σest（t）就是所要估计的时变参数。

2 自适应同步压缩小波变换理论

变换连续小波

傅里叶变换为

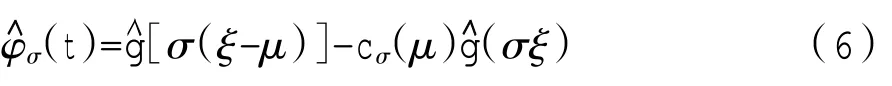
修正小波函数为

在实际情况中，φσ（t）可视为解析小波，表示为

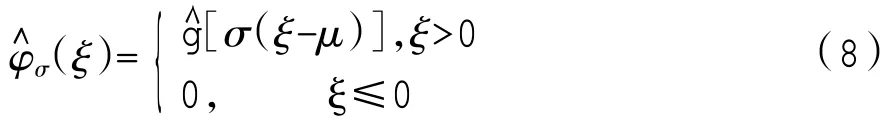
信号x（t）在时变参数下的SST 被定义为

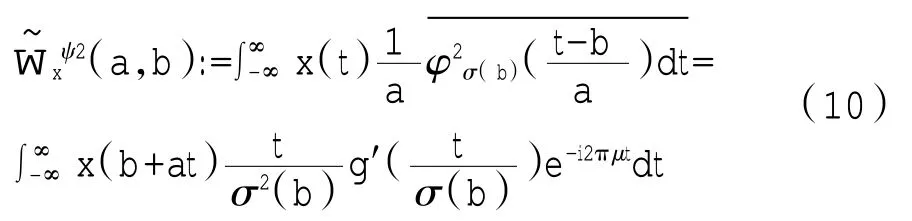
利用单频信号s（t）=Aei2πμt，从

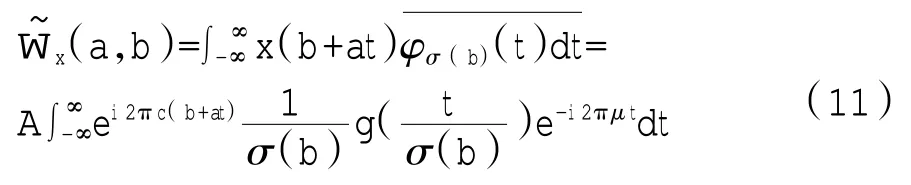
可以得到

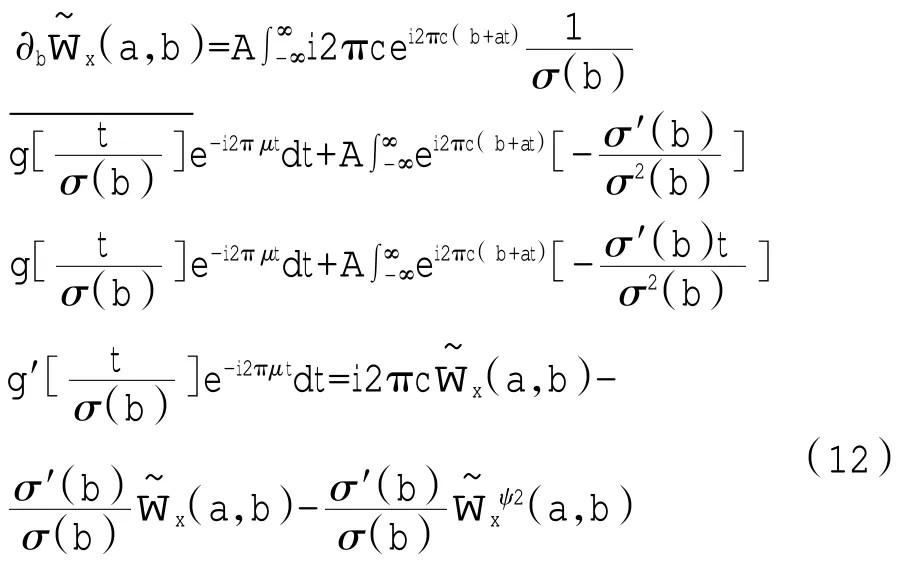
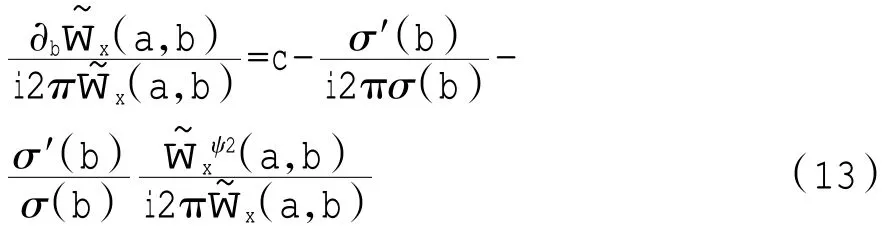
信号s（t）的IF 就是c，可以通过式（14）求得。

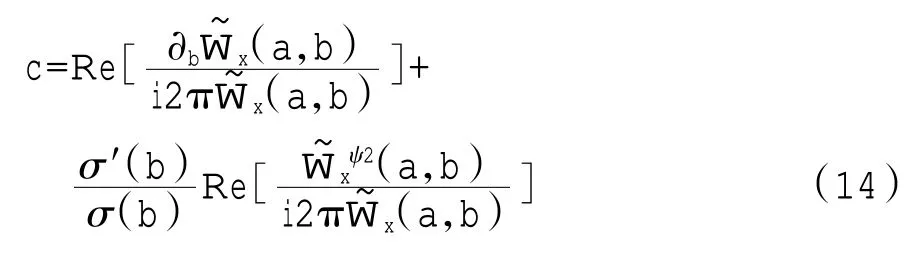
对于一个一般的信号x（t），如果Wx［a，b，σ（b）］≠0，用ωxadp（a，b）表示相位变化：

信号x（t）的自适应SST 被定义为

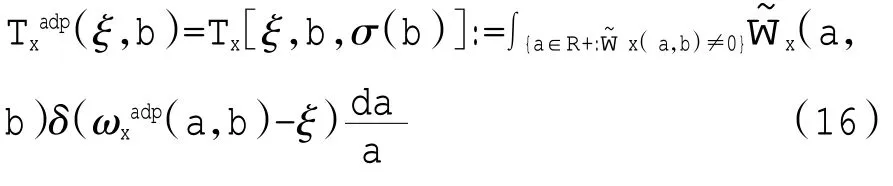
3 分析步骤

小波变换既有频域分析的性质，又能表示发生的时间，有利于分析确定时间发生的现象，有利于各分辨度不同特征的取值。基于自适应同步压缩小波变换阶比分析的研究方法基本步骤如下。

步骤1：输入时域振动信号。

步骤2：获取信号点序列。根据所采集信号的长度，对所采集的信号在大于等于1 的采样频率范围内，选取一个采样频率进行采样，得信号点序列N=Tfs。其中，N 为信号点序列的长度；T 为时间长度；fs为采样频率。

步骤3：选取信号点序列的窗口参数集合。选取morlet 小波；在（0，1）区间，以1/N 的步长，选取N 个不同的值，组成窗口参数集合。

步骤4：计算瑞利熵。在窗口参数集合中，任意选取一个窗口参数，在其对应的窗函数下，对信号点序列进行WSST 变换从而得到对应的WSST 系数；利用瑞利熵公式，计算局部时刻下的瑞利熵值；遍历窗口参数集合中的所有窗口参数，得到局部时刻下对应的瑞利熵值集合。

步骤5：获取最佳窗口参数序列。从瑞利熵值集合中选出最小值，将所选最小值对应的窗函数作为局部时刻下的最优窗函数；遍历每个局部时刻，得到所有局部时刻下的最优窗函数，将所有局部时刻下最优窗函数对应的窗口参数，组成信号点序列的最佳窗口参数序列。

步骤6：获取平滑的最佳窗口参数序列。用滑动平均法，对最佳窗口参数序列内的点进行累加平均，得到平滑的最佳窗口参数序列，并求得对应的窗函数集合。

步骤7：自适应同步压缩小波变换。利用上一步中所求得的窗函数集合进行自适应同步压缩小波变换，并进行瞬时频率的提取。

步骤8：获取阶比谱，利用瞬时频率对信号进行角域采样，得到阶比谱并进行分析。

4 分析过程

4.1 仿真信号分析

本实验设计了变转速信号，基本上与前文所设计的变转速信号相同，都不考虑谐波因素只考虑振动信号的基频。

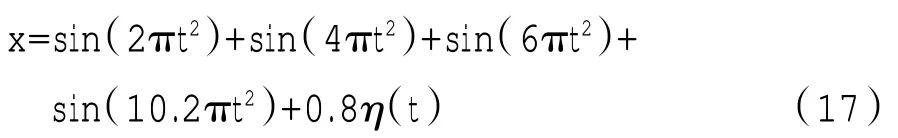
在式（17）中，η（t）代表的是高斯白噪声［η（t）~N（0，1）］，n（t）=2×60t2，nIF（t）=2t2，其中仿真中的参数设置为f=256 Hz，t=8 s。

在其振动信号的时域图中可以明显看出此信号为典型的非平稳信号。

选取Morlet 小波作为小波基进行变化，其参数选择μ=1，尺度变量α 被离散化为σj=2j/nvΔt，nv=32，j=1，2，…，nvlog2N。首先遍历所有时刻，找出最优时变参数集合σest（t），并获取信号的时域图。根据自适应WSST 所得到的时变参数，进行自适应同步压缩变化，获取到小波变化后的脊线区域并成功拟合小波基线，根据小波基线获取信号的瞬时频率，并求得信号的角域采样信号，最终得到信号的阶比谱图。根据所得阶比谱，可以获取数据的阶次信息，与前文所获得的仿真信号阶比谱图相比较，本章介绍的自适应WSST 所获取的角域信号噪声影响小，在阶比谱中可以明显地看出各阶频率无其他毛刺现象。综上所述，自适应WSST 在故障分析中具有极高的准确性。

4.2 实例验证

以山西某风场的F30 号风力发电机组为例，该机组传动系统的发电机前轴承在2020 年5 月发生故障，选取时间节点2020-05-06T8：25：32 时刻的数据进行分析。从图1 所示的阶比谱可以得出振动信号振动冲击明显，并且大部分集中在故障频率的1 倍频、2 倍频以及3 倍频处，呈“枞树形”，与轴承外圈故障情况相同。从此试验可知，本文所提方法可实现对旋转机械故障的诊断。

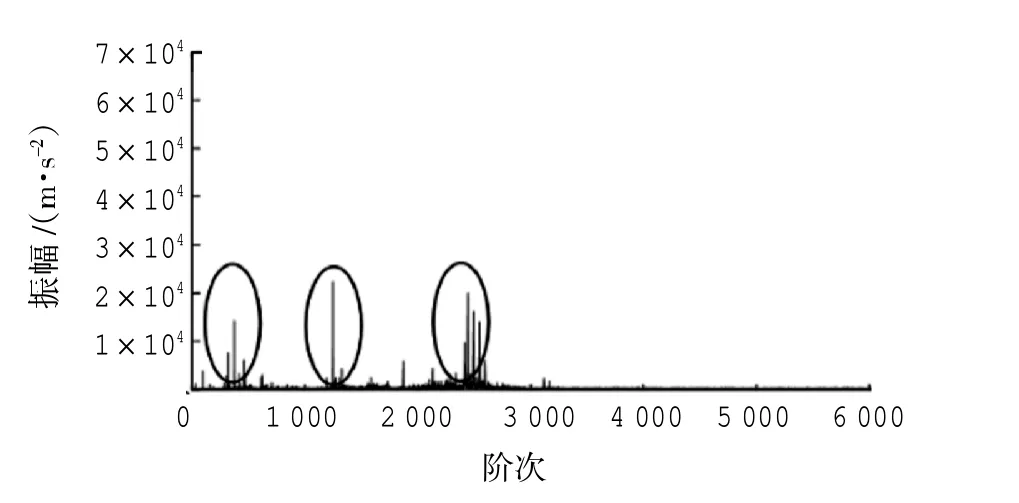
图1 阶比谱图

5 结束语

提出了一种自适应同步压缩小波变换的阶比分析方法，利用仿真数据与实际采集数据做试验，结果表明，提出的改进方法在自适应提取复杂多分量信号的高精度瞬时频率估计等方面具有优越性和实用性。该研究方法为实际生产环境中需要对复杂多分量信号进行分离和提取非平稳信号故障特征的情形奠定了基础，但实际应用及效果仍需在实际情况中加以验证。