长江源区1961～2020年气象要素对水文要素影响的周期性分析

杨颖，李玉雯，马莲，高云鹤，李梦媛，刘增辉，卢素锦*，何奕

(1 青海大学生态环境工程学院，青海 西宁 810016；2 青海大学农牧学院，青海 西宁 810016)

近年来，由自然和人为因素导致的气候变化成为世界各国研究的重点环境问题之一。气候变化导致极端天气频发、生物多样性减少、粮食减产、生态恶化等现象，对人类的生产和生活产生不利影响。国际上对气候变化的研究始于上个世纪70年代后期[1]。国内外学者广泛进行了气候变化对水文水资源影响的研究，得出了气候变化对水文水资源在时空上的重新分配产生了不利影响，水资源脆弱性增加等结论[2]。

水是大气环流和水文循环中的重要因子，径流是流域中气候各种自然地理因素综合作用的产物[2]，是水循环系统中的重要一环。径流过程在整个水资源系统的运行更替中扮演着举足轻重的作用[3]，也是受气候变化影响最直接和最重要的因子之一。水文系统具有时变性，水文时间序列常表现出非平稳特性，小波分析方法能够同时从频域、时域解释时间序列的局部特征[3]，是较为广泛的时间序列分析方法。

采用政府间气候变化专门委员会(IPCC)第五次评估报告提出国际耦合模式比较计划第5阶段(CMIP5)耦合模式及典型浓度路径(RCP)情景，预测RCP2.6、RCP4.5、RCP8.5 3种排放情景下长江源区未来地表径流情况。RCP2.6情景是指把全球平均增温幅度控制在2.0 ℃之内，2100年之前辐射强迫达到最大值，到2100年下降到2.6 W·m-2。RCP4.5情景是指辐射强迫在2100年稳定在4.5 W·m-2。RCP8.5情景是指辐射强迫在2100年上升至8.5 W·m-2。

SWAT(Soil and Water Assessment Tool)是一个长时间尺度的分布式水文模型，适用于具有不同土壤类型以及土地利用的复杂大流域，目前已得到广泛应用[1]。国外将SWAT模型应用于美国德格萨斯州、密西西比河等区域进行径流模拟、分布式水文-土壤-植被模型开发等方面的研究[4-6]；国内先后利用SWAT模型对土地利用、土地覆被变化对径流量的影响等进行研究[7-10]，并对SWAT模型的应用进行了改进[11-12]。SWAT模型可以将流域划分为不同的子流域，并进行多种不同的水运转换的物理过程模拟。

长江源区处于青藏高原腹地，在三江源生态系统中占有重要地位，是气候和生态环境变化的敏感脆弱地区[13]。长江源区生态环境对气候变化的响应得到了国内很多学者的关注。唐建等人通过研究水汽通量揭示了大尺度环流因子对气象水文要素变化的驱动机制[14]；研究表明[15]1961～2010年长江源区气温显著增加，水资源量明显增多。作为青藏高原的重要组成部分，开展长江源区气象水文周期性研究，分析长江源区不同气象要素对水文要素的变化趋势，为应对气候变化的水资源适应性管理策略及防灾减灾策略的提出提供理论依据，对有效分配源区内水资源及水环境保护与恢复具有重要参考价值，对未来长江源区水资源系统的规划设计、开发利用以及水环境保护具有重大的理论和现实意义。

本文利用线性回归、Mann-Kendall突变检验和Morlet小波，对源区气象水文序列的变化趋势及周期进行了分析，初步确定长江源区水文气象要素的演变特征，并运用CMIP5模型中的21种模式的模拟结果，结合RCPs的3种气候情景并耦合SWAT模型，预测未来长江源区地表径流的变化，得到未来长江源区地表径流变化对气候的响应。为长江源区未来气候变化应对策略的提出提供理论依据，对水资源管理、开发利用和社会经济可持续发展具有重要意义。

1 材料与方法

1.1 气象站点的选取

选取青海省境内长江源区的9个气象站点(沱沱河、五道梁、曲麻莱、玉树、安多、杂多、治多、囊谦、清水河)和4个水文站点(沱沱河、楚玛尔、雁石坪、直门达)，收集和观测各站点1961～2020年的平均气温、最高气温、最低气温、降水量和流量数据。各站点经纬度如表1所示。

表1 长江源区气象和水文站点分布情况

1.2 数据来源与测定

1961～2016年的月气温、月降水量数据来自青海省气候中心，1961～2016年的河流月流量数据来自青海省水文水资源勘测局。2017～2020年的日流量、日气温、日降水量数据由实地365天连续监测获得。2017～2020年的实地监测站点与1961～2016年青海省气候中心、青海省水文水资源勘测局的监测站点一致，并将连续监测数据与青海省气候中心、青海省水文水资源勘测局的结果进行比对修正，消除误差，以保证数据的准确性。

气温利用LDX-RM-lx014型干湿温度计和CRM8-XH-202型最高、最低温度计测量，温度计安装在百叶箱中，可在自动记录纸上得到任何时刻的温度；降水量采用15184型称重式雨量计测量；河流流量采用25-1型流速仪结合半自动缆道施测，由室内人工控制采集和传输流量。

1.3 CMIP5模型与SWAT模型的耦合

将CMIP5气候模型中21种模式的模拟结果，经过插值计算将其统一降尺度到同一分辨率下，利用简单平均方法进行多模式集合，制作成一套包括1901～2005年Historical和2006～2100年RCP2.6、RCP4.5、RCP8.5排放情景下的月平均资料，这21种模式包括Beijing Climate Center Climate System Model version 1，Beijing Normal University Earth System Model，Canadian Earth System Model version 2，Flexible Global Ocean- Atmosphere-Land System Model-grid version 2等，21种模式对气温和降水的模拟效果较好。

构建了长江源区的SWAT模型，通过高程数据对长江源区进行分带设置，并分析沱沱河、楚玛尔、雁石坪、直门达这四个水文站的水文数据，在经过处理的四个水文站点的DEM图中提取河网，选取直门达水文站作为长江源区的流域总出口，在模型中输入直门达水文站的经纬度坐标，然后划分出长江源区子流域。将长江源区划分为31个子流域，202个水文响应单元(HRU)。1961～2016年为模型的模拟时间，其中模型的预热期为1961～1965年，2017～2020年进行模型的验证。验证期相对误差为3.34%，决定系数为0.89，系数率定期相对误差为5.27%，决定为0.84，表明在率定期内的实测值与模拟值拟合较好，SWAT水文模型对长江源区净流量的模拟符合实际，表明SWAT水文模型适用于长江源区。

利用CMIP5气候模型中21种模式的模拟结果，选取模式中3种典型温室气体浓度的排放路径(RCP2.6、RCP2.6、RCP8.5)，将气象因子模拟预估序列数据输入到已率定好的SWAT模型[15]，完成SWAT降尺度模型与CMIP5模式下的RCPs情景输出序列的耦合，得到未来(2022～2100年)长江源区地表径流对气候变化的响应。

1.4 分析方法

1.4.1 Mann-Kendall突变检验及线性回归及方法

采用线性回归方法[16]、Mann-Kendall突变检验[17]对气温、降水量、河流流量的变化趋势进行分析。

1.4.2 小波分析

采用Morlet小波[17]对研究区域气象水文序列的周期性变化进行分析。

1.5 数据处理

采用Origin 8.0软件对数据进行整理并进行线性回归分析，小波分析过程在软件MatlabR 2018a命令窗口中实现，采用Surfer 8软件制作小波变换图。

2 结果与分析

2.1 长江源区气象要素对水文要素趋势变化的特征

采用线性回归方法和MATLAB软件，对气象水文要素进行Mann-Kendall趋势检验和突变点检验及变化趋势分析。

60年间长江源区的年平均气温呈现升高趋势，而且趋势显著(P<0.05)，年际增温变化率约为0.39 ℃/10a，增温率高于最高气温和最低气温。2020年长江源区年平均气温为1.42 ℃，比60年平均气温(-0.89 ℃)高出2.31 ℃，是21世纪的最高值。1965年的平均气温是60年间的最低值，为-2.32 ℃。

平均气温趋势检验值Z=6.76，其大于2.32，表示置信度通过了99%的显著性，说明长江源区流域年平均气温在60年的长时间序列数据上呈现上升趋势，并且上升趋势十分显著。整个时间序列中UF值的大小有较大波动。大体来看，1988年之前，UF值基本都小于0，则表明此段时间年平均气温序列有下降趋势。1988年至2020年，UF值全部大于0，则表明这段时间年平均气温呈现上升趋势，且2000年之后，UF值超过临界值，反映从新世纪开始，长江源区流域年平均气温上升趋势十分显著。UF曲线和UB曲线在α<0.05置信水平上，两者未出现交点，交点位于临界线范围外，所以该年份参数突变性上升不具有突变性，交点大致为2005年。结合前面的关于年平均气温均值曲线、年平均气温滑动平均曲线的研究，与M-K检验结果完全一致(图1)。

图1 年平均气温变化趋势图及M-K统计量曲线

2.1.2 年最高气温变化特征

年最高气温呈现升高趋势，而且趋势显著(P<0.05)。60年平均值为13.40 ℃。年际增温率约为0.37 ℃/10a。年最高气温最高的年份是2020年，为16.30 ℃，比多年平均值高出3.00 ℃。最低的年份是1997年，为11.63 ℃。

最高气温趋势检验值Z=5.44，其大于2.32，表示置信度通过了99%的显著性，说明长江源区流域最高气温60年的长时间序列数据上呈现上升趋势，并且上升趋势十分显著。整个时间序列中UF值的大小有较大波动。大体来看，1963年至1982年、1988年至2020年UF值都大于0，最高气温呈现上升趋势；1983年至1987年UF值小于0，呈现下降趋势。UF曲线和UB曲线在α<0.05置信水平上，两者出现交点，且交点位于临界线范围内，则表明长江源区最高气温在长时间序列1960至2020年上存在突变时刻，突变点大致为2005年。可见进入新世纪年最高气温偏高，与线性回归分析一致(图2)。

通过上述分析，吉奇对弗雷格判断杠的不当使用就很清楚了。弗雷格的判断杠是加在被他称为“语句”的单独词项之前的。因为这样的“语句”本身不具备判断力，而无法被用来做判断，所以当我们想做判断时，就需要通过判断杠将它改造成具有判断力的表达式。弗雷格引入判断杠“|”是必要的，他需要这样一个符号来将已被他剥夺了判断力的语句再恢复判断力。吉奇在没有明确弗雷格本意的前提下就直接借用判断杠“|”，并加在自然语句之前，是错误的。因为自然语句不是单独词项，它本身就携带判断力，没有必要再为它加上判断杠。

图2 年最高气温变化趋势图及M-K统计量曲线

2.1.3 年最低气温变化特征

最低气温呈现显著的上升趋势(P<0.05)，60年的平均最低气温为-13.99 ℃，年际变化率约为0.54 ℃/10 a。年最低气温值出现在1965年为-15.67 ℃，比多年平均值低1.68 ℃。最高的年份是2009年，为-12.04 ℃。由10年平均滑动的曲线可见，60、70、80、90年代，年平均气温低于平均值，进入21世纪以来，气温大幅度上升；年最高气温普遍偏低，21世纪以来，年最高气温偏高；年最低气温普遍偏低，本世纪以来，年最低气温高于平均值。

最低气温趋势检验值Z=5.78，其大于2.32，表示置信度通过了99%的显著性，说明长江源区流域最低气温60年的长时间序列数据上呈现上升趋势，并且上升趋势十分显著，1960年至1993年UF值小于0，最低气温呈现下降趋势；1994年至2020年UF值大于0，呈现上升趋势。UF曲线和UB曲线在α<0.05置信水平上，两者出现交点，且交点位于临界线范围内，则表明长江源区最低气温在长时间序列1960～2020年上存在突变时刻，突变点大致为2000年。可见进入新世纪年最低气温偏高，呈现上升趋势，与线性回归分析一致(图3)。

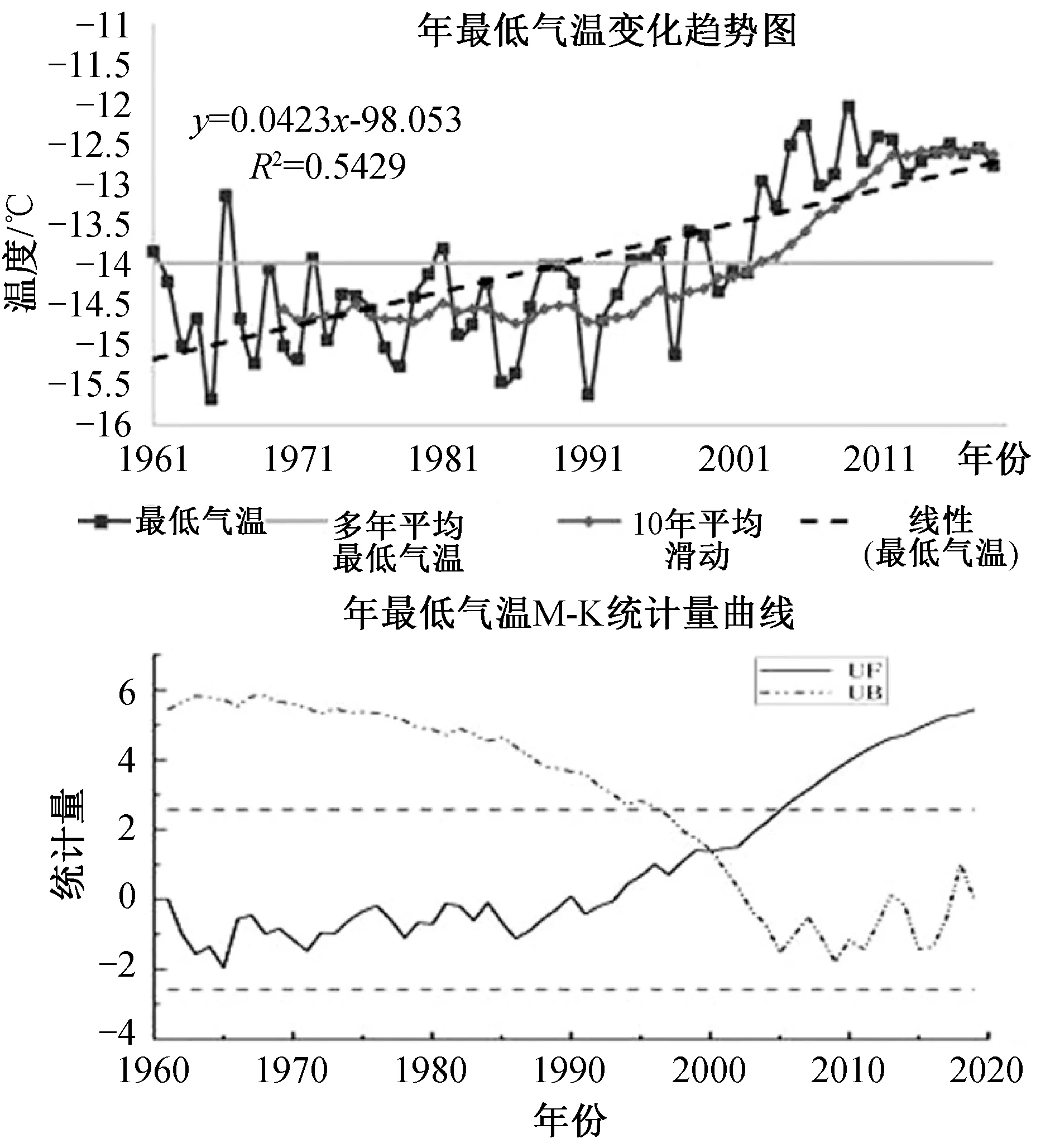
图3 年最低高气温变化趋势图及M-K统计量曲线

2.1.4 年降水量变化特征

60年间长江源区的年降水量呈现增加趋势，但趋势不显著(P>0.05)。源区年降水量为28.72 mm～44.68 mm，最低年降水量出现在1984年，最高年降水量出现在1989年，年际降水变化率约0.24 mm/10a。10年平均滑动的曲线显示，60、70、80、90年代在平均值附近波动，降水量偏少，21世纪以来，降水量有所增多。年降水量趋势检验值Z=0.78，置信度小于90%，年降水量增长趋势不显著。1966年至1990年、2001至2006年UF值小于0，年降水量呈现下降趋势；1991年至2000年年降水量呈现波动上升趋势，2006年之后呈现明显上升趋势。UF曲线和UB曲线在α<0.05置信水平上，UF和UB交点分别出现在1983年、1988年、1992年、1997年和2015年，且交点位于临界值内，说明长江源区年降水量分别1983年、1988年、1992年、1997年和2015年发生突变。M-K检验和年最低气温变化趋势结果一致，21世纪以来，降水量有所增多(图4)。

图4 年降水量变化趋势图及M-K统计量曲线

2.1.5 年流量变化特征

60年间长江源区年流量呈现增加趋势，但趋势不显著(P>0.05)。年际流量变化率约为8.6 m3/(s·10a)，变化率小。60到90年代，自1989年达到最大值后，一直处于偏枯状态。21世纪以来流量高峰出现在2012年。从10年平均滑动的曲线可以看出，上个世纪60～90年代的流量都低于60年平均值，但90年代流量相对偏低，21世纪有所增加。

年流量趋势检验值Z=-0.33，置信度小于90%，年平均流量增长趋势不显著。1960年至1967年UF值大于0，长江源区年平均呈现上升趋势；1968年至2020年UF值小于0，年平均流量呈现下降趋势。UF曲线和UB曲线在α<0.05置信水平上，UF和UB交点分别出现在1966年、2005年、2007年和2012年，且交点位于临界值内，说明长江源区年流量分别在1966年、2005年、2008年和2012年发生突变。M-K检验的结果和年降水量变化趋势分析结果一致，长江源区年平均流量在21世纪有所增加(图5)。

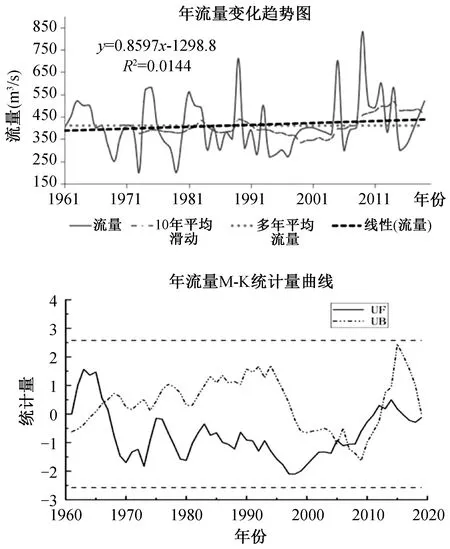
图5 年流量变化趋势图及M-K统计量曲线

2.2 长江源区气象要素对水文要素周期性变化特征

运用Morlet小波分析方法对长江源区气象水文要素进行周期分析。

1961～2020年长江源区年平均气温存在20～25年、8～11年和3～5年的周期。20～25年的周期振荡，长江源区的年平均气温经历了8个时期的冷暖交替变化，强度较强，包括4个明显气温变冷时段和4个明显气温增暖时段，等值曲线未闭合，未来几年处于增温期；8～11年的周期振荡长江源区的年平均气温经历了14个时期的冷暖交替变化，包括7个增暖期和7个变冷期，2006年之后比较稳定。

年平均气温小波方差分析显示(图6A)，年平均气温存在22年、10年、4年的周期，其中，最大峰值对应着22年周期的振荡，第二峰对应着4年周期，第三峰值对应着10年周期的振荡，其中4周年、10周年振荡相差较小。说明22年的周期是这一时域的主周期。图6A中正值表示气温偏暖，负值表示气温偏冷。

源区年最高气温存在24～29年、14～16年的周期两类时间尺度变化规律，这两个时间尺度的周期变化在这个研究时域中具有全域性的特点。24～29年、14～16年的周期振荡，源区的年最高气温分别经历了8个时期的交替变化，包括4个变暖期和4个变冷期，2016年以后等值曲线未闭合，呈变暖趋势。最高气温小波方差分析表明(图6B)，年最高气温存在27～29年、18～20年的周期，其中，最大峰值对应着27～29年周期振荡，第二峰对应着18～20年周期振荡。年最高气温一直处于上升趋势，这说明最高温度时间序列会有一个更大的周期振荡。图6B中正值表示气温升高，负值表示气温降低。

源区年最低气温存在30～32年的周期，这个周期变化在这个研究时域中具有全域性的特点。30～32年的周期振荡，源区的年最高气温经历了7个时期的交替变化，包括3个变暖期和4个变冷期，2016年以后呈现变冷趋势。年最低气温小波方差分析表明(图6C)，最低温度时间序列呈上升趋势，未来可能会有一个更大的周期振荡。图6C中正值表示气温升高，负值表示气温降低。

1961～2020年，长江源区年降水量存在18～30年，9～17年的周期，3～8年的周期。这3个周期变化在这个研究时域中具有全域性的特点。18～30年的周期振荡，源区的年降水经历了7个时期的交替变化，包括3个增加期和4个减少期。2011年以后减少趋势；9～17年的周期振荡，源区的年降水量经历了13个时期的交替变化，包括7个增加期和6个减少期。3～8年的周期振荡，源区的年降水量21个时期的交替变化，包括11个增加期和10个减少期。年降水量小波方差分析显示(图6D)，年降水存在27年、14年、7年、3年的周期，其中，最大峰值对应着27年周期振荡，第二峰对应着14年周期振荡，第三、四峰值分别对应着7年、3年的周期振荡。其中27年是这一时域的主周期。图6D中正值表示降水增多，负值表示降水减少。

源区年流量存在27～32年，10～17年的周期，3～8年的周期。27～32年的周期振荡，源区的年流量经历了5个时期的交替变化，包括2个偏丰期和3个偏枯期。10～17年的周期振荡，源区的年流量经历了13个时期的交替变化，包括7个偏丰期和6个偏枯期。3～8年的周期震荡小，可知源区的年流量振荡不大。年流量小波方差分析确定(图6E)，年流量时间序列存在27～30年、13年、9年、7年、3年的周期，其中27～30年的周期为这一阶段的主周期，此后方差曲线一直处于上升趋势，流量时间序列应遵循一个更大的周期变化。图6E中正值表示流量偏丰，负值表示流量偏枯。

27周期的流量小波系数和降水量小波系数有较强的相关性，并通过了95%的显著性检验。推测出年流量27年的周期主要是由降水所导致(图7)。

图6 1961～2020年长江源区不同气象要素小波变换图

图7 长江源区27年周期的流量和降水量的小波变换系数相关性图

2.3 未来气候情景下长江源区地表径流的变化分析

在CMIP5模型的3种情景下，地表径流的年际变化很大，总体呈现出下降趋势，在RCP2.6气候模式下，2048年径流量是最大的；在RCP4.5气候模式下，2035年径流量是最大的；在RCP8.5气候模式下，在2036年径流量是最大的(图8)。

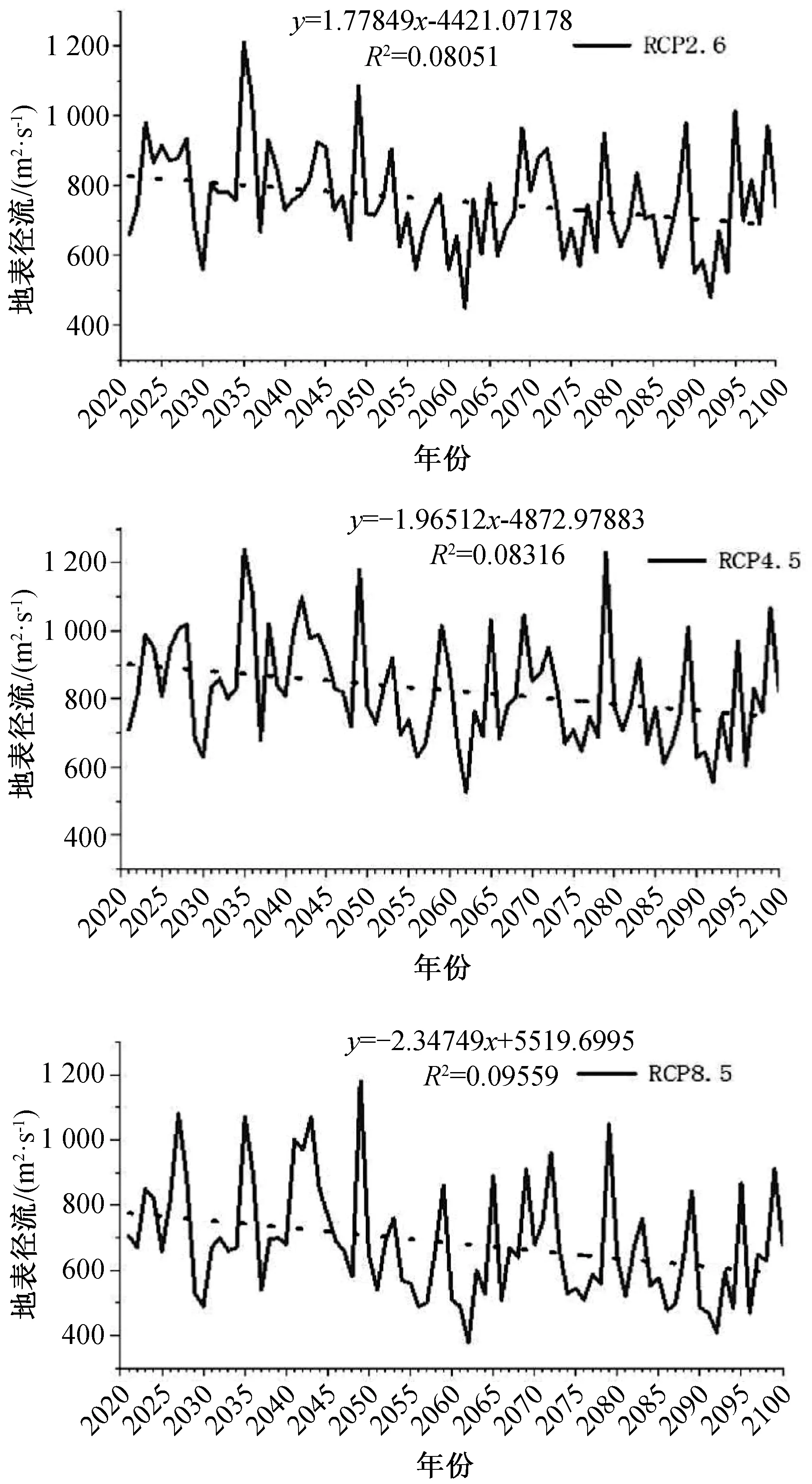
图8 3种气候情景下地表径流的年际变化图

3 讨论与结论

本研究中雁石坪、楚玛尔、沱沱河、直门达水文站1961～2020年平均流量与年降水量呈增加趋势，但增加不显著，2005年流量与年降水明显增加，这与朱延龙[18]、齐冬梅[19]等人得出的结果一致，主要是因为气温急剧升高，降水增多，冰川、积雪融化所致[18-20]。前人有关长江源区气象水文要素变化研究主要集中在2016年以前，本文的研究增加了源区气象水文要素研究的时间序列；长江源区60年(1960～2020)气温、降水量和流量存在周期变化，主要周期出现7个左右的交替，气象水文变化呈现多周期性、振荡性的特点，且不同要素在不同周期历经多次变化，这与朱海涛[20]、张代青等[21]的结果相一致；年平均气温的主要周期的等值线未完全闭合，年气温将继续升高，与刘光生等[22]研究结果一致；年流量和年降水量都存在27年周期且相关性强。这与齐冬梅等[19]的研究结果一致；长江源区年平均气温、年降水量和年流量周期与朱海涛[20]、刘光生[22]、杨建平等[23]气象水文序列周期也存在差异，分析其原因，气象水文序列的周期变化除受气候变化影响外，还受天体运动变化如太阳黑子活动以及下垫面因素的影响有关。太阳黑子活动主要影响气象序列[23]，而对于下垫面因素(地理位置、海拔高度等)，由于不同时间尺度和不同研究对象，对下垫面条件的依赖程度也不同。下垫面对某一地区气温和降水量的周期变化影响不大，但对水文序列的周期变化影响较大。气候变化和太阳活动会直接影响气温和降水量的周期变化，进而在一定的下垫面因素下，流量的周期变化也会受到影响[24]。有关天体运动变化和下垫面因素对气象水文序列周期变化的影响将有待于进一步深入研究。

本研究中，未来情景模式下，地表径流年际变化呈下降趋势，径流变化随气温和降水量变化而变化，且在2034年和2048年达到最大值，不确定性较大，与程志刚[25]研究结果一致，但与俞烜[26]研究结果不同，地表径流呈缓慢增加趋势，其主要原因是源区降雨量增加，气温的升高增加了冰川融水对地表径流的补给，从而导致未来预测结果的不同[26]。

王锦旗等[27]利用SWAT模型对黄河源区1988～2005年的地表径流进行模拟得出，在个别年虽有一定的误差，但模拟结果与实测结果基本相一致，具有参考价值；李硕[28]在遥感和GIS的支持下，对SWAT模型的空间参数化和离散化进行了研究，并成功的将SWAT模型运用到径流模拟研究中；张永勇等[29]利用CN2、ESCO、SOL等主要参数和SWAT模型预测未来2010～2039年长江源区的径流演变趋势，表明未来三十年源区总体径流量呈现减少趋势，但在洵期径流量增大。本研究中，运用CMIP5模型中的21种模式的模拟结果，结合RCPs的三种气候情景并耦合SWAT模型下，预测未来长江源区地表径流的变化，取得了较好效果。已有研究表明，相比单个模式，模式集合平均模拟效果往往更好。

本文对1961～2020年长江源区年平均气温、年最高气温、年最低气温、年降水量和年流量进行了趋势分析、Mann-Kendall突变检验和Morlet小波周期分析，运用CMIP5模型中的21种模式的模拟结果，结合RCPs的3种气候情景并耦合SWAT模型，得出以下结论：

(1)年平均气温、年最高气温、年最低气温均显著上升，年降水量和年流量呈现增加趋势，但趋势不显著。(2)年平均气温存在22年、10年和4年周期，未来几年长江源区将处于增温阶段；年最高气温存在27～29年和18～20年的周期，未来可能会有一个更大的周期震荡；年最低气温在未来可能会有一个更大的周期震荡。(3)年降水量存在27年、14年、7年和3年的周期。年流量存在27～30年、13年、9年、7年、3年的周期，之后在时间尺度上还应遵循一个更大的周期变化。(4)年流量和年降水量都存在27年周期，其相关性较强，年降水量与径流量量突变特征基本一致，表明这一时期年径流量突变主要由降水量变化引起。(5)未来情景模式下，地表径流量年际间变化较大，不同情景趋势下，不稳定性较强，总体的年际径流量都为下降的趋势，下降幅度最大的是RCP8.5，最小的是RCP2.6。加强长江源区气候变化应对策略迫在眉睫。

4 展望

气候变化对水文影响作为一个较新的研究方向，研究成果尚不够系统深入。本文对长江源区1961～2020年气象要素对地表径流的影响进行了周期性分析，受长江源区近些年蒸发量研究数据较少、不全面的影响，本文未考虑气象要素对蒸发的影响。但蒸发量是水循环中最易受土地利用和气候变化影响的因素之一，后续将进一步开展蒸发量对水文循环过程中的影响研究。

定量分析和区分气候变化和人类活动相结合对长江源区水循环及水资源的影响。气候变化是影响源区水文过程的主要因素，而人类活动对源区水文水资源也存在较大的影响。本文由于时间有限并未考虑人为影响。在后续的工作中，可开展气候变化和人类活动共同对水文循环的影响，定量分析长江源区对水文水资源的影响。