变时滞反馈控制的混合中立型随机延迟微分方程的稳定性

周之薇，宋瑞丽

变时滞反馈控制的混合中立型随机延迟微分方程的稳定性

*周之薇，宋瑞丽

（南京财经大学应用数学学院，江苏，南京 210023）

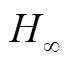
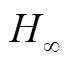
0 引言

随机微分方程（SDDE）描述了随机系统不仅依赖于现在的状态，同时也依赖于过去的状态。许多科研人员研究了随机微分方程的稳定性和有界性[1-4]。而连续时间的马氏链是用于描述随机系统突然性的结构变化。Mao在文献[5]中研究了带有马氏链的随机微分方程，这样的随机系统又被称之为混合的随机延迟微分方程。混合随机延迟微分方程的有界性和稳定性可以参考文献[6-14]。而混合中立型随机延迟微分方程（NSDDEs）是用来描述一类混合随机微分方程依赖于过去一段时间状态的变化率。混合中立型随机延迟微分方程的稳定性相关研究可以参阅文献[15-19]。

但是，有一些随机系统是不稳定的。最经典的做法是在不稳定的随机系统中加入反馈控制函数，从而使随机系统变得稳定。文献[20-25]研究不稳定随机系统稳定化的问题。文献[20]研究了延迟反馈控制的混合中立型随机延迟微分方程的稳定性问题，其中漂移系数和扩散系数满足线性增长条件。文献[24]研究了延迟反馈控制的混合中立型随机延迟微分方程在多项式增长条件下的稳定化问题。以上文献所提及的时滞都是常数。而变时滞的随机系统并不拘泥于一个常数，可以推广到函数，这将会带来更多的实用价值，所以有必要去研究在变时滞反馈控制且具有变时滞的混合中立型随机延迟微分方程在多项式增长条件下的稳定化问题。

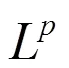
1 模型描述和假设

考虑以下NSDDE，

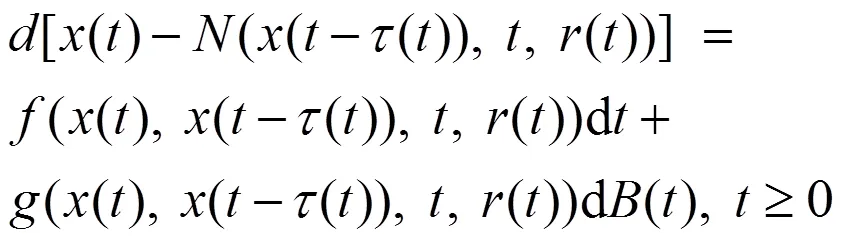
初值：

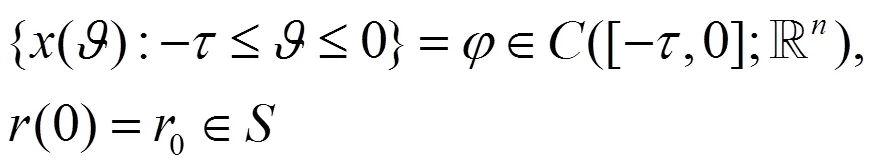
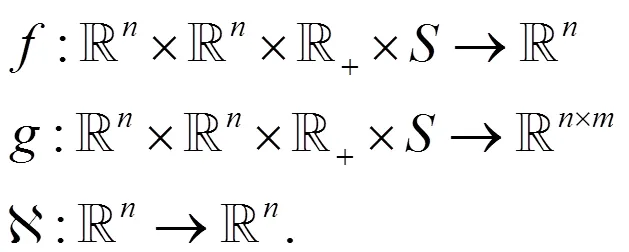
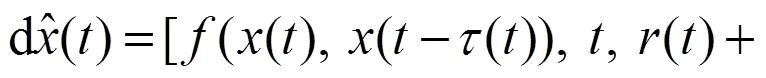
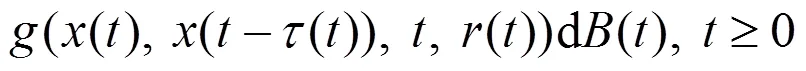
基于稳定性问题的研究，

假设

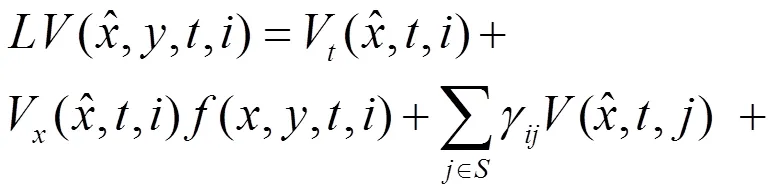
提出以下假设:

假设1（局部李普希兹条件）

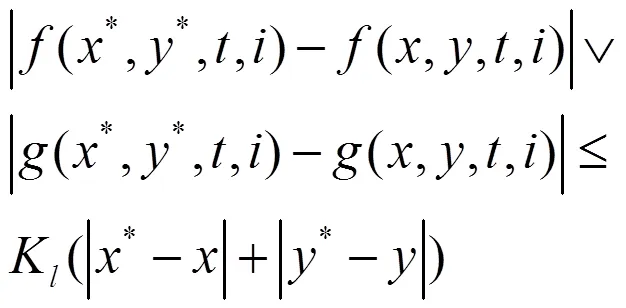
假设2（多项式增长条件）

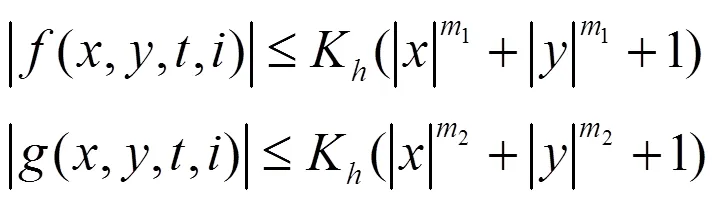
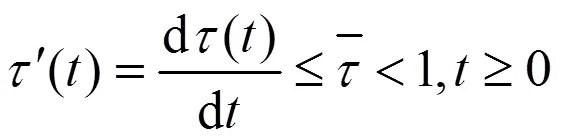
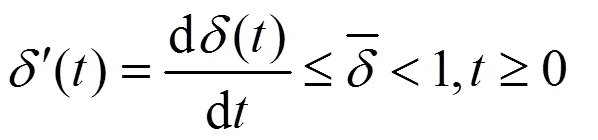
(9)

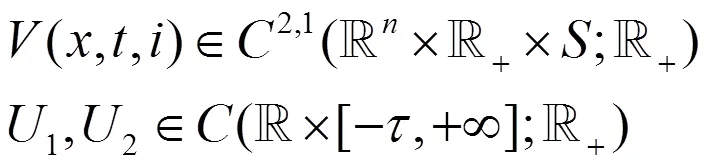
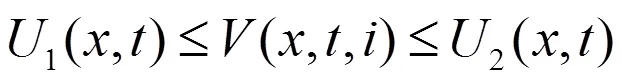
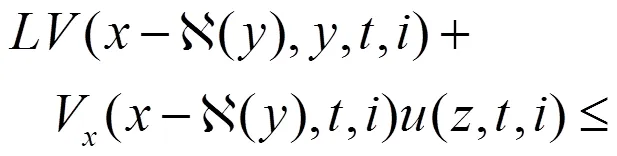
引用文献[19]的结论作为引理。

2 主要结论

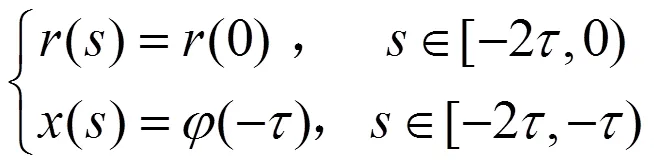
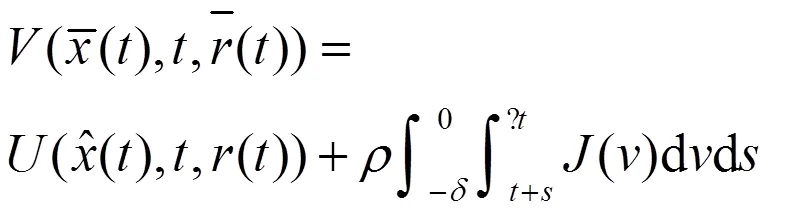
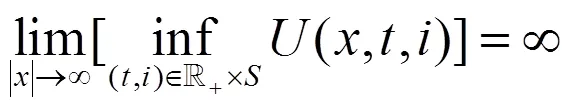
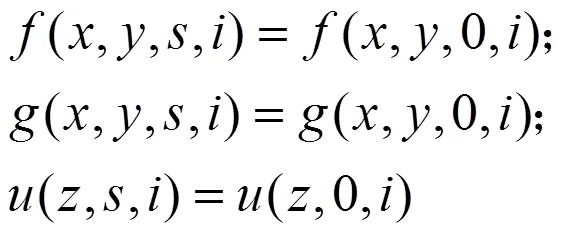
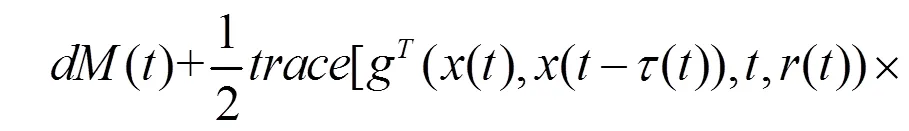
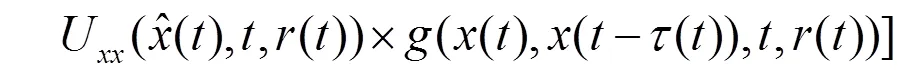
整理式（12），可以得到：

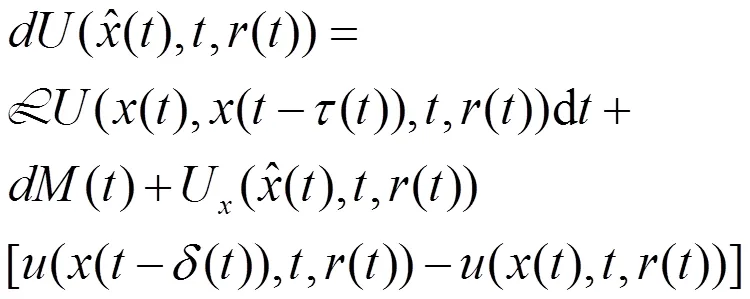
可以得到以下的结论。

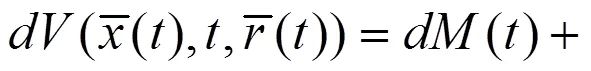
其中

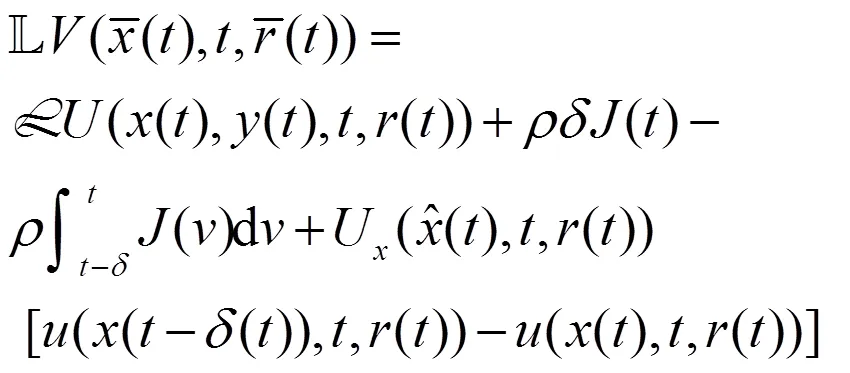
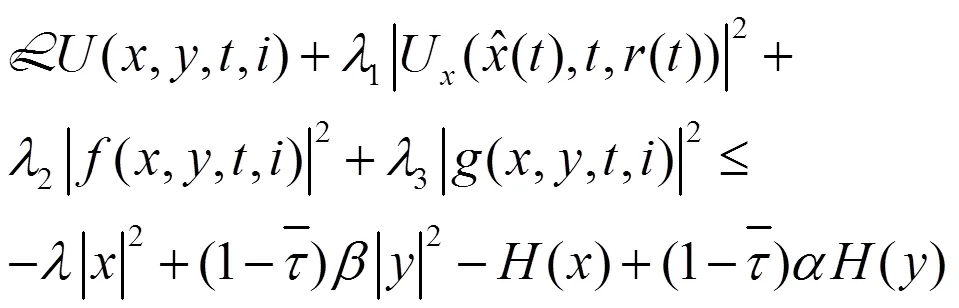
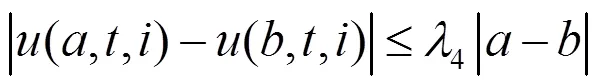
定理1 在假设1，2，3，4，6，7成立的条件下，假设

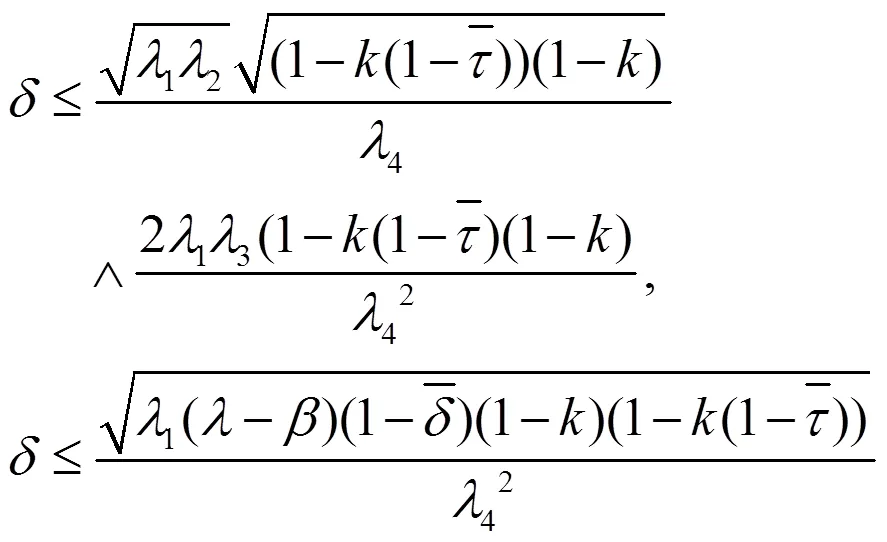
对于任意的初值(2)，系统(3)的解满足

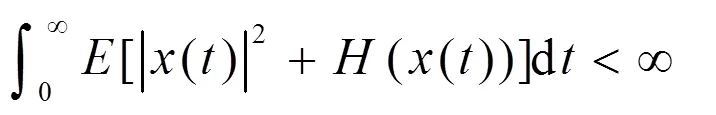
并且有

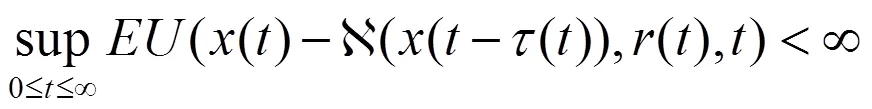
证明

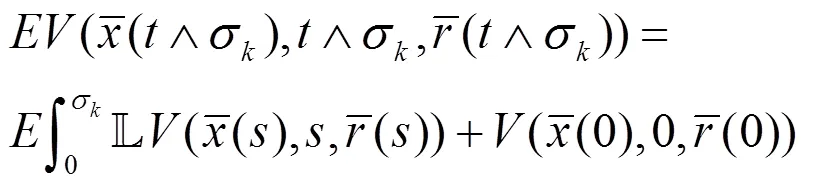
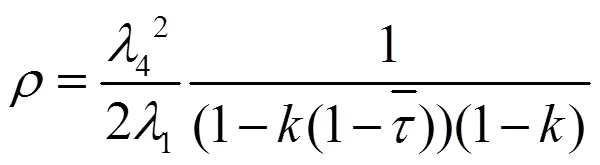
从假设7，可以得到

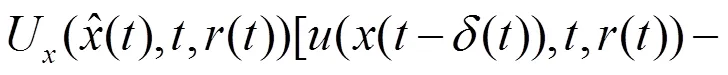
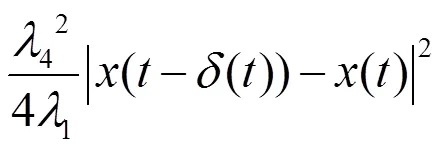
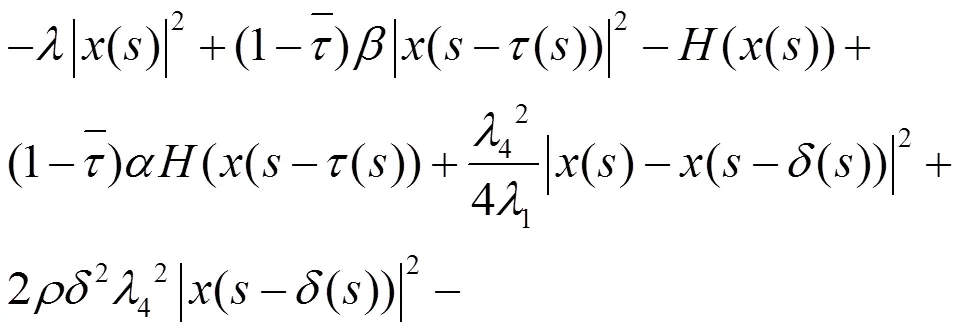
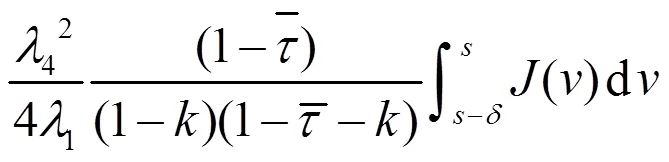
联立(19)和(20)式，可以推出

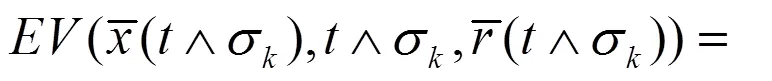
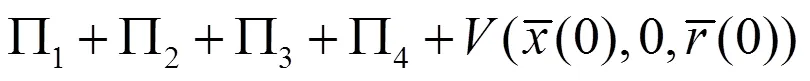
其中，

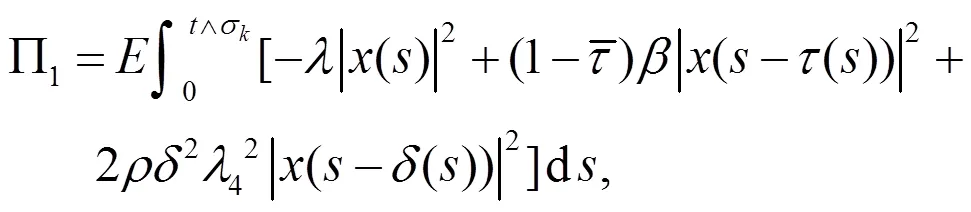
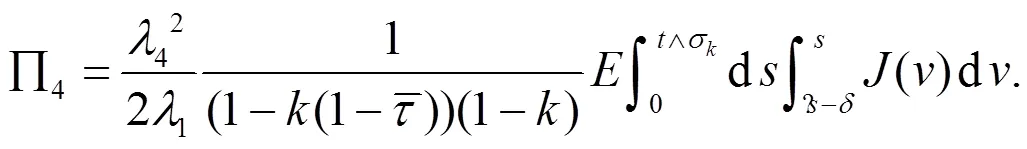
由于

因此，

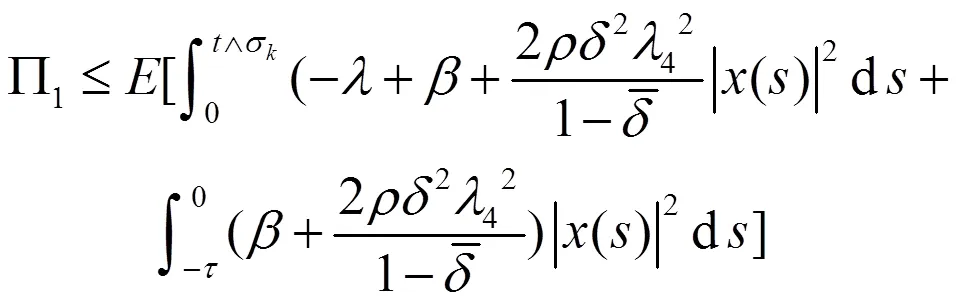
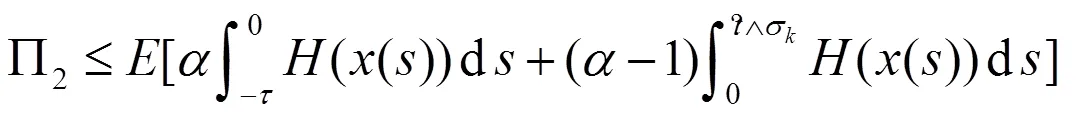
将(22)式代入(21)式中，可得

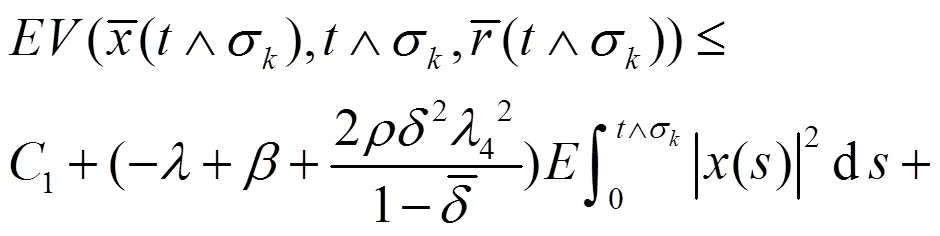
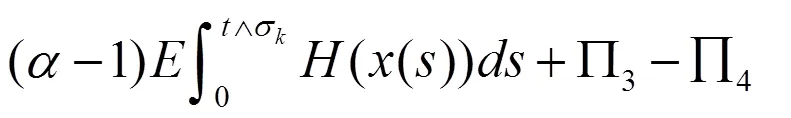
其中，

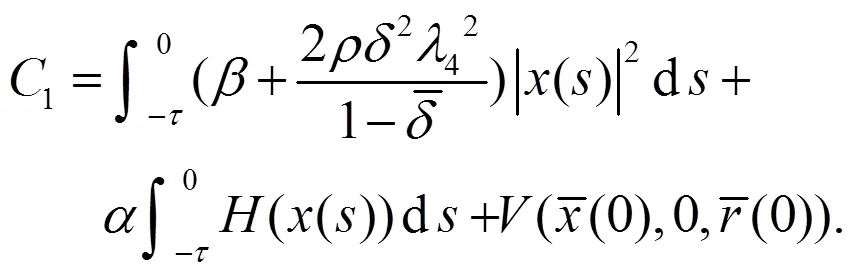
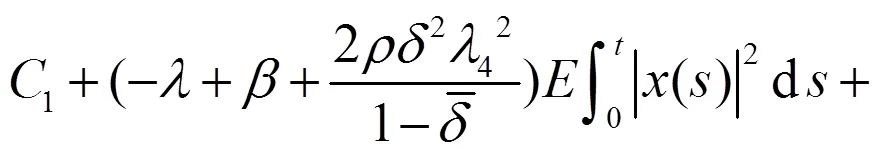
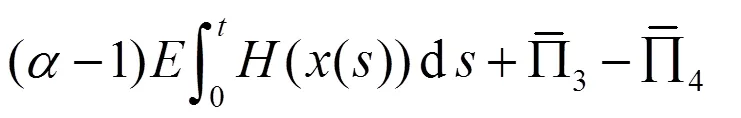
其中，

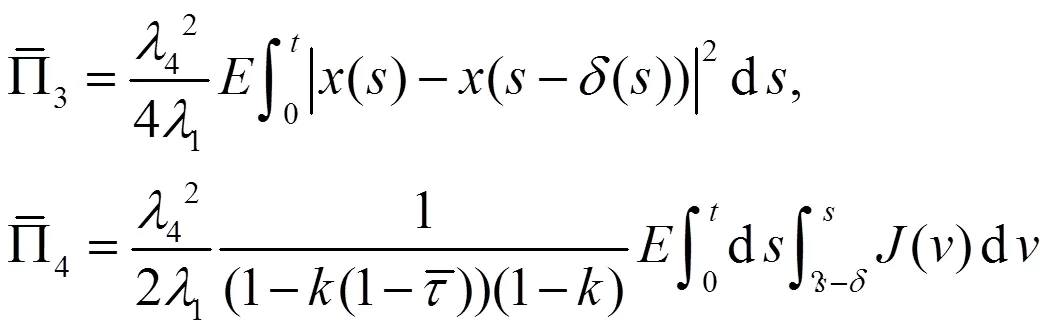
由富比尼定理可以得到

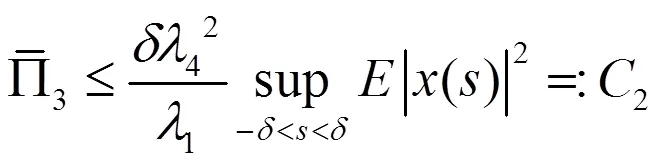
由于

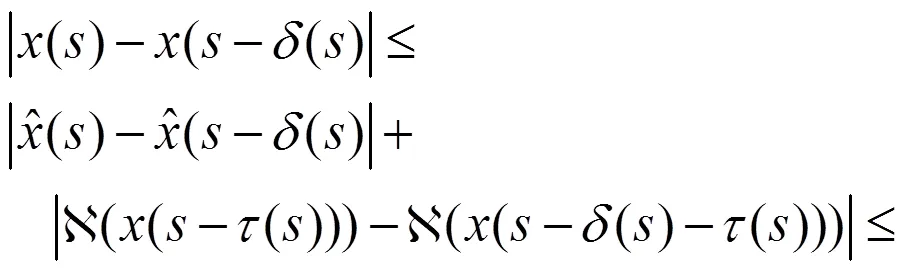
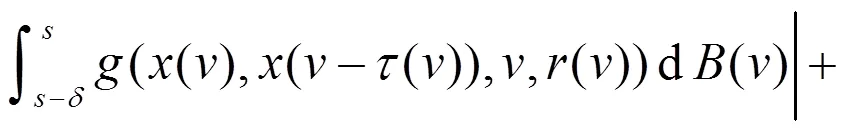
那么，由假设4，可以推出

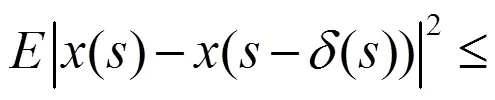
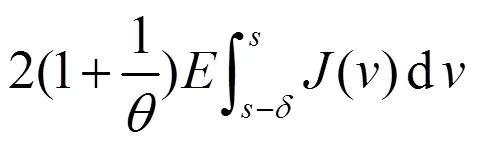
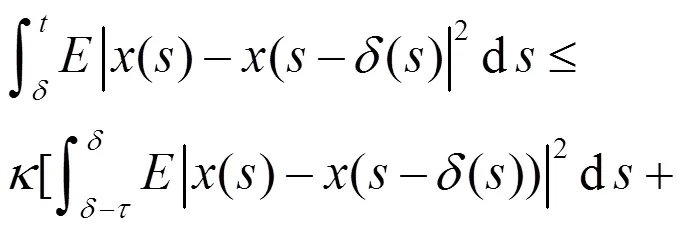
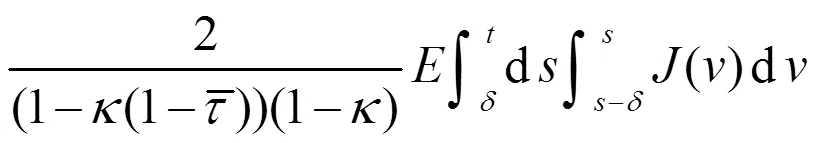
由于

因此，

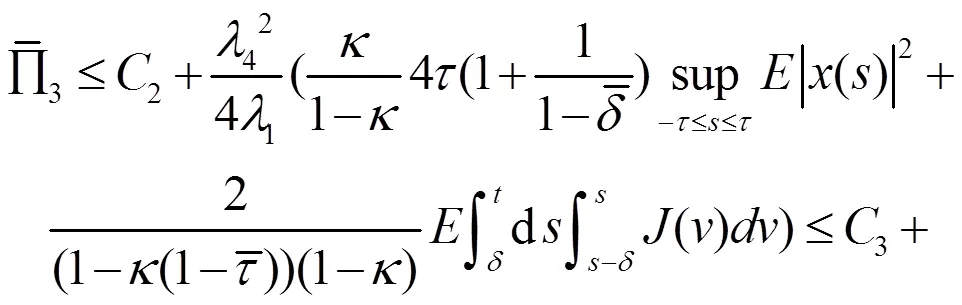
(26)

其中，

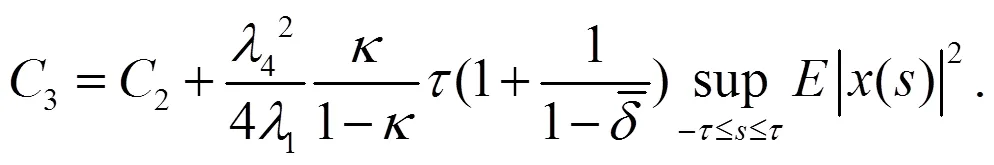
从(23)式，得到：

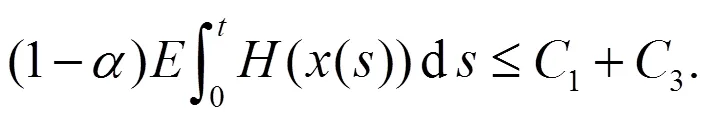
同样可以从(13)和(25)式中可以推出

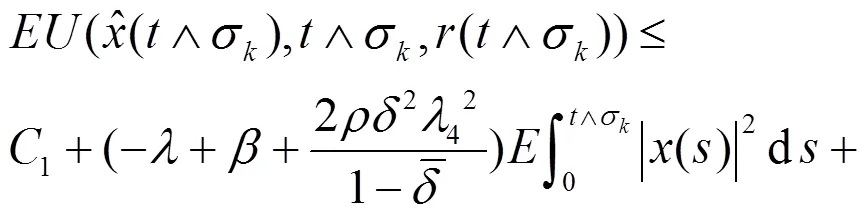
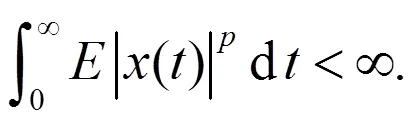
由(17)式可以得到此推论。

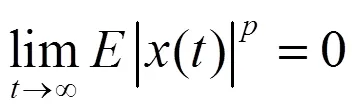
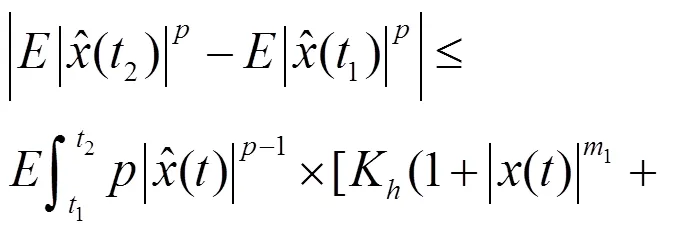
从(27)式可以得到，

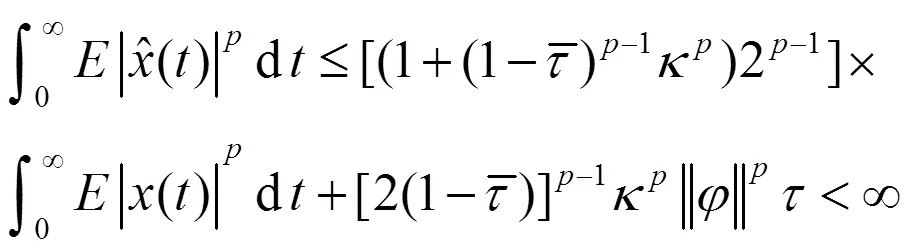
由假设4，可以推断出

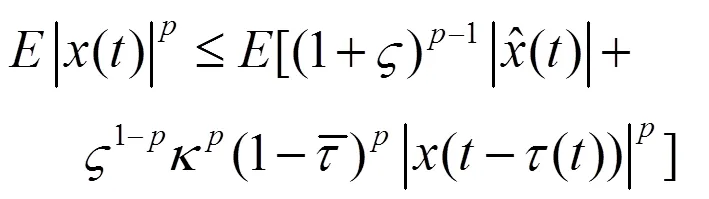
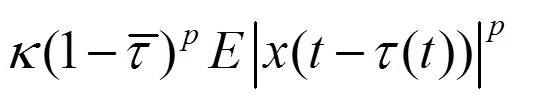
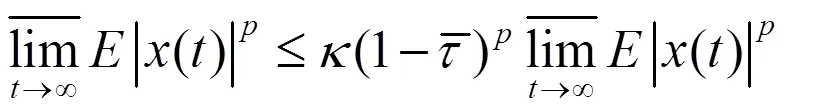
3 例子

为了说明结论的有效性，举例如下。

考虑一维变时滞混合中立型随机延迟微分方程：

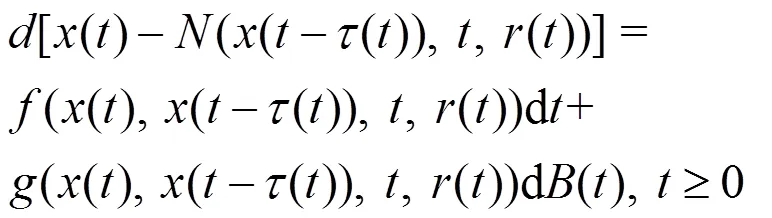
此时，令

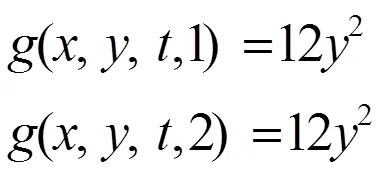
显然，不满足线性增长条件。

使用Euler-Maruyama方法对随机系统进行离散化处理，用Matlab模拟以上随机系统。

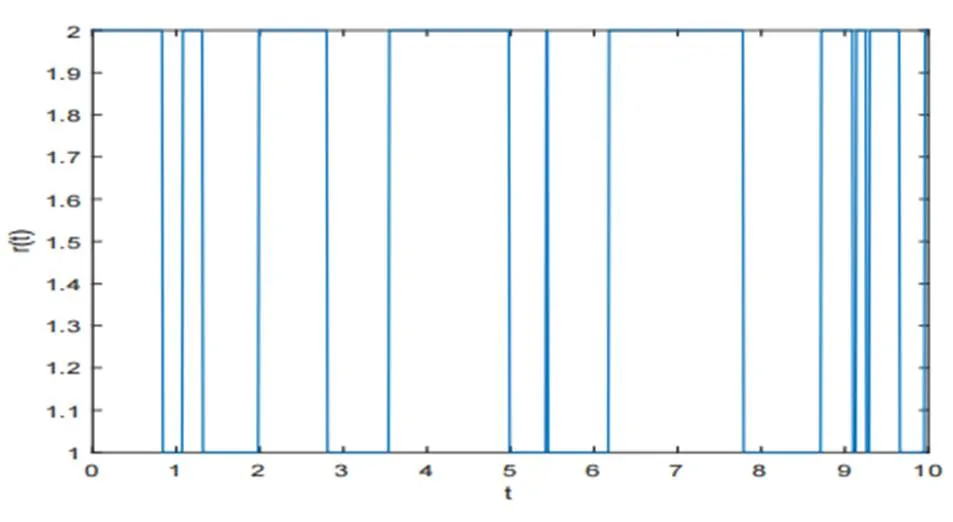
图1 马氏链的样本路径

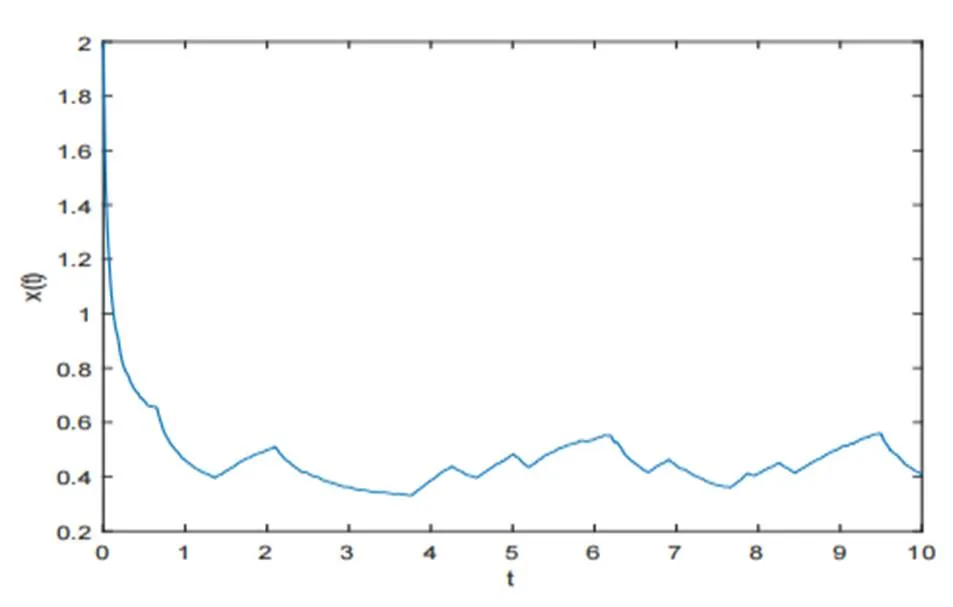
图2 当时系统(33)的样本路径（使用了Euler-Maruyama的方法且步长为0.01）

本研究的目的是设计一个反馈控制使不稳定的系统(33)变得稳定。

使用混合的NSDDE(33)，定义控制函数：

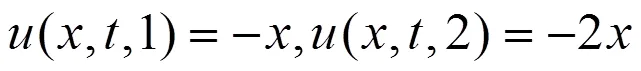
由控制函数控制的系统(3)则具有以下形式

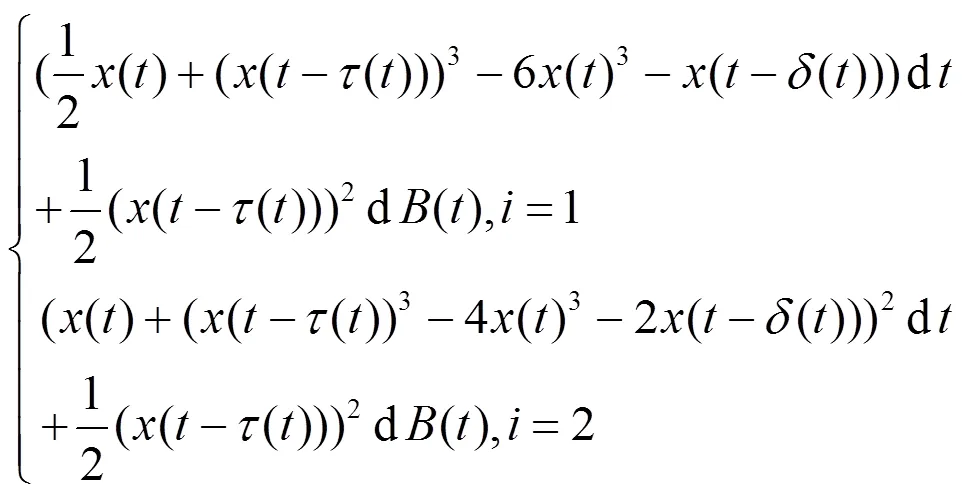
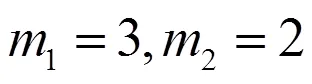
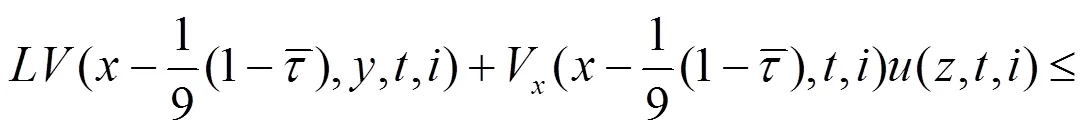
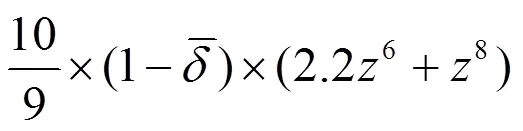
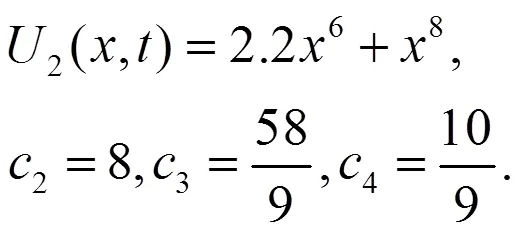
接下来，证明假设6，定义

可以得到

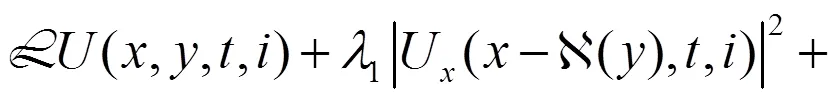
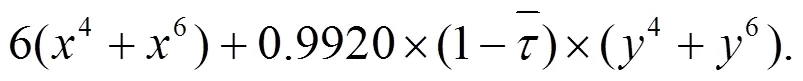
从而有

由定理1，可以推断出系统(36)的解满足

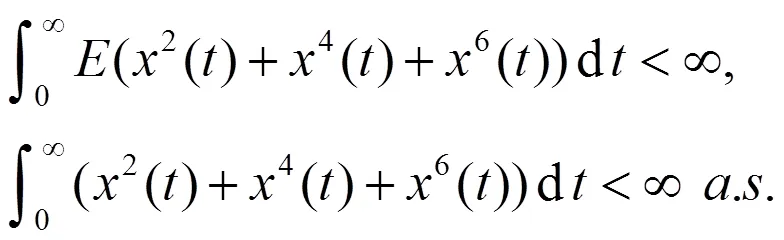
综上，可以看出在加了反馈控制函数后的随机系统的解变得稳定，即证得结论的有效性。

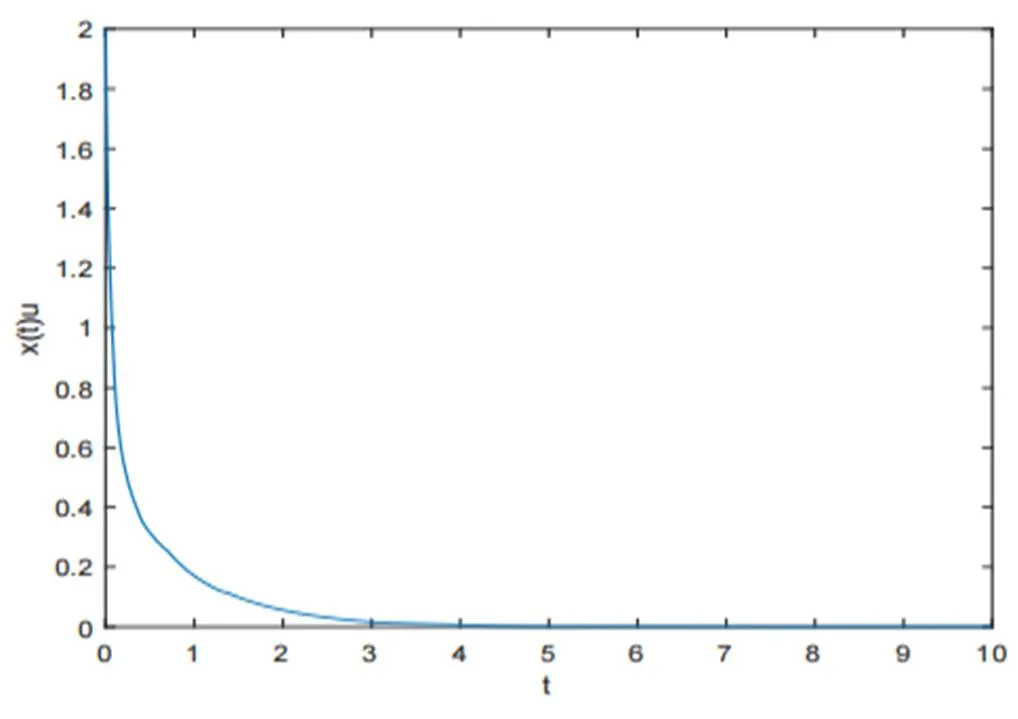
图3 当时系统(36)的样本路径(使用了Euler-Maruyama的方法，样本数1000且步长为0.01)

4 结论

[1] Mao X. Attraction, stability and boundedness for stochastic differential delay equations[J]. Nonlinear Analysis:Theory, Methods & Applications,2001,47(7):4795-4806.

[2] Yin W, Ren Y. Asymptotical boundedness and stability for stochastic differential equations with delaydriven by g-brownian motion[J]. Applied Mathematics Letters, 2017,74:121-126.

[3] Bao Z, Tang J, Shen Y, et al. Equivalence of pth moment stability between stochastic differential delay equations and their numerical methods[J]. Statistics & Probability Letters, 2021,168:108952.

[4] Hu W, Zhu Q. Stability analysis of impulsive stochastic delayed differential systems with unbounded delays[J]. Systems & Control Letters, 2020,136:104606.

[5] Mao X, Yuan C. Stochastic Differential Equations with Markovian Switching[M], London: Imperial College Press,2006.

[6] Zhang T. The stability with a general decay of stochastic delay differential equations with markovian switching[J]. Applied Mathematics and Computation, 2019,359:294-307.

[7] Du N H, Dang N H, Dieu N T. On stability in distribution of stochastic differential delay equations with markovian switching[J]. Systems & Control Letters, 2014,65:43-49.

[8] Li B, Li D, Xu D. Stability analysis for impulsive stochastic delay differential equations with markovian switching[J]. Journal of the Franklin Institute, 2013,350(7):1848-1864.

[9] Fei C, Shen M, Fei W, et al. Stability of highly nonlinear hybrid stochastic integro-differential delay equations[J]. Nonlinear Analysis: Hybrid Systems, 2019,31:180-199.

[10] Rathinasamy K B A. Mean-square stability of milstein method for linear hybrid stochastic delay integro, differential equations[J]. Nonlinear Analysis: Hybrid Systems, 2008(2):1256-1263.

[11] Hu L, Mao X, Shen Y. Stability and boundedness of nonlinear hybrid stochastic differential delay equations[J]. Systems & Control Letters, 2013,62 (2):178-187.

[12] Fei W, Hu L, Mao X , et al. Delay dependent stability of highly nonlinear hybrid stochastic systems[J].Automatica, 2017,82: 165-170.

[13] Lygeros J, Mao X, Yuan C. Stochastic hybrid delay population dynamics [M]. Springer:Heidelberg, 2006:436-450.

[14] Fei W, Hu L, Mao X, et al. Generalized criteria on delay-dependent stability of highly nonlinear hybrid stochastic systems[J]. International Journal of Robust and Nonlinear Control, 2019(5): 1201-1215.

[15] Wu A, You S, Mao W, et al. On exponential stability of hybrid neutral stochastic differential delay equations with different structures[J]. Nonlinear Analysis: Hybrid Systems,2021, 39:100971.

[16] Shen M, Fei W, Mao X, et al. Stability of highly nonlinear neutral stochastic differential delay equations[J]. Systems &Control Letters, 2018, 115: 1-8.

[17] Li X, Mao X. A note on almost sure asymptotic stability of neutral stochastic delay differential equationswith markovian switching[J]. Automatica, 2012, 48(9):2329-2334.

[18] Mao X, Shen Y, Yuan C. Almost surely asymptotic stability of neutral stochastic differential delay equations with markovian switching[J]. Stochastic Processes and their Applications, 2008,118 (8): 1385-1406.

[19] Shen M, Fei C, Fei W, et al. Boundedness and stability of highly nonlinear hybrid neutral stochastic systems with multiple delays[J]. Science China Information Sciences, 2019, 62 (10): 202205.

[20] Li X, Mao X. Stabilisation of highly nonlinear hybrid stochastic differential delay equations by delay feedback control[J]. Automatica, 2020, 112:108657.

[21] Mao X, Lam J, Huang L. Stabilisation of hybrid stochastic differential equations by delay feedback control[J]. Systems & Control Letters, 2008, 57(11):927-935.

[22] Wang P, Feng J, Su H. Stabilization of stochastic delayed networks with markovian switching and hybrid nonlinear coupling via aperiodically intermittent control[J]. Nonlinear Analysis:Hybrid Systems, 2019, 32:115-130.

[23] Chen W, Xu S, Zou Y. Stabilization of hybrid neutralstochastic differential delay equations by delay feedback control[J]. Systems & Control Letters, 2016, 88:1-13.

[24] Shen M, Fei C, Fei W, et al. Stabilisation by delay feedback control for highly nonlinear neutral stochastic differential equations[J]. Systems & Control Letters, 2020, 137:104645.

[25] Song R, Wang B, Zhu Q. Delay-dependent stability of nonlinear hybrid neutral stochastic differential equations with multiple delays[J]. International Journal of Robust and Nonlinear Control, 2021, 31(1):250-267.

STABILIZATION OF THE HYBRID NEUTRAL STOCHASTIC DIFFERENTIAL EQUATIONS CONTROLLED BY THE TIME-VARYING DELAY FEEDBACK

*ZHOU Zhi-wei，SONG Rui-li

（Nanjing University of Finance and Economics, Nanjing, Jiangsu 210023, China）

There are many research results on the quantization of quantum entanglement, but many of the existing entanglement measures are still difficult to calculate. In the paper “Entanglement measures based on observable correlations”, LUO Shun-long proposed an observable correlation measure of bipartite quantum states based on mutual information, and obtained a class of entanglement measures of bipartite quantum states. In this paper, we generalize the entanglement measure of the bipartite system to the multipartite composite quantum system, and prove that it satisfies the necessary physical conditions of entanglement measure.

multipartite quantum system; quantum states; observable correlations; mutual information; entanglement measure

1674-8085（2022）03-0006-09

O175

A

10.3969/j.issn.1674-8085.2022.03.002

2021-12-01；

2022-01-25

国家自然科学基金项目(61773217)

*周之薇(1995-)，女，陕西西安人，硕士生，主要从事概率论与数理统计的研究(E-mail:412481190@qq.com).