异方差分层线性模型的A-最优设计

陈佳颖，刘 欣

(东华大学 理学院，上海 201620)

分层线性模型也称混合效应模型或随机系数模型，是同时考虑观测对象的群体效应和个体效应的两阶段模型，通常用于对多个个体重复测量的数据进行建模。其理论分析日臻完善，主要有Vonesh等[1]和Verbeke等[2]的研究。

随着分层线性模型在经济学、药物动力学、心理学等方面的广泛应用，关于分层线性模型的最优试验设计问题得到了持续关注。在观测误差为同方差的场合已有不少研究结果。在群体参数方面：Fedorov等[3]建立了刻画D-最优设计的等价性定理，随后Schmelter[4-5]、Debusho等[6-7]在这方面做了一系列研究。在个体参数方面：Prus等[8]研究了D-最优设计和线性最优设计，随后Prus[9-10]讨论了G-最优设计和极小极大设计，He等[11]考虑了R-最优设计。

实际中，观测误差为异方差的情况经常出现，针对异方差模型的分析也是统计研究的重点之一。对于异方差分层线性模型的研究工作目前较少，Cheng等[12]研究了群体参数的D-、G-、A-、I-最优设计问题，获得了随机系数一次回归模型的最优设计。Liu等[13]考虑了个体参数的D-最优设计问题，给出了D-最优设计的充分必要条件。

本文研究分层线性模型中的最优设计问题，与大多数现有文献不同，本文考虑的是异方差模型。讨论个体参数的最优设计，并选择研究目前结论尚少的A-最优设计。同时，通过计算效率将最优设计和等权重设计进行了比较。

1 异方差分层线性模型和预备知识

假设在设计区域χ上，对n个个体进行重复观测，其中对个体i观测mi次，并用yij表示第i个个体的第j次观测值。本文考虑的异方差分层线性模型如下：

yij=fT(xij)βi+ε(xij)，j=1,2,…,mi,

i=1,2,…,n

(1)

式中：xij∈χ表示试验条件；f=(f1,…,fp)T表示已知的回归函数向量；随机向量βi=(βi1,…,βip)T为个体i的个体参数；ε(xij)为随机误差。此外，模型满足：

(1)E(βi)=β=(β1,…,βp)T，Cov(βi)=σ2D,i=1,2,…,n；

(2)E(ε(xij))=0,var(ε(xij))=σ2/λ(xij),j=1,2,…,mi,i=1,2,…,n；

(3)不同个体的观测值、个体参数向量和观测误差都不相关。

其中，总体平均值β未知，σ2已知，λ(x)是定义在设计区域χ上的正实值函数。

当λ(x)恒等于1时，模型(1)就是Prus等[8]研究的同方差分层线性模型。

(2)

(3)

式中：In为n×n单位矩阵；Jn为所有元素等于1的n×n矩阵；⊗表示矩阵的Kronecker积。

2 个体参数的A-最优设计

本节以个体参数的精准预测为目标讨论最优设计问题。

参照Prus等[8]的做法，本文考虑Kiefer[14]定义的近似设计为

(4)

式中：支撑点x1,x2,…,xk给出观测的条件，而权重w1,w2,…,wk表示在这些点上进行的总观测次数的相对比例。对于近似设计ξ，其在模型(1)下的标准化信息矩阵可定义为

(5)

相应地，对于近似设计ξ，式(3)中定义的均方误差矩阵可表示为

(6)

式中：Δ=mD。特别地，当D是非奇异的时，式(6)可简化为

(7)

(8)

当D是非奇异时，A-准则函数简化为

tr{(Mλ(ξ)+Δ-1)-1}

(9)

记Ξ为设计空间中所有具有非奇异信息矩阵的近似设计的全体。如果设计ξ*使得式(8)达到最小，即

(10)

则ξ*称为个体参数的A-最优设计。

下文的等价性定理给出了一个设计为A-最优的充分必要条件。

定理1对任一设计ξ，定义其敏感函数为

(11)

则设计ξ*是个体参数的A-最优设计当且仅当

(12)

此外，上确界在ξ*的支撑点处达到。

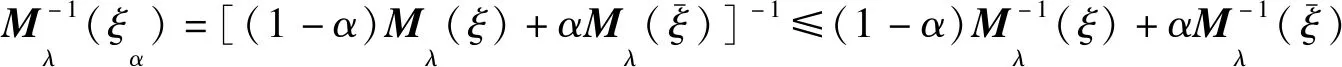
且

因此，A准则函数φpred,A(ξ)是凸的。

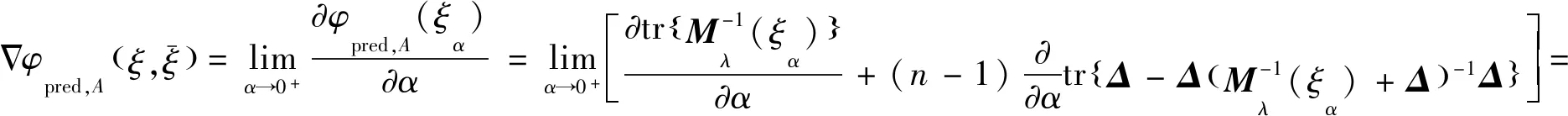
令δx是设计点为x的单点设计，根据文献[15]可知：

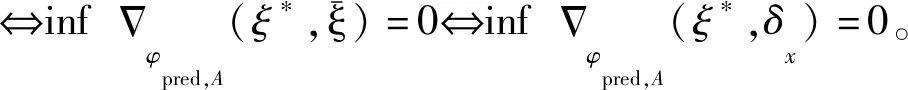
进而得到，设计ξ*∈Ξ是个体参数的A-最优设计

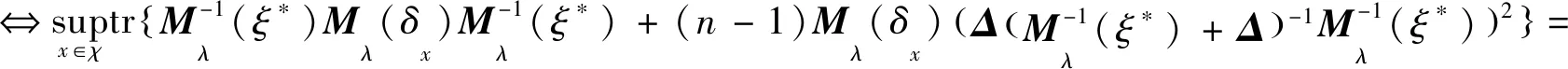
即ξ*∈Ξ是个体参数的A-最优设计当且仅当

推论1设D是非奇异的，定义设计ξ的敏感函数为

(13)

设计ξ*是个体参数的A-最优设计当且仅当

(14)

此外，上确界在ξ*的支撑点处达到。

例1随机截距一次回归模型的A-最优设计。

考虑χ=[0,1]上的随机截距一次回归模型：

yij=βi1+β2xj+ε(xj)

(15)

式中：βi1是均值为β1、方差为σ2d1的随机截距。对此模型，p=2,f(x)=(1,x)T且矩阵D=diag(d1,0)。

Chang[16]在研究加权多项式回归模型的D-最优设计问题时考虑了如式(16)所示的方差权重函数。

(16)

在这一权重函数下，Cheng等[12]求出了随机斜率一次回归模型的群体参数的D-最优设计。

下面在此权重函数下求模型(15)的个体参数的A-最优设计。首先，根据Cheng等[12]研究中的引理3.1可以确定A-最优设计有两个支撑点，分别是x1=0,x2=1，即A-最优设计具有如式(17)所示的形式。

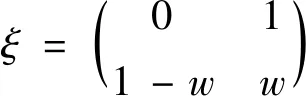
(17)

其中w∈[0,1]为待定的权重参数。形如式(17)的设计所对应的A-最优准则函数为

对准则函数求导并令其等于0，得到方程：

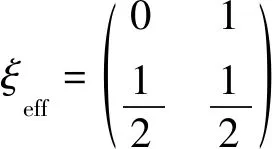
(18)

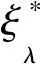
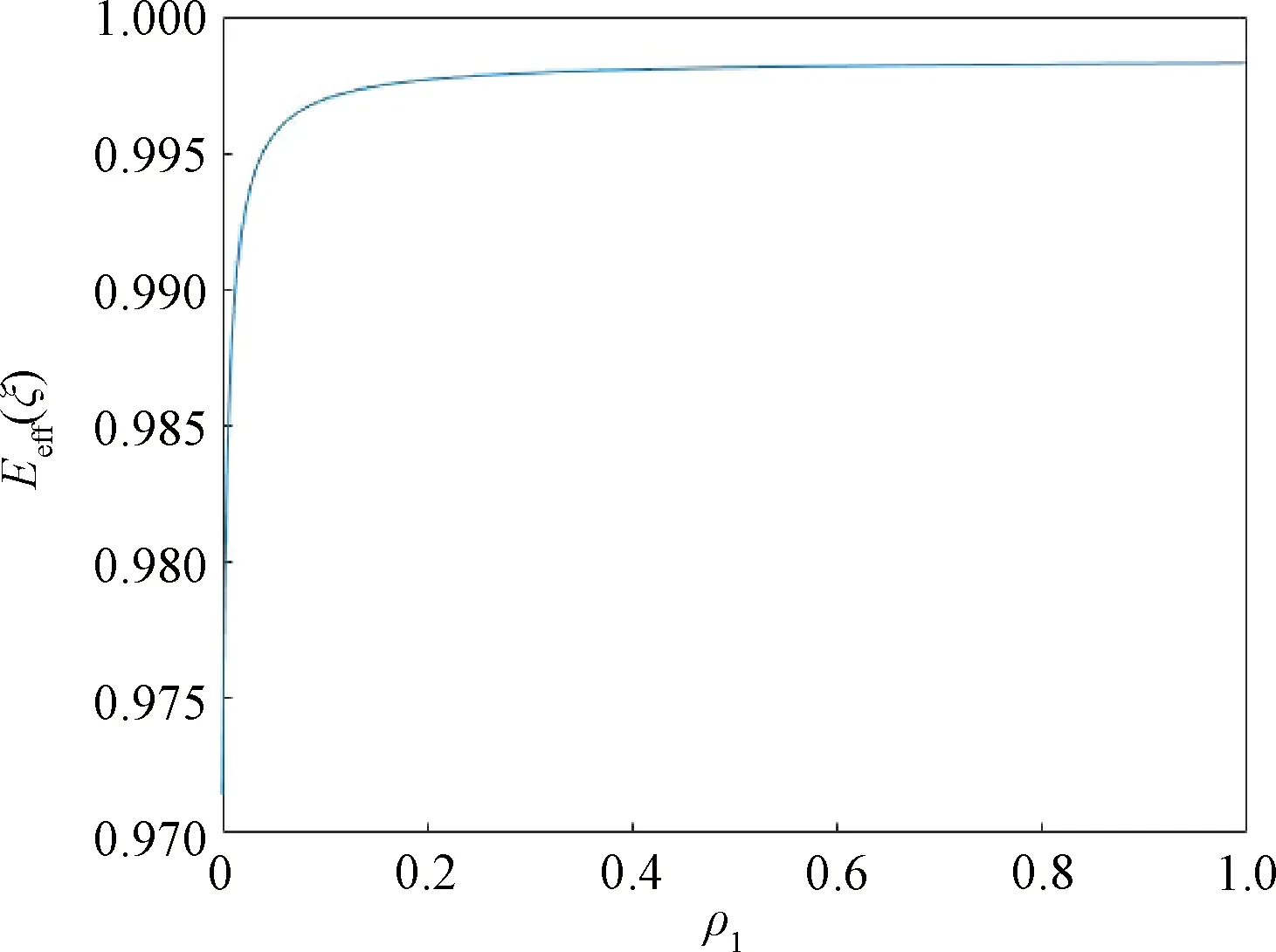
图1 等权重设计ξeff相对于A-最优设计的效率图Fig.1 Efficiency of equireplicated design ξeff relative to A-optimal design

例2随机斜率一次回归模型的A-最优设计。

考虑χ=[0,1]上的随机斜率一次回归模型：

yij=β1+βi2xj+ε(xj)

(19)

式中:只有斜率βi2是随机的，其均值为β2，方差为σ2d2，因此矩阵D=diag(0,d2)。

Cheng等[12]也给出了权重函数为

λ2(x)=x2+1

(20)

时，模型(19)的群体参数的几类最优设计。

现在来求其个体参数的A-最优设计，求解方法同例1，只需考虑形如式(17)的两点设计。

此时A-准则函数为

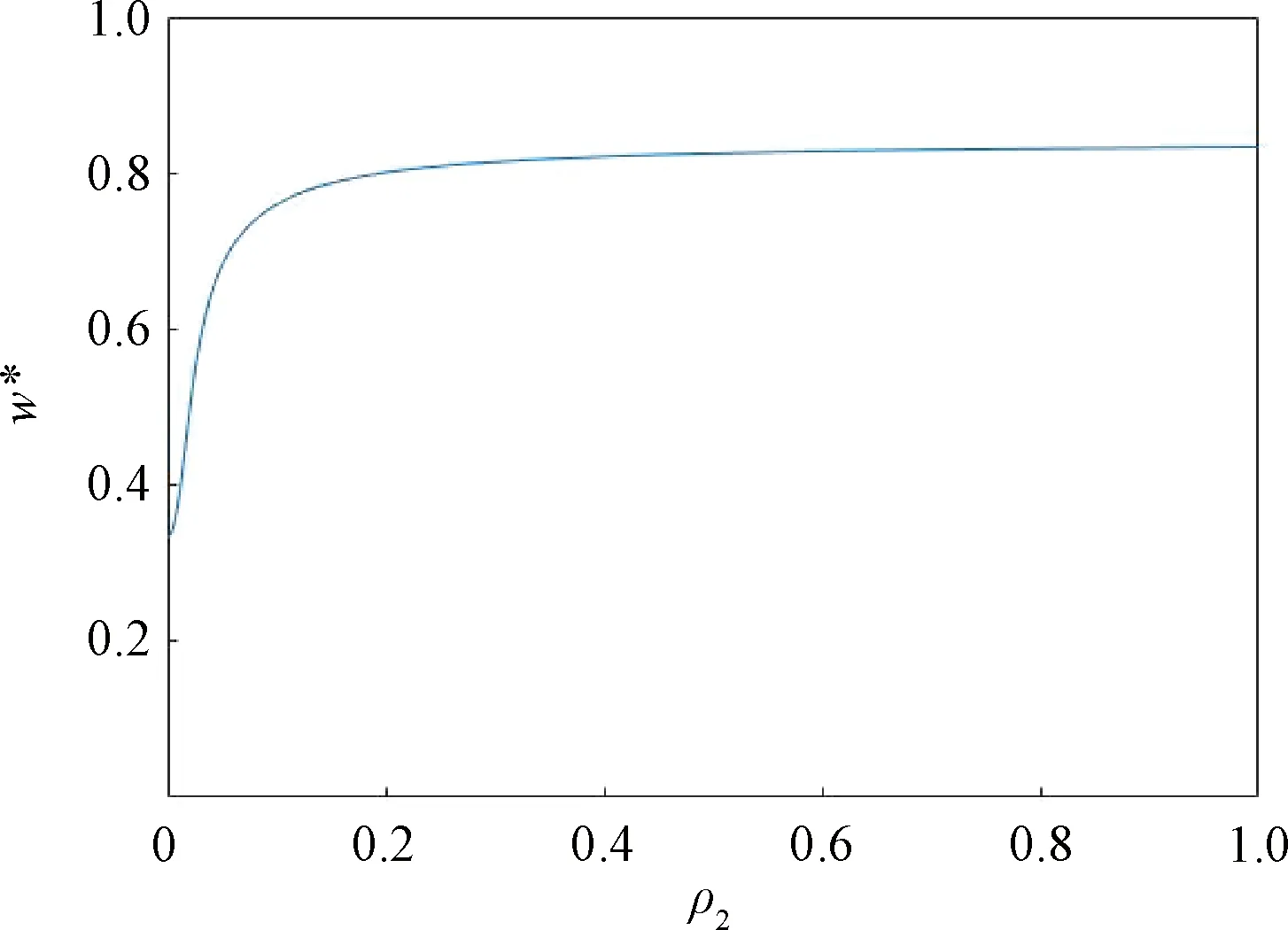
图2 随机斜率一次回归模型的A-最优设计的权重函数(异方差结构为λ2(x))Fig.2 Weight function of A-optimal design for the straight line regression with random slope (heteroskedasticity structure is λ2(x))

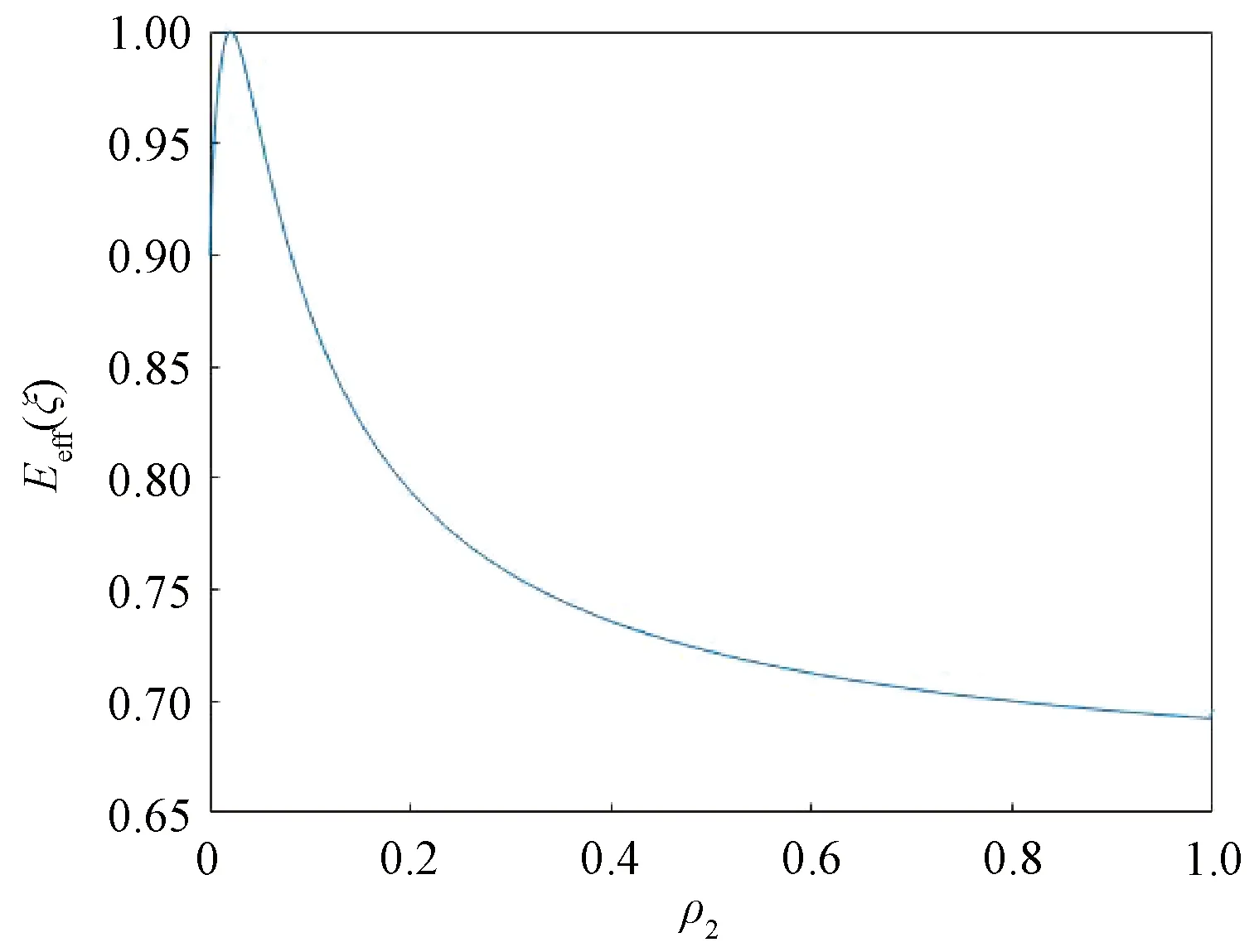
图3 等权重设计ξeff相对于A-最优设计的效率图Fig.3 Efficiency of equireplicated design ξeff relative to A-optimal design