一种超宽带随机噪声压缩感知雷达成像方法
2022-05-12王冰洁
程 蒙,王冰洁
(太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024)
0 引 言
超宽带雷达具有较高的距离分辨率,现已广泛应用于近距离传感领域中,超宽带噪声雷达由于其信号源的噪声特性,因此具有较低的可截获性和较强的抗电磁干扰能力,近年来受到重视。在目标定位和目标测速中,超宽带噪声雷达的有效性已经得到证实,其距离向分辨率与信号带宽有关,速度分辨率与观测累计时间有关。在合成孔径雷达(Synthetic Aperture Radar,SAR)成像方面超宽带噪声雷达也备受关注,其成像算法与传统线性调频信号基本相同,不同之处在于快时间域的脉冲压缩,以及在慢时间域超宽带随机信号雷达的多普勒相位历程具有随机性,而线性调频信号则是固定变化的。
压缩感知(Compressive Sensing,CS)理论正式提出于2006 年,后被广泛应用于信号处理各领域。压缩感知采样打破了传统奈圭斯特采样定律,可以显著地降低信号的采样速率和样本集的数量,极大地减少了硬件系统的代价,因此人们尝试将CS 理论应用到超宽带噪声雷达中以解决其高带宽带来的硬件负担。在SAR 成像方面,近年来提出了基于CS 的不同成像算法,可以用于提高成像分辨率或降低需要采集的数据量,并且引入自聚焦方法用于消除不确定相位误差。而基于CS 的超宽带SAR 在降低信号采集带宽的同时,具有很好的抗电磁干扰能力。
大量工作表明,CS 理论在超宽带噪声雷达应用中,在系统硬件和处理效果上均具有优点,然而对于SAR成像,随着成像尺寸的增加,CS 重构算法的复杂性将会凸显,通常远远高于传统线性成像算法,这为成像算法的设计带来一定的困难。
文献[20]利用正则化方法完成了基于CS的聚束模式SAR 成像,本文在此基础上,提出了一种采用超宽带噪声信号源的聚束模式SAR成像算法。与传统信号源雷达不同,首先它需要利用方程组求逆,获得一维距离向信息,然后通过CS方法对二维场景进行重建。该方法相对于传统线性成像算法的优点在于,它可以避免因使用噪声信号源,导致的在慢时间域中非一致多普勒相位产生的成像误差。同时考虑到算法复杂性,本文提出了零延拓近似算法,通过在重建算法的迭代中利用二维FFT和快速小波变换,实现快速计算矩阵和向量的乘法。仿真结果表明,这种近似算法在极大地降低运算量和内存消耗的同时,保持着较好的运算精度,可以完成对大尺度场景的成像任务。
1 基本原理
1.1 CS 理论
CS 理论主要研究稀疏信号的重建及其可重建条件,稀疏信号可以通过较少的非自适应测量集准确重建。其数学描述为:∈R为观测向量,它与未知稀疏信号∈R有如下关系:

式中,∈R,为感知矩阵,是对未知信号进行的线性测量。当<时,上述方程组是欠定的,CS 理论指出,当满足约束等距(RIP)条件时,仍然可以准确通过下式进行重建:

式中为施加的一正则化约束参量。上述优化问题是凸的,可以将其转化为线性规划进行求解,如基追踪算法,也可通过贪婪算法如匹配追踪算法等。本文采用内点法进行求解,它是解凸优化问题的一种常用方法,具有较高的精度和运算性能。
1.2 基于CS 的超宽带随机噪声雷达成像原理
1.2.1 一维距离向重建
假定()为雷达的发射信号序列,信号回波为(),由于聚束模式雷达距离向波束照射宽度是一定的,因此()可看作()通过某个阶的滑动平均(MA)模型的响应:
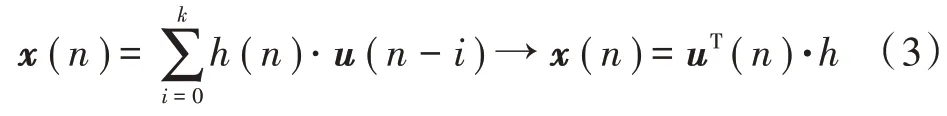
式中:()=[(),(-1),…,(-)];为系统的传递函数,对应传统的脉冲压缩结果,因此一维距离向重建为系统辨识问题。
通过采集个样本点{(),()},{(),()},…,{(i),(i)},式(3)可以构成一线性方程组:=(4)式中:[(),(),…,(i)];=[(),(),…,(i)]。对于每个样本点{(i),(i)},其采集是相互独立的。当()为确定序列时,如信号源采用伪随机数,()的采集可省略,这时只需要记录采样时间和()即可。通过这种方法,信号的采样频率可以降至很低。当成像区域只含有少量的点目标时,式(4)可以采用CS重建算法求解,它可以减少采集的样本集{,}的个数。需要指出的是,当每个样本点之间采样间隔大于+1 时,将近似为随机矩阵,它可以很好地满足RIP条件。
使用线性方程组求解的方法,相对于传统互相关的方法,不存在旁瓣掩蔽效应,如图1b)所示,采用互相关法,除了在目标处出现反射尖峰外,其他位置仍有信号波动,而图1c)为随机抽取一半的数据样本点采用CS的方法得到的结果,它可以准确重建出场景的一维反射信息。
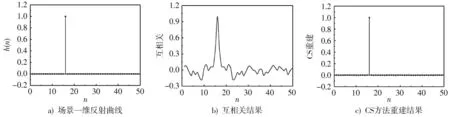
图1 互相关与CS 方法结果对比
1.2.2 基于CS 的成像原理
设超宽带随机信号雷达在观测角处经过一维重建后的记为p(),其傅里叶变换与成像场景(,)的空间(频域空间)有如下关系:
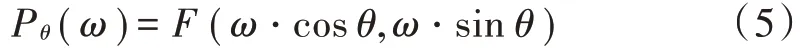
因此通过变化可以得到一系列极坐标下的场景空间采样。由于空间采样是极坐标下的,因此无法直接通过二维快速傅里叶变换对场景成像,通常需要做插值处理。
二维直角坐标系下,傅里叶变换[,]可以表示为如下形式:
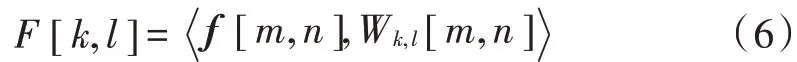
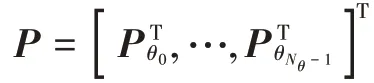
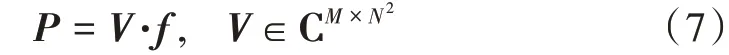
式(7)包含有复数运算,将不利于优化算法的计算,因此采用IFFT 获取式(7)的等价形式:
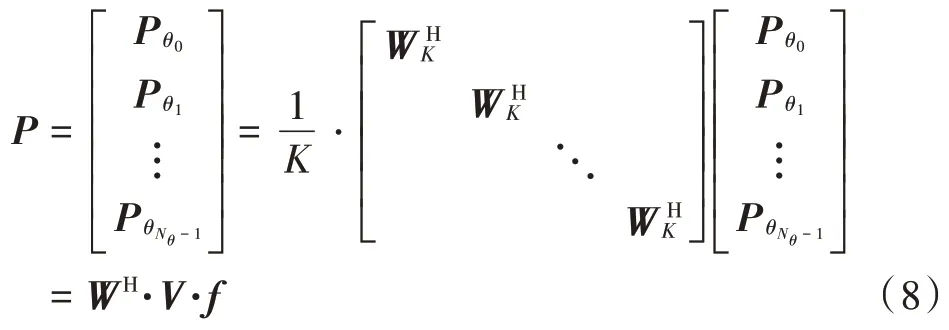
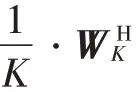
通常雷达图像在某些基下可以稀疏表示,因此有:
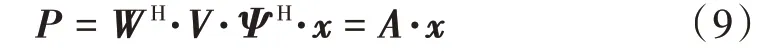
式中为稀疏表示基。因此超宽带噪声雷达成像可以转化为求解下式优化问题:
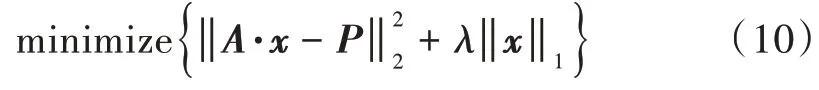
1.2.3 零延拓近似算法
在文献[22]中,内点法的每个中心点是通过牛顿法迭代获得的,它利用预处理共轭梯度算法计算海森矩阵的逆。其中海森矩阵和某一向量的乘法需要被反复运算,该乘法最终通过计算和的矩阵向量乘法实现。本文利用矩阵的特殊性,提出一种近似计算矩阵向量乘法的方法,它在极大地降低运算量的同时保持较好的计算精度,并且该方法在运算过程中不需要存储矩阵,因此可以节省大量的运算内存。
如式(9),当采用小波基作为稀疏表示基时,矩阵的乘法需要一次逆小波变换、一次的矩阵向量乘法和N次IFFT;矩阵的乘法需要N次FFT、一次的矩阵向量乘法和一次小波变换。其中最耗时的计算为和的乘法,本文采用二维快速傅里叶变换做近似计算,其方法如下。
如图2 所示,将矩阵划分为分块矩阵形式:
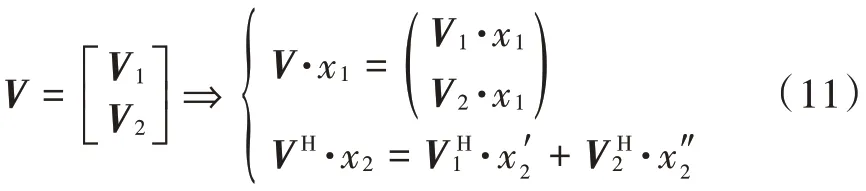
式中:采用精确计算;采用近似计算。由于可以看作向量对空间映射的变换基,因此它可以使用直角坐标系下的2D⁃FFT 基近似计算,其中近似计算的部分记作′。为了保证这种近似的精度,首先需要对[,]作零延拓处理。如图2 所示,每个P在空间中有16 个采样点,其中少量的低频部分采用计算,剩余的高频部分采用近似′计算。在′的近似计算中,首先对[,]作一倍零延拓处理,然后计算其2D⁃FFT,得到分别沿轴和轴为32 点的频域点,如图2c)中圆点所示。最后,选取最靠近精确解(三角点)的近似解(圆点)作为计算结果。对于的近似计算见式(11),可以由此类比得到。
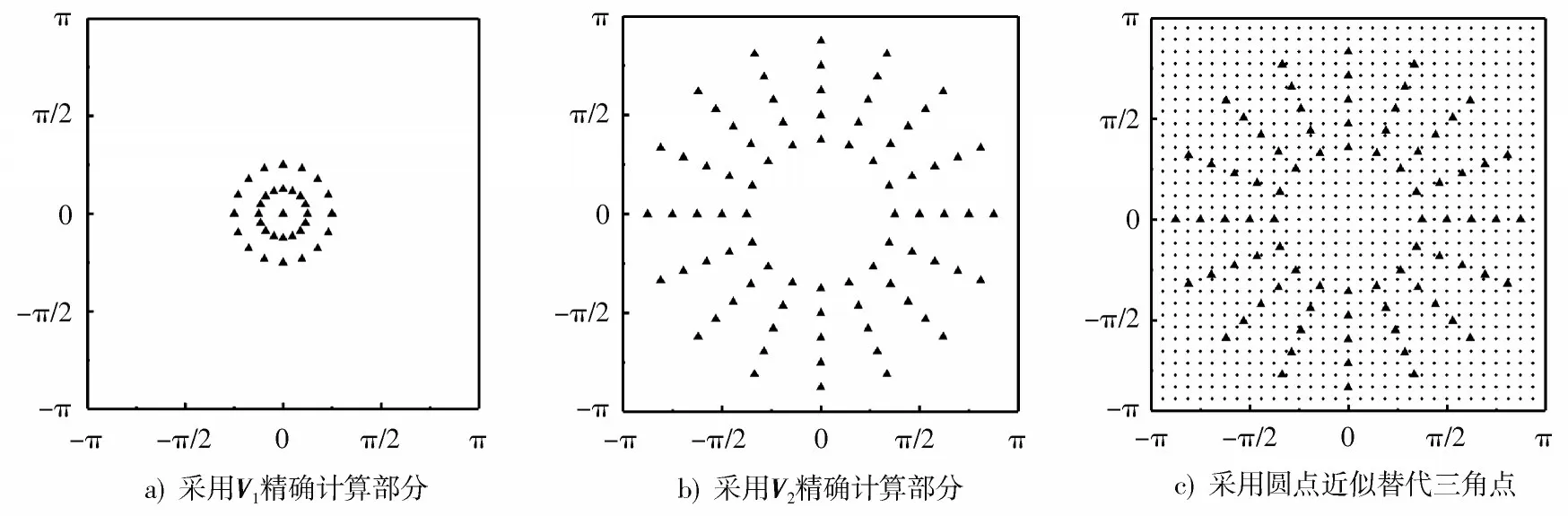
图2 零延拓近似方法示意图
当成像场景维度大于128×128 时,通常现有的计算硬件仍然无法满足部分的精确计算,将全部划分到的处理方法依然可以得到较好的结果。
2 仿真结果及性能分析
2.1 一维距离向重建
为了研究噪声对一维距离向重建算法的影响,通过仿真对两种欠采样率下使用CS 进行重建,结果如图3所示。信号源为仿真生成的带限随机过程,其中采样率和信号带宽之比为10,()的反射目标位置随机选取,大小随机设置+1 或-1,信号欠采样率定义为=,其中为总的回波信号点数,为从中随机选取的点数,并在回波中加入不同大小的白噪声得到不同信噪比(SNR)的重构结果。从结果中可看出即使噪声功率和回波功率相同时(0 dB),仍然可以得到较好结果。对比=0.5 和0.9 的结果,可以发现通过增加样本数量,算法的抗噪声性能会有所改善。
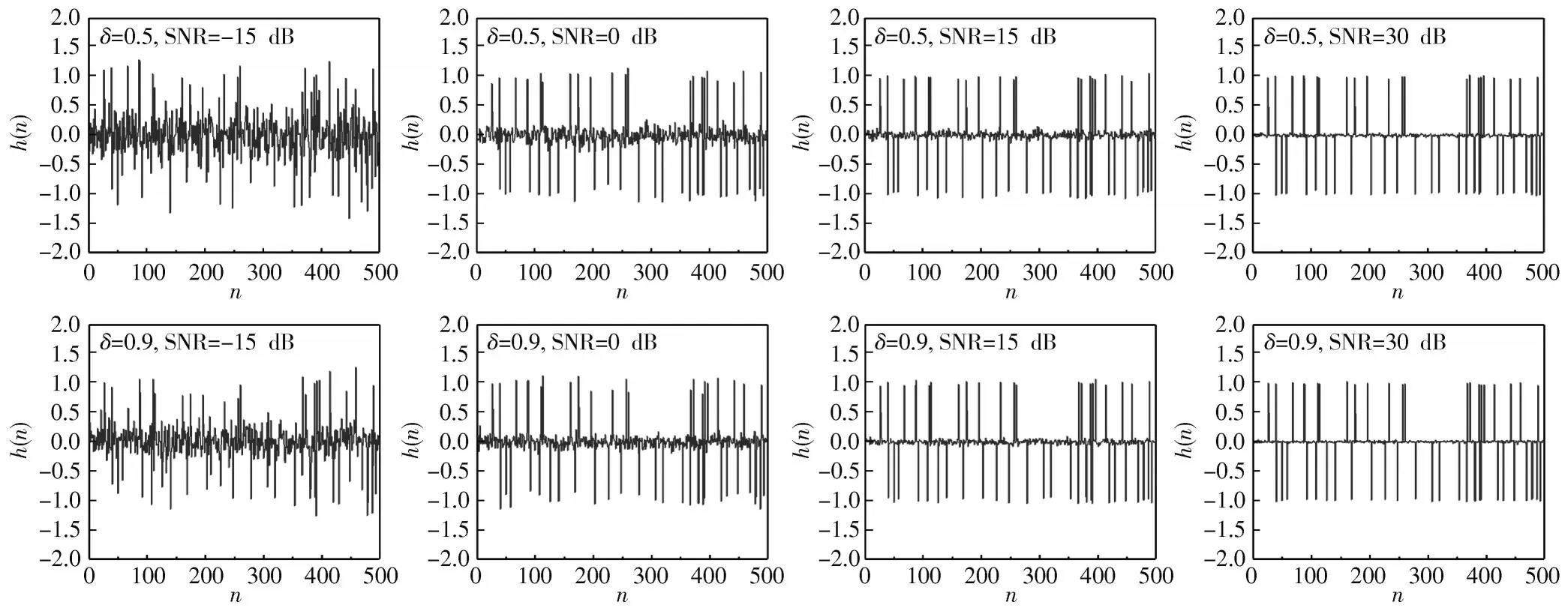
图3 欠采样率与信噪比对重建的影响
2.2 二维成像分析
首先对点反射目标场景的成像进行仿真,其中采用和文献[25]相同的滤波后向投影算法(FBP)作为经典成像算法,与本文提出的零延拓近似算法做对比。首先仿真获取场景不同观测角的一维重建数据p,然后随机抽取数量为N组的数据。对于二维数据,采用=N N作为数据的欠采样率,其中为图像横向(或纵向)的维度设为128。由于目标场景具有稀疏性,因此不需要考虑稀疏表示基。结果如图4 所示,可以看出FBP 算法在较少的数据样本下存在严重的伪影,而采用CS 的零延拓近似算法则不存在。

图4 直接稀疏场景成像对比
MSTAR 公共数据广泛应用于雷达成像算法研究中,因此对于非直接稀疏的情况,选用其中一张图片,采用上述点反射目标场景的方法进行仿真。其中零延拓近似算法中的图像稀疏表示基采用Daubechies 2 小波,结果如图5所示。可以看出采用零延拓近似算法可以得到较好的效果。由于原始图片点数为512×512,当p选取512组时,成像算法需要对2×512≈5×10个变量进行优化(其中一半是在计算中引入的),矩阵包含512×512>10个元素,现有计算硬件内存已很难满足原始的精确重建算法,而采用零延拓近似算法大约花费15 min。

图5 非直接稀疏场景成像对比
2.3 零延拓近似算法性能分析
零延拓近似算法的精确性分析,可以直观地通过分别采用精确法、直接近似法和零延拓近似算法计算矩阵·与某一向量,及其共轭转置·与的投影向量··(记为)的乘法结果进行比较。结果如图6所示,可以看出,直接使用2D⁃FFT 的近似方法和精确解法存在较大差异,经过零延拓后差异将明显缩小。
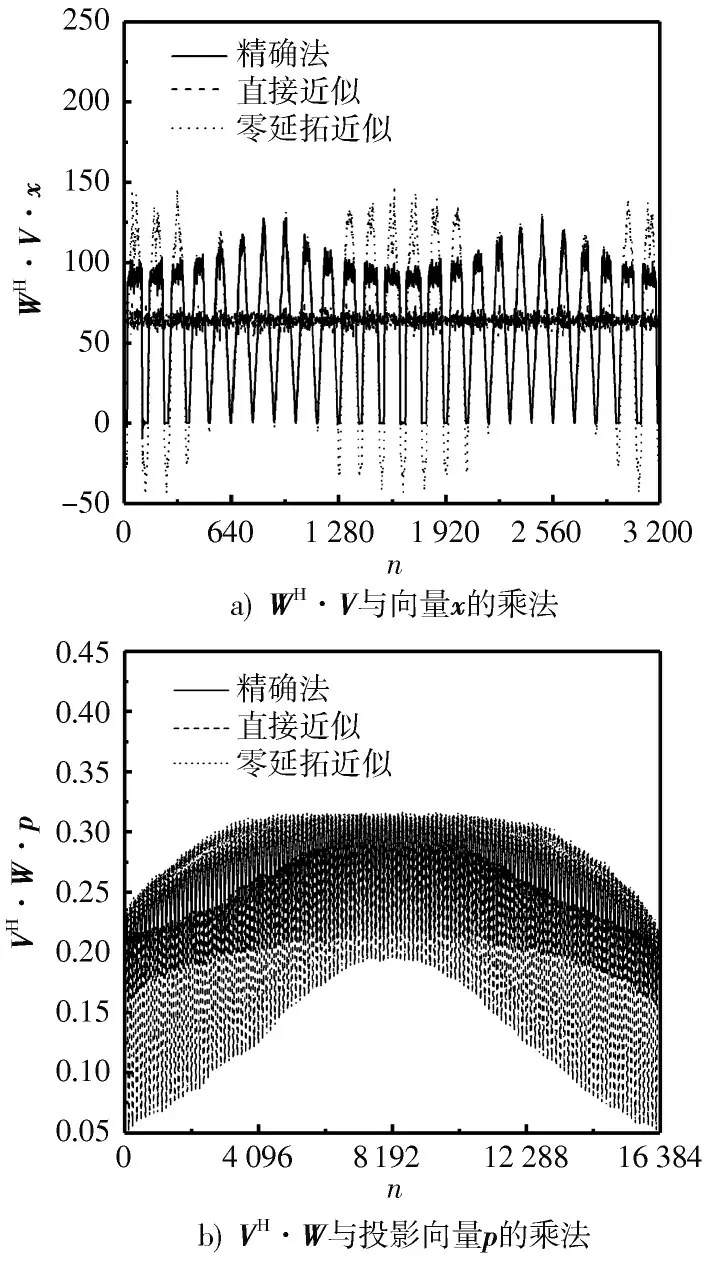
图6 精确解、直接近似和零延拓近似算法结果差异对比
内点算法在计算中需要多次计算矩阵向量乘法·和·,统计分析,对于不同维度场景成像,·和·的计算所消耗时间通常占据90%以上,如表1所示,因此重建算法的时间复杂性分析可通过对和的乘法进行分析。本文硬件平台采用AMD Ryzen 5,内存为8 GB。
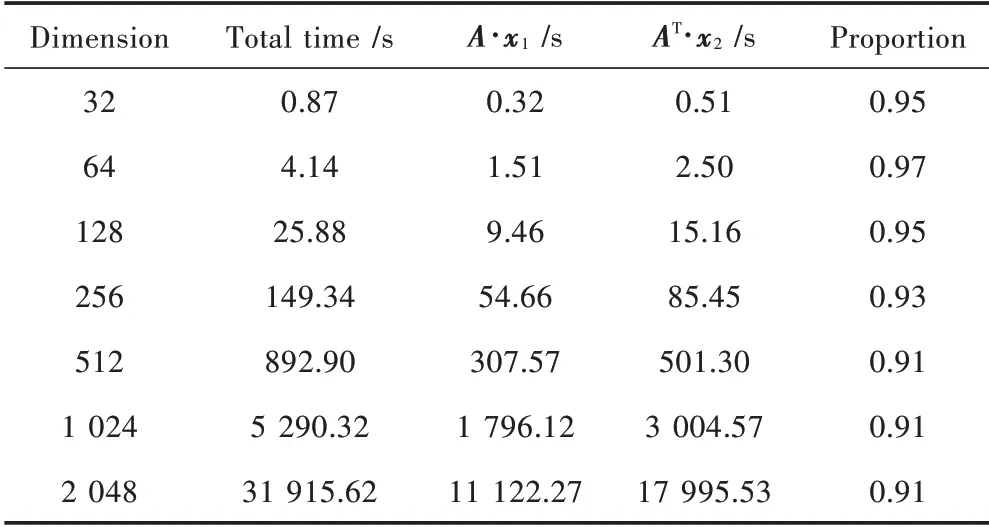
表1 零延拓近似算法的不同维度重建矩阵向量乘法运算时间占比
二维小波变换和2D⁃FFT 的算法复杂性均为(log),然而两者在矩阵乘法的时间消耗上通常占比小于10%,大部分消耗在矩阵元素的查找中(大于70%),其复杂性为()。因此图7 中,轴全部采用真实值的开方绘制。从图7a)中可看出,矩阵乘法的算法复杂性近似为(),与此同时,采用零延拓的方法计算量有少量增长,其中和的乘法分别大约增长1.5 倍和1.3 倍。图7b)为采用零延拓近似算法的成像总消耗时间曲线和内存消耗曲线,可以看出两者的增长趋势大于平方增长,最终在该硬件平台上实现了场景点数为2 048×2 048 的重建。
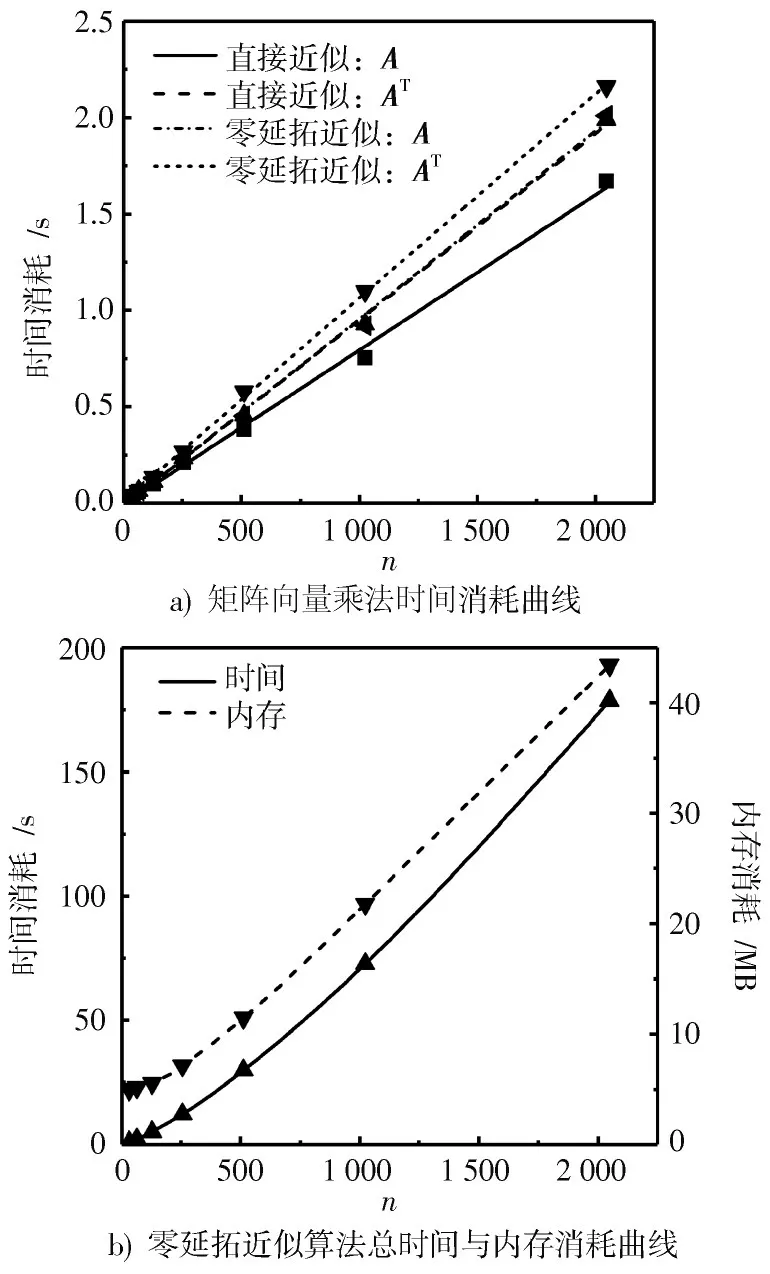
图7 零延拓近似算法性能分析
3 结 语
本文提出了一种基于CS的超宽带随机噪声SAR成像算法,该算法可以充分利用信号源的超宽带特性对场景高分辨率成像,它可以在欠奈圭斯特采样率下对信号进行采集处理,极大地减少了系统成本。考虑到大尺度场景成像的算法复杂性,本文提出零延拓近似算法,仿真结果表明,它在保持着较好精度的同时极大地降低了算法运算量。例如对点数为2 048×2 048 的场景重建,大约需要9 h,内存消耗约1.9 GB(普通PC 处理),而采用精确运算是无法实施的。
