一种基于神经网络的范围查找算法
2022-05-11彭永鑫
彭永鑫
(商洛学院数学与计算机应用学院,陕西商洛 726000)
近年来,高维度数据越来越广泛地应用于数据仓库[1]、信息检索和数据挖掘等领域。随着数据量不断增加,如何在海量数据中进行高效和有效地检索,查找到所需要的数据,成为人们日益关注的问题。范围查找是数据应用中经常使用的检索方式,即在一个数据空间中,给定一个查找对象,查询到与查找对象的距离小于等于查询半径的数据点[2]。作为范围查找的代表性方法,KD树和R树等树型结构查找结果虽然较为精确,但往往需要占用较大的存储空间,查找效率也较低。随着数据维度和数据量的增加,由于高维度向量的距离计算需要付出很大的代价,在查找的过程中会产生“维度灾难”[3],使得查找退化为线型扫描,极大影响查询效率。因此,有必要研究一种查找效率高,同时又不会损失过多查找精度的范围查找算法。
研究人员通常从改进查找过程及更快命中数据两个角度来提高范围查找的效率,例如Yesquel[4]、SLIK[5]和Nitro[6]。这些方法在一定程度上能降低维度和数据量的增加对查找效率带来的影响,但所能取得的效果有限。当前,随着数据量的日益积累,研究者开始探索更多的用于处理海量数据的方法。其中,使用机器学习模型替换现有模型的某个部分成为新兴的研究方向。Kraska等[7]明确提出了可学习索引(learned index)的结构。他们对如何使用机器学习模型代替B树进行了研究和讨论,并采用回归的方法,成功地将待查询点定位在一个最小误差值和一个最大误差值之间,验证了可学习索引模型在B树上的可行性。这种基于可学习索引模型的构建方法为解决空间数据查找问题提出了新思路。
可学习索引依托于神经网络模型,被证明是一种可行的用于代替某些索引结构的方法。传统的索引结构按照固定的方式组织数据,并不考虑数据的分布。而利用机器学习构建可学习的索引模型,在训练的过程中需要数据参与,能够在神经网络的不同层次中获得不同层级信息。许多传统索引结构的检索过程,可以看作是一个回归或者分类任务,这和神经网络能够完成的工作没有本质区别。因此,使用神经网络构建索引结构不但具有可行性,而且相比传统的索引结构可能会有更好的性能。在可学习索引的基础上,LISA[8]的提出使得查找任意空间数据集中的最近邻成为可能;ALEX[9]重点研究了查找策略的优化;Ali Hadian等[10]则讨论了数据更新对模型的影响。本文借助可学习索引模型和神经网络,提出一种新的范围查找算法,用于解决传统方法所面临的查找效率低等问题,并初步验证该算法的可行性。
1 树型结构的构建与范围查找
以二维平面为例(如图1(a)所示,其中P表示构成KD树的节点),对于一棵KD树,每个节点都会保存两个值,分别是所要分裂的维度和分裂的值。每个节点都会对二维空间的x轴或者y轴进行划分,将其余节点分割成两个部分,称为左子树和右子树,由矩形区域所组成。每一个由矩形构成的区域,称之为一个单元(由此产生的单元不一定有边界)。其中根节点对应的是整个空间。叶子结点存储位置信息,非叶子结点用于分裂,生成的KD树如图1(b)所示。

图1 二维平面KD树
使用KD树进行范围查找时,假设阴影部分(如图2(a)所示)为查找的区域R。查找过程如图2(b)所示。每次查找都从根节点开始。给定目前分裂的维度是x轴(或者y轴),左节点和右节点分别为l和r。如果节点l为一个叶子节点,返回这个节点所在单元和查找区域R相交的部分。如果这个叶子节点所在单元里的节点全都包含在查找区域R内,返回这个单元内的所有点;如果该单元不与区域R有交集,继续递归查询下一个节点。对右节点r也是相同的处理方式。
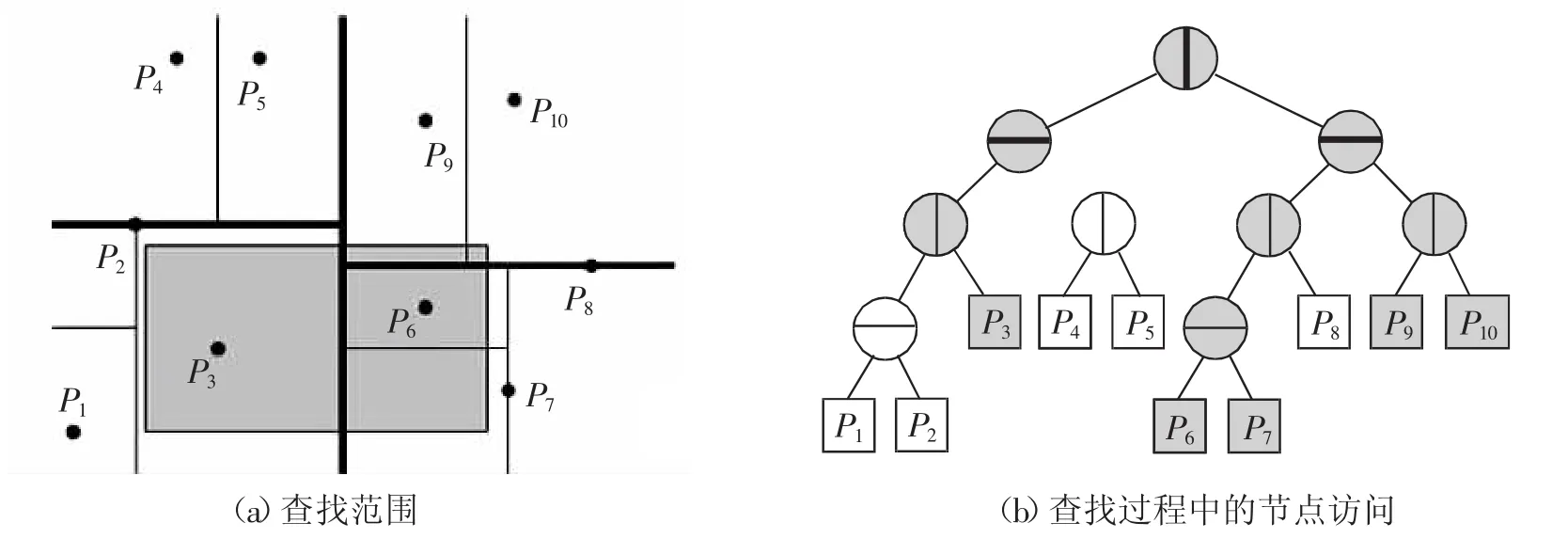
图2 KD树的范围查找
二维的情况下,使用KD树进行范围查找,最坏状态下的时间复杂度为tworst=O(n1/2+m)。其中,n是构成KD树的节点数量,即总的数据量的大小;m是输出数据的大小。将二维空间推广到d维,每次查找都会递归地分解到多个低维空间中去查找,容易得到其查找的时间复杂度是O((log n)d+md)。其中,md表示查找结果所组成集合的大小。其他用于范围查找的树形结构,例如R树,采用了空间分割的理念,其核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形,这个最小外接矩形就成为上一层的一个节点。因为所有节点都在它们的最小外接矩形中,所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。在此基础上,R*树[11]作为R树的一种变体,提升了R树的性能。使用KD树等树型结构进行范围查找在一定程度上能够满足多维查询功能,但会受到数据维度的制约。因此,需要对现有的算法进行改进或者提出新算法,使之能够满足更高的查询要求。
2 范围查找算法的构建与应用
使用神经网络代替范围查找算法,核心是使用训练好的神经网络模型进行运算,代替传统方法中的查找过程。使用KD树等树型结构进行范围查找,需要经过大量的回溯操作和距离计算才能得到精确的结果。基于神经网络的范围查找算法可以把这些回溯和计算过程用神经网络进行代替,同时辅以少量的计算和排序,在提高神经网络准确性的基础上,尽量得到相同或相似的结果。该算法首先需要确定查找对象q(x,y)、查找半径r和待查找区域R及数据点的总个数n。该算法要求所给定的待查找区域R里可能包含的最大数据点的个数不超过数据总个数n的a%,用数值k表示;区域R里包含的实际数据点的个数用k0表示。由此可知,k0总是小于等于k。
对于不同类型的索引结构,可以根据需要将其定义为回归或者分类任务。使用KD树进行范围查找,可以看作是一个多分类的问题,即待查询点和查找到的结果有着相似的属性,这种属性以距离的形式体现:距离越接近的,可以将其视作相似的分类。在构建可学习索引的过程中,使用监督学习的方式。在训练的时候,先构建好一棵KD树,并随机为这些构成KD树的每一条数据构建索引值,随后将训练集和测试集通过KD树得到k近邻点,将k近邻点转化为索引值,根据索引值得到训练集和测试集的标签进行训练。当模型训练好之后,待查询的数据点通过训练好的模型,输出多个可能是k近邻点位置的坐标,计算这些坐标和待查找点之间的距离并排序,取前k个值,从而得到真实的k近邻点。在神经网络训练的过程中,训练集为查找对象q的集合,标签为q的k个近邻点的坐标的索引值。准确率acc定义为神经网络所找到的k个近邻点占真实k近邻点的比值。由于区域R里所包含的实际数据点的个数k0总是小于等于区域内可能存在的最大数据点的个数k,所以在神经网络输出结果后还需要进行一次距离的计算,即计算神经网络输出的k个数据点和查找对象q的距离,将这个距离和查找半径r进行比较以排除查找区域外的数据点,继而得到区域R里的k0个数据点的坐标,就是满足范围查找要求的数据点。总体上讲,使用神经网络进行范围查找由两个部分组成,分别是索引部分和计算部分。索引部分通过神经网络得到查找对象q的k个近邻点的坐标,计算部分通过距离的比较得到最终的结果,即k0个数据点的坐标。因此,时间复杂度为O(1)+O(2),分别对应了索引部分和计算部分。在进行范围查找时,相对于KD树需要进行多次搜索计算和回溯操作,基于神经网络的范围查找只需要进行少量计算,从而节省了KD树在计算和回溯中所花费的大量时间。当构成KD树的数量和维度数变大时,此算法应该会表现出更明显的优势。
图3为使用神经网络的范围查找算法示例。其中整个区域内的数据点的总个数n为100,要求待查找区域R里可能包含的最大数据点的个数不超过数据总个数n的20%,即k为20。查找对象q(x,y)的坐标为(0.5,0.5),圆形区域为待查找区域R,查找半径为r,其中所包含的实际数据点的个数为k0,值为10,即为满足范围查找定义的数据点。索引部分得到的结果是矩形虚线区域内数据点的坐标,区域内数据点的个数为k,值为20,这些数据点是可能满足查找要求的数据点;在计算部分中,将矩形区域内数据点的坐标和查找对象q(x,y)进行距离的计算,距离小于r的数据点即为处在查找范围里的数据点,从而完成范围查找。
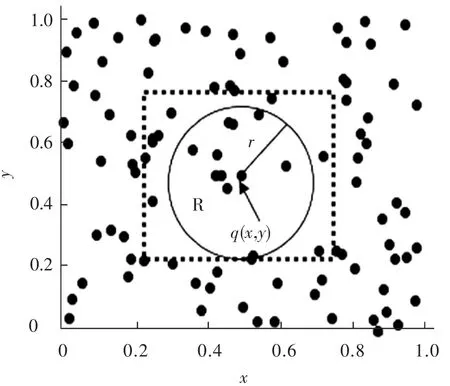
图3 基于神经网络的范围查找算法
算法的流程如图4所示。
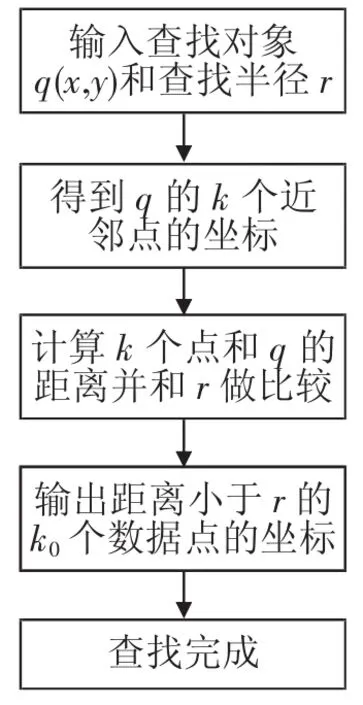
图4 范围查找的流程图
3 神经网络的构建
在神经网络训练的过程中,神经网络的层数并不是一个固定的值。对高维数据的范围查找来说,数据量n的大小决定了隐藏层数的多少。使用隐藏层,是为了对数据的特征进行提取。一般来说,隐藏层越多,提取到的特征就会越准确,整个神经网络的误差就会越低,使得精度会越高。然而,当隐藏层增加时,就会造成参数总量的增加,进而让神经网络的结构变得更加复杂,导致在神经网络的训练过程中更容易出现过拟合现象。同时,模型训练的时间也会增加。对此,可以采用增加隐藏层中节点数的方法,尽可能避免这个问题。相对于单纯地增加隐藏层的层数,增加隐藏层中节点数的方法更容易获得训练效果的提升。
因此,在基于神经网络的范围查找算法中,如何选择隐藏层的节点数成为关键。节点数目不但影响着模型的运行效率,而且当节点数量过多时,还会产生过拟合现象,从而影响查找结果。然而,现有的研究中,并未有被广泛用于确定隐藏层节点数的方法。由于不同的问题中训练样本各不相同,同时现在大部分方法中用于判断节点数的公式都是用于面对最不利的状况,这比较难以满足实际情况的需要。甚至由不同计算公式计算得出的节点数往往还会相差很大。本文中,为了使神经网络的性能得到一定程度的保证,同时保证模型的泛化能力,避免过拟合的发生,在保证准确率的基础上,尽可能使用较少的隐藏层节点数。在满足准确率的要求后,再对层数和节点数进行调整。由于隐藏层中节点数不仅与输入层和输出层的节点数有关,也和待处理数据的复杂程度有关,随着试验数据量的增加,层数和节点数也会随之增加。
4 结果与分析
在理论分析的基础上,通过试验来评估基于神经网络的范围查找算法的性能,与传统KD树的表现进行对比,并探索在何种情况下该算法更具优越性。判断的标准是查找时间和查找准确率,可以认为KD树的查找准确率为100%。查找时间指的是从查找对象q(x,y)和查找半径r输入到神经网络之后,再到最终查找到区域R内符合查找要求的k0个数据点所花费的时间。试验采用的数据集为生成的三维空间数据点所构成的五组数据集,分别满足均匀分布和正态分布。试验均使用python编写的代码在Intel(R)Core(TM)i7-4770上完成。深度学习框架则选用的是目前较为常见的TensorFlow,版本号为1.13。TensorFlow能便捷地对神经网络模型进行训练,而且能够将模型参数和模型结构进行固化后保存在特定类型的文件中方便后续的预测过程。
试验根据数据量n的不同分为五组,每组的数据量 n 分别为 1 000,10 000,100 000,200 000,500000。前三组数据满足均匀分布,后两组数据满足正态分布。神经网络由全连接层构成,每一层使用ReLU作为激活函数。层数和节点数随着数据量的增加而增加,分别为3层32个节点、3层64个节点、5层128个节点、6层64个节点和7层128个节点。学习率为0.000 1。为了排除偶然因素的干扰,每组试验的准确率acc和查找时间为10次试验结果的平均值。给定区域R里可能包含的最大数据点的个数不超过数据总个数n的1%。
表1展示了基于神经网络的范围查找算法的性能,并在同等条件下与KD树的表现进行了对比。从试验结果可以看出,当数据集满足均匀分布时,在n为1 000的情况下,使用基于神经网络的范围查找算法,准确率高达99.1%,但查找时间相比于传统的KD树要慢了很多,用时为1.05 s,耗费的时间超过KD树的2倍。当维度和数据量都比较小时,传统KD树由于搜索和回溯的次数较少,无疑能够表现出明显的优势;而基于神经网络的范围查找算法需要花费更多的时间在预测和距离计算上,导致查找时间增加。当n为10 000时,可以看到算法的查找准确率开始下降,为96.7%;但与之相对应的,算法所花费的查找时间和KD树在查找时间上的差距越来越小,耗费的时间为KD树的1.4倍。在维度不变的情况下,随着数据量的增加,KD树难以避免受到搜索次数增加的影响使其在查找效率上的优势逐渐缩小。当n为100 000时,算法的准确率略微降低到95.6%,然而在查找时间上已经表现出了一定的优势,其查找所需要的时间为1.41 s,而KD树用时为1.68 s。当数据集满足正态分布时,算法依然保持了较高的准确率,无论是200 000还是500 000条数据,准确率都在95%以上,而查找所用的时间分别为KD树用时的66%和60%,接近KD树查找时间的一半,表现出了较好的性能。可以预测到的是,随着数据量和维度的增加,有理由相信,基于神经网络的范围查找算法会表现出更强大的能力。
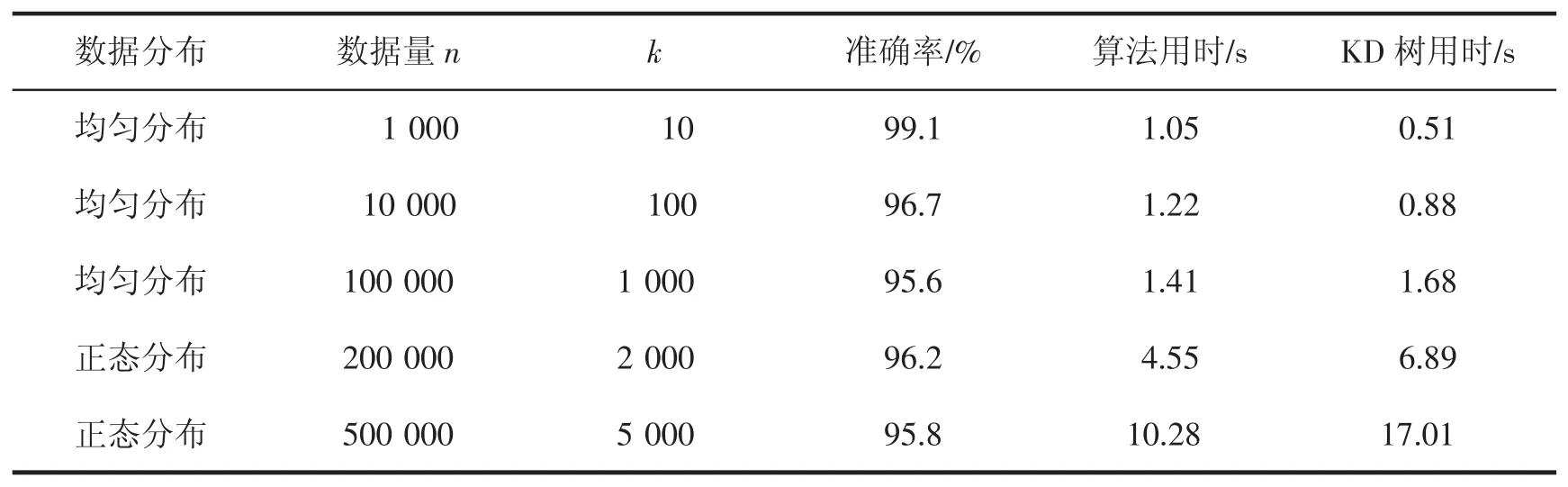
表1 基于神经网络的范围查找算法与KD树查找性能对比
5 结论
设计一种高效的范围查找算法是索引领域的研究热点。Kraska等[7]提出用可学习索引模型代替传统的B树,获得了引人注目的效果,为解决范围查找问题提供了新的方法和思路。本文在可学习索引的基础上,提出了一种用于解决空间范围查找问题的算法。该算法利用神经网络训练模型,当数据量较多时,在查找准确率较高,且查找时间上表现出优势的前提下,一定程度上解决了传统方法难以解决的由于数据量增加导致的查找效率下降的情况。该算法也存在一些不足,例如所取得的效果缺乏理论支撑,神经网络层数和节点数目的选择都是基于经验等。未来,将会从数学的角度出发,研究在更高维度和实际数据下该算法所能取得的效果。
