地震动加速度幅值对土坡失稳后滑坡体大小及致灾范围的影响*

张卫杰 余瑞华 宋 健 姬 建

(①河海大学岩土力学与堤坝工程教育部重点实验室，南京 210024，中国)(②河海大学江苏省岩土工程技术工程研究中心，南京 210024，中国)

0 引 言

滑坡是地震次生灾害中非常重要的一部分，其较远的滑动距离和较大的冲击力，给人民群众的生命、财产安全带来了巨大威胁，如触发滑坡最多的2008年汶川地震，有197 481处滑坡记录(许冲等，2019)，其中大光包滑坡面积达7.2 km2、体积约1.2×108m3，最大堆积厚度达550 m(黄润秋等，2014)；另一处红石沟滑坡最大水平距离达2700 m、最大高差920 m，估算滑坡体积为1.5×107m3(崔圣华等，2019)。可见，由地震引发的滑坡往往具有速度快、滑程远、冲击力大的特点(Bao et al.，2020a，2020b)，表现出大变形破坏的特征。从已有研究中分析可知，地震诱发滑坡的体积(Li et al.，2020)和位移(Rathje et al.，2011)是评估土坡抗震性能和滑坡灾害后果的重要指标。另外，滑坡体的致灾范围是判断滑坡能否对已有建构筑物造成损失及确定预警疏散范围的重要依据，因此对地震边坡破坏后的滑坡体大小和致灾范围进行研究具有重要意义。

地震作用下边坡的安全评价一直是岩土工程领域的研究热点之一(Hazari et al.，2020)。对于不同地震动力作用下的边坡稳定性问题，国内外学者的研究主要集中在：(1)不同地震动参数下边坡动力响应的规律(张江伟等，2017，2018；罗洋等，2019)；(2)不同地震动幅值作用下边坡的动力响应规律(Shamy et al.，2019；Song et al.，2019；韩雪等，2020)；(3)不同方向地震作用下边坡的动力响应(侯红娟等，2013)等。这些研究多数利用数值模拟或振动台试验研究不同地震作用下边坡的动力响应规律，但由于边坡大变形动力分析的困难性，地震边坡失稳后滑坡体大小和致灾范围研究依然少见。

近年来，越来越多的研究将弹塑性本构模型引入光滑粒子流体动力学(SPH)方法(胡嫚等，2019；Peng et al.，2019)，以更好地模拟土体在大变形状态下的应力-应变行为，揭示更为准确的土体大变形破坏规律。在地震边坡分析方面，Hiraoka et al.(2013)采用SPH方法模拟了边坡在地震作用下的动力响应；Bao et al.(2020a，2020b)提出了基于统一模型的SPH方法，模拟了地震滑坡的启动过程和滑动过程。尽管如此，地震边坡失稳后滑坡体大小和致灾范围方面的研究，特别是边坡坡角和地震动加速度幅值的影响规律研究，仍然存在不足。

本文基于SPH分析方法，采用基于Drucker-Prager破坏准则的弹塑性本构模型描述边坡土体的应力-应变行为，设置不同类型的粒子实现动力荷载的施加和自由场边界的模拟。利用SPH动力分析方法对已有文献中的振动台土坡试验进行了模拟，验证了该模型的准确性和精度。最后，通过对比4种坡度(30°、40°、50°及60°)土坡在不同地震动幅值作用下的SPH动力分析结果，揭示了坡角和地震动加速度幅值对边坡滑坡体大小和致灾范围的影响规律。

1 SPH动力分析方法原理

SPH的基本思想是将空间中连续的实体离散成一系列粒子，质量、速度、应力、变形等所有信息由这些粒子承载，粒子之间没有任何链接。在整个分析过程中，SPH方法需要追踪每个粒子在每个时刻的运动信息。其无网格性质及粒子间相互作用的特点使其更易处理大变形问题，消除了传统拉格朗日方法中网格畸变和扭曲等问题(Huang et al.，2014)。

SPH方法的核心问题包括光滑核函数的光滑近似和粒子近似。其中光滑近似可表示为如下的形式：

(1)

式中：W为光滑核函数；h为光滑长度；x为粒子的坐标信息。

函数及其导数的光滑粒子近似可以表示为：

(2)

(3)

式中：m为质量；ρ为密度；j为粒子指标。

本研究选择3次样条B函数作为光滑核函数(Huang et al.，2014)，其表达式为：

(4)

式中：R=|x-xj|/h，αd=15/(7πh3)。

SPH方法的控制方程包括连续性方程、动量守恒方程和能量守恒方程。在不考虑滑坡体温度变化的情况下，可以忽略能量守恒方程，只考虑连续性方程和动量守恒方程。根据质量守恒定律，连续方程的SPH形式如下，

(5)

式中：Wij为土粒子j在土粒子i处的光滑核函数值；v为速度；m表示方向；i和j为粒子指标。为了获得更加稳定的密度计算，可以对式(5)进行正则化修正，得到：

(6)

另一个控制方程是动量方程，由牛顿第二定律推导得出，如下所示：

(7)

式中：σ是土粒子的应力张量；m、n是坐标方向指标；δmn是狄拉克函数；人工黏度项Πij被用来防止粒子的非物理穿透，其计算方法在文献(Zhang et al.，2016)中列出。

土体的应力-应变行为需要通过具体的本构模型进行描述，在本研究中采用基于Drucker-Prager破坏准则的弹塑性本构模型描述边坡土体的应力-应变行为。具有非关联流动规则的基于Drucker-Prager破坏准则的弹塑性本构模型在Bui et al.(2007，2013)和McDougall et al.(2005)的工作中有详细介绍，根据他们的工作，该模型的增量形式为：

(8)

式中：λe和μe是拉梅常量，可以通过弹性模量E和泊松比υ计算得到；dεij是总应变增量，其他组成部分的计算方法如下：

(9)

(10)

C=λefkkgll+2μefklgkl+gkk

(11)

f是可以在Bui et al.(2007)的工作中找到的屈服函数：

(12)

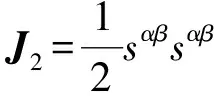
(13)

g是塑性势函数：

(14)

式中：ψ是剪胀角；常量αψ由下式计算：

(15)

如果摩擦角φ和剪胀角ψ不同，为非联合流动法则。如果摩擦角φ和剪胀角ψ相同，则是联合流动法则。由以上可知，fij和gij可按下式计算：

(16)

(17)

研究方法中，边界是由若干层虚拟粒子组成的，与运动粒子(土粒子)具有不同的粒子类型。在处理边界的过程中，假设边界粒子具有一个虚拟速度，能够用于运动粒子速度梯度的加权平均。边界粒子对运动粒子的影响是根据两者之间的相对距离来确定的。在地震动荷载施加方面，通过对底部固定边界粒子施加速度，从而在粒子层面上实现了动力荷载的施加。本研究底部采用Hiraoka et al.(2013)的具有地震荷载的无滑移边界，来实现动力荷载的施加；具体可描述为:

VAB=VA-VB=β(VA-Vseismic)

(18)

VB=(1-β)VA+βVseismic

(19)

式中：VA、VB和Vseismic分别为土粒子速度、边界粒子速度和地震波速度。其中：β=min(βmax，1+dB/dA)，是与运动粒子和边界粒子之间距离有关的参数。

基于Bao et al.(2020a)的研究，本文在左右边界处设置自由场边界粒子，以减少地震波的反射。在数值模拟中，自由场粒子被迫移动，通过边坡粒子和自由场粒子在地震和重力作用下的同步计算，将自由场粒子的不平衡力施加于边坡粒子的横向边界，使得计算区域中真实粒子产生的向外波被适当地吸收，以满足横向边界上的位移和应力条件，从而实现自由场边界的粒子化建模。

2 SPH动力分析方法的验证

为了验证本文SPH动力分析方法在地震土坡模拟上的准确性，本研究将其应用在黄栋等(2017)的土坡振动台试验模拟中，通过对比地震边坡的最终变形形态来验证本文方法的有效性。该土坡的尺寸如图1所示。计算模型中粒子总数目为6977，其中边界粒子有2118个，土坡土粒子有4857个，粒子初始间距为0.01 m。左边界设置为自由场边界，在荷载作用下发生运动，计算区域内运动粒子产生的向外波被适当地吸收以减少地震波的反射。初始状态下，土坡粒子静止不动，计算开始后可以在重力作用下运动。在初始的计算步中，利用弹性模型对土坡的自重应力进行初始化，此后在地震动施加过程中，采用弹塑性模型描述土体的应力-应变行为。SPH模拟的单位时间步长为2.5×10-5s，计算总步数为1.21×107步，故稳定分析的总时间为302.5 s，其中模型自重平衡的时间设置为1 s，地震动施加时间为300 s。另外，在地震动施加完毕之后，边坡模型仍然具有速度，需要1.5 s的时间让边坡恢复静止状态。SPH中使用的具体计算参数可见表1，本构模型参数如表2所示。

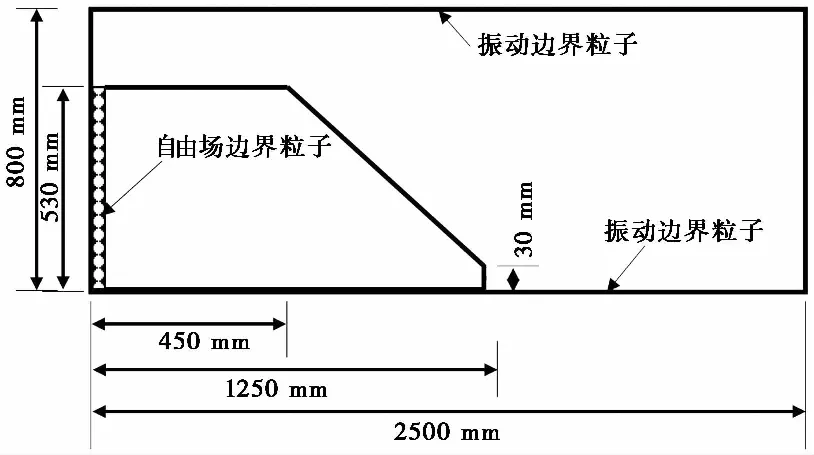
图1 振动台土坡模拟尺寸图

表1 振动台土坡模型SPH模拟的参数

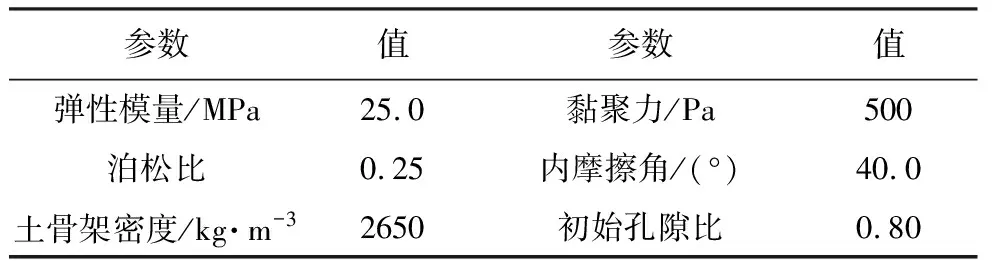
表2 振动台土坡模型SPH模拟中的本构参数

本案例施加的地震波与黄栋等(2017)论文中振动台施加的地震波相同，即分别按照100 Gal(2 Hz、5 Hz、10 Hz)，300 Gal(2 Hz、5 Hz、10 Hz)，500 Gal(2 Hz、5 Hz、10 Hz)，700 Gal(10 Hz)逐级加大加速度和频率进行激励。每级振动时间为30 s，每级振动荷载施加完毕后暂停一段时间。

图2展示了输入地震波强度为 500～700 Gal 时SPH模拟得到的土坡变形破坏形态。黄栋等(2017)将振动台土坡变形破坏过程分为4个阶段：(1)土坡振动固结和前缘堆积阶段；(2)裂缝扩展贯通阶段；(3)整体滑动阶段；(4)堆积体稳定阶段。本文利用SPH动力分析方法得到的土坡破坏呈现出与黄栋等(2017)类似的变形破坏过程，如图2所示。土坡在运行至地震波500 Gal 2 Hz施加完毕(即844万步)时，土坡有明显粒子滑落，于土坡前缘堆积；在地震波500 Gal 5 Hz施加完毕(即964万步)时，土坡出现贯穿坡顶至坡脚的滑动面；在地震波500 Gal 10 Hz施加完毕(即1084万步)时，土坡继续滑动，但滑动距离不大；在地震波700 Gal 10 Hz施加完毕(即1204万步)时，土坡的滑动区域明显增大。图3展示了SPH数值模拟的最终破坏形态与振动台试验的最终破坏形态对比，两者最终坡形基本吻合，且土体的最大滑动距离在数值上非常接近。由此可见，本文中提出的SPH动力分析方法在地震土坡变形分析上具有较高的精度和准确性。

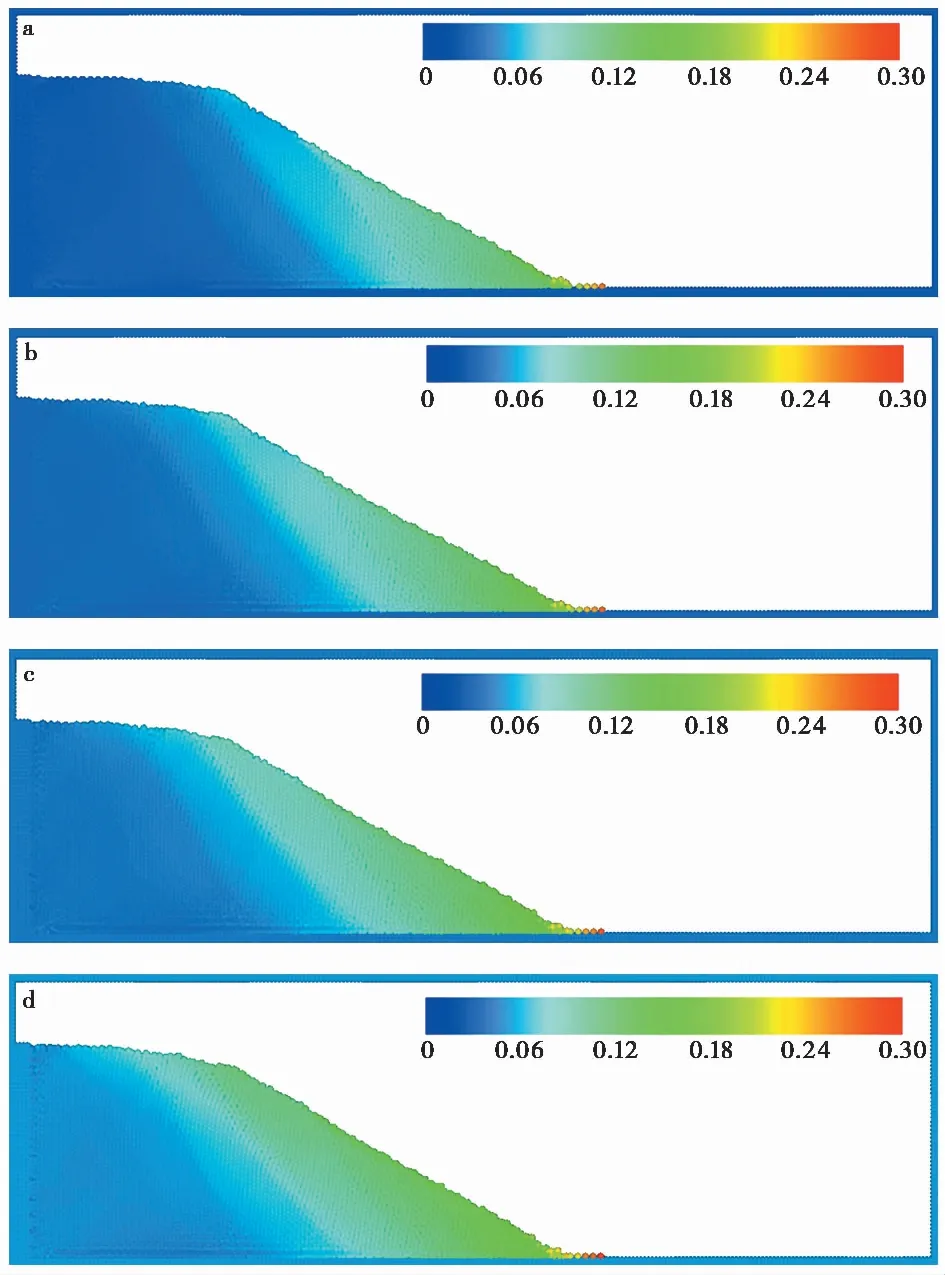
图2 SPH模拟的试验土坡变形发展过程图(单位：m)

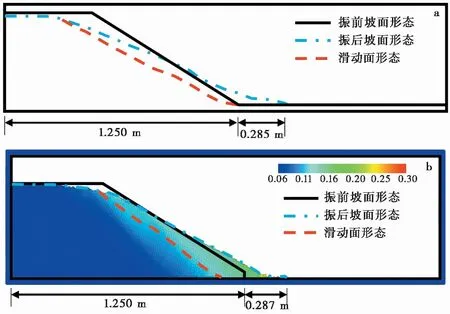
图3 土坡最终形态对比图(单位：m)

另外，本研究中在自由场边界外设置了振动边界(图1)，从振动台试验边坡的模拟结果来看，左侧振动边界粒子对边坡动力响应的影响很微小，证明了本研究振动边界及自由场边界设置的可行性。

3 不同地震动加速度幅值的影响分析

3.1 模拟案例

为了分析不同坡度土坡在不同地震动加速度幅值作用下的滑坡体大小和致灾范围，研究建立了4种坡度的计算模型，分别是30°、40°、50°及60°。具体的尺寸如图4所示，振动边界粒子与自由场边界粒子的设置也展示在图4中。

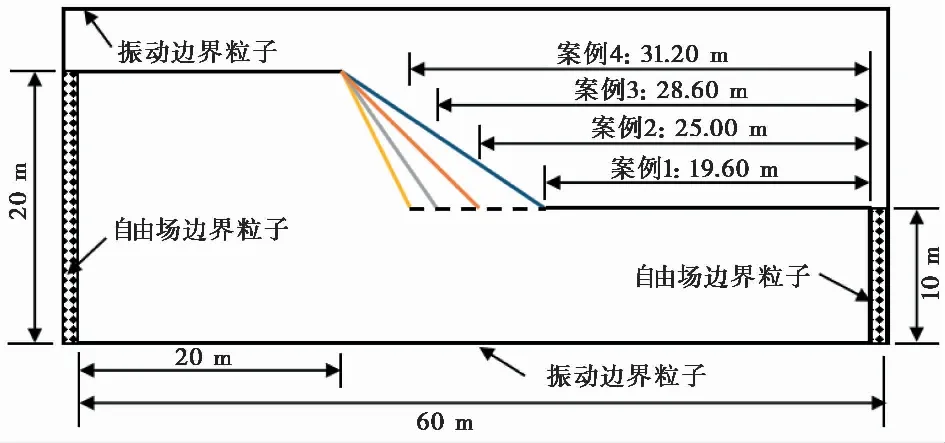
图4 不同土坡尺寸图

计算模型的粒子总数目随土坡坡度而改变，粒子初始间距统一设置为0.20 m。在初始状态下，土坡粒子静止不动，计算开始后可以在重力作用及地震作用下运动。同样地，在初始的计算步中，利用弹性模型对土坡的自重应力进行初始化，此后在地震动施加的过程中，采用弹塑性模型描述土体的应力-应变行为。SPH模拟的单位时间步长为5.0×10-5s，计算总步数为6.4×105步，分析的总时间是32 s，其中地震动施加时间为30 s。SPH中使用的具体计算参数见表3，本构模型参数如表4所示。

表3 土坡模型SPH模拟的参数

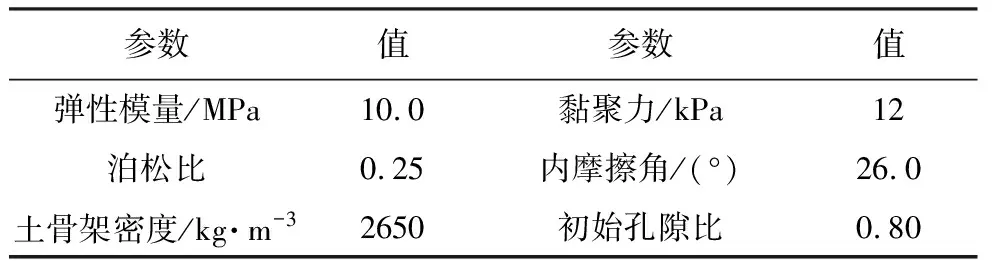
表4 土坡模型SPH模拟中的本构模型参数

本文的数值模拟首先需要在重力作用下实现初始地应力平衡，因此要求重力作用下的边坡是稳定的，即安全系数≥1.0。若边坡在自重应力作用下的安全系数<1.0，自重应力下边坡无法保持稳定，后续就无法考察地震动作用对边坡稳定及失稳滑动的影响。另外，本研究通过FLAC2D计算得到的各边坡安全系数均>1.0。

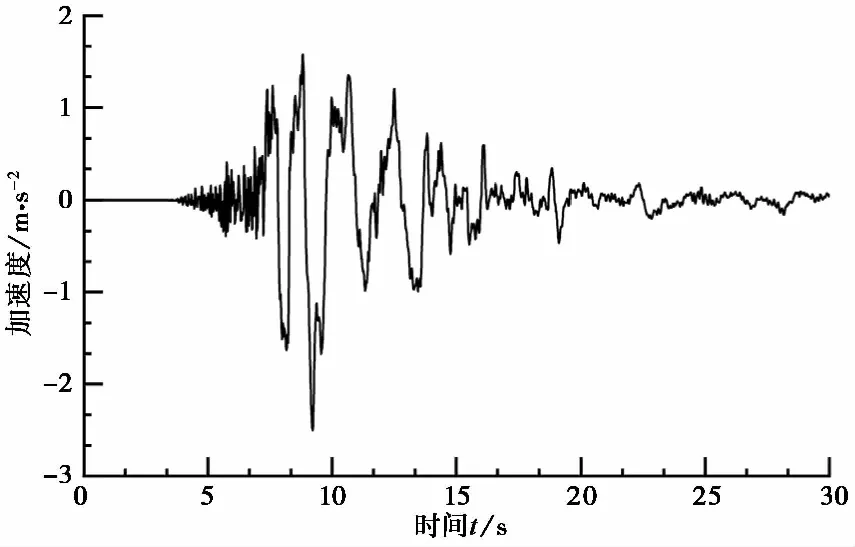
图5 KOBE波加速度时程图

本案例一共模拟了12个工况，具体设置如表5所示。基于OpenMP并行计算框架，在配备双路Intel Xeon E5,2520V4处理器、64 GB DDR4内存和Ubuntu Linux 20.04操作系统的工作站上设置了16线程，每个工况消耗时间约100 min。

表5 SPH模拟土坡工况表

3.2 结果分析

由于篇幅限制，这里选定40°和60°土坡在不同地震动幅值作用下的总位移云图进行比较，分别如图6和图7所示。可以看出，在同一比例尺下，40°土坡在1.0倍地震动加速度幅值作用下只在坡顶处有较小变形；而在地震动幅值2.0倍和3.0倍作用下土坡整体有较大变形，出现了清晰且连续的位移较大区域，代表着该区域可能发生滑动，即滑坡体的范围，其面积可以用来衡量土坡失稳后滑坡体的大小。60°土坡在1.0倍地震动加速度幅值作用下就出现了明显的位移较大区域，表示出现了可能的滑坡体。另外，同一土坡在不同地震动幅值作用下存在相似的滑动面，且其潜在的滑动区域随着地震动幅值的增大而增加。从图例中也可以明显地看出，60°土坡存在更大的位移峰值。由此可知，对于具有相同参数的土坡，坡度越大稳定性越差。

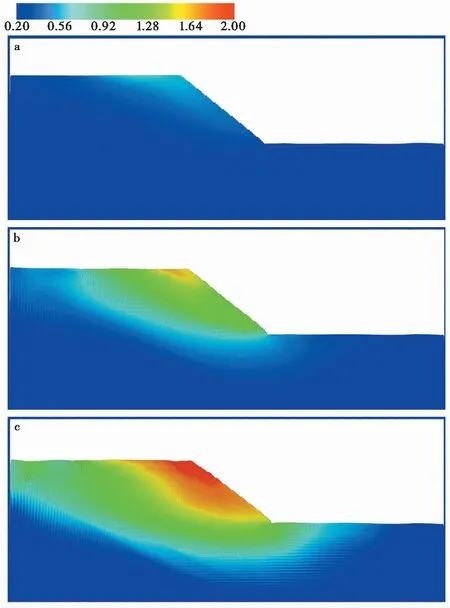
图6 边坡角为40°的土坡在不同地震动幅值作用下的总位移云图(单位：m)

图7 边坡角为60°的土坡在不同地震动幅值作用下的总位移云图(单位：m)

取土坡各工况下滑坡体区域的最大水平位移值作为地震土坡的滑动距离，可以表征地震土坡失稳后的致灾范围。图8所示的是土坡在不同地震动幅值作用下最大水平位移的变化柱状图。可见，随着土坡坡度增大，不同地震动幅值作用下土坡的最大水平位移均呈非线性增加趋势。

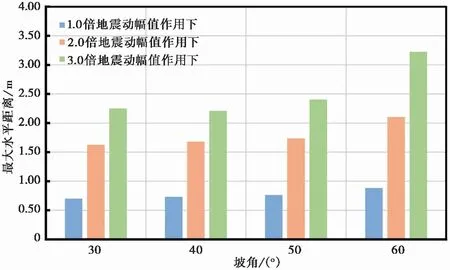
图8 不同地震动幅值作用下土坡最大水平位移变化柱状图

目前常用剪应变来确定土坡的潜在滑移面，Li et al.(2020)验证了利用位移阈值确定土坡滑动面的准确性。结合本案例，比较了40°和60°土坡在2.0倍地震动幅值作用下由剪应变和总位移确定的潜在滑动面，如图9所示。可见，最大剪应变确定的土坡潜在滑动面与总位移确定的潜在滑动面具有一定的吻合度，滑动面均通过坡脚，且两者界定的滑体大小也较为相近。因此，利用位移阈值确定土坡滑动面的方法具有一定的准确性。

图9所示的坡体在边界处有些异常。原因是自由场粒子在吸收了地震波后产生速度和位移，其位移与土体位移存在微小差异。边坡边界处的异常与边坡剪应变和位移相比较为微小，对模拟结果的影响也较微小。这在振动台试验边坡的模拟结果中得到了体现。

图9 在2.0倍地震动幅值作用下40°和60°土坡剪应变和总位移云图(单位：m)

结合本案例土坡选取的参数及土坡的最大总位移值，研究选取了不同的位移阈值来确定土坡的滑动面。之后，通过将总位移云图简化，得到了更为清晰的滑坡体分布图，进而为计算各土坡的滑坡体大小(以滑动区域的面积代替)提供了便利。由于1.0倍地震动幅值作用下各土坡的位移值较小，未出现较为清晰的滑动面，这里只计算和展示了2.0倍和3.0倍地震动幅值作用下的数据结果。图10是以0.60 m为位移阈值的各土坡在2.0倍地震动幅值作用下的滑坡体分布图。图11是以0.60 m为位移阈值的各土坡在3.0倍地震动幅值作用下的滑坡体分布图。

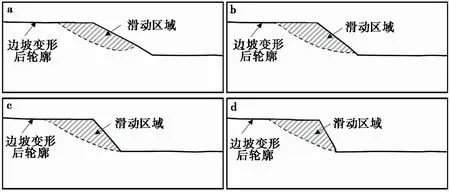
图10 以0.60 m为位移阈值各土坡在2.0倍地震动幅值作用下滑坡体分布图

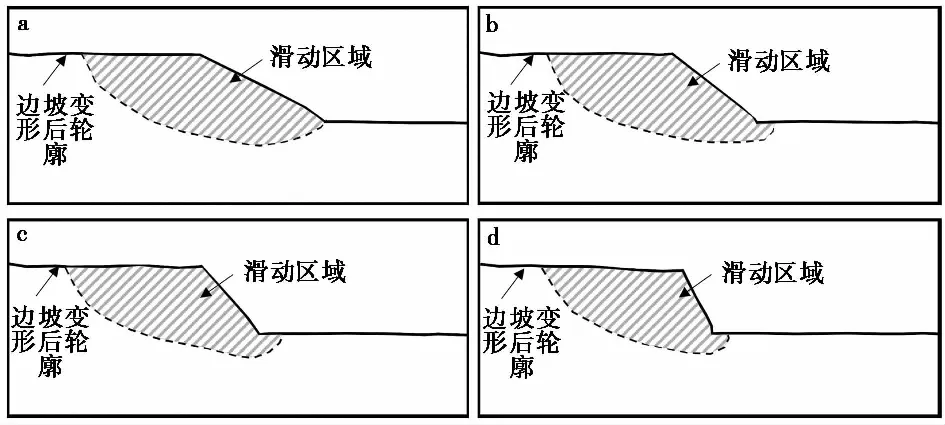
图11 以0.60 m为位移阈值各土坡在3.0倍地震动幅值作用下滑坡体分布图

通过观察滑坡体分布图，可知，土坡的滑坡体大小与土坡坡度并不是简单增加的关系，甚至土坡坡度越大，其滑体区域可能会越小。之后通过具体计算土坡在不同位移阈值之下的滑坡体区域，得到了具体的滑坡体数据，由此绘出了如图12和图13所示的土坡在2.0倍地震动幅值作用和3.0倍地震动幅值作用下的滑坡体大小随坡度变化曲线。可见，同一位移阈值下各土坡滑坡体大小随坡度的增大近似线性减小，且2.0倍地震动幅值作用和3.0倍地震动幅值作用下的各土坡滑坡体大小的变化规律相同。

图12 2.0倍地震动幅值作用下不同位移阈值土坡滑坡体大小变化曲线

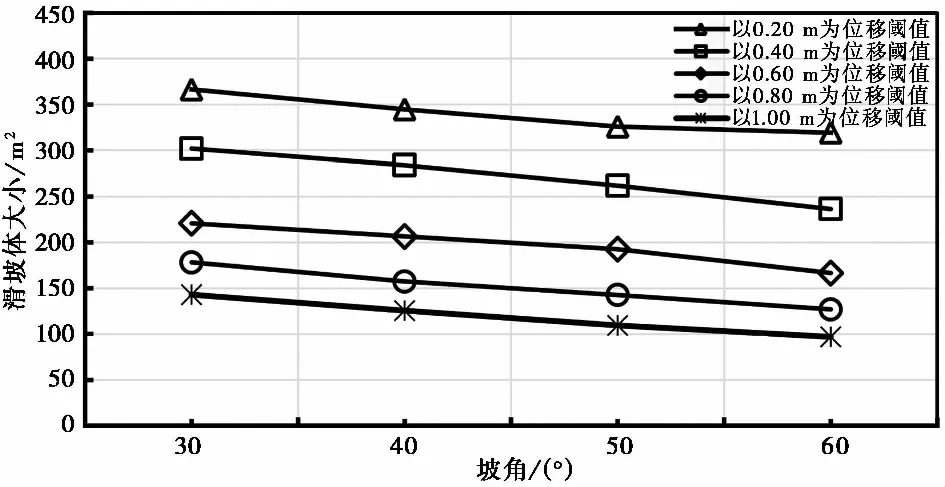
图13 3.0倍地震动幅值作用下不同位移阈值土坡滑坡体大小变化曲线

综上所述，随坡度的增加，各土坡在地震作用下的稳定性下降，致灾范围变大；但滑坡体的区域面积会减小。

4 结 论

本文基于SPH动力分析方法，采用基于Drucker-Prager破坏准则的弹塑性本构模型作为土体的弹塑性本构模型，设置不同类型的粒子实现了动力荷载的施加和自由场边界的模拟。利用SPH动力分析方法对已有文献中的土坡破坏振动台试验进行了模拟，对比两者的最终形态，验证了该模型的准确性和精度。通过对比4种坡度土坡在不同地震动幅值作用下的SPH动力分析结果，揭示了坡度和地震动加速度幅值对地震土坡滑坡体大小和致灾范围的影响规律。本研究得到的主要研究结论可归纳如下：

(1)本文利用SPH动力分析方法对已有土坡破坏振动台试验进行了模拟，得到了与试验类似的破坏过程、基本吻合的坡形、及数值上非常接近的最大滑动距离，验证了SPH动力分析方法在地震土坡变形分析中的精度和准确性。

(2)通过对比同一坡度土坡在不同地震动加速度幅值作用下的SPH模拟结果，可知同一土坡在不同地震动幅值作用下存在相似的滑动面，且潜在滑动区域随着地震动幅值的增大而增加。

(3)通过对比不同坡度土坡在地震动作用下相应位移阈值确定的土潜在滑动面与最大剪应变确定的潜在滑动面，证实了利用位移阈值确定土坡滑动面的方法具有一定的准确性。

(4)通过对比不同坡度土坡在同一地震动加速度幅值作用下的SPH模拟结果，可知随坡度的增加，各土坡在地震作用下的稳定性下降，致灾范围变大；但滑坡体的区域面积会减小。