基于PSO-MLSSVR的土体参数反演方法在深基坑工程中的应用*

程秋实 杨志双 秦胜伍 张领帅 苗 强 张延庆

(吉林大学建设工程学院，长春 130026，中国)

0 引 言

随着我国经济快速发展，城市建设日益增多导致所能利用空间逐渐减少。建造高层建筑成为一种解决城市用地不足的有效方法，相应的深基坑工程也越来越多(李庄伟，2015)。由于城市建设用地资源日益紧张，拟建的建筑物周边环境日益复杂，毗邻大量的建筑物、地下管线、地下设施等，所以研究基坑施工过程对支护结构和周边环境的影响具有工程实际意义，可以提前预测和减少后期潜在的损失(陈文玲等，2014；豆红强等，2018；李冕，2020；秦胜伍等，2020；胡瑞庚等，2020；周勇等，2021)。

深基坑变形预测是进行施工过程调整和确保深基坑施工安全的重要手段，而对基坑变形进行有效、准确的预测是一个有待解决的技术难题(刘贺等，2014；施有志等，2018)。如今被广泛应用于基坑施工变形预测的方法是数值模拟，它在岩土工程开挖、加固以及防护设计等方面有着优异的表现，而影响数值模拟预测结果的最大问题是如何准确确定岩土体的计算参数(孙超等，2019)。基坑的施工是一个动态过程，施工期间土体受到降排水、开挖、变形等因素的影响，土层的参数会产生非线性变化，将岩土力学参数看成固定不变的值去分析一个动态的施工过程，预测结果将达不到预期效果(陈浩冲，2017)。因此根据施工过程反分析土体参数的方法逐渐发展成为获取土体计算参数的主流手段之一，其中基于位移的反分析方法在工程中得到广泛应用(孙钱程等，2019)。葛增杰等(2000)将人工神经网络方法应用于深基坑开挖工程中多层土体物性参数的识别问题。杨杰等(2006)提出基于最大熵原理的贝叶斯不确定性反分析方法，将信息熵理论与贝叶斯法有机结合，通过适当的优化求解方法，实现对坝体和坝基材料参数反演分析。朱海琴等(2017)利用遗传算法、BP神经网络、正交试验设计和有限元数值方法相结合，对软基土体参数进行反演和工后沉降预测。郭子奇等(2020)构建了PSO-BP神经网络对地铁盾构场地土体参数进行反演修正，建立的神经网络反演结构反映了地表沉降与土体参数之间的非线性关系。在过去的几年中，引入了支持向量回归机(support vector regression，SVR)，它在小样本集，非线性和高维的情况下具有更好的性能(Bao et al.，2020)。Su et al.(2016)采用人工神经网络(Artificial Neural Networks，ANN)和SVR在混凝土坝弹性模量反分析中选择最优资源。Liu et al.(2017)应用无约束拉格朗日SVR来估计高拱坝的弹性模量。卢远富等(2019)提出了利用在线支持向量回归和ABAQUS反演坝体与坝基力学参数的方法，其中ABAQUS作为正算位移场的求解器被反复调用，在线支持向量回归模型用于建立测点位移与待反演参数间非线性映射关系。

现阶段在边坡和隧道领域，参数反演方法已经被广泛应用，但是相比之下对于较复杂的深基坑的参数反演研究较少。这是由于深基坑的支护结构复杂，传统的计算方法对深基坑的土体参数进行反演难度较大。随着机器学习技术的发展，机器学习开始广泛应用于岩土参数反演研究中，为深基坑的参数反分析提供了一个新的思路(Luo，2018；Mao，2019)。肖明清等(2017)提出一个基于BP神经网络的动态施工反演分析方法，利用参数敏感性分析和BP神经网络的动态施工反演分析方法建立土体与基坑位移的非线性关系。沙勇华等(2017)提出了PSO-SVM算法与有限元联合反演模型，建立起土体力学参数与桩顶竖向位移之间的高度非线性映射关系。

本文使用一种粒子群算法(Particle Swarm Optimization，PSO)结合多输出最小二乘支持向量回归机(Multioutput Least-Squares Support Vector Regression Machine，MLSSVR)的位移反分析法。该方法可以克服支持向量机模型中参数选择的主观性以及利用单输出支持向量机建立多测点模型时计算量大、精度较低等缺点。首先设计正交试验方案，将设计的参数进行有限元计算获得训练样本，之后通过MLSSVR建立反演土体参数与多个位移点之间的映射关系，并使用粒子群算法搜索MLSSVR的模型参数，寻找与实际位移最拟合的岩土参数，使用反演的土体参数进行有限元计算得出测点的计算位移，最后与工程实际监测值进行对比分析。本文将PSO-MLSSVR位移反分析法应用于实际工程案例中，为基坑工程数值模拟的土体参数选取提供一种新方法。

1 PSO-MLSSVR土体参数反演方法

1.1 MLSSVR

对于给定的训练集(X，Y)={(x1，y1)，(x2，y2)，…，(xl，yl)}，xi∈Rn为输入向量，yi∈Rm为输出向量，MLSSVR将n维输入xi∈Rn映射到m维输出yi∈Rm，构造了一个回归函数(Xu et al.，2013；Zhu et al.，2018)：

f(x)=φ(x)TW+bT

(1)

式中：φ(x)表示非线性映射函数;W=(w1，w2，…，wm)，wi表示特征空间的权向量;b=(b1，b2…，bm)，bi表示偏置量。

确定相应的最小化问题的目标函数和约束条件前，需定义repmat(A，m，n)或repmat(a，m，n)是一个由A或a组成的m×n平铺的块状矩阵，此外，blockdiag(A1，A2，…，An)或blockdiag(a1，a2，…，an)是一个分块对角矩阵，其主要对角块为A1，A2，…，An或a1，a2，…，an。

相应的最小化问题的目标函数和约束条件如下：

s.tY=ZTW+repmat(bT，l，1)+Ξ

(2)

权向量wi可以分解为以下两部分：

wi=w0+vi

(3)

式中：w0为均值向量；vi为差分向量；w0和vi分别反映了输出结果之间的关系和差别。

式(2)的最小化问题等同于以下问题：

s.tY=ZTW+repmat(bT，l，1)+Ξ

(4)

式中：V=(v1，v2，…，vm)。

定义的拉格朗日函数如下：

L(w0，V，b，Ξ，A)=J(w0，V，Ξ)-

trace(AT(ZTW+repmat(bT，l，1)+Ξ-Y))

(5)

式中：A=(α1，α2，…，αm)是由拉格朗日乘数的向量组成的矩阵。

根据Karush-Kuhn-Tucker的优化理论条件：

(6)

式中：el=(1，1，…，1)T。

去掉式(6)中的W和Ξ后，可以得到以下线性矩阵方程：

(7)

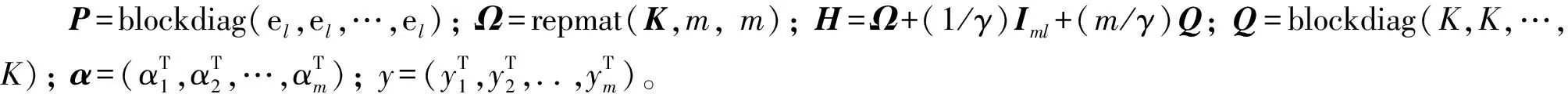
可以得到相应的回归函数如下：

f(x)=φ(x)TW*+b*T

(8)

K(x，xj)为MLSSVR的核函数，本文采用了最常用的径向基核函数(RBF)，它适用于提取样本的局部特征，而且具有较强的插值能力，RBF公式如下：

(9)

式中：σ为内核宽度。

1.2 PSO

PSO算法是由许多随机解在空间中搜寻，然后通过不断地迭代来找寻群体的最优解的优化算法(李爱国，2002)。在粒子群算法中，空间中的粒子就是每一个优化函数的解都被初始化为随机粒子群，每个解的粒子都有其适应度值，这个适应度值则由目标函数来确定。在粒子群算法不断迭代的过程中，有两个极值的存在，一个是个体极值Pbest，另一个是全局极值gbest。个体极值是所有粒子在全部迭代过程中的最优值，全局极值是随着迭代过程不断更新的值，也就是粒子群体的最优值。

群体中第i个粒子在n维空间的位置表示为x=[x1，x2，…，xi]，其速度为ν=[ν1，ν2，…，νi]，第i个粒子的个体极值为Pbest=[Pi1，Pi2，…，Pin]，整个粒子群全局极值gbest=[gi1，gi2，…，gin]。在算法每次迭代时搜索出上述两个极值后，通过如下式(10)来将粒子变动位置：

(10)

式中：k为迭代次数；c1、c2为学习因子；rand1和rand2是(0，1)之间的随机数；ω是惯性权重。本文为了克服PSO算法容易陷入局部最优，无法获取全局最优近似解，本文引入简单变异算子，在粒子每次更新之后，以一定概率重新初始化粒子。

1.3 MLSSVR的学习样本及测试样本构建

在实现MLSSVR的学习过程之前，需要准备初始训练集 {(x1，y1)，(x2，y2)，…，(xl，yl)}和测试输入x0。在本文训练集中，输出向量yi为土体参数的组合，输入向量xi为使用土体参数进行有限元计算的测点的水平位移，x0为工程现场监测的测点水平位移。首先需要根据实验结果和工程经验确定土体参数取值范围，然后在范围内选择不同的力学参数值进行组合。这一过程如果使用穷举法设计组合土体参数，组合的数量将太多，导致使用有限元方法计算会消耗过长时间，对于实际工程并不适用。本文采用正交设计方法选择几个有代表性的土体参数组合，而不是采用所有可能的组合。

根据岩土勘察报告和工程经验，基坑开挖主要影响土层为填石层，淤泥层和砂质黏土层。在深基坑支护结构位移和土体参数选取的研究中(吴才德等，2017；庞小朝等，2018；张亚西，2019；刘蓉，2020；阮永芬等，2020)，发现修正莫尔-库仑模型中的割线模量E50获取较困难且模量参数对基坑开挖变形的影响较大，在工程中E50一般取弹性模量的倍数，所以本文选择填石层，淤泥层和砂质黏土层的割线模量E50为待反演参数，并根据工程经验确定了E50取值范围，如表1所示。

表1 模型土层参数取值

本文采用正交试验设计有限元计算方案来得到不同岩土参数组合下支护结构顶部水平位移监测点的各工况的水平位移值，通过正交设计方法将前3个工况各自设计了25组实验，反演参数的数量为3，每个参数的水平为5，设计的表格如表2所示。在给定各因素水平下，25次实验可以有效确定相应规律，我们按试验号进行有限元计算，计算监测点的位移。

表2 正交试验设计表

1.4 研究流程

基于正交试验设计和PSO-MLSSVR的岩土力学位移反分析技术路线图如图1所示，具体流程如下：

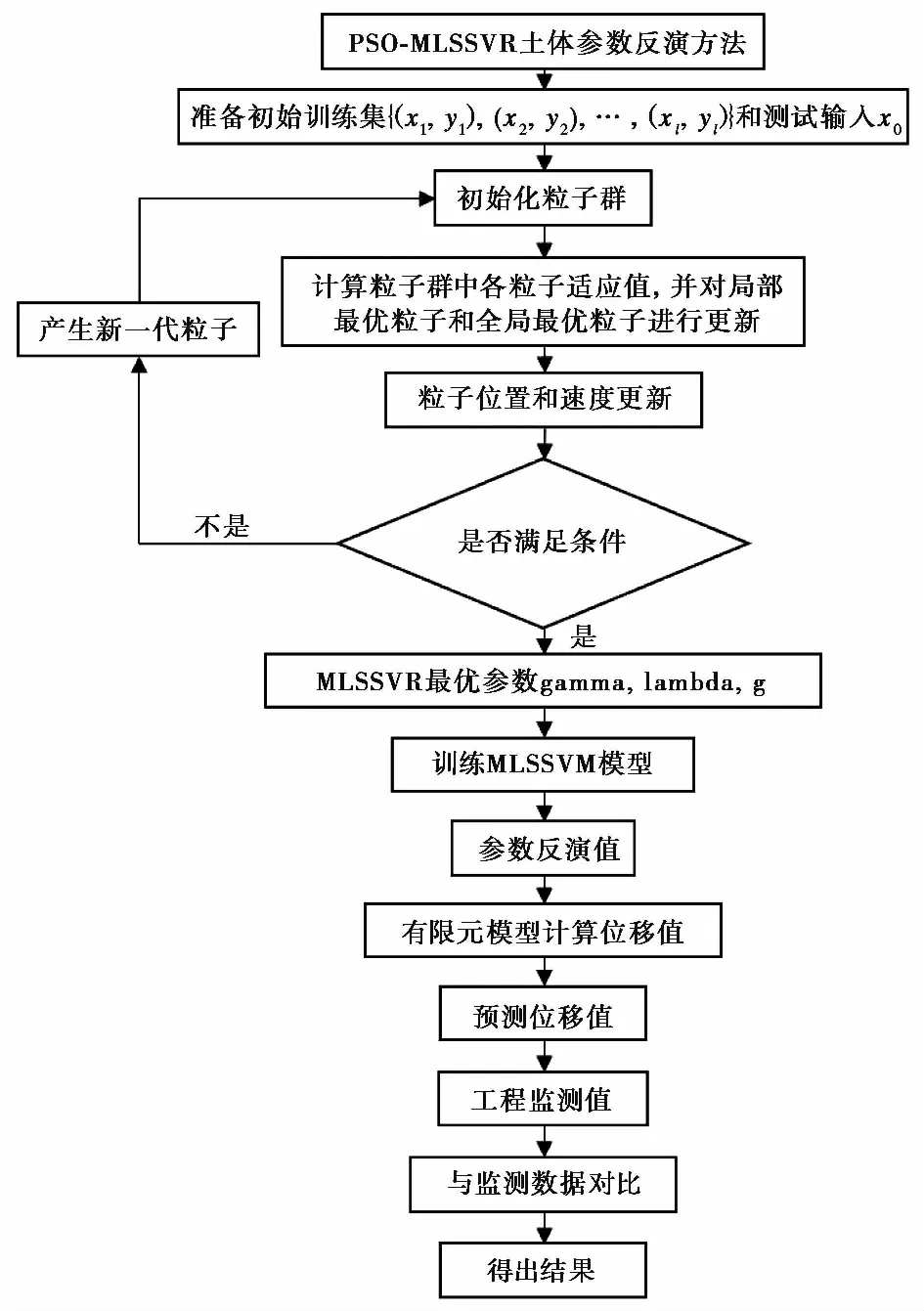
图1 技术路线图

(1)根据工程资料和经验，确定待反演参数的取值范围，利用正交设计构造计算方案。

(2)将每次正交设计的试验数据依次输入到有限元软件中作正分析，得到初始训练集 {(x1，y1)，(x2，y2)，…，(xl，yl)}，数据需要归一化到[0，1]的范围内，以消除数量级和尺寸的影响。

(3)对粒子群算法进行设置，每个粒子向量对应MLSSVR的参数γ、λ和g。代入MLSSVR进行训练并得到相应的参数预测值，将预测结果的均方误差(MSE)作为粒子的适应值，优化MLSSVR模型参数。本文适应度值是交叉验证的均方误差，将训练集分成10份，轮流将其中9份作为训练数据，1份作为测试数据，对每个MLSSVR模型进行训练和测试，得到MSE的平均值，适应度值具体公式如下：

(11)

(4)将粒子群算法搜索到的最佳参数代入MLSSVR模型，建立待反演参数与位移之间的非线性映射关系，将测试样本代入MLSSVR模型中得到反演参数，将反演参数代入到有限元模型中进行计算，并将结果进行对比验证。

2 实际案例

2.1 工程概况

拟建项目场地位于深圳市前海自贸合作区，地下拟建4层地下车库。场地呈现不规则方形，总用地面积约为1.2×104m2。场地地面标高为9.0 m，支护长度约为435 m，支护深度约为19.00～21.00 m，场地东侧目前为空地，距离梦海大道约为20 m，南侧为规划市政地块和其他项目地块，西侧为规划市政地段，距离100 m为地铁一号线(罗宝线)，北侧约为20 m为桂湾二路。场地所在区域原始地貌单元属海岸阶地，经填海改造，目前场地整体地势较为平坦，高程7.63～6.02 m，相对高差为1.61 m，研究选定的支护结构顶部水平位移监测点(J1、J2、J3、J4、J5、J6、J7、J8)分布和基坑具体位置信息如图2所示。

图2 基坑平面图及监测点布置

场地地层自上而下可分为第四系地层，未分统的残积层，白垩系上统地层、侏罗系地层。场地的中上部为第四系土层含孔隙水，下部基岩含裂隙水。场地地下水位埋深为1.70～2.60 m，标高5.33～3.72 m。考虑到基坑周围邻近道路，侧壁为较厚软土层，根据不良地质条件及周围环境采用灌注桩+桩间双管旋喷桩+三道钢筋混凝土内支撑的支护方案，灌注桩采用Φ1400 mm@1700 mm钻孔灌注桩，灌注桩间采用Φ800 mm双管旋喷桩作为止水帷幕，内支撑采用1000 mm×1200 mm和1200 mm×1200 mm的钢筋混凝土梁系统。竖向方向三道支撑布置深度为3.5 m、9.7 m、15.5 m，立柱上侧采用Φ600 mm钢管立柱，坑底下侧为Φ1000 mm钻孔桩，支护结构的剖面图如图3所示。

图3 支护结构剖面图

2.2 模型建立

本文选用MIDAS-GTX有限元软件进行模拟分析，本构模型的选择对数值模拟结果的精确程度有很大影响(胡建林，2021)。本文选择修正莫尔-库仑模型，修正莫尔-库仑模型是一种弹塑性模型，能够有效反应土体的变形过程，该模型比莫尔-库仑模型更加适用于各种类型地基的模拟(徐中华，2010；李连祥，2016)。边界条件为底部设置水平和竖直方向约束，4个侧面设置法向方向约束。考虑边界对模拟结果的影响，根据基坑开挖影响范围经验值及查阅相关文献(宋辰辰，2019；赵涛等，2021)，选取模型水平方向影响范围为开挖深度的3倍，纵向影响范围为开挖深度的2倍。根据基坑大小和开挖深度，确定的模型大小为327 m×312 m×63 m，其中基坑尺寸为117 m×112 m×21 m。为了便于计算，模型将非连续的钻孔灌注桩等价为连续性的板桩墙结构，基坑采用Φ1400 mm@1700 mm的钻孔灌注桩，根据两者刚度等价的原则可得(胡斌等，2014)：

(12)

式中：D为钻孔灌注桩间距；h为等效的地下连续墙宽度；d为钻孔灌注桩直径。

由于受施工空间限制基坑共分为4次开挖，开挖深度分别为4.3 m、10.5 m、15.3 m、21 m，待每层土开挖完成后施工钢筋混凝土内支撑，详细的模拟施工工况如表3所示。

表3 模拟施工工况

内支撑和钢管立柱采用梁单元模拟，围护桩使用板单元进行建模。模型使用混合网格生成器进行网格的建立，共创建125 798个网格，91 908个节点建立模型如图4所示。根据地勘报告和相关文献(施有志，2016；张丽芬等，2019)，模型土体参数的选取如表4所示。

表4 模型土层参数取值

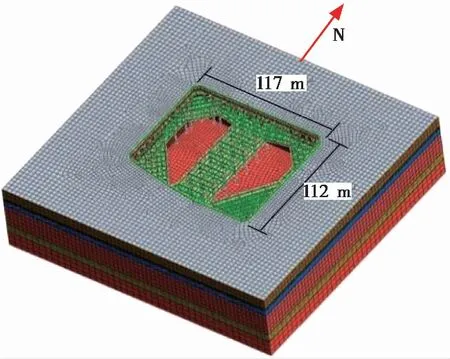
图4 有限元模型图

3 结果分析

3.1 正交实验设计样本集

训练集按照正交试验设计出每个工况25组训练样本，将测点的监测值作为测试输入，训练样本和测试输入如表5所示，序号1～25为训练集，26为测试输入。

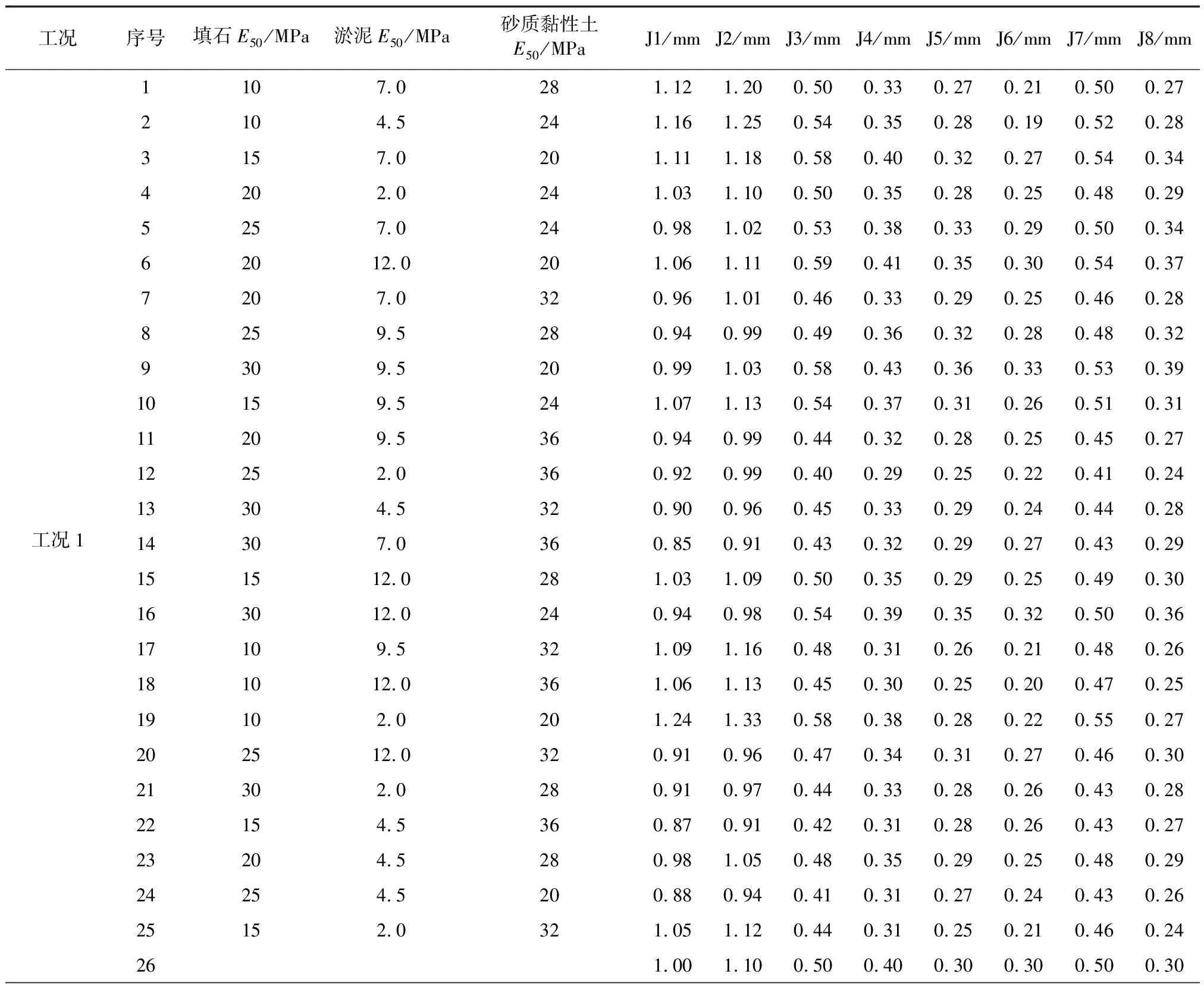
表5 正交设计学习样本

3.2 MLSSVR与LSSVR反演结果对比分析

多输出最小二乘支持向量回归机(MLSSVR)是最小二乘支持向量回归机(LSSVR)在多输出情况下的推广。本文通过PSO算法对MLSSVR和LSSVR进行参数寻优，随后建立模型进行土体参数反演，对单输出与多输出结果进行对比分析，表6为工况3情况下两种方法得到的反演参数，得到有限元计算结果如图5所示。从图5的J1、J2、J6和J7这4个测点的图像可以明显看出，MLSSVR得到的反演参数有限元计算结果比LSSVR结果拟合得更好。

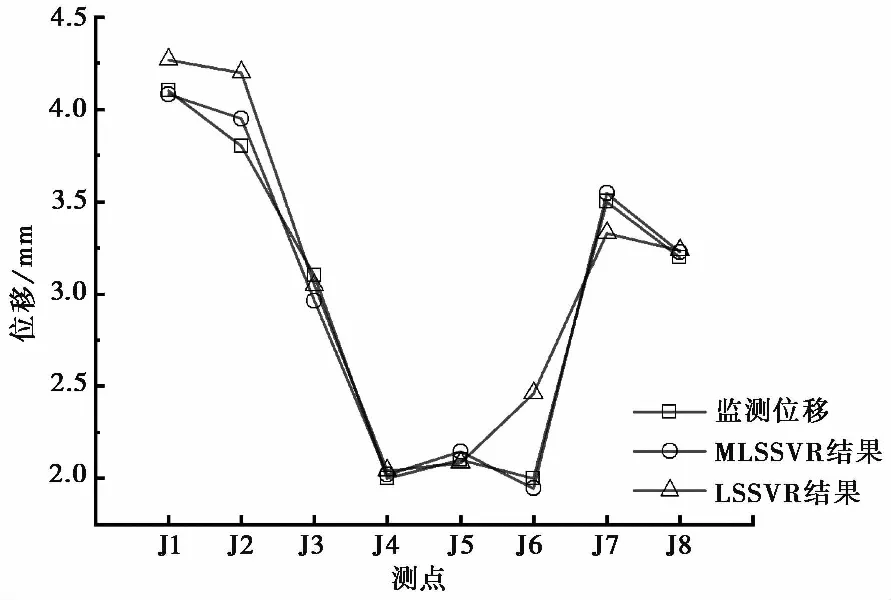
图5 工况3有限元计算值与监测值对比图

表6 工况3土体参数反演值

表7为两种方法得出结果对比表，从表中可以看出平均绝对误差、最大绝对误差、平均相对误差、最大相对误差和总CPU时间。从表7中可得出MLSSVR得出结果的相对误差更小且运算时间更短，证明使用MLSSVR进行土体参数反演时精度和效率上都优于单输出LSSVR。虽然LSSVR的泛化性能较好，但是LSSVR应对多输出情况时，大多是通过训练多个独立的LSSVR模型来实现，这样就忽略了不同参数之间潜在的非线性交叉相关性，而MLSSVR可只建立一个模型应对多输出情况，且MLSSVR模型中可以同时考虑所有的土体参数，这可以反映不同参数之间的联系，所以MLSSVR反演过程耗时较短同时精度较高。

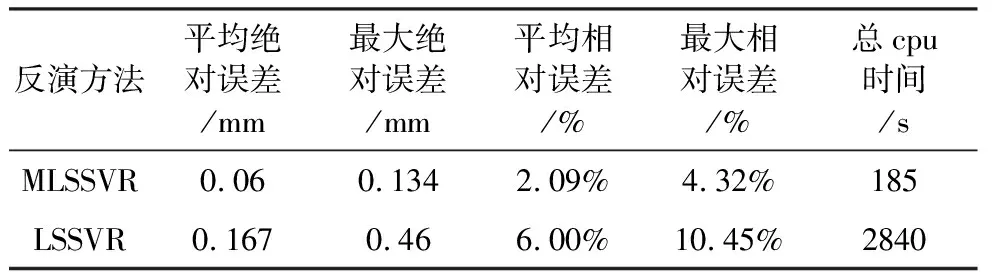
表7 工况3反演验证结果

3.3 反演结果分析

应用PSO搜索MLSSVR最优模型参数γbest、λbest和gbest，参数k取200，c1取1.5，c2取1.7，ω取0.5。最终的结果如表8所示。

表8 MLSSVR模型参数

将得到的最优模型参数代入MLSSVR模型进行训练并进行测试，利用MLSSVR模型建立反演参数与位移之间的映射关系，对填石层、淤泥层和砂质黏土层的E50进行土体参数寻优，MLSSVR模型获得的土层参数如表9所示。

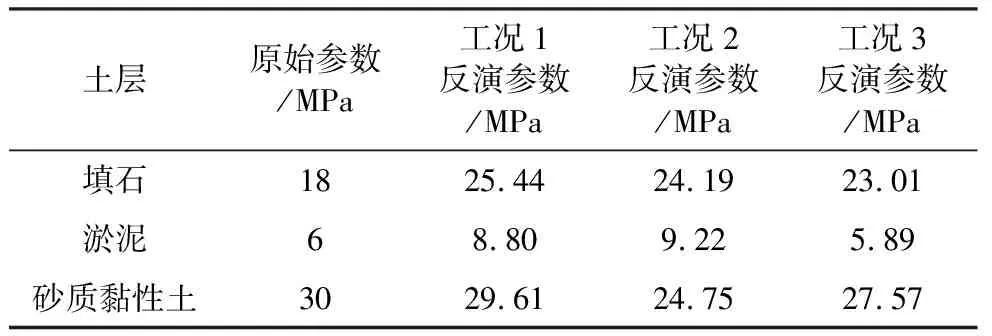
表9 土体参数反演值

将反演的土体参数代入有限元模型后，得到J1～J8监测点的模拟结果，并与监测数据进行对比，如表10所示。从表10中可以看出，使用工况1反演参数进行有限元计算，最大相对误差为18%，平均相对误差为8.03%，工况2最大相对误差为8.9%，平均相对误差为3.44%，工况3最大相对误差为4.32%，平均相对误差为2.09%，反演结果有限元计算值与实际监测值接近。相对误差是绝对误差与监测值之比。相对误差随基坑开挖的进行而变小，是由于受有限元软件精度的限制，水平位移数据值较小时，有限元计算得到位移值与监测值相比有微小不同，相对误差也会很大，随着开挖的进行，水平位移增大，有限元计算结果的位移值有微小的误差也不会对相对误差产生较大的影响，相对误差会逐渐减小且最终趋于稳定。

表10 反演验证结果

同时考虑岩土参数是动态的，将反演的土体参数代入有限元模型计算下一工况的位移值，其计算位移与实际监测位移的对比见图6。从图6中可以看出，反演参数有限元计算的位移比原始参数计算的位移更加贴近实际监测值，验证了反演参数方法的准确性与实用性。

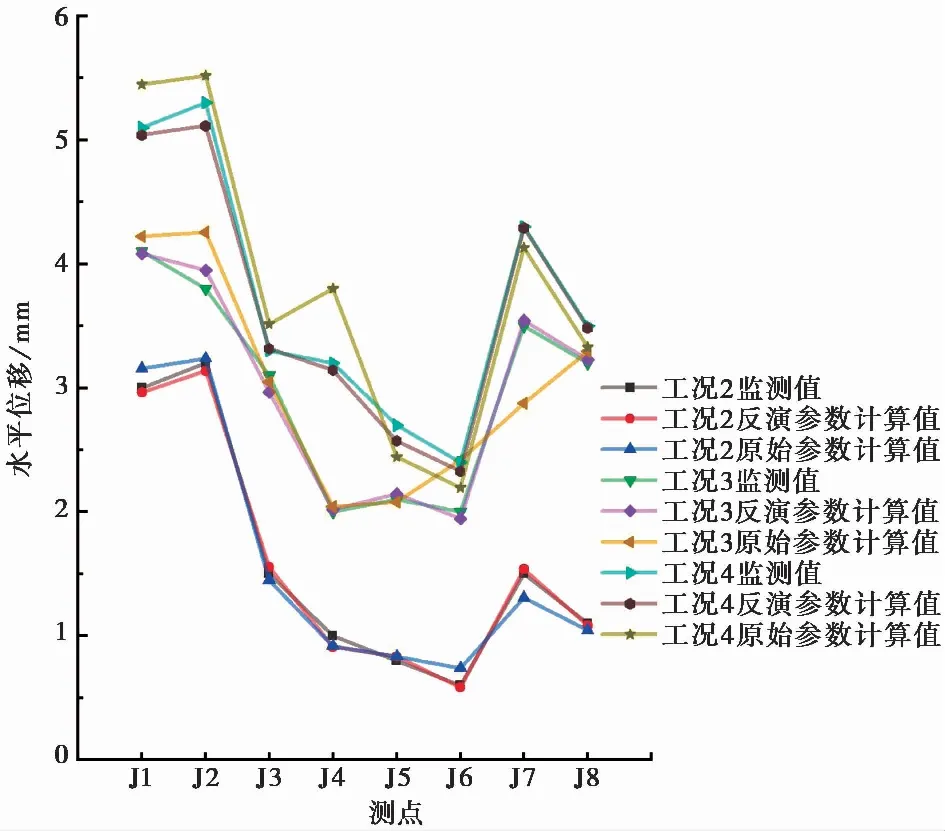
图6 有限元计算值与监测值对比

4 结 论

本文以深圳市某深基坑为例，使用PSO-MLSSVR反演填石层、淤泥层和砂质黏土层的土体参数，并将反演参数有限元计算结果与原始参数和PSO-LSSVR得到参数的有限元计算结果进行比较，得出结论如下：

(1)本文以深圳某深基坑为例，使用PSO-MLSSVR和PSO-LSSVR进行土体参数反演，MLSSVR克服了LSSVR建立多测点模型时计算量大、精度不高的缺点，结果证明使用MLSSVR进行土体参数反演的精度和效率比单输出的LSSVR更好。

(2)将MLSSVR得到的反演参数代入有限元模型中计算测点位移值，得到的结果与监测数据非常接近，工况1最大相对误差为18%，平均相对误差为8.03%，工况2最大相对误差为8.9%，平均相对误差为3.44%，工况3最大相对误差为4.32%，平均相对误差为2.09%，结果表明基于PSO-MLSSVR的位移反分析法具有较高的精度，证明通过基坑顶部的监测数据来反演基坑的刚度模量，可获得较为精准的土体参数。

(3)本文考虑土体参数随开挖阶段发生变化，将反演的土体参数代入有限元模型中计算下一工况的位移，其计算位移比原始参数计算位移更加贴近实际监测位移，证明研究方法可满足实际工程中分阶段分析的需求。