基于改进遗传神经网络的地表沉降预测★

孙 瑞，张 波，张文胜，桑学文，王 辉

(1.北京市轨道交通设计研究院有限公司，北京 100068； 2.石家庄铁道大学交通运输学院，河北 石家庄 050043)

地表沉降是影响隧道施工安全的重要因素[1]，威胁到施工人员的安全，可能造成严重的后果[2]，准确的预测地表沉降具有重要的意义。国内许多学者对沉降预测方法进行了研究，目前预测沉降的方法有经验分析法、概率积分法、数值模拟法、时间序列分析法、人工神经网络法等[3-5]。赵紫龙[6]利用基于小波分解的差分灰色神经网络——AR模型对隧道沉降进行了预测，并证明了预测的准确性；李翔宇等[7]基于上海地铁实测数据，利用粒子群算法对BP神经网络进行了优化，运算速度快且预测精度佳；张士勇等[8]利用深度学习小波神经网络模型对地表沉降预测，得出该模型比传统小波神经网络和BP神经网络模型精度高的结论。

BP神经网络是一种多层前馈神经网络，应用非常广泛。单独使用BP神经网络模型预测地表沉降时，容易陷入局部极值[9-12]。将神经网络与其他算法结合起来，往往能得到更好的效果。将改进后的遗传算法与BP神经网络相结合，以克服神经网络的缺陷，使地表沉降预测结果更准确。

1 遗传算法选择算子

遗传算法模拟生物进化论的自然选择机制，具有多个遗传算子，通过遗传算子可以从种群中选拔出优秀的个体，使有较强适应能力的个体更有可能成为下一代的父代。选择算子是一个关键的遗传算子[13-16]。

2 遗传算法选择算子的改进

提出了“等级选择法”，在锦标赛法的基础上，将种群中的个体按照适应度进行排序，然后分成四个等级。进行下一代选择操作时，为四个等级的个体分配特定的比率。这样不仅确保在种群中选择更好的个体，而且可以在不破坏全局的情况下保持种群选择的多样性。等级选择法过程如下。

Step 1初始种群oldPop列数为Pb+1，行数为种群内个体数量N。

Step 2按适应度值递增顺序，将种群内个体排序，得到centerPop。

Step 3按适应度值大小，排好序的个体分为差、中、良、优四级，选择概率分别为P0,P0+δ,P0+2δ,P0+3δ，选择出来的个体数量分别为ncha=N/4×P0,nzhong=N/4×(P0+δ),nliang=N/4×(P0+2δ),nyou=N/4×(P0+3δ)，此时，候补个体数为nhoubu=N-nyou-nliang-nzhong-ncha。

Step 4确定好四个等级以及候补等级个体数后，对不同等级个体进行选择。对于候补个体，优先从优级选择，若优级不够，则从良级选择。

Step 5将优、良、中、差四级个体和候补个体进行拼接，得到新种群newPop。

等级选择法的步骤如图1所示。

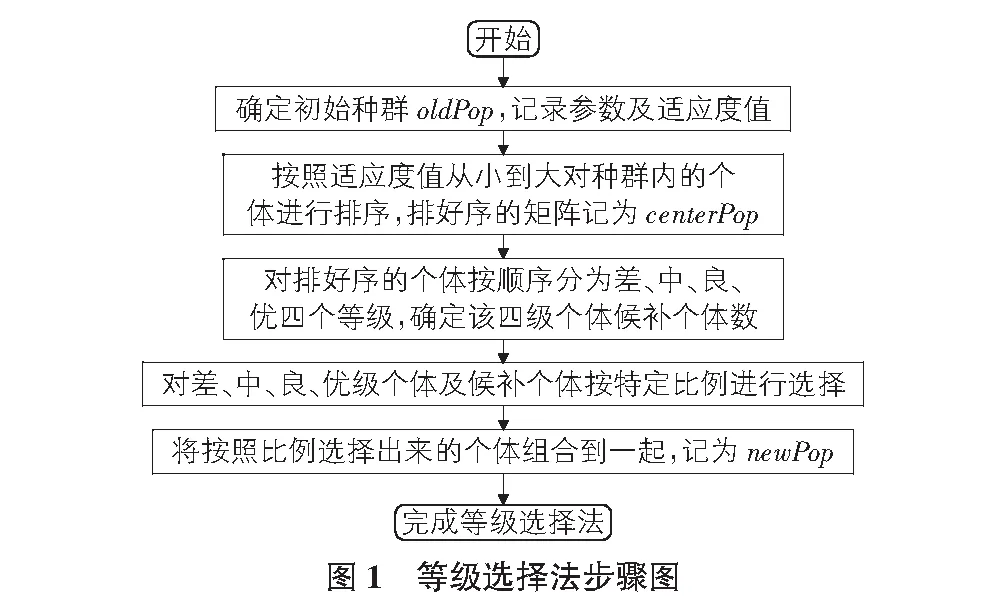
下面将“等级选择法”用图形表示。令种群数为20，P0=0.4，δ=0.2。用圆柱代表种群中的个体，圆柱中的数字代表适应度值，圆柱下的数字代表个体编号。

1)首先确定初始种群，种群数为20，见图2。

2)按照适应度值递增的顺序，将种群个体进行排序，见图3。

3)排好序的个体分为四个等级：差、中、良、优，见图4。

4)根据已确定参数，差、中、良、优四个等级的选择比例各自为0.4，0.6，0.8，1。为各个等级随机选择的个体数为：2，3，4，5，见图5。

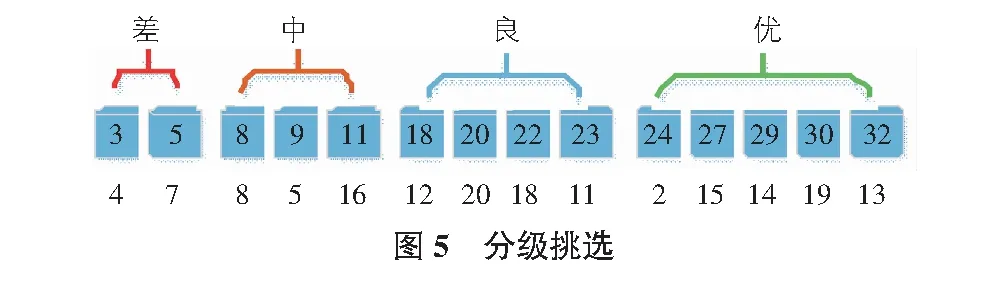
5)挑选出的个体，见图6。

6)因选择操作损失的个体数为：20-5-4-3-2=6，即候补个体数为6，其中包括5个优级个体和1个良级个体。候补个体见图7。

7)新种群=挑选出的个体+候补个体。将第5)步与第6)步的个体进行拼接，得到新种群，见图8。

新种群与初始种群相比，平均适应度明显提高。等级选择法既保证了选择优秀个体，又维持了种群选择多样性，使适应性较差的个体有机会被选中，提高了遗传算法的全局搜索能力。

3 改进遗传神经网络模型

3.1 改进遗传神经网络模型定义

单独使用BP神经网络模型容易陷入局部极值，效果不太理想[17-20]。利用等级选择法作为选择算子的遗传算法具有较强的全局搜索能力，用它来确定BP神经网络模型的权值和阈值，能得到更准确的预测结果。

把用“等级选择法”作为选择算子的遗传算法优化的神经网络模型称为“改进遗传神经网络模型”，把用经典“轮盘赌法”作为选择算子的遗传算法优化的神经网络模型称为“遗传神经网络模型”。

3.2 改进遗传神经网络模型实现

改进神经网络模型的流程如下：

Step 1将数据归一到[-1,1]；

Step 2确定神经网络的拓扑结构，进一步确定神经网络模型权值及阈值的个数；

Step 3对神经网络权值及阈值进行编码，得到初始种群；

Step 4进行解码，得到权值及阈值；

Step 5将解码得到的权值及阈值赋给新建的BP神经网络，得到误差值；

Step 6运用“等级选择法”进行选择；

Step 7进行交叉、变异运算，如果满足终止条件，则解码后得到最优的权值和阈值，否则回至Step 4。改进遗传神经网络模型实现流程见图9。

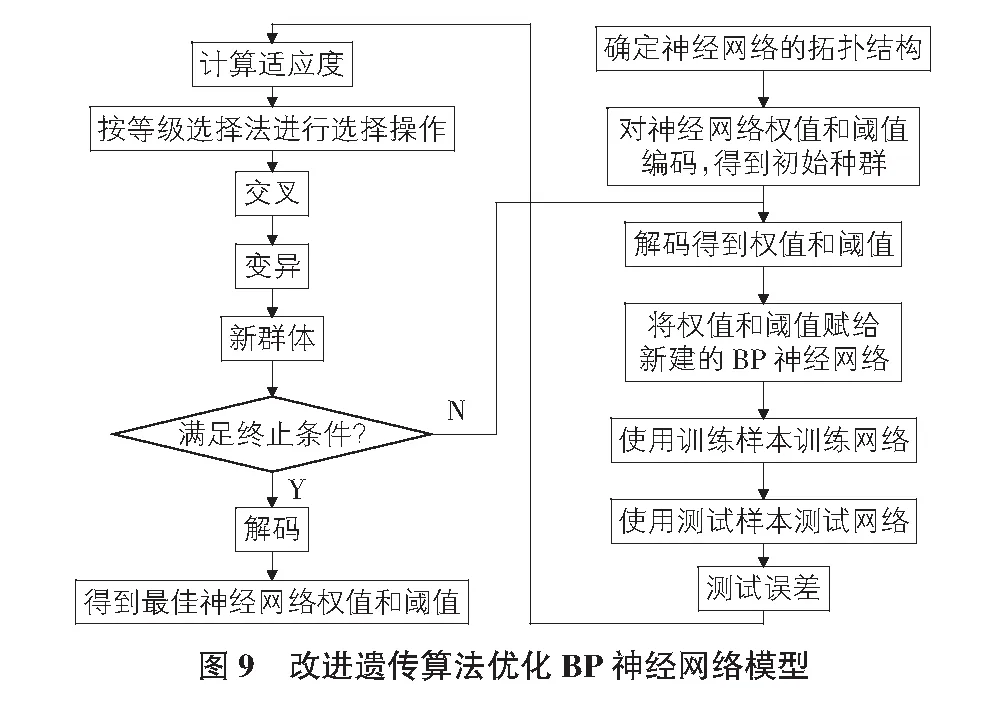
1)初始化种群。

基本遗传算法一般采用二进制编码，用0，1表示，使用较广泛，但其在基因中不能明确表达，而实数编码表达更具体，所以改进遗传算法采用实数编码。一个个体就是一串实数，包括输入层及隐含层之间的连接权值、隐含层阈值、隐含层及输出层之间的连接权值、输出层阈值。

利用经验公式法确定隐含层节点个数，如式(1)所示。

(1)

其中，l为隐含层节点个数；a为从1～10之间的常数；m为输入层节点数；n为输出层节点数。

改进遗传神经网络中待优化参数有Pb个，如式(2)所示。

Pb=m×n+n×l+l×n

(2)

激活函数采用双极S型函数，f(x)∈(-1,1)，x∈(-∞，∞)，表达式如式(3)所示。

(3)

2)适应度函数。

利用适应度函数筛选遗传算法的每代结果，模拟自然界优胜劣汰，选择优秀个体作为父代。适应度值是算法评价指标。对于计算结果，认为误差越小，其适应度值越大。令均方误差的倒数作为适应度函数，见式(4)。

(4)

其中，β为预测样本个数；yi为预测值；ti为真实值。

3)选择操作。

运用“等级选择法”进行选择操作，具体操作步骤在第2部分已详细介绍。

4)交叉操作。

交叉操作指选择出的个体按一定概率交叉得到新个体。改进遗传神经网络为实数编码，所以采用实数交叉，见式(5)。

(5)

其中，a为[0,1]之间的随机数；cmi为第m个染色体的第i位；cni为第n个染色体的第i位。

5)变异操作。

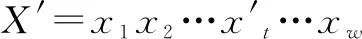
(6)

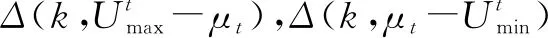
4 基于改进遗传神经网络模型的地表沉降预测

4.1 地表沉降监测数据

采用某市隧道施工某监测点连续63 d的数据进行地表沉降预测研究，沉降数据如图10所示。

4.2 基于改进遗传神经网络模型的地表沉降预测实现

运用地表沉降监测点过去5 d地表沉降量为时域特征输入，来预测未来一天的地表沉降情况，共构建58组数据。前80%的数据为训练样本，后20%的数据为预测样本。遗传算法参数如表1所示，BP神经网络模型参数如表2所示。

表1 遗传算法参数

表2 BP神经网络模型参数

在等级选择法中，按照P0,P0+δ,P0+2δ,P0+3δ的概率，分别给差、中、良、优四级个体进行分配。根据大量实验得出，当P0=0.4，δ=0.2时预测精度最高，此时四级个体的选择概率分别是0.4，0.6，0.8，1，对应初始个体数分别是12，12，13，13，选择出来的个体数分别是5，8，11，13。

将按比例选出的四级个体合并，共包含个体数n=37，需候补个体数为50-37=13。全部优级个体被选为候补个体。最后，将四级个体与候补个体进行拼接，完成遗传算法的一代选择操作。

4.3 预测结果及对比

分别采用BP神经网络模型、遗传神经网络模型、改进遗传神经网络模型对地表沉降值进行预测，预测结果见表3。

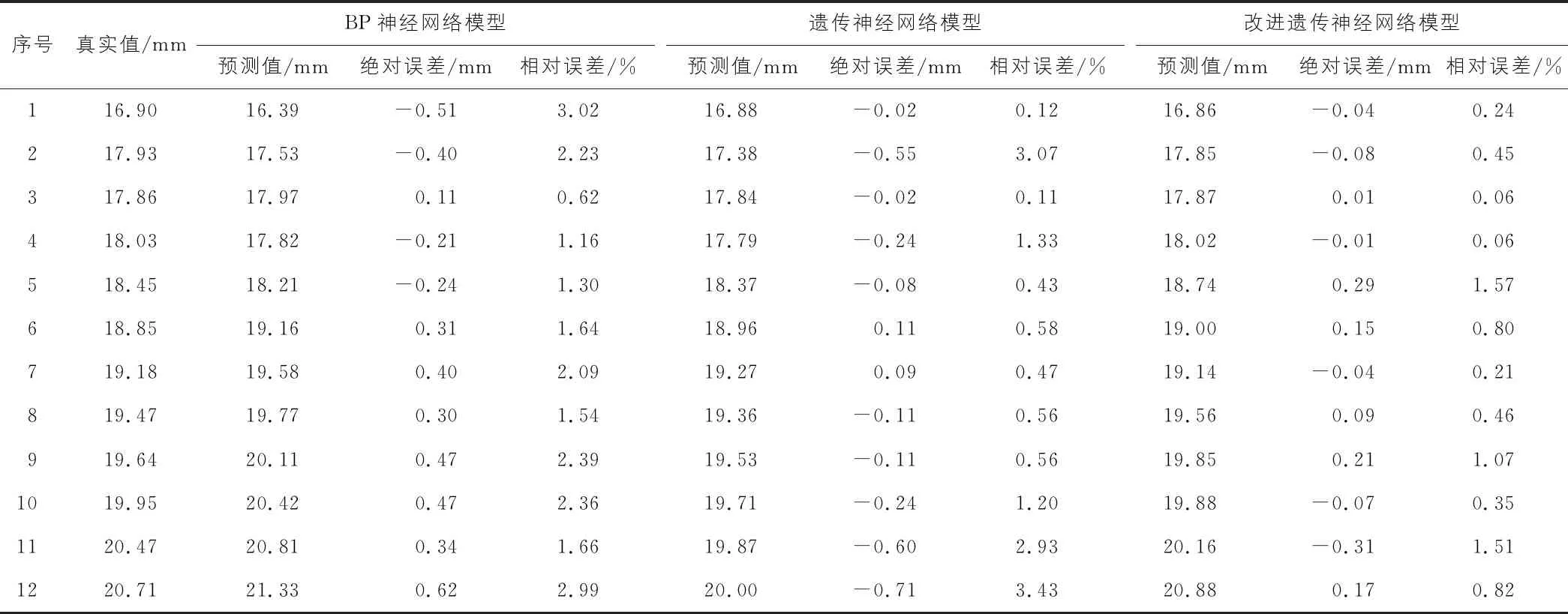
表3 三种神经网络模型预测值与真实值对比表

运用三种模型的地表沉降预测值如图11所示，预测绝对误差如图12所示。

对比三种模型预测结果的均方误差、计算时间。

均方误差的计算公式如式(7)所示。

(7)

其中，fi为预测值；ri为真实值；n为预测样本个数。mse值越小，模型的精度越高。

分别计算三种模型预测地表沉降时的均方误差，将三种神经网络模型分别独立运行50次，得到预测的均方误差平均值及平均运算时间如表4所示。

表4 三种神经网络模型结果对比

根据均方误差结果可知，遗传神经网络模型比BP神经网络模型均方误差平均值小0.024 484，预测精度高11.82%，改进遗传神经网络模型比遗传神经网络模型均方误差平均值小0.078 875，预测精度高43.18%，改进遗传神经网络模型比BP神经网络模型均方误差平均值小0.103 359，预测精度高49.89%，改进遗传神经网络模型的预测精度最高。根据平均运算时间分析，与BP神经网络模型相比，遗传神经网络模型、改进遗传神经网络模型运算所用平均运算时间更长，这是正常现象，因为遗传神经网络模型、改进遗传神经网络模型比BP神经网络模型增加了遗传算法的步骤。在进行地表沉降预测时，与遗传神经网络模型相比，改进遗传神经网络模型平均均方误差更小，平均运算时间更短，运算效率更高，证实了“等级选择法”的有效性。