基于AMEsim的带传动仿真模型的构建与分析

郑凯

(西安交通工程学院,电气工程学院， 陕西，西安 710300)

0 引言

随着现代工业技术及产业的快速发展，带传动系统作为工业生产与运输的主要设备被广泛应用[1]。带传动系统良好的静态、动态特性成为其安全、可靠、稳定运行的前提[2]。由于传送带的粘弹特性等原因，传统的刚体动力学分析[3-4]方法已经无法适应带传动系统的动态分析，故需要考虑构建一种新的带传动系统的仿真模型。本文在分析系统动力学原理的基础上，利用AMESim技术，分别搭建了理想弹性、理想粘性、理想粘弹三种带传动系统的仿真模型，并进行了相应的系统仿真。

1 设计目标

(1) 结合柔性多体系统动力学原理，分析理想弹性、理想粘性、理想粘弹三种模型，得到相关的动力学特性与关键指标。

(2) 利用AMESim技术，构建理想弹性、理想粘性、理想粘弹三种带传动系统的仿真模型，并进行系统仿真。

2 同步带传动系统的结构与工作原理

2.1 总体结构

同步带传动系统的结构，如图1所示。

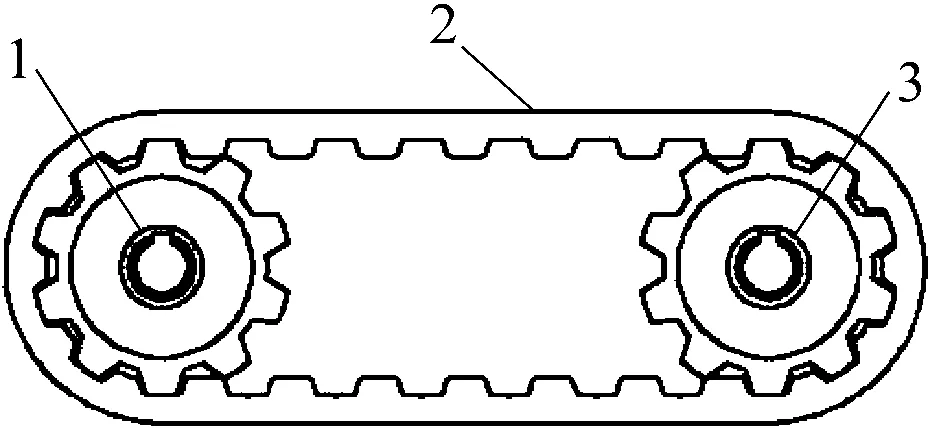
1—主动轮；2传送带；3—从动轮

2.2 工作原理与基本参数

如图1所示，由主动轮(1)、从动轮(3)和同步带(3)组成同步带传动系统。当主动轮(1)开始转动，主动轮(1)的轮齿槽与同步带(2)的带齿相啮合，通过相啮合的齿之间的相互挤压把圆周力传递给同步带(2)中的承载绳。承载将动力传递给从动轮(3)，进而带动从动轮(3)开始转动，完成主动轮(1)对从动轮(3)扭矩的传动。同步带传动系统的基本参数，如表1所示。

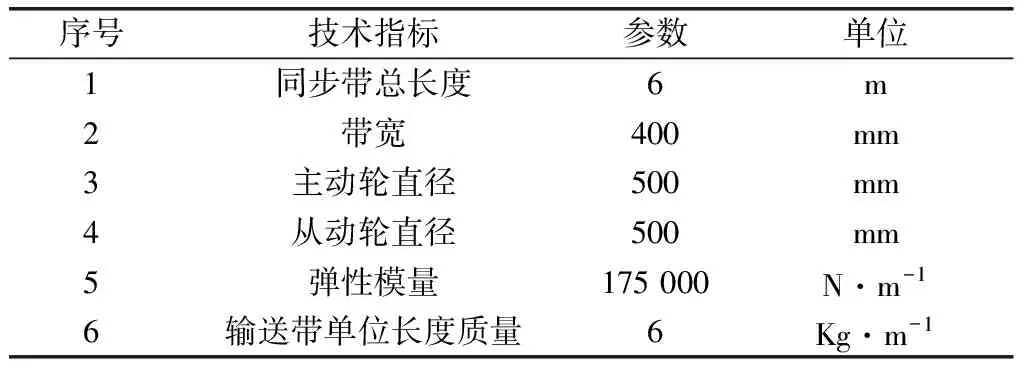
表1 同步带传动系统的基本参数

3 同步带传动系统的动力学分析

3.1 基本假设

本文将同步带传动系统作为连续体，采用偏微分方程的方式描述同步带传动系统的动力学行为[5-6]。为建立输送机数学模型，进行了如下假设。

(1)同步带横向振动影响较小忽略不计；(2)传送带剪切和弯曲应力忽略不计；(3)忽略传送带垂度变化引起的长度变化；(4)忽略传送带纵向拉伸引起的横向变形[7]。

3.2 动力学分析

3.2.1 理想弹性模型

将同步带传动系统看成理想弹性模型时，其应力表达式为

σ弹=Eε1

(1)

式中：E—弹性模量；ε1—应变

3.2.2 理想粘性模型

将同步带传动系统看成理想粘性模型时，其应力表达式为

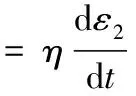
(2)

式中：η—粘滞系数；ε2—应变

3.2.3 理想粘弹模型

由公式(1)、(2)可知，若将同步带传动系统，看成理想弹性与理想粘性模型的组合时，其应力表达式为

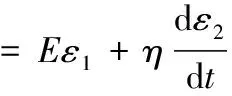
(3)

若ε=ε1=ε2；化简式(3)可得：

(4)

式中：E—弹性模量；ε—应变；η—粘滞系数

4 同步带传动系统的仿真模型

绘制系统草图。从AMEsim软件[8]的“Mechanical”机械库；选取相应的“元件”进行相应系统草图的绘制；建立子模型[9]。选择“首选子模型”赋予“元件”具体的物理特性。本系统所用“元件”均来自于AMEsim软件的标准库；设置参数。为各个“子模型”设置参数，就是为子模型中的系数赋予具体的“值”[10]；运行仿真。查看相应元件仿真结果，绘制动态曲线。

4.1 理想弹性模型

1.建立同步带理想弹性仿真模型，如图2所示。

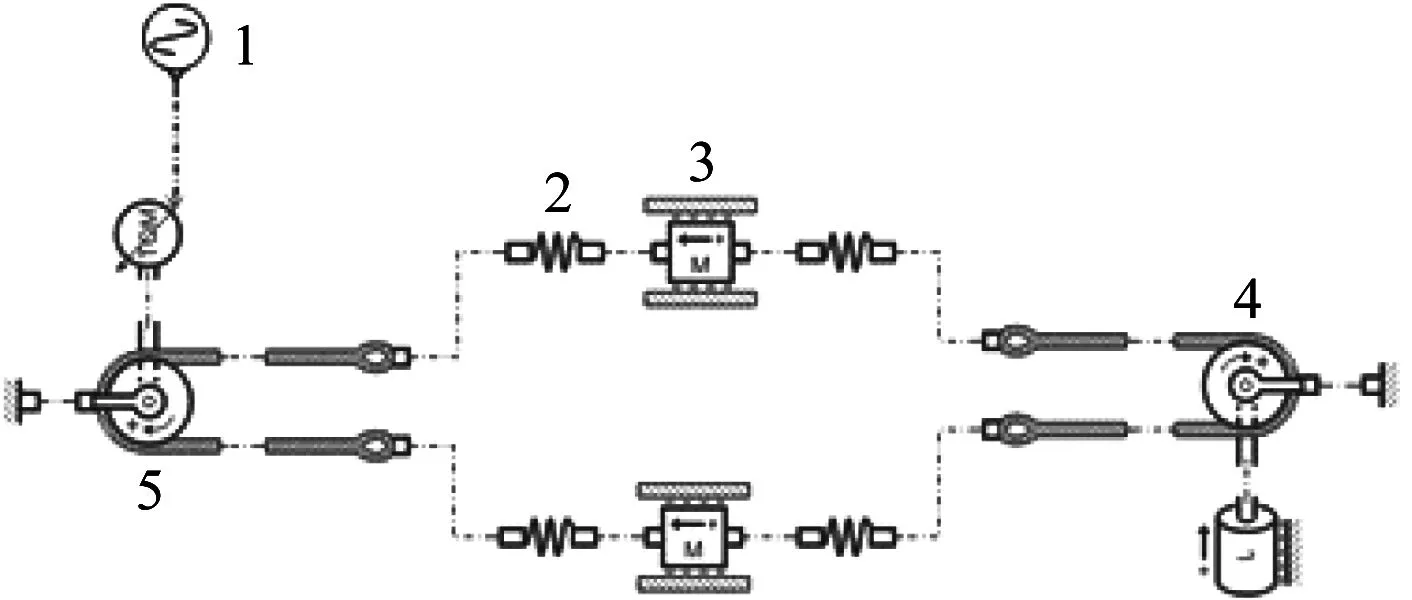
1—信号端，2—弹簧，3—质量块，5—从动轮，6—主动轮

2.设定子模型参数，如表2所示。

表2 理想弹性模型的子模型参数

4.2 理想粘性模型

1.建立同步带理想粘性仿真模型，如图3所示。

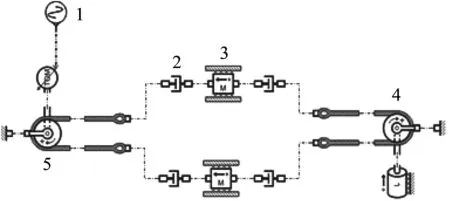
1—信号端，2—阻尼器，3—质量块，4—从动轮，5—主动轮

2.设定子模型参数，如表3所示。

表3 理想粘性模型的子模型参数

4.3 理想粘弹模型

1.建立同步带理想粘弹仿真模型，如图4所示。

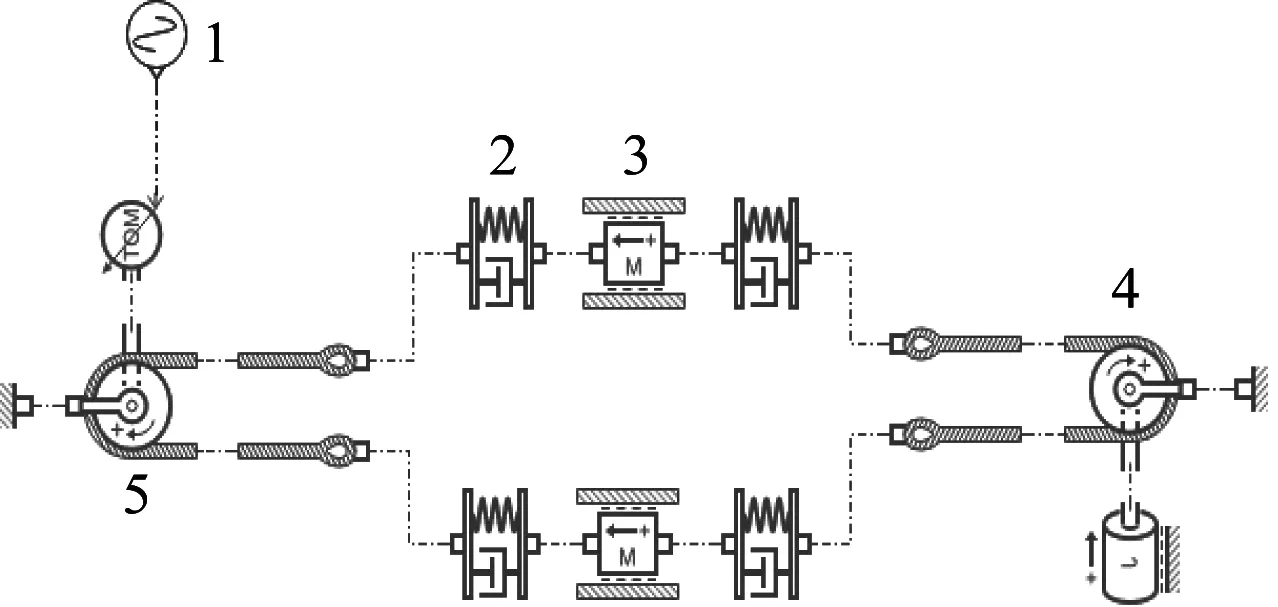
1—信号端，2—标准粘弹体，3—质量块，4—从动轮，5—主动轮

2.设定子模型参数，如表4所示。

文中运用AMEsim软件，通过绘制系统草图、建立子模型、参数设置进行了模型的构建。如图2、图3、图4所示，在模型的构建过程中，将同步带质量等效为质量块，通过设定质量块参数调整皮带的承载量。通过仿真模型的建立为后续的仿真分析提供了基础。

表4 理想粘弹模型的子模型参数

5 系统仿真与分析

本文对理想弹性模型、理想粘性模型、理想粘弹模型进行了仿真实验。

5.1 理想弹性模型的仿真

依据4.1中的仿真模型，按照表2中的参数进行设置并进行仿真，得到相应的特性曲线。如图5所示。

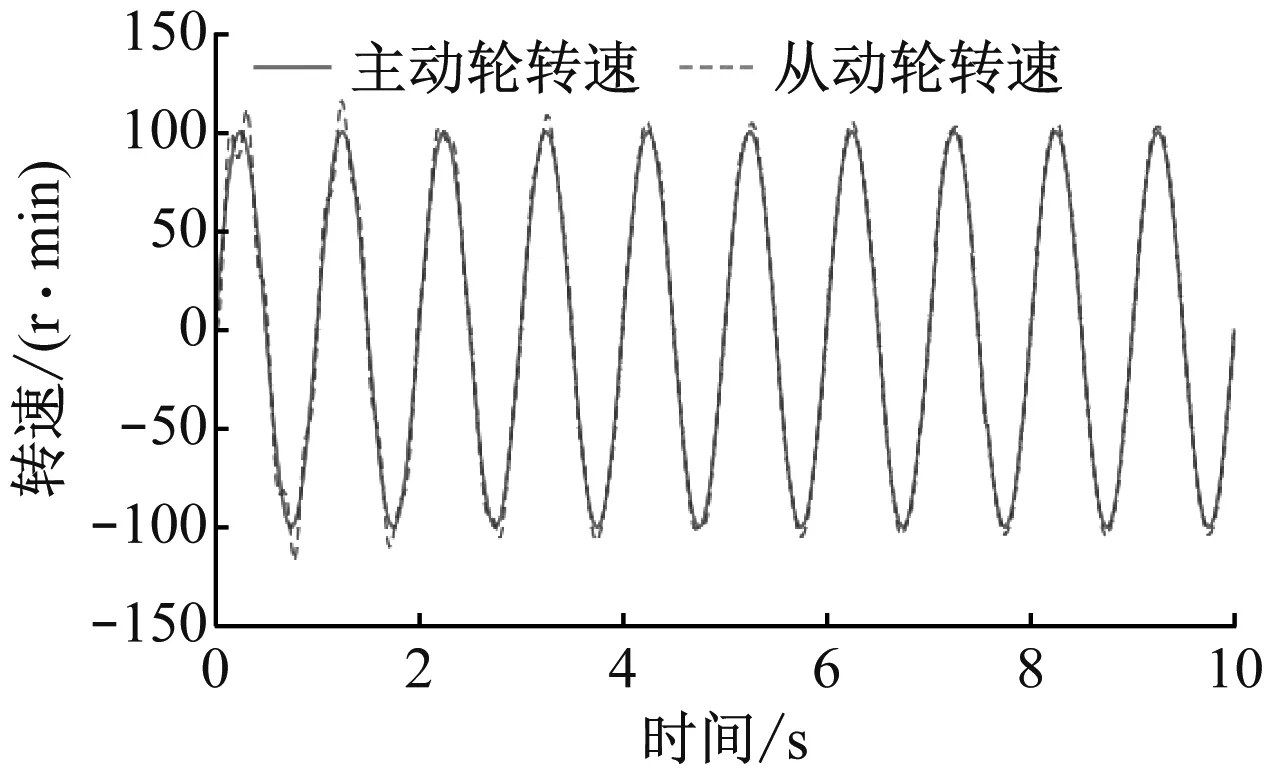
图5 理想弹性模型的特性曲线

如图5，若为理想弹性系统，弹性元件对传动力的吸收，使系统在开始阶段出现了一定的速度紊乱，因此无法准确反映整个同步带传动系统的运行情况。

5.2 理想粘性模型的仿真

依据4.2中的仿真模型，按照表3中的参数进行设置并进行仿真，得到相应的特性曲线。如图6所示。

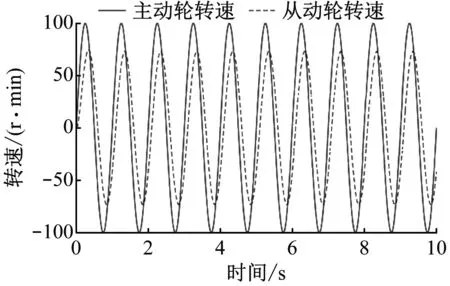
图6 理想粘性模型的特性曲线

如图6，若为理想粘性系统，传动时从动轮转速远小于主动轮，且从动轮在转动中出现了一定的延迟，因此无法准确反映整个同步带传动系统的运行情况。

5.3 理想粘弹模型的仿真

依据4.3中的仿真模型，按照表4中的参数进行设置并进行仿真，得到相应的特性曲线。如图7所示。

如图7，主动轮与从动轮传动速度同步且大小有明显的一致性趋势，较为准确的反映了同步带传动系统的运行情况。

6 系统仿真模型的优化与应用

由上文可知，将同步带传动系统看作理想弹粘模型时，较为准确的反映了同步带传动系统的运行情况。证明同步带是一种同时具有粘弹特性，且具有一定质量的连续体(本文将组成连续体的最小单元称为：单元模块)。

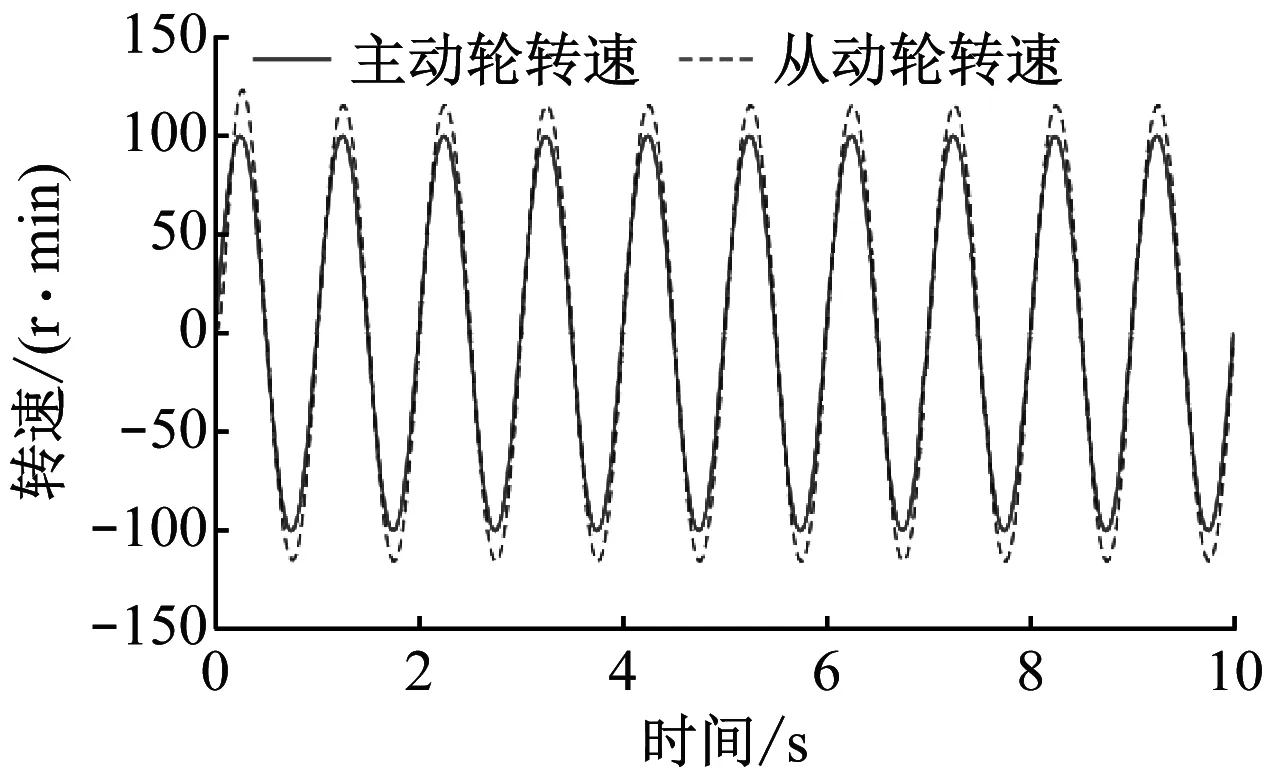
图7 理想粘弹模型的特性曲线

由于同步带具有一定的长度，因此在应用理想弹粘模型进行仿真时，可将同步带简化为有限个单元模块的串联。

1.建立同步带传动系统的优化模型

由表1可知，同步带总长度为6 m，既单边长度3 m。因此，本文图1中的同步带传动系统，其仿真模型可简化为6个单元模块的串联(单边3个)。如图8所示。

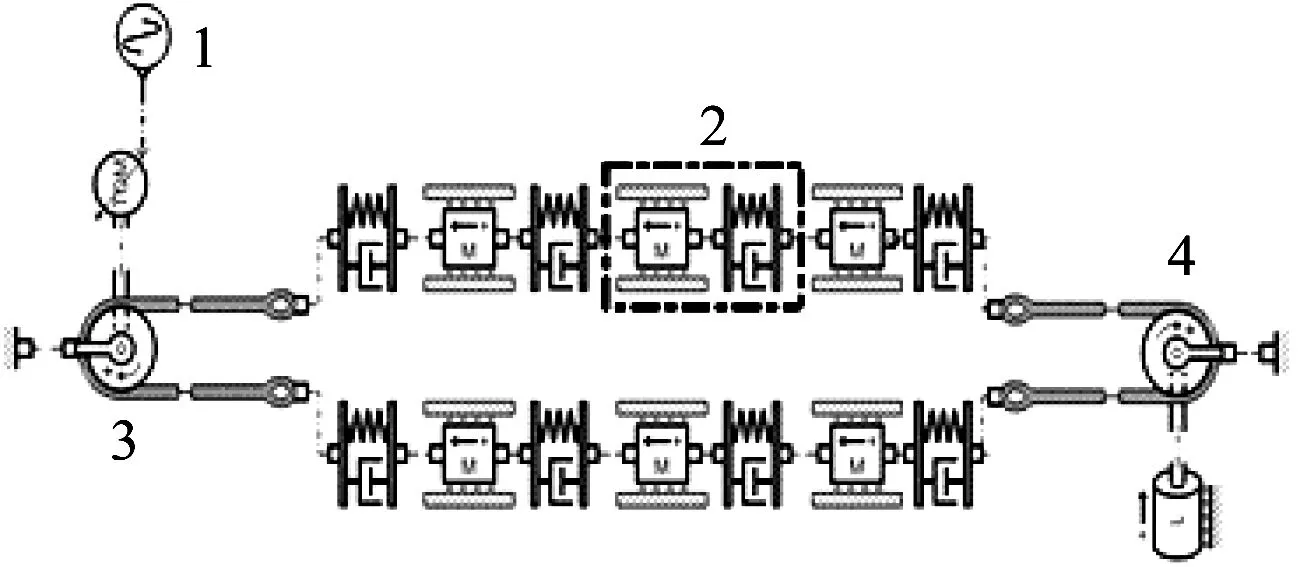
1—信号端;2—单元模块;3—主动轮;4—从动轮

2.设定子模型参数，如表5所示。

表5 优化模型的子模型参数

3.依据图8的优化模型，以及表5中的参数，进行了优化系统的仿真，其仿真结果如图9所示。

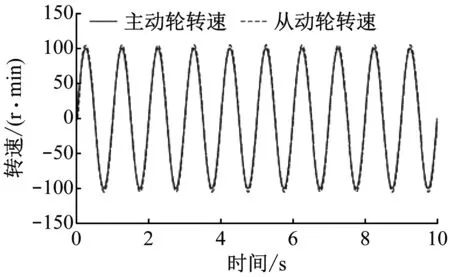
图9 优化模型的特性曲线

如图9的仿真结果可知，在对理想弹粘模型进行优化后，主动轮与从动轮传动速度之间的误差进一步的缩小，且主动轮与从动轮的传动过程明显一致。因此，将优化后的理想弹粘模型应用于同步带传动系统的仿真运算，能够准确的反映同步带传动系统的运行情况，具有实际的应用价值。

7 总结

首先，本文对同步带传动系统的结构、原理及动力学特性进行了分析，提出了理想弹性、理想粘性、理想粘弹三种模型。其次，利用AMESim分别搭建了理想弹性、理想粘性、理想粘弹模型并进行了系统仿真，证实了理想弹粘模型在同步带传动系统仿真中的可行性，同时对理想弹粘模型进行了优化。最后，利用AMESim搭建了优化模型并进行了仿真，发现主动轮与从动轮的传动过程变得明显一致，准确反映了同步带传动系统的运行情况，因此将本文构建与优化的仿真模型，应用于同步带传动系统的仿真运算，具有一定的应用价值。