基于自适应技术的教育类课程考试智能组卷方法

罗少华

(西安思源学院， 教育学院， 陕西， 西安 710038)

0 引言

在大数据管理日益成熟的条件下，通过计算机技术对教学题库进行深入的数据挖掘，自动生成高质量的考试试卷，对于辅助教学的研究具有重要意义[1-2]。当前教学领域中用于组织试卷内容的各种考试题目管理系统算法陈旧且随机性过强，严重影响了试卷的生成速度和知识考核质量[3-4]。为了解决这些问题，本文提出并设计一种经过优化的并行遗传算法，将自适应技术引入到遗传算法的种群迁移过程中，加快种群间优秀个体的迁移速度，进而实现高质量试卷的快速自动生成。仿真实验结果表明，优化后的并行遗传算法适应度更高、运行速度更快，对于智能组卷具有较强的实用性。

1 问题描述

1.1 约束指标

试卷内容的组织需要综合题量、考察知识点、考察题型、考试时间、区分度、难度系数、试卷总分、章节考察均衡等多种因素进行。试卷的内容必须满足几个方面的要求，包括出题频率、题目相关性、能力要求(记忆、运用、逻辑运算)、层次要求(熟悉、掌握、理解等)等。对于自动组卷的过程，组卷需求越多则效率会相应地降低。为了改善题库管理系统试卷生成模块的通用性和普适性进行了大量的同质分析，总结出试卷生成约束所涉及的几个指标如下:

(1)题目难度，即试卷题目对于参考人员的答题难易度，用于体现试卷的学习成果考察层次。

(2)区分度，用于对参考人员的学习水平进行区分，需要说明的是，区分度与试卷题目难度不成正比关系。

(3)试卷总分与考试时间。这两项指标是对考试的基本要求，用于体现得分标准与特定的答题时间需求。

(4)章节契合度，用于体现试卷整体上考察知识点分布的契合度。

1.2 目标矩阵

假定m为试卷中题目的数量，am1为单个题目分值，am2为单个题目难度系数，am3为区分度，am4为单个题目答题时间，am5为题目类型，am6为题目对应的知识点，则解空间中Dm×6的目标矩阵的表达式为

(1)

2 算法及其流程

2.1 算法机理

以粗粒度处理为前提的并行遗传算法依据处理器群的规模将原始种群分割成多个体形较大的子种群，单个处理器中的子种群独立开展遗传繁殖，在经历一定代数的进化过程后，各子种群间进行优良细胞的交换，从而实现子种群的并行遗传和共同进化。现有的研究结果表明，粗粒度并行遗传算法相较于其他算法在遗传结果方面具有较大优势。

本文所设计的粗粒度并行遗传算法的优点在于算法流程通畅且易于实现，其收敛性弱于传统遗传算法，最优解所在进化代数比传统遗传算法高，由此可以证明多子种群并行遗传能够实现种群的多样性，同时，该算法最优解方差较小，又说明了其稳定性高于传统遗传算法。粗粒度并行遗传算法在优化目标数量较多的情况下能够提供合理的参数设定方案，因此有较高概率在不增加计算步骤的基础上取得更好的运算结果。

通过本文所设计的算法处理多峰值模型时，需要在设定的进化代数按照一定比例完成子种群细胞迁移。在子种群进化的前半阶段中，子种群的组成细胞是被随机选定的，各子种群的适应度存在较大差异，只发生小规模的细胞迁移，因此，算法收敛以较慢的速度进行；而在子种群进化的后半阶段各子种群的适应度大多很快就会实现局部最优的状态，子种群适应度差异较小，且正在发生大规模、高频率的细胞迁移，很容易止步于局部最优解。由此可见，细胞迁移的规模和频率能够决定子种群间的数据交互量，是算法性能的决定因素。

运用统计学原理对子种群适应度差异进行量化统计，在运算过程中监测细胞迁移的频率和数量，能够在很大程度上加快并行遗传算法的收敛过程，同时绕过局部最优解，缩小数据交换带宽。

2.2 算法流程

子种群细胞迁移的过程中各子种群进行最优细胞互换，为了提升各子种群适应度差异的计算速度，筛选出各子种群的最优细胞，基于方差对子种群最优细胞的适应度差异进行计算，即

(2)

式中:Pi代表进化到第i代的子种群的适应度分布率，其数值范围为(0，1)，数值越大、离散度越高;fj代表经过i代进化后第j个子种群中最优细胞的适应度;fmax代表i代进化后种群中全部最优细胞的适应度;n代表子种群数量。

假定t为迁移阙值，在Pi≥t的条件下细胞开始迁移,则迁移细胞数量的自适应性表达式为

Ni=Pi(pN)

(3)

式中，Ni代表进化到第i代是发生细胞迁移的子种群数量，p代表假设的最高迁移率，N代表子种群细胞数量。

所设计的算法流程如图1所示。

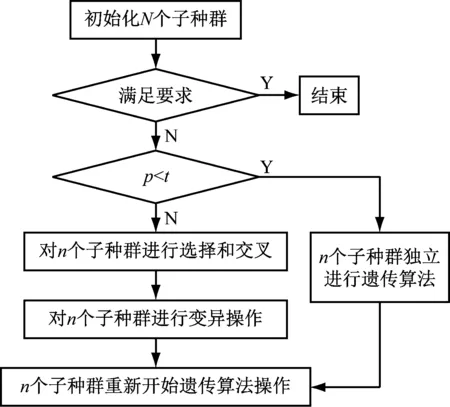
图1 算法流程

2.3 迁移拓扑

由于细胞的多样性特征，子种群间只交换基因最好的细胞，在这种条件下一对一的迁移模式能够加快收敛速度并提高解的精度，因此选取图2所示的环状拓扑迁移模型为研究对象。

图2 环状拓扑迁移模型

3 组卷算法设计及优化

3.1 编码策略

为了控制信息的长度，减轻通信载荷，细胞使用非固定长度实数进行编码，通过向量X=(x1,…,xm)T视为单个细胞用于代表一个解。在细胞内部依据题目类型分段进行编码。

3.2 种群初始化

在系统搜索的开始阶段，为了保证子种群的差异化，其初始化以随机的方法进行。设定组卷过程中子种群的数量为n，利用随机函数在符合条件的题目中随机选取m个来构建单个细胞。

3.3 调用适应度函数

适应度值能够体现细胞的优劣，值越大、细胞基因越好。适应度函数大多由目标函数转换而来，能够决定算法的性能。

以SVM(支持向量机)为理论基础在线性可分的条件下开展分析，在出现线性不可分的情况时，需要基于非线性映射函数把处于低维度空间的不可分样本映射至高维度特征空间，使其具有线性可分的性质，进行实现线性可分的普适性。

适应度函数f通过SVM原理来检测细胞与迁移目标种群的距离，距离最小者为最佳迁移目标。考虑到约束指标在组卷过程中存在重要性的差异，因此需要评定每一个约束指标的优先级，优先级越高，题目选取时所占权重越大。

f=η/F

(4)

式中，η代表惩罚因子，F代表细胞评估函数。经过k+1代进化后惩罚因子的表达式为

(5)

式中，fkmax代表最大适应度值，fki代表经过k代进化后第i个细胞的适应度，n代表子种群细胞数量。

(6)

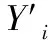
3.4 遗传算子

(1)算子选取

在研究的过程中基于精英保留策略来保证种群进化的行效率，优良细胞直接进入下一代进化，其余细胞通过转轮赌的方式进行选取。种群中当个细胞被选中的概率为

(7)

式中，Fit(i)代表第i个细胞的适应度，popsize代表种群体形大小。当任意细胞的选择概率计算完成时，系统会自动随机生成一个取值区间为(0，1)的数组，用数组的值与细胞选择概率值进行对比，若前者大于后者，则该细胞被选取并进入下一代进化，否则将被剔除。

(2)交叉算子

本文基于单点交叉法对算法进行完善。具体过程为：在细胞序列中随机选定一处交叉点，进行交叉操作，互换交叉点前后细胞的部分结构，进而创建2个新的细胞。

(3)变异算子

基于基本变异法进行算法的简化，具体做法是在完成细胞的实数编码后，从编码串中随机选中一个或多个编码并改变其数值。

3.5 遗传的自适应设计

通过自适应遗传算法可以同时保证子种群的收敛性与多样性。改变交叉、变异的概率会对细胞的适应度产生较大影响，在适应度数值向局部最优或整体一致的方向变化时，应增大交叉与变异的概率；而当适应度差异较大时，则应减小对应的概率值。那些适应度数值比整体平均值大的细胞都应作降概率处理并延续到下一代进化过程，其余低于平均值的细胞将会被从种群中移除。因此必须对交叉和变异的概率进行精确计算，才能保证算法的整体适应性处于较高水平。

(1)交叉概率计算

交叉概率Pc的计算式为

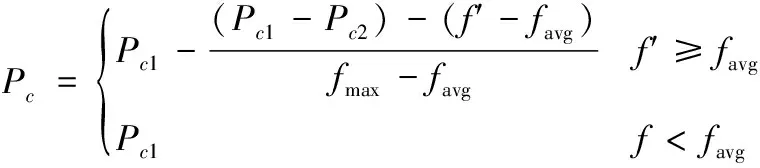
(8)

式中，Pc1和Pc2分别取0.9和0.6，f代表当前细胞的自适应度，favg代表种群所有细胞的平均自适应度。

(2)变异概率计算

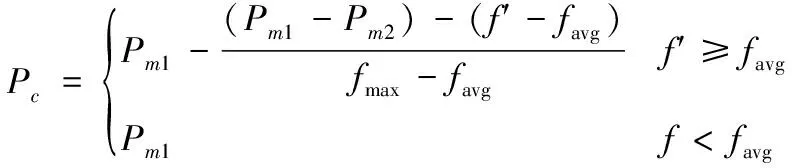
(9)

式中，Pm1和Pm2分别取0.1和0.001，f代表当前细胞的自适应度，favg代表种群所有细胞的平均自适应度。

3.6 算法终止条件

在出现以下3种情况的条件下终止算法的运行：

(1)已经发生的遗传代数超过限定代数值；

(2)最优细胞与目标细胞的差值已经小于阈值；

(3)当前遗传代的最优细胞与上一代最优细胞的差值已经小于阈值。

4 应用验证

通过自动组卷实验对本文所设计的与传统PGA算法[5]进行性能对比，以验证本文所设计算法的应用效果。

实验从计算机专业“数据库原理”(王珊，清华大学出版社，2018)一书的练习题库中选择题目进行自动组卷，该题库共包含10 521道题目，其章节题量、知识点考察、题目难度分布较为均匀。

试卷约束指标参数设定为试卷总分值100分，答题时间120 min，难度系数为0.3，区分度为0.5，章节题目契合度为0.8。种群初始体形大小为50，数量为24个，限定最高遗传代数为100。

分别基于2种算法完成自动组卷实验，每种算法重复200次，算法的收敛速率通过100次遗传的平均耗时进行计算，通过本文算法所生成的“数据库原理”试卷如图3所示。实验结束后对比2种算法的遗传收敛速率及种群适应度。

经过对比，本文算法100代迭代平均耗时14.62 s，传统PGA算法100代迭代平均耗时18.72 s。收敛速度对比如图4所示。由此可见，本文所设计的算法在最优适应度和遗传效率2个方面都比传统PGA算法更具优势，且随着遗传代数的增多其优势也随之持续扩大。应用本文算法的考试题目管理系统已在多所院校投入使用，师生们普遍反映该系统所生成的各科试卷知识点覆盖面广，章节分布均匀且难易程度适中，能够科学地考查学生们对所学课程的掌握情况，因此给予一致好评。

图3 基于本文算法所生成的“数据库原理”试卷

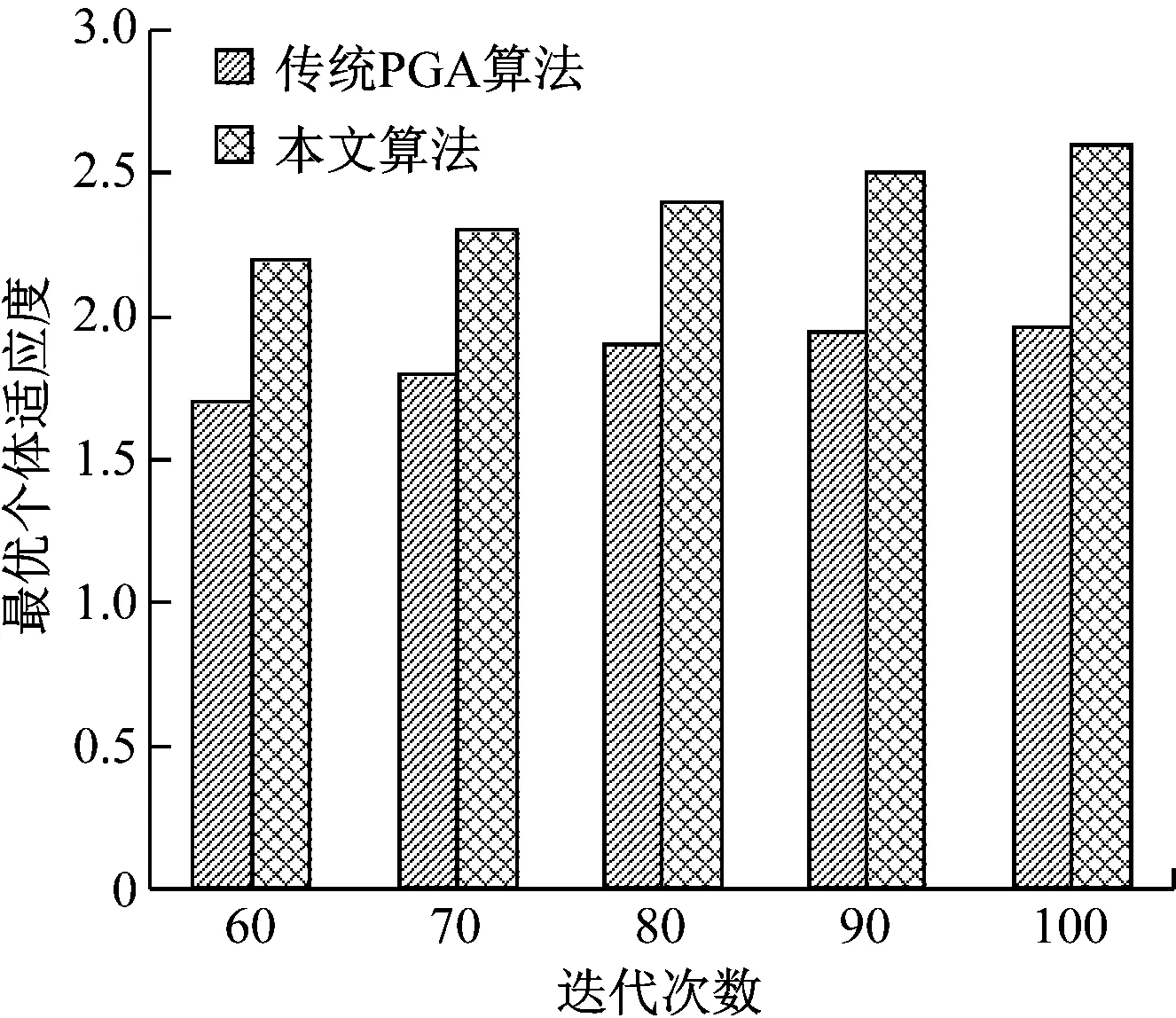
图4 PGA与HPAGA收敛速度对比结果

5 总结

传统的遗传算法在自动组卷过程中普遍存在执行效率低下、试卷质量难以保证的问题，为此，本文基于自适应技术对并行遗传算法进行了优化，介绍了算法优化机理及实现流程，阐述了算法的设计过程和优化方式，并通过实验证明了本文所设计的算法相较于传统算法在算法性能和执行效率上均具有明显的优势。基于自适应技术的并行遗传算法实现了种群迁移的高效性和和遗传效果的显著性，能够通过自动组卷技术的改进对辅助教学的研究起到良好的促进作用。