跳-扩散市场环境下基于股票误定价的DC型养老金最优投资策略
2022-05-11殷艳红夏登峰郭宇超
殷艳红,夏登峰,郭宇超
(安徽工程大学 数理与金融学院,安徽 芜湖 241000)
养老金管理关乎国家安全稳定与民生福祉,最优资产配置将有效提升养老金账户收益。养老金分为确定收益型(Defined Benefit,DB)和确定缴费型(Defined Contribution,DC)。本文讨论DC型养老金以其效用最大化为目标,从而找到一种最优投资策略以获取最大收益。
养老金的最优资产投资策略问题近年来引起了人们的广泛关注,研究工作较多。因养老金投资时间长、跨度大,管理者需要充分考虑市场风险带来的影响,比如利率风险、波动风险以及通胀风险。Deelstra等[1]在保证终端财富最大值的情况下研究养老金最优投资策略问题时假设利率是随机的。Chen等[2]研究了通胀环境下具有损失厌恶并提供最低保障的保险公司的最优资产配置问题。Wang等[3]研究了DC型养老金计划成员的鲁棒最优投资组合选择问题。乾丞健等[4]在Heston模型下研究了具有违约风险的DC型养老金计划的均衡投资策略。Tang等[5]在研究养老金的最优资产配置时综合考虑了随机利率、通胀和最低保障。
以上研究中风险资产的价格过程是连续情形,但在实际金融市场中,风险资产的价格可能会出现跳跃情况。付渴等[6]假设风险资产价格满足跳-扩散模型,在均值-方差下研究了养老金时间一致最优投资策略的问题。费为银等[7]在跳-扩散环境下研究了带通胀的最优动态资产配置问题。龚晓琴等[8]在随机利率和随机波动率下假设风险资产满足跳-扩散模型,研究了保险和再保险公司的稳健投资策略。Li等[9]在均值-方差框架下考虑了具有跳-扩散风险不确定性的DC型养老金计划的α稳健最优投资问题。还有文献[10-11]均假设盈余过程满足跳-扩散模型,研究了保险公司的最优超额再保险和投资策略问题。
股票误定价是指股票估计价值与真实价值之间存在的差值或同一只股票在不同市场上的价值差值,包括股票价格被低估和被高估的偏差。Wang等[12]在研究政府和保险公司的稳健最优保险和投资策略中假设保险公司可投资于带有误定价的股票。Winston等[13]研究了信息不对称下股票的误定价模型。Ma等[14]在Heston模型下研究了带有误定价的DC型养老金计划的最优投资策略问题。
本文假设养老金管理者将保费分别投资于无风险资产和带有误定价的风险资产股票,并假设其中一个的价格过程是跳-扩散的,研究了管理者的终端财富效应最大化问题。通过求解关于养老金管理者值函数满足的HJB方程,得到其最优投资策略,并通过数值模拟,从经济学角度分析了各参数对养老金管理者最优投资策略的影响;推广了已有结果,对养老保险市场具有一定的指导意义。
1 模型设定
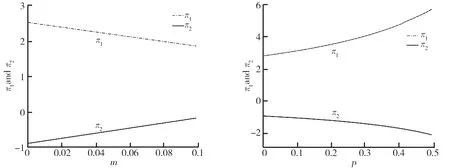
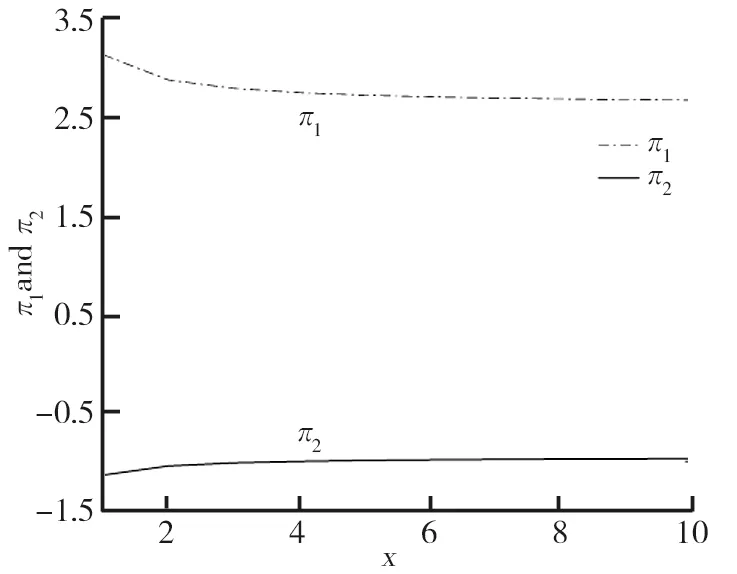
W(t)=(Wp(t),Z(t),Z1(t),Z2(t))是定义在完备带流概率空间(Ω,F,{Ft}t∈[0,T],P)上的标准布朗运动。信息流Ft=σ{W(s);0 假设无风险资产的价格过程S0(t): (1) 式中,r>0为无风险利率。 类似文献[14]中,S1(t)、S2(t)表示同一种股票在两个不同市场中的价格过程,且S1(t)满足跳-扩散模型,满足 (2) 且α1、α2是正常数,l1、l2、a、b是常数,l1、l2是控制均值回归率的参数,Wp(t)、Z(t)、Z1(t)、Z2(t)是标准布朗运动,且相互独立。adZ(t)表示股票相同风险,bdZi(t)表示股票个体风险。 类似文献[8]中: 此时,S1(t)股票价格过程则可以表示为 (3) 根据伊藤引理,价格误差动态过程M(t)可表示如下: 本文假设工资是关于时间t的确定性函数P(t),投保人按工资的固定比例ε缴纳保费直至退休。在DC型养老金的积累期[0,T],管理者可以将保费投资于不同金融市场中的风险资产,假设在t时刻投资于风险资产S1(t)、S2(t)的比例分别为π1(t)、π2(t),则投资于无风险资产为1-π1(t)-π2(t)。投资者的财富过程为X(t),满足如下方程: (4) 将式(1)~(3)代入式(4),可得 (5) 首先利用随机最优控制推导优化问题的一般框架,然后找出期望效用函数的最优策略。养老金管理者的目标是终端财富期望效用最大化,即 maxE[U(X(T))]。 假设养老金管理者有一个恒定的相对风险厌恶(CRRA),并遵循如下效用函数: p是相对风险厌恶系数。采用随机最优控制方法,定义管理者的值函数为 ∏表示允许的投资策略集。 算子Aπ满足如下式子: AπH(t,x,m)=Ht+Hx·x[-m(l1π1(t)-l2π2(t))+((α1+ap)π1(t)+α2π2(t))+r]+ 式中,H(t,x,m)∈C1,2,2([0,T]×R×R),H满足以下的HJB方程: (6) 边界条件H(T,x,m)=U(x)。 由式(6)最优性一阶条件可得 (7) 其中, 为求解HJB方程,猜测 (8) 综上可得如下命题。 其中, 当u1>0时, 当u1<0时, 证明见附录A。 本节通过数值模拟说明误定价系数和其他参数对最优策略的影响。假设m>0,l2-l1>0,这意味着股票S1的定价相对于真实价值来说被高估了,S2价值被低估了,且被低估的股票S2回归均值的速度要快于被高估股票S1回归均值的速度。 相关参数设定如表1所示。β(t)为时间t的确定性函数,为了方便分析,以下假设β(t)和P(t)为常数,分别设β(t)=1,P(t)=0.5。 表1 相关参数设定 误定价系数描绘了股票的价差,p=0.1时,m对π1(t)、π2(t)的影响如图1所示。由图1可见,随着m的增大,π1(t)逐渐减小,π2(t)逐渐增大。当定价偏离程度增大时,养老金管理者担心股票S1价格虚高会骤跌,为了规避损失减少买进被高估的股票S1;同时也减少卖空定价偏低的股票S2,以获取更大的利润。 图1 p=0.1时,m对π1(t)、π2(t)的影响图2 m=0.1时,p对π1(t)、π2(t)的影响 m=0.1时,p对π1(t)、π2(t)的影响如图2所示。由图2可见,当股票价差一定时,随着管理者对风险的厌恶程度增大,管理者购买更多被高估的股票S1,同时抛售定价偏低的股票S2,以获得更大的利润。 m=0.1,p=0.1时,x对π1(t)、π2(t)的影响如图3所示。由图3可见,π1(t)随着x的增大呈现小幅度的减少,π2(t)随着x的增大呈现小幅度的增加。因为养老金缴费时间长、跨度大,所以初始财富的多少对投资策略的影响不大。 图3 m=0.1,p=0.1时,x对π1(t)、π2(t)的影响 本文研究了在跳-扩散市场环境中,带误定价的DC型养老金的最优投资策略问题。首先考虑跳-扩散模型下,将保费投资于带误定价的风险资产和无风险资产,利用最优控制理论解相应的HJB方程得到养老金管理者的最优投资策略。通过数值分析,模型参数对投资策略的影响符合市场交际,具有一定的经济意义。本文假设无风险资产的利率为常数,接下来将考虑通货膨胀的影响,假设利率是随机形式,考虑到投保人提前死亡还可以加入保费退还,使模型更贴近实际市场。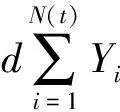
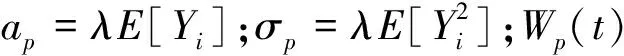
2 最优投资策略
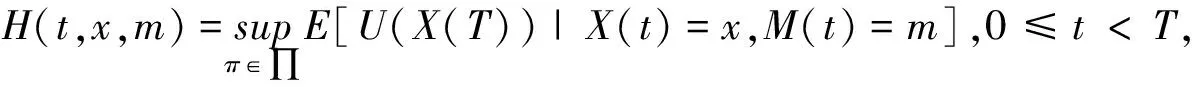
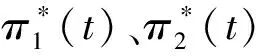
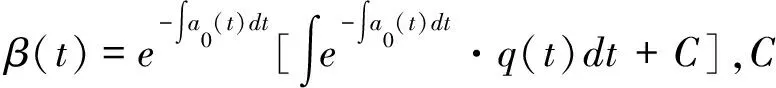
3 数值分析

3.1 误定价系数m敏感性分析
3.2 风险厌恶系数p敏感性分析
3.3 初始财富x敏感性分析
4 小结
